こんにちは!
デジタルマーケター兼データサイエンティストのウマたん(@statistics1012)です!
データの傾向・性質を見る指標はたくさんありますが、「データの散らばり具合を見る」指標である分散は非常に重要です!
具体的には「データが平均からどれだけ散らばっているか」示しており、データのばらつきが大きいと分散が大きくなり、ばらつきが小さくなると分散は0に近づく特徴を持っています!
この記事では、そんな分散の解説をしながらも分散の性質を持つ標本分散と不偏分散の違いについて解説していきます。
・分散の定義について
・標本分散・不偏分散の違いについて
・Pythonで分散を実装!!
以下の動画でも解説していますのであわせてチェックしてみてください!
分散とは?

分散とは「データのばらつきを示す指標」と定義されています。分散の値が分かることで、データの分布が予想でき、データの比較が行うことができます!
\(s^{2}\) = \(\frac{1}{n}\)\(\sum_{i=1}^{n}\) \((x_i – \bar{ x })^{2}\)
これらの式では、\(n\)がサンプルサイズ,\(x_i\)が各サンプルごとの値、\(\bar{ x }\)が平均値を表しています!特に\((x_i – \bar{ x })\)を偏差と呼びます!
標本分散とは?
分散の定義を説明したので、標本分散の説明をしていきます!
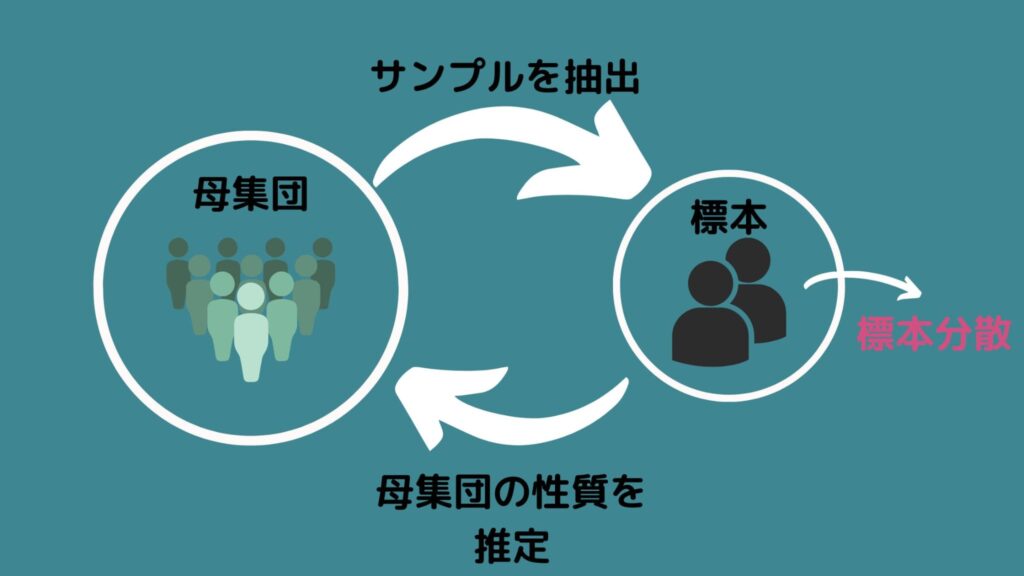
標本分散とは、「標本から計算した分散」を示しています。つまり対象の全体から一部を抽出したデータの分散を意味しています!

\(s^{2}\) = \(\frac{1}{n}\)\(\sum_{i=1}^{n}\) \((x_i – \bar{ x })^{2}\)
不偏分散とは?

次は不偏分散の説明です!
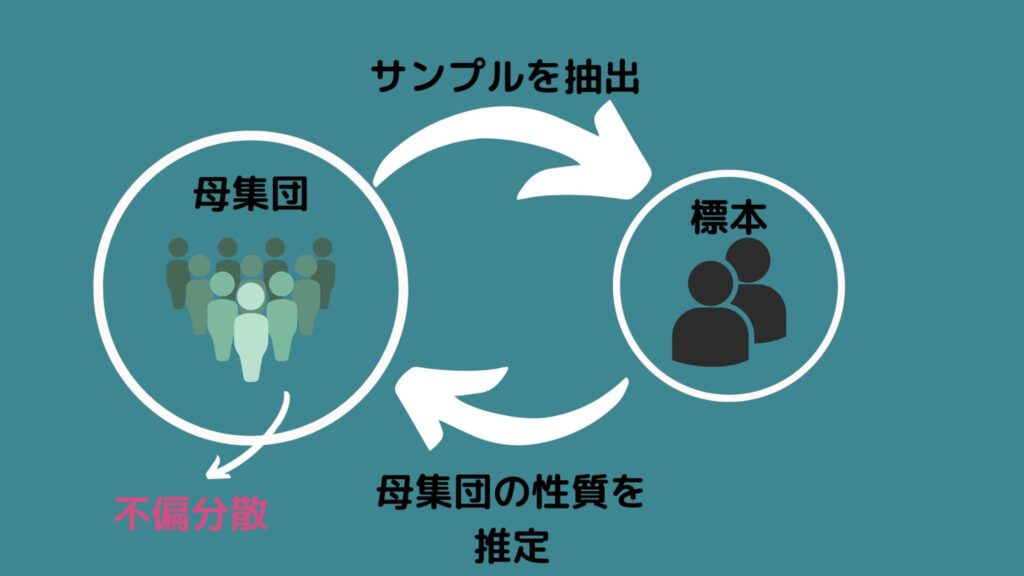
不偏分散とは、「標本が属する母集団の分散を推定した値」を示しています!

\(s^{2}\) = \(\frac{1}{n-1}\)\(\sum_{i=1}^{n}\) \((x_i – \bar{ x })^{2}\)
標本分散は不偏性を持つのか?


\(E\)(\(\hat\theta\)) = \(\theta\)
\(\hat\theta\)を推定量、\(\theta\)を母数とすると、「あるパラメータの推定量の期待値は母集団のパラメータに等しい」ということを言っています!標本から母集団のパラメータを良く推定できる強みがありますね。
そして標本分散を\(\hat\theta\)に代入してみましょう!
\(E\)(\(s^{2}\)) = \(E\)(\(\frac{1}{n}\)\(\sum_{i=1}^{n}\) \((x_i – \bar{ x })^{2}\)) = \(\frac{1}{n}\)\(E(\sum_{i=1}^{n} ((x_i – \hat{μ} ) – (\bar{ x } – \hat{μ} ))^{2}\))
= \(\frac{1}{n}\)\(E(\sum_{i=1}^{n} ((x_i – \hat{μ})^{2} – 2\sum_{i=1}^{n}(x_i – \hat{μ})(\bar{ x } – \hat{μ}) + \sum_{i=1}^{n}(\bar{ x } – \hat{μ} )^{2})\)
= \(\frac{1}{n}\)\(E(\sum_{i=1}^{n} ((x_i – \hat{μ})^{2} – 2n(\bar{ x } – \hat{μ})^{2} + n(\bar{ x } – \hat{μ})^{2}))\)
= \(\frac{1}{n}\)\(E(\sum_{i=1}^{n} ((x_i – \hat{μ})^{2} – n(\bar{ x } – \hat{μ})^{2})))\)
= \(\frac{1}{n}\)\(E(\sum_{i=1}^{n} (x_i – \hat{μ})^{2}) – E((\bar{ x } – \hat{μ})^{2})\)
= \(\frac{1}{n}\)\((n\)\(\sigma^{2})\) – \(\frac{\sigma^2}{n}\)
= \(\frac{n-1}{n}\)\(\sigma^{2}\) (*\(V(x_i)\) = \(E((x_i – μ)^{2})\)、\(V(\hat{x})\) = \(E((\hat{x} – μ)^{2})\)とする)
\(E(s^{2})\) ≠ \(\sigma^{2}\)なので標本分散の期待値は母分散と一致しない、つまり標本分散は不偏性を持たないことになります!
またさっきの式から、不偏分散は不偏性を持つこともわかりますね。
\(E(\frac{n}{n-1}\hat{\sigma}^{2})\) = \(E(\frac{n}{n-1} \frac{1}{n}\sum_{i=1}^{n} (x_i – \bar{ x })^{2})\) = \(E(\frac{1}{n-1}\sum_{i=1}^{n} (x_i – \bar{ x })^{2})\) = \(\sigma^{2}\)
実際に標本分散・不偏分散をPythonで計算してみよう!


最後にPythonで標本分散・不偏分散を実装しましょう!
標本分散・不偏分散はNumpyライブラリのvar関数で算出することができます!特にvar関数はddof=Trueとすると不偏分散を算出してくれます。
問題の設定として、架空の学校にあるA組とB組のテストの平均と標本分散・不偏分散を見ることにしましょう。サンプルサイズは10人とします。
import numpy as np
#A組・B組のデータ
A = np.array([50,60,57,63,55,65,51,69,49,71])
B = np.array([30,80,40,90,25,95,32,88,27,93])
#結果
print("A組の平均:"+str(np.mean(A)))
print("B組の平均:"+str(np.mean(B)))
print("A組の標本分散:"+str(np.var(A)))
print("B組の標本分散:"+str(np.var(B)))
print("A組の不偏分散:"+str(np.var(A,ddof=True)))
print("B組の標本分散:"+str(np.var(A,ddof=True)))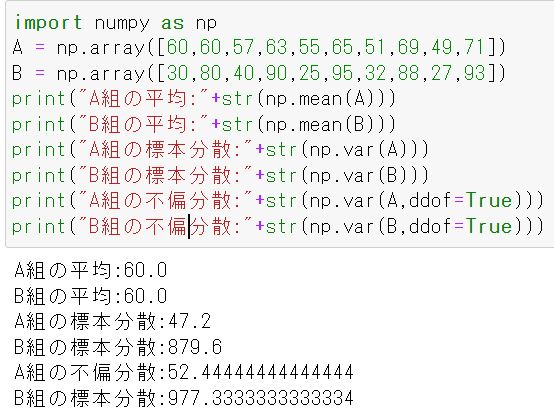
A組・B組の点数の平均は同じですが,分散に関してはB組の方が圧倒的に大きいことが分かります。つまりB組の点数のばらつきが大きいことを意味してますね!
またddof=Trueにすることでキチンと不偏分散を算出してくれていることも確認できました!
不偏分散と標本分散 まとめ


本記事では、分散の定義と標本分散・不偏分散の違いについてまとめました!
データの性質・傾向を見るために、データのばらつきを表す分散は非常に重要な指標でした。さらに分散だけでなく平均値を見たり、ヒストグラムからデータの分布を見る癖をつけると、データに対する理解が深まること間違いなしでしょう!
そうしたデータサイエンスの力を身に付けるためにはスタビジの記事やスクールを活用すると良いでしょう。
そして僕の経験を詰め込んだデータサイエンス特化のスクール「スタアカ(スタビジアカデミー)」を運営していますので,興味のある方はぜひチェックしてみてください!
AIデータサイエンス特化スクール「スタアカ」


| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています!
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
データサイエンスに関する記事はこちら!


データサイエンスを勉強できるスクールやサイトは、ぜひこちらを参考にしてみてください!

























