Bipiramidă alungită

Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici.

Bipiramidă alungită
Exemplu: bipiramidă hexagonală alungită
Descriere
Fețe	2n-triunghiuri, n pătrate
Laturi (muchii)	5n
Vârfuri	2n + 2
χ	2
Grup de simetrie	Dnh, [n,2], (*n22)
Grup de rotație	Dn, [n,2]+, (n22)
Poliedru dual	bitrunchi
Proprietăți	convexă

În geometrie, bipiramida alungită este un poliedru convex, construit prin alungirea unei bipiramide n-gonale prin inserarea unei prisme n-gonale între bazele piramidelor (bazele prismei și ale piramidelor trebuie să fie congruente).

Numărul bipiramidelor alungite este infinit, dar dintre ele trei sunt poliedre Johnson: bipiramida triunghiulară alungită (J₁₄), bipiramida pătrată alungită (J₁₅) și bipiramida pentagonală alungită (J₁₆). Bipiramide alungite cu n mai mari pot fi construite cu triunghiuri isoscele.

Poliedrele lor duale sunt bitrunchiurile.

Pentru bipiramidele alungite se calculează separat aria laterală a unei piramide A_l3 și aria laterală a prismei intermediare A_l4. Aria bipiramidei alungite A va fi

${\displaystyle A=2A_{l3}+A_{l4}\,.}$

Pentru volum, la fel, se calculează separat volumul unei piramide V₃ și volumul prismei intermediare V₄. Volumul bipiramidei alungite V va fi

${\displaystyle V=2V_{3}+V_{4}\,.}$

Nume	Bipiramidă triunghiulară alungită (J14)	Bipiramidă pătrată alungită (J15)	Bipiramidă pentagonală alungită (J16)	Bipiramidă hexagonală alungită
Tip	Echilateral			Neregulat
Imagine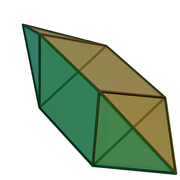
Fețe	6 triunghiuri, 3 pătrate	8 triunghiuri, 4 pătrate	10 triunghiuri, 5 pătrate	12 triunghiuri, 6 pătrate
Dual	Bitrunchi triunghiular	Bitrunchi pătrat	Bitrunchi pentagonal	Bitrunchi hexagonal

• en Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
• en Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN.  The first proof that there are only 92 Johnson solids.

Portal Matematică

• Bipiramidă giroalungită
• Piramidă giroalungită