Poliedru Johnson
(are unghiuri diedre de 180°)
În geometrie, un poliedru Johnson este un poliedru strict convex ale cărui fețe sunt poligoane regulate. Nu există condiția ca toate fețele să fie același poligon sau că aceleași poligoane să se întâlnească în jurul fiecărui vârf. Un exemplu de poliedru Johnson este piramida pătrată echilaterală, J1, care are o față pătrată și 4 fețe triunghiulare. Unii autori cer ca poliedrul să nu fie uniform, adică să nu fie poliedru platonic, poliedru arhimedic, prismă uniformă sau antiprismă uniformă, pe care nu le consideră „poliedre Johnson”.
Ca la orice poliedru strict convex, cel puțin trei fețe se întâlnesc în fiecare vârf, iar suma unghiurilor lor din dreptul unui vârf este mai mică de 360°. Deoarece un poligon regulat are unghiuri de cel puțin 60 de grade, rezultă că cel mult cinci fețe se întâlnesc în orice vârf. Piramida pentagonală (J2) este un exemplu care are un vârf de gradul 5.
Deși nu există nicio restricție evidentă că un anumit poligon regulat nu ar putea fi o față a unui poliedru Johnson, se pare că fețele poliedrelor Johnson care nu sunt uniforme (adică nu sunt un poliedru platonic, arhimedic, prismă sau antiprismă uniforme) au întotdeauna 3, 4, 5, 6, 8 sau 10 laturi.
În 1966, Norman Johnson a publicat o listă care include toate cele 92 de poliedre Johnson (excluzând cele 5 poliedre platonice, cele 13 poliedre arhimedice și infinit de multele prisme și antiprisme uniforme) și le-a dat numele și numerele lor. El nu a demonstrat că există doar 92, dar a conjecturat că nu există altele. În 1967 Victor Zalgaller a demonstrat că lista lui Johnson era completă.[1]
Dintre poliedrele Johnson, girobicupola pătrată alungită (J 37 ), numită și pseudorombicuboctaedru,[2] este unică prin faptul că este uniformă local la nivel de vârf: în fiecare vârf se întâlnesc 4 fețe, iar dispunerea lor este întotdeauna aceeași: 3 pătrate și 1 triunghi. Totuși, ea nu este tranzitivă pe vârfuri, deoarece are izometrie diferită în vârfuri diferite, făcându-l mai degrabă un poliedru Johnson decât un poliedru arhimedic.
Denumiri
[modificare | modificare sursă]Denumirile poliedrelor Johnson se formează pe baza unei formule descriptive flexibile și precise, astfel încât multe poliedre pot fi denumite în moduri diferite fără a compromite acuratețea lor ca descriere. Majoritatea poliedrelor Johnson pot fi construite din primele câteva piramide, cupole și rotonde, împreună cu poliedrele platonice și arhimedice, prisme și antiprisme. În limba română începutul numelui unui anumit poliedru va conține aceste noțiuni. De acolo, o serie de prefixe și sufixe sunt atașate cuvântului pentru a indica adăugiri, rotații și transformări:
- Bi- indică că două copii ale poliedrului respectiv sunt lipite bază la bază. Pentru cupole și rotonde, cele două poliedre pot fi lipite astfel încât fețele lor să corespundă (orto-), sau nu (giro- = rotite). Folosind această nomenclatură, un octaedru poate fi descris ca o bipiramidă pătrată, un cuboctaedru ca o girobicupolă triunghiulară iar un icosidodecaedru ca o girobirotondă pentagonală.
- Alungită indică că o prismă este lipită la baza poliedrului respectiv sau între baze în cazul bi-poliedrelor. Un rombicuboctaedru poate fi astfel descris ca o ortobicupolă pătrată alungită.
- Giroalungită indică că o antiprismă este lipită la baza poliedrului respectiv sau între baze în cazul bi-poliedrelor. Un icosaedru poate fi astfel descris ca o bipiramidă pentagonală giroalungită.
- Augmentată indică că un alt poliedru, și anume o piramidă sau cupolă, este lipită la una sau mai multe fețe ale poliedrului respectiv.
- Diminuată indică eliminarea unei piramide sau cupole de pe una sau mai multe fețe ale poliedrului respectiv.
- Girată indică că o cupolă montată pe sau existentă în poliedrul respectiv este rotită astfel încât diferite margini să se potrivească, ca în diferența dintre orto și girobicupole.
Ultimele trei operații — augmentare, diminuare și girare — pot fi efectuate de mai multe ori la anumite poliedre mari. Bi- și Tri- indică o operație dublă, respectiv triplă. De exemplu, un poliedru bigirat are două cupole rotite, iar un poliedru tridiminuat are trei piramide sau cupole îndepărtate.
La anumite poliedre mari se face distincția între poliedrele la care fețele modificate sunt paralele și poliedrele în care fețele modificate sunt oblice. Para- indică primul caz, că poliedrul respectiv are fețele paralele modificate, iar Meta- indică al doilea caz, că poliedrul respectiv are fețele oblice modificate. De exemplu, un poliedru parabiaugmentat a avut două fețe paralele augmentate, iar un poliedru metabigirat a avut două fețe oblice rotite.
Ultimele câteva poliedre Johnson au nume bazate pe anumite complexe poligonale din care sunt asamblate. Aceste nume sunt definite de Johnson[3] în modul următor:
- O lună este un complex de două triunghiuri atașate la laturile opuse ale unui pătrat.
- Sfeno- indică un complex format din două lune adiacente în lung la nivelul triunghurilor. Bisfeno- indică două astfel de complexe.
- Hebesfeno- indică un complex de trei lune alăturate.
- Coroană este un complex asemănător unei coroane, din opt triunghiuri.
- Megacoroană este un complex mai mare asemănător unei coroane, din 12 triunghiuri.
- Sufixul -cingulum indică o centură de 12 triunghiuri.
Enumerare
[modificare | modificare sursă]Piramide, cupole și rotonde
[modificare | modificare sursă]Primele 6 poliedre Johnson sunt piramide, cupole sau rotonde cu cel mult 5 fețe laterale. Piramidele și cupolele cu 6 sau mai multe fețe laterale sunt coplanare și, prin urmare, nu sunt poliedre Johnson.
Piramide
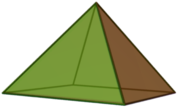
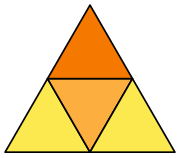
[modificare | modificare sursă]Primele două poliedre Johnson, J1 și J2, sunt piramide. Piramida triunghiulară este tetraedrul regulat, deci nu este un poliedru Johnson. J1 și J2 reprezintă părți ale poliedrelor regulate.
| Regulat | J1 | J2 |
|---|---|---|
| Piramidă triunghiulară (Tetraedru) |
Piramidă pătrată | Piramidă pentagonală |

|
|

|
|

|

|
| Poliedre regulate conexe | ||
| Tetraedru | Octaedru | Icosaedru |

|

|

|
Cupole și rotonde
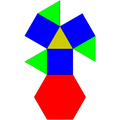
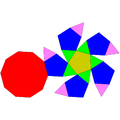
[modificare | modificare sursă]Următoarele patru poliedre Johnson sunt trei cupole și o rotondă. Ele sunt părți ale poliedrelor uniforme.
| Cupolă | Rotondă | |||
|---|---|---|---|---|
| Uniforme | J3 | J4 | J5 | J6 |
| Fastigium (Cupolă digonală) (Prismă triunghiulară) |
Cupolă triunghiulară | Cupolă pătrată | Cupolă pentagonală | Rotondă pentagonală |

|

|

|

|

|
|

|

|
| |
| Poliedre uniforme conexe | ||||
| Cuboctaedru | Rombicuboctaedru | Rombicosidodecaedru | Icosidodecaedru | |

|

|

|

| |
Piramide modificate
[modificare | modificare sursă]Poliedrele Johnson 7–17 sunt derivate din piramide.
Piramide alungite și giroalungite
[modificare | modificare sursă]În piramida triunghiulară giroalungită, trei perechi de triunghiuri adiacente sunt coplanare și formează câte un romb nepătrat, deci nu este un poliedru Johnson.
| Piramide alungite | Piramide giroalungite | ||||
|---|---|---|---|---|---|
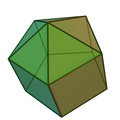
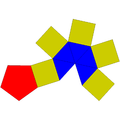
| J7 | J8 | J9 | Coplanar | J10 | J11 |
| Piramidă triunghiulară alungită | Piramidă pătrată alungită | Piramidă pentagonală alungită | Piramidă triunghiulară giroalungită (trapezoedru trigonal diminuat) |
Piramidă pătrată giroalungită | Piramidă pentagonală giroalungită |

|

|
|

|

|

|

|

|
|

|

| |
| Augmentate de la poliedrele | |||||
| tetraedru prismă triunghiulară |
piramidă pătrată cub |
piramidă pentagonală prismă pentagonală |
tetraedru octaedru |
piramidă pătrată antiprismă pătrată |
piramidă pentagonală antiprismă pentagonală |
Bipiramide
[modificare | modificare sursă]Bipiramida pătrată este octaedrul regulat, în timp ce bipiramida pentagonală giroalungită este icosaedrul regulat, deci nu sunt solide Johnson. În bipiramida triunghiulară giroalungită șase perechi de triunghiuri adiacente sunt coplanare și formează romburi nepătrate, deci, de asemenea, nu este un solid Johnson.
| Bipiramide | Bipiramide alungite | Bipiramide giroalungite | ||||||
|---|---|---|---|---|---|---|---|---|
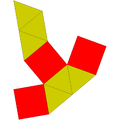
| J12 | Regulat | J13 | J14 | J15 | J16 | Coplanar | J17 | Regulat |
| Bipiramidă triunghiulară | Bipiramidă pătrată (octaedru) |
Bipiramidă pentagonală | Bipiramidă triunghiulară alungită | Bipiramidă pătrată alungită | Bipiramidă pentagonală alungită | Bipiramidă triunghiulară giroalungită (trapezoedru trigonal) |
Bipiramidă pătrată giroalungită | Bipiramidă pentagonală giroalungită (icosaedru) |

|

|

|

|

|

|

|

|

|

|

|

|
|

|

|

|
||
| Augmentate de la poliedrele | ||||||||
| tetraedru | piramidă pătrată | piramidă pentagonală | tetraedru prismă triunghiulară |
piramidă pătrată cub |
piramidă pentagonală prismă pentagonală |
tetraedru octaedru |
piramidă pătrată antiprismă pătrată |
piramidă pentagonală antiprismă pentagonală |
Cupole și rotonde modificate
[modificare | modificare sursă]Poliedrele Johnson 18–48 derivă din cupole și rotonde.
Cupole și rotonde alungite și giroalungite
[modificare | modificare sursă]| Cupole alungite | Rotondă alungită | Cupole giroalungite | Rotondă giroalungită | ||||||
|---|---|---|---|---|---|---|---|---|---|
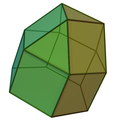
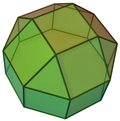
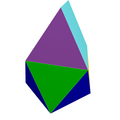
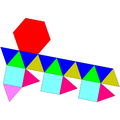
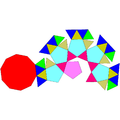
| Coplanar | J18 | J19 | J20 | J21 | Concav | J22 | J23 | J24 | J25 |
| Fastigium alungit | Cupolă triunghiulară alungită | Cupolă pătrată alungită | Cupolă pentagonală alungită | Rotondă pentagonală alungită | Fastigium giroalungit | Cupolă triunghiulară giroalungită | Cupolă pătrată giroalungită | Cupolă pentagonală giroalungită | Rotondă pentagonală giroalungită |

|
|
|

|

|
|

|

|

|

|

|

|

|

|
|

|

|
| ||
| Augmentate de la poliedrele | |||||||||
| Prismă pătrată Prismă triunghiulară |
Prismă hexagonală Cupolă triunghiulară |
Prismă octogonală Cupolă pătrată |
Prismă decagonală Cupolă pentagonală |
Prismă decagonală Rotondă pentagonală |
Antiprismă pătrată Prismă triunghiulară |
Antiprismă hexagonală Cupolă triunghiulară |
Antiprismă octogonală Cupolă pătrată |
Antiprismă decagonală Cupolă pentagonală |
Antiprismă decagonală Rotondă pentagonală |
Bicupole
[modificare | modificare sursă]Girobicupola triunghiulară este un poliedru arhimedic (în acest caz cuboctaedrul), deci nu este un poliedru Johnson.
| Ortobicupole | Girobicupole | ||||||
|---|---|---|---|---|---|---|---|
| Coplanar | J27 | J28 | J30 | J26 | Semiregulat | J29 | J31 |
| Ortobifastigium | Ortobicupolă triunghiulară | Ortobicupolă pătrată | Ortobicupolă pentagonală | Girobifastigium | Girobicupolă triunghiulară (cuboctaedru) |
Girobicupolă pătrată | Girobicupolă pentagonală |

|

|

|

|

|

|
||

|

|

|

|

|

|

| |
| Augmentate de la poliedrele | |||||||
| Prismă triunghiulară | Cupolă triunghiulară | Cupolă pătrată | Cupolă pentagonală | Prismă triunghiulară | Cupolă triunghiulară | Cupolă pătrată | Cupolă pentagonală |
Cupole-rotonde și birotonde
[modificare | modificare sursă]Girobirotonda pentagonală este un poliedru arhimedic (în acest caz icosidodecaedrul), deci nu este un poliedru Johnson.
| Cupole-rotonde | Birotonde | ||
|---|---|---|---|
| J32 | J33 | J34 | Semiregulat |
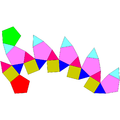
| Ortocupolărotondă pentagonală | Girocupolărotondă pentagonală | Ortobirotondă pentagonală | Girobirotondă pentagonală (icosidodecaedru) |

|

|

|

|
|

|

|

|
| Augmentate de la poliedrele | |||
| Cupolă pentagonală Rotondă pentagonală |
Rotondă pentagonală | ||
Bicupole alungite
[modificare | modificare sursă]Ortobicupola pătrată alungită este un poliedru arhimedic (în acest caz rombicuboctaedrul), deci nu este un poliedru Johnson.
| Ortobicupole alungite | Girobicupole alungite | ||||||
|---|---|---|---|---|---|---|---|
| Coplanar | J35 | Semiregulat | J38 | Coplanar | J36 | J37 | J39 |
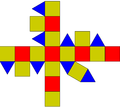
| Ortobifastigium | Ortobicupolă triunghiulară alungită | Ortobicupola pătrată alungită (rombicuboctaedru) |
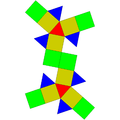
Ortobicupolă pentagonală alungită | Girobifastigium alungit | Girobicupolă triunghiulară alungită | Girobicupolă pătrată alungită | Girobicupolă pentagonală alungită |

|

|

|

|

|

|

|

|

|
|

|
|

|

| ||
| Augmentate de la poliedrele | |||||||
| Prismă pătrată Prismă triunghiulară |
Prismă hexagonală Cupolă triunghiulară |
Prismă octogonală Cupolă pătrată |
Prismă decagonală Cupolă pentagonală |
Prismă pătrată Prismă triunghiulară |
Prismă hexagonală Cupolă triunghiulară |
Prismă octogonală Cupolă pătrată |
Prismă decagonală Cupolă pentagonală |
Cupole-rotonde și birotonde alungite
[modificare | modificare sursă]| Cupole-rotonde alungite | Birotonde alungite | ||
|---|---|---|---|
| J40 | J41 | J42 | J43 |
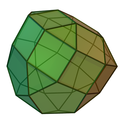
| Ortocupolărotondă pentagonală alungită | Girocupolărotondă pentagonală alungită | Ortobirotondă pentagonală alungită | Girobirotondă pentagonală alungită |

|
|

|

|

|

|

|

|
| Augmentate de la poliedrele | |||
| Prismă decagonală Cupolă pentagonală Rotondă pentagonală |
Prismă decagonală Rotondă pentagonală | ||
Bicupole giroalungite, cupole-rotonde și birotonde
[modificare | modificare sursă]Aceste poliedre Johnson au două forme chirale.
| Bicupole giroalungite | Cupolă-rotondă giroalungită | Birotondă giroalungită | |||
|---|---|---|---|---|---|
| Concav | J44 | J45 | J46 | J47 | J48 |
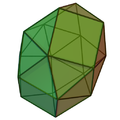
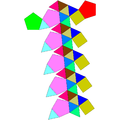
| Bifastigium giroalungit | Bicupolă triunghiulară giroalungită | Bicupolă pătrată giroalungită | Bicupolă pentagonală giroalungită | Cupolărotondă pentagonală giroalungită | Birotondă pentagonală giroalungită |

|
|

|

|

|

|

|

|

|
|

| |
| Augmentate de la poliedrele | |||||
| Prismă triunghiulară Antiprismă pătrată |
Cupolă triunghiulară Antiprismă hexagonală |
Cupolă pătrată Antiprismă octogonală |
Cupolă pentagonală Antiprismă decagonală |
Cupolă pentagonală Rotondă pentagonală Antiprismă decagonală |
Rotondă pentagonală Antiprismă decagonală |
Prisme augmentate
[modificare | modificare sursă]Poliedrele Johnson 49–57 sunt construite prin augmentarea fețelor laterale ale prismelor cu piramide pătrate.
| Prisme triunghiulare augmentate | Prisme pentagonale augmentate | Prisme hexagonale augmentate | ||||||
|---|---|---|---|---|---|---|---|---|
| J49 | J50 | J51 | J52 | J53 | J54 | J55 | J56 | J57 |
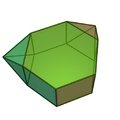
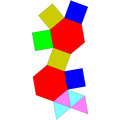
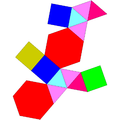
| Prismă triunghiulară augmentată | Prismă triunghiulară biaugmentată | Prismă triunghiulară triaugmentată | Prismă pentagonală augmentată | Prismă pentagonală biaugmentată | Prismă hexagonală augmentată | Prismă hexagonală parabiaugmentată | Prismă hexagonală metabiaugmentată | Prismă hexagonală triaugmentată |

|

|

|

|

|

|

|
|

|

|

|

|

|

|
|

|
|

|
| Augmentate de la poliedrele | ||||||||
| Prismă triunghiulară Piramidă pătrată |
Prismă pentagonală Piramidă pătrată |
Prismă hexagonală Piramidă pătrată | ||||||
Poliedre platonice modificate
[modificare | modificare sursă]Poliedrele Johnson 58–64 sunt construite prin augmentarea sau diminuarea poliedrelor platonice.
Dodecaedre augmentate
[modificare | modificare sursă]| J58 | J59 | J60 | J61 |
|---|---|---|---|
| Dodecaedru augmentat | Dodecaedru parabiaugmentat | Dodecaedru metabiaugmentat | Dodecaedru triaugmentat |

|

|

|

|

|

|

|

|
| Augmentate de la poliedrele | |||
| Dodecaedru și piramidă pentagonală | |||
Icosaedre diminuate și diminuate–augmentate
[modificare | modificare sursă]| Icosaedre diminuate | Icosaedru tridiminuat augmentat | |||
|---|---|---|---|---|
| J11 (Repetat) |
Uniform | J62 | J63 | J64 |
| Icosaedru diminuat (Piramidă pentagonală giroalungită) |
Icosaedru parabidiminuat (Antiprismă pentagonală) |
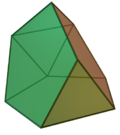
Icosaedru metabidiminuat | Icosaedru tridiminuat | Icosaedru tridiminuat augmentat |

|

|

|
|

|

|

|

|

| |
Poliedre arhimedice modificate
[modificare | modificare sursă]Poliedrele Johnson 65–83 sunt construite prin augmentarea, diminuarea sau girarea poliedrelor arhimedice.
Poliedre arhimedice augmentate
[modificare | modificare sursă]| Tetraedru trunchiat augmentat | Cuburi trunchiate augmentate | Dodecaedre trunchiate augmentate | ||||
|---|---|---|---|---|---|---|
| J65 | J66 | J67 | J68 | J69 | J70 | J71 |
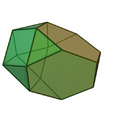
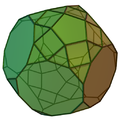
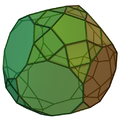
| Tetraedru trunchiat augmentat | Cub trunchiat augmentat | Cub trunchiat biaugmentat | Dodecaedru trunchiat augmentat | Dodecaedru trunchiat parabiaugmentat | Dodecaedru trunchiat metabiaugmentat | Dodecaedru trunchiat triaugmentat |
|

|

|

|
|

|
|

|
|

|

|

|

|

|
| Augmentate de la poliedrele | ||||||
| tetraedru trunchiat cupolă triunghiulară |
cub trunchiat cupolă pătrată |
dodecaedru trunchiat cupolă pentagonală | ||||
Rombicosidodecaedre diminuate girate
[modificare | modificare sursă]| Rombicosidodecaedre girate | |||
|---|---|---|---|
| J72 | J73 | J74 | J75 |
| Rombicosidodecaedru girat | Rombicosidodecaedru parabigirat | Rombicosidodecaedru metabigirat | Rombicosidodecaedru trigirat |

|

|

|

|
|

|

|

|
| Rombicosidodecaedre diminuate | |||
| J76 | J80 | J81 | J83 |
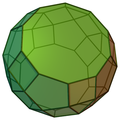
| Rombicosidodecaedru diminuat | Rombicosidodecaedru parabidiminuat | Rombicosidodecaedru metabidiminuat | Rombicosidodecaedru tridiminuat |

|
|

|

|

|

|

|

|
| Rombicosidodecaedre diminuate girate | |||
| J77 | J78 | J79 | J82 |
| Rombicosidodecaedru diminuat paragirat | Rombicosidodecaedru diminuat metagirat | Rombicosidodecaedru diminuat bigirat | Rombicosidodecaedru bidiminuat girat |

|

|

|

|

|

|

|

|
J37 ar apărea și aici ca duplicat (este un rombicuboctaedru girat).
Alte poliedre arhimedice diminuate și girate
[modificare | modificare sursă]Alte poliedre arhimedice pot fi girate și diminuate, dar toate au ca rezultat poliedrele enumerate anterior.
| J27 | J3 | J34 | J6 | J37 | J19 | Uniform |
|---|---|---|---|---|---|---|
| Cuboctaedru girat (ortobicupolă triunghiulară) |
Cuboctaedru diminuat (cupolă triunghiulară) |
Icosidodecaedru girat (ortobirotondă pentagonală) |
Icosidodecaedru diminuat (rotondă pentagonală) |
Rombicuboctaedru girat (girobicupolă pătrată alungită) |
Rombicuboctaedru diminuat (cupolă pătrată alungită) |
Rombicuboctaedru bidiminuat (prismă octogonală) |

|

|

|

|

|

|

|

|

|

|

|

|

|
|
| Girate sau diminuate de la poliedrele | ||||||
| Cuboctaedru | Icosidodecaedru | Rombicuboctaedru | ||||

|

|

| ||||
Poliedre elementare
[modificare | modificare sursă]Poliedrele Johnson 84–92 nu sunt derivate din manipulările „tăiat și lipit” ale poliedrelor uniforme.
Antiprisme snub
[modificare | modificare sursă]Antiprismele snub pot fi construite prin alternarea antiprismelor trunchiate. Girobianticupolele sunt o altă construcție pentru antiprismele snub. Doar antiprismele snub cu cel mult 4 fețe pot fi construite din poligoane regulate. Antiprisma triunghiulară snub este icosaedrul regulat, deci nu este un poliedru Johnson.
| J84 | Regulat | J85 |
|---|---|---|
| Bisfenoid snub ss{2,4} |
Icosaedru ss{2,6} |
Antiprismă pătrată snub ss{2,8} |
| Girobianticupolă digonală | Girobianticupolă triunghiulară | Girobianticupolă pătrată |

|

|

|

|

|

|
Altele
[modificare | modificare sursă]| J86 | J87 | J88 | |
|---|---|---|---|
| Sfenocoroană | Sfenocoroană augmentată | Sfenomegacoroană | |

|

|
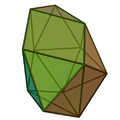
| |

|

|
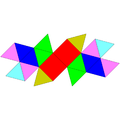
| |
| J89 | J90 | J91 | J92 |
| Hebesfenomegacoroană | Bisfenocingulum | Bilunulăbirotondă | Hebesfenorotondă triunghiulară |

|

|

|

|

|

|

|
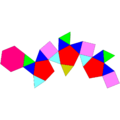
|
Clasificarea după tipul fețelor
[modificare | modificare sursă]Poliedre Johnson cu fețe triunghiulare
[modificare | modificare sursă]Cinci poliedre Johnson sunt deltaedre, având toate fețele triunghiuri echilaterale:
Poliedre Johnson cu fețe triunghiulare și pătrate
[modificare | modificare sursă]Douăzeci și patru de poliedre Johnson au doar fețe triunghiulare și pătrate:
Poliedre Johnson cu fețe triunghiulare și pentagonale
[modificare | modificare sursă]Unsprezece poliedre Johnson au doar fețe triunghiulare și pentagonale:
Poliedre Johnson cu fețe triunghiulare, pătrate și pentagonale
[modificare | modificare sursă]Douăzeci de poliedre Johnson au doar fețe triunghiulare, pătrate și pentagonale:
Poliedre Johnson cu fețe triunghiulare, pătrate și hexagonale
[modificare | modificare sursă]Opt poliedre Johnson au doar fețe triunghiulare, pătrate și hexagonale:
Poliedre Johnson cu fețe triunghiulare, pătrate și octogonale
[modificare | modificare sursă]Cinci poliedre Johnson au doar fețe triunghiulare, pătrate și octogonale:
Poliedre Johnson cu fețe triunghiulare, pentagonale și decagonale
[modificare | modificare sursă]Două poliedre Johnson au doar fețe triunghiulare, pătrate și decagonale:
Poliedre Johnson cu fețe triunghiulare, pătrate, pentagonale și hexagonale
[modificare | modificare sursă]Un singur poliedru Johnson are fețe triunghiulare, pătrate pentagonale și hexagonale:
Poliedre Johnson cu fețe triunghiulare, pătrate, pentagonale și decagonale
[modificare | modificare sursă]Șaisprezece poliedre Johnson au doar fețe triunghiulare, pătrate pentagonale și decagonale:
Poliedre Johnson inscriptibile
[modificare | modificare sursă]25 de poliedre Johnson au vârfurile pe suprafața unei sfere: 1–6,11,19,27,34,37,62,63,72–83. Toate acestea provin din câte un poliedru regulat sau uniform prin girare, diminuare sau disecție.[4]
| Octaedru | Cuboctaedre | Rombicuboctaedre | |||
|---|---|---|---|---|---|
| J1 |
J3
|
J27
|
J4
|
J19
|
J37
|
| Icosaedre | Icosidodecaedre | ||||
|---|---|---|---|---|---|
| J2 |
J11
|
J62
|
J63
|
J6
|
J34
|
| Rombicosidodecaedre | ||||||
|---|---|---|---|---|---|---|
J5
|
J72
|
J73
|
J74
|
J75
|
J76
|
J77
|
J78
|
J79
|
J80
|
J81
|
J82
|
J83
| |
Note
[modificare | modificare sursă]- ^ ru Zalgaller, Victor A. (). „Выпуклые многогранники с правильными гранями”. Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova. 2: 1–221. ISSN 0373-2703. Zbl 0165.56302. Prima demonstrație că există doar 92 de poliedre Johnson. Traduce în engleză: en Zalgaller, Victor A. (). „Convex Polyhedra with Regular Faces”. Seminars in Mathematics, V. A. Steklov Math. Inst., Leningrad. Consultants Bureau. 2. ISSN 0080-8873. Zbl 0177.24802.
- ^ en GWH. „Pseudo Rhombicuboctahedra”. www.georgehart.com. Accesat în .
- ^ en George Hart (quoting Johnson) (). „Johnson Solids”. Virtual Polyhedra. Accesat în .
- ^ en Klitzing, Dr. Richard. „Johnson solids et al”. bendwavy.org. Accesat în .
Bibliografie
[modificare | modificare sursă]- en Johnson, Norman W. (). „Convex Solids with Regular Faces”. Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. ISSN 0008-414X. Zbl 0132.14603. Conține enumerarea celor 92 de poliedre și conjectura că nu există altele.
- en Anthony Pugh (). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 3 Further Convex polyhedra
Vezi și
[modificare | modificare sursă]Legături externe
[modificare | modificare sursă]Materiale media legate de poliedru Johnson la Wikimedia Commons
- fr Gagnon, Sylvain (). „Les polyèdres convexes aux faces régulières” [Convex polyhedra with regular faces] (PDF). Structural Topology (6): 83–95.
- en Paper Models of Polyhedra
- en Johnson Solids de George W. Hart.
- en Images of all 92 solids, categorized, on one page
- en Eric W. Weisstein, Johnson Solid la MathWorld.
- en VRML models of Johnson Solids de Jim McNeill
- en VRML models of Johnson Solids de Vladimir Bulatov
- en CRF polychora discovery project attempts to discover CRF polychora Arhivat în , la Wayback Machine., o generalizare a poliedrelor Johnson în spațiul 4-dimensional
- en https://levskaya.github.io/polyhedronisme/ a generator of polyhedrons and Conway operations applied to them, including Johnson solids.


