Poliedru toroidal

În geometrie un poliedru toroidal este un poliedru care are o topologie la fel cu un toroid (un tor cu o g-gaură), unde g este genul topologic, 1 sau mai mare. Exemple notabile sunt poliedrele Császár și Szilassi.
Variații în definiție
[modificare | modificare sursă]Poliedre toroidale sunt definite prin seturi de poligoane care se întâlnesc pe laturile și vârfurile lor, formând o varietate așa cum o fac. Adică, fiecare latură ar trebui să fie în comun la exact două poligoane, iar în fiecare vârf laturile și fețele care se întâlnesc acolo ar trebui să fie legate între ele într-un singur mod de laturi și fețe alternante. Pentru poliedre toroidale, această varietate este o suprafață orientabilă(d).[1] Unii autori limitează expresia „poliedre toroidale” la poliedre echivalente topologic cu un tor (genul 1).[2]
În acest domeniu este important să se facă distincție între poliedrele toroidale încorporate, ale căror fețe sunt poligoane plate în spațiul euclidian tridimensional, care nu se intersectează între ele și nici nu se autointersectează, de poliedrele abstracte(d), suprafețe topologice fără vreo realizare geometrică.[3] Intermediare între aceste două extreme sunt poliedre formate din poligoane geometrice sau poligoane stelate în spațiul euclidian care au voie să se intersecteze reciproc.
În toate aceste cazuri natura toroidală a unui poliedru poate fi verificată prin orientabilitatea sa și prin faptul că caracteristica Euler nu este pozitivă. Caracteristica Euler se generalizează la , unde N este numărul de găuri.
Poliedrele Császár și Szilassi
[modificare | modificare sursă]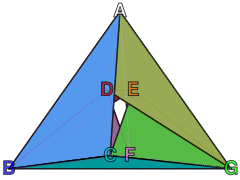 (deschideți și apoi mișcați mausul pentru imaginea interactivă) |
 (deschideți și apoi mișcați mausul pentru imaginea interactivă) |
Două dintre cele mai simple posibile poliedre toroidale încorporate sunt poliedrele Császár și Szilassi.
Poliedrul Császár este un poliedru toroidal cu șapte vârfuri, cu 21 de muchii și 14 fețe triunghiulare.[4] Acesta și tetraedrul sunt singurele poliedre cunoscute în care fiecare segment care leagă două vârfuri formează o latură a poliedrului.[5] Dualul său, poliedrul Szilassi, are șapte fețe hexagonale care sunt fiecare adiacente cu fiecare,[6][7] fapt care oferă jumătate din generalizarea la toruri a teoremei celor patru culori că numărul maxim de culori necesar pentru o hartă pe un tor (care are genul 1) este șapte.[8]
Poliedrul Császár are cele mai puține vârfuri posibile dintre toate poliedrele toroidale încorporate, iar poliedrul Szilassi are cele mai puține fețe posibile dintre toate poliedrele toroidale încorporate.
Toroizii Stewart
[modificare | modificare sursă]O categorie specială de poliedre toroidale sunt construite exclusiv de fețe poligonale regulate, fără intersectări și cu restricția suplimentară că fețele adiacente să nu se afle în același plan una cu cealaltă. Aceștia se numesc Toroizi Stewart,[9] numiți astfel după Bonnie Stewart, care i-a studiat intensiv.[10] Ei sunt anaogii poliedrelor Johnson în cazul poliedrelor convexe; totuși, spre deosebire de poliedrele Johnson, există o infinitate de toroizi Stewart.[11] Acestea cuprind și deltaedrele toroidale, poliedre ale căror fețe sunt toate triunghiuri echilaterale.
O clasă restrânsă de toroizi Stewart, definită tot de Stewart, sunt poliedrele toroidale cvasiconvexe. Acestea sunt toroizii Stewart care cuprind toate laturile anvelopelor lor convexe. La un astfel de poliedru fiecare față a anvelopei convexe fie se află pe suprafața toroidului, fie este un poligon ale cărui laturi se află pe suprafața toroidului.[12]
| Gen | 1 | 1 |
|---|---|---|
| Imagine | 
|

|
| Poliedre | 6 prisme hexagonale | 8 octaedre |
| Vârfuri | 48 | 24 |
| Laturi | 84 | 72 |
| Fețe | 36 | 48 |
| Gen | 1 | 3 | 11 | 3 | 5 | 7 | 11 | |
|---|---|---|---|---|---|---|---|---|
| Imagine | 
|

|

|

|

|

|

|

|
| Poliedre | 4 cupole patrulatere 8 tetraedre |
6 cupole triunghiulare 6 piramide patrulatere |
4 cupole triunghiulare 6 piramide patrulatere |
24 prisme triunghiulare 6 piramide patrulatere 8 tetraedre |
6 cupole patrulatere 4 cupole triunghiulare 12 cuburi |
8 cupole triunghiulare 12 cuburi |
6 cupole patrulatere 12 cuburi |
6 cupole patrulatere 8 cupole triunghiulare |
| Anvelopă convexă | cub trunchiat |
octaedru trunchiat | octaedru trunchiat | cuboctaedru expandat | cuboctaedru trunchiat | cuboctaedru trunchiat | cuboctaedru trunchiat | cuboctaedru trunchiat |
| Vârfuri | 32 | 30 | 30 | 62 | 72 | 72 | 72 | 72 |
| Laturi | 64 | 60 | 72 | 168 | 144 | 168 | 168 | 168 |
| Fețe | 32 | 30 | 38 | 86 | 68 | 88 | 84 | 76 |
Poliedre care se autointersectează
[modificare | modificare sursă] Octahemioctaedru |
 Micul cubicuboctaedru |
 Marele dodecaedru |
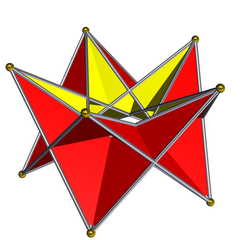
Un poliedru care este format dintr-un sistem de poligoane care se intersectează corespunde unei varietăți topologice abstracte formate din poligoane și sistemul lor de laturi și vârfuri comune, iar genul poliedrului poate fi determinat din această varietate abstractă. Exemplele de poliedre de genul 1 sunt: octahemioctaedrul, de genul 3: micul cubicuboctaedru și de genul 4: marele dodecaedru.
Poliedre coroană
[modificare | modificare sursă]Un poliedru coroană sau stephanoid este un poliedru toroidal, nobil, fiind atât izogonal cât și izoedric. Poliedrele coroană sunt autointersectante, iar din punct de vedere topologic autoduale.[13]
Note
[modificare | modificare sursă]- ^ en Whiteley (1979); Stewart (1980), p. 15.
- ^ en Webber, William T. (), „Monohedral idemvalent polyhedra that are toroids”, Geometriae Dedicata, 67 (1): 31–44, doi:10.1023/A:1004997029852, MR 1468859.
- ^ en Whiteley, Walter (), „Realizability of polyhedra” (PDF), Structural Topology (1): 46–58, 73, MR 0621628
- ^ en Császár, Ákos (), „A polyhedron without diagonals” (PDF), Acta Sci. Math. Szeged, 13: 140–142, Arhivat din original în , accesat în
- ^ en Ziegler, Günter M. (), „Polyhedral Surfaces of High Genus”, În Bobenko, A. I.; Schröder, P.; Sullivan, J. M.; Ziegler, G. M., Discrete Differential Geometry, Oberwolfach Seminars, 38, Springer-Verlag, pp. 191–213, arXiv:math.MG/0412093
, doi:10.1007/978-3-7643-8621-4_10, ISBN 978-3-7643-8620-7.
- ^ en Grünbaum, Branko; Szilassi, Lajos (), „Geometric Realizations of Special Toroidal Complexes”, Contributions to Discrete Mathematics, 4 (1): 21–39, doi:10.11575/cdm.v4i1.61986
, ISSN 1715-0868
- ^ en Szilassi, Lajos (), „Regular toroids” (PDF), Structural Topology, 13: 69–80[nefuncțională]
- ^ en Heawood, Percy John (), „Map colouring theorems”, Quarterly Journal of Mathematics, First Series, 24: 322–339
- ^ en Webb, Robert (), „Stella: polyhedron navigator”, Symmetry: Culture and Science, 11 (1–4): 231–268, MR 2001419.
- ^ en Stewart, B. M. (), Adventures Among the Toroids: A Study of Orientable Polyhedra with Regular Faces (ed. 2nd), B. M. Stewart, ISBN 978-0-686-11936-4.
- ^ en Stewart (1980), p. 15.
- ^ en Stewart (1980), "Quasi-convexity and weak quasi-convexity", pp. 76–79.
- ^ en Grünbaum, Branko (), „Polyhedra with Hollow Faces”, Polytopes: Abstract, Convex and Computational, NATO ASI Series C: Mathematical and Physical Series, 440, Kluwer Academic Publishers, pp. 43–70, doi:10.1007/978-94-011-0924-6_3