CPU design

Denna artikel är tänkt att vara ett försök att förstå och förmedla kunskap om hur en processor eller CPU fungerar och skulle kunna realiseras. Resonemangen bygger på artikeln digitalteknik och den processorarkitektur som där visas längst ner. Processorn är alltså ackumulatorbaserad (AC) vilket är en äldre men väl fungerande arkitektur. I ackumulatorn manipulerar (skiftar mest) och mellanlagrar man data. Hjärnan i processorn är instruktionsregistret (IR). Där realiseras processorns instruktioner i form av små mikroinstruktioner. En svårighet är det som nedan kallats timing. En annan är hur många bitar processorn ska ha. Så länge vi skriver i det kodeffektiva språket assembler så torde 16-bitars adressbuss vara lagom.

CPU'n innehåller varken RAM (annat än som vippor i register) eller ROM (annat än i instruktionsregistret).

Vi säger att det externa programminnet (hårddisk eller PROM) innehåller en instruktion som programräknaren (PC) pekar på. Det kan t.ex vara resetvektorn efter start. Vi antar prilimärt åtta bitar lång data och adressbuss och att POR-kretsen har ställt alla räknare och register. Säg då att PC då står på FFh. Och den fyra bitar långa instruktionsräknaren står på #0000. Den åtta bitar långa OP-koden i instruktionsregistret har också satts av POR-kretsen till säg 00h (som vi låtsas är OP-koden för Reset). Vi antar alltså CISC-arkitektur med upp till 256 OP-koder och maximalt 16 steg att hinna utföra dom.

Eventuellt räcker det med att nyttja halva databussen till OP-koder då vi knappast behöver så många fler än 16 (vilket ger oss tillbaka den galanta RISC-arkiktekturen). Dock bör databussen vara minst åtta bitar om vi ska kunna göra nåt roligt med processorn (även om författaren lyssnat på 5-bitas D/A-omvandlig vilket var gränsen för vad han tyckte lät "bra" på en CTH-laboration i Kommunikationsteori).

Direkt efter spänningspåslag står alltså instruktionsregistret (IR) på OP-koden för Reset (tack vare POR-kretsen). Den lägger då ut en ordledning som möjliggör läsning av innehållet i adress FFh varvid denna adress (resetvektorn) läggs ut på databussen. Dataregistret enablas (EnD_in) samtidigt asynkront mha IR (dock har ingen klockpuls kommit än). När sen E-klockan (som styr allt utom PC) kommer klockas värdet (dvs resetvektorn) in i dataregistret (DR) och är då i praktiken läst. IR står då på adress 001h. Här haltas PC (En_PC=0) och laddning av resetvektorn påbörjas genom att LD_PC samtidigt sätts hög. IR stegar upp till 002h och släpper där haltningen dvs En_PC går hög. När så PC börjar räkna igen pekas adressvektorns data ut i minnet och processen börjar om med att E-klockan laddar DR osv.

Målet är att förstå hur en processor fungerar och hur den skulle kunna realiseras. Pga begränsad överblick har författaren bestämt att vi visar hur en 3-bitars processor skulle kunna realiseras i stället. Vi börjar alltså med att konstatera att både adressbuss och databuss ska vara 3 bitar lång. Vi får då ett adresseringsdjup på 8 vilket innebär max 7 instruktioner förutom Reset. Dataupplösningen blir 8 nivåer.

Följande mnemonics eller OP-koder skall realiseras:

1. 000 RESET
2. 001 LDA ladda A
3. 010 INCA Incrementera A med värdet i B
4. 011 STA lagra A i minnet (RAM)
5. 100 LDB ladda B
6. 101 RORA Rotera höger med 0 in (=/2)
7. 110 ROLB Rotera vänster med 0 in (=*2)
8. 111 JMP Hoppa till valfri början (annars kan det bli problem)

Ett program kan då se ut som följer:

1. $111 RESET(PC=$111, Resetvektor=$000)
2. $000 LDB #001 Sätter värdet för incrementeringen
3. $001 LDA #000
4. $010 STA $000 Sparar i RAM eller LED_A
5. $011 INCA A<-A+B
6. $100 STA $001 LED_B
7. $101 INCA A<-A+B
8. $110 JMP $000

Längre än så kommer vi inte med 3+3 bitar. Tanken med programmet var att en 7-segments LED-display skulle styras med hjälp av CPU'n men vi kommer inte längre än till LED_B innan adresserna tar slut. För varje bits tillägg blir speciellt instruktionsregistret (IR) mer komplext vilket får till följd att man måste programmera ett litet ROM för det. Författaren önskar dock undvika det in i det längsta och avser programmera med hjälp av dioder. Vi skulle också kunna göra så här:

1. $111 RESET(PC=$111, Resetvektor=$000)
2. $000 STA $000 LED_0
3. $001 STA $001 LED_1
4. $010 STA $010 LED_2
5. $011 STA $011 LED_3
6. $100 STA $100 LED_4
7. $101 STA $101 LED_5
8. $110 JMP $000

Detta funkar då vi har tänkt oss LED-signalerna genererade med hjälp av ett permanentminne med dioder. I praktiken borde det vara ett RAM som adresseras och där informationen skrivs men ovanstående är intressant enkelt och fungerar i nuvarande form lika bra om man helt enkelt hänger permanetminnet på adressbussen och låter PC'n gå. Detta eftersom LED-informationen kommer programmeras konsekutivt. Instruktionen STA betyder här alltså att en viss adress sätts upp (som den normalt skriver till). Författaren är osäker på om detta är ett tillräckligt intressant projekt. Det hade varit roligare att skriva till ett faktiskt RAM-minne och göra det på riktigt liksom. På grund av det begränsade adressutrymmet skulle dock bara ett fåtal LED-ar kunna tändas. Detta är för att vi måste ladda ett riktigt värde varje gång och värdet kräver sju bitar då det är sju segment i LED-en. Då har vi plötsligt sju bitars dataupplösning igen och vi närmar oss 8+8 i alla fall.

Efter noggranna övervägningar har vi kommit fram till att verifierandet av vår processorarkitektur skall ske genom att vi använder en fyra bitar lång adressbuss, en tre bitar lång databuss och en två bitar lång IR-buss. Mycket av detta är för att försöka hålla ner komplexiteten (och göra den diskret byggbar). Det har nämligen konstaterats att man inte kan skriva så många instruktioner med hjälp av en tre bitar lång adressbuss. Detta för att instruktionerna i regel innehåller två steg hos PC (instruktion + operand) och därmed adressutrymmet. Att bara tre bitar väljs för databussen har att göra med att det blir lagom stora avkodare då med inte fler än 8 AND-grindar. För en instruktion som JMP skulle dock databussen behöva vara lika lång som adressbussen för den instruktionen lägger ut adressen på databusen men författaren har i stället valt att fylla ut med en instruktion kallad NOP (No OPeration) då den inte innehåller några argument och kan väljas att fylla ut vårt adressutrymme till bristningsgränsen då ju PC bara går runt och initierar en RESET igen. Därför behöver vi ingen JMP-instruktion. Författaren har således valt att realisera tre instruktioner förutom RESET och dessa är LDA, STA och NOP. Märk att vi nu är nere i bara fyra instruktioner. Man kan fråga sig hur man skulle kunna få processorn att utföra nåt vettigt av det men det går faktiskt. Ursprungligen var tanken att vi skulle programmera ett program kallat Pong men författaren insåg rätt snart att tom det enkla programmet kräver lite adresseringsutrymme och har därför valt en annan approach dvs tändning av lysdioder i en punktmatris där lysdioderna kommer att vandra på olika sätt från låg adress till hög adress. På detta sätt kan vi generera sju olika program (det åttonde eller första är ju släckt) genom att främst ändra begynnelsevillkor. Programmet ser ut som följer (där varje rad i programminnet finns med):

1. LDA
2. 7
3. STA
4. 0
5. STA
6. 1
7. STA
8. 2
9. STA
10. 3
11. STA
12. 4
13. STA
14. 5
15. NOP

Kommersiell punktmatris är egentligen ordnad som 5X7 lysdioder men vi använder här bara 3X6. Detta är ett roligt sätt att verifiera vår CPU då vi enkelt kan få punktmatrisen att bete sig annorlunda bara genom att ändra begynnelsevärdet. Om vi till exempel ändrar till 3 (isf 7) kommer bara två kolumner lysa (i takt med vår, i det här testfallet, extremt långsamma klocka, CP).

Genom att skala ner IR-registrets utsignaler till ett minimum så har följande uppsättning konstaterats vara optimal:

u0 Ready
u1 R/W'
u2 LDA
u3 EnA_D
u4 LD_PC
u5 En_PC
u6 En_Im (=PC_out')
u7 EnD_in (=EnD_out')
u8 CS_HD (=CS_RAM')

Allt IR-registret behöver göra för att realisera våra fyra instruktioner är alltså att rycka i dessa tåtar. Författaren har dock fortfarande inte fått riktigt koll på hur och hur timingen blir men experimentbyggen kan få det att klarna. Det verkar emellertid räcka med en enda bit för djupet hos instruktionsrealiseringen. Totalt har vi då tre bitars IRD-information vilket gör den diskreta realiseringen lagom trevligt komplex.

En felaktighet i arkitekturen har påträffats. Detta gäller vår förenkling av att ta bort adressregistret (AR) då programräknaren (PC) lika gärna kan agera register såväl som räknare. Detta är förvisso sant men instruktionen STA implikerar en adress som är skild från PC. I stället för att tillfälligt ställa om PC återinförs AR med three-state buffrar enligt nedan (i listan ovan heter kontrollsignalen En_Im vilket står för Enable Extended vilket är ett processoruttryck för direktadressering).

Våra fyra instruktioner kan realiseras på följande sätt:

OP	IRR	IRC	IRD	DATA
RESET	00	0	1B3h	000 (eller resetvektorn)
LDA	01	0	1A7h	Data
STA	10	0	0C2h	Adress
-	10	1	029h	Data
NOP	11	0	1A3h	-

Detta kommer av att:

u0 1 1 0 1 1
u1 1 1 1 0 1
u2 0 1 0 0 0
u3 0 0 0 1 0
u4 1 0 0 0 0
u5 1 1 0 1 1
u6 0 0 1 0 0
u7 1 1 1 0 1
u8 1 1 0 0 1

där informationen ska läsas från vänster till höger. Längst till vänster står alltså IR-koden för RESET osv.

Efter ytterligare funderingar har vi kommit fram till att vår test-CPU bör byggas med fyra bitar lång adressbuss, fyra bitar lång databuss samt tre bitar lång IR-buss (exklusive den extra biten som IRC står för och som då innebär ett IR-djup på en bit eller två nivåer). Detta för att vi vill att vår CPU skall kunna kallas CPU dvs innehålla en ALU. Vår ALU kommer dock preliminärt bara bestå av en adderare (FA) men detta implicerar en mer komplett arkitektur än ovan. På köpet kommer vi behöva implementera en riktig ackumulator som alltså enligt nedan består av två speciella skiftregister. När vi sedan testar vår CPU kan vi välja att antingen använda ALU'n eller skiftningen (ROR/ROL). Det känns dock tveksamt i nuläget att nåt annat än ALU'n kommer användas då det annars innebär fler u-signaler ut från IR-registret.

Det tråkiga är att nu börjar det redan bli komplext. Dels behöver vi hela 16X4 brytare (där DIP-switchar är att föredra) för att programmera vår CPU. Dels behövs lika många lysdioder för att kunna indikera att processorn fungerar som den ska. Detta hindrar emellertid inte från att vi kan programmera och köra det enkla programmet i kapitel 2 (med det enda tillägget av en bitledning till). Men författaren känner att det roligaste vore om vi kunde verifiera en "riktig" CPU som kan räkna (eller åtminstone addera) i stället för att bara verifiera en sekvensmaskin.

Nu återstår frågan om vi ska implementera ROR/ROL också. Men låt oss ta en titt på vår nya uppsättning nödvändiga instruktioner:

OP-kod IRR
RESET 000
LDA 001
STA 010
NOP 011
INCA 100
DECA 101
LDB 110

I stället för NOP skulle vi kunna implementera JMP vilket vore snyggare men författaren känner fortfarande att NOP räcker för att specificera en instruktion som i princip bara flyttar fram PC så att den går runt och börjar om. Rent arkitektoriskt har detta fusk ingen större betydelse då vi redan har implementerat extended-adressering i form av STA. Programarean är dessutom så liten så att ett par NOP i stället för JMP inte gör någon skillnad. Författaren envisas alltså med detta.

I övrigt tänker vi oss alltså att vi har en LED-matris med 4X16 lysdioder som ska adresseras och tändas enligt vårt testprogram. Först tyckte författaren att det kändes lite meningslöst att bygga en testrigg på detta sätt men hon har kommit på bättre tankar. Ursprungligen var alltså tanken Pong men detta kräver faktiskt en del programmering så nu koncentrerar vi oss på vår LED-matris. Vad kan man då göra med en sådan? Vi har tidigare programmerat för att godtyckligt sätta begynnelsevärdet och få rinnande binärkod. Detta är lite kul för det blir lätt att ändra beteende då bara begynnelsevärdet behöver ändras. Men det blir som sagt ingen riktig verifiering av en riktig CPU. Så nu har tanken blivit att LED-arna kan få rinna från ena hållet till det andra och tillbaks alternativt en gång till när de inte kan rinna mer (8hex). Då har vi två varianter att programmera vilket framför allt innebär involvering av ALU'n. Programmet för växelvist rinnande skulle kunna se ut så här (märk att här hade ROR/ROL passat bra):

1. LDB
2. 0001 (sätter incrementeringsmöjligheten till 1)
   
3. LDA
   
4. 0001 (avser tända lysdiod 1 i första raden/adressen)
   
5. STA
   
6. 0000 (tänder lysdiod 1 i första raden)
   
7. INCA (avser tända lysdiod 2, A<-A+B)
   
8. STA
   
9. 0001 (tänder lysdiod 2 i andra raden)
   
10. INCA
    
11. INCA (avser tända lysdiod 3 med värdet 4)
    
12. STA
    
13. 0002 (tänder lysdiod 3 i tredje raden)
    
14. INCA
    
15. INCA
    
16. INCA
    
17. INCA (avser tända lysdiod 4 i fjärde raden)
    
18. STA
    
19. 0003 (tänder lysdiod 4 i fjärde raden)
    
20. DECA (A<-A-B)
    
21. DECA
    
22. DECA
    
23. DECA
    
24. STA
    
25. 0004 (tänder lysdiod 3 i femte raden)
    

Oj, det gick visst inte så bra då vi bara har 15 adresser förutom RESET att tillgå. Men vi hinner tända lysdiod 3 i tredje raden (av 16). Så här kan vi hålla på. Det bör dock noteras att i stället för att göra upprepade INC/DEC så kan man ladda ett annat värde än ett i B-ackumulatorn men man vinner inte så många adressrader på det ändå. Så hur ska vi summera det här? Ska vi verkligen bygga en fyrabitars processor? Författaren kan inte komma på nåt roligare att demonstrera med än ovanstående men det är ju bara kul för riktiga nördar. Vad finns det annars för roligt man kan göra än en LED-matris? Rinnande ljus är ju heller inte så roligt men där kan åtminstone beteendet relativt enkelt ändras. Här krävs "avancerad" omprogrammering och då bara till en annan typ av rinnande ljus. Känns bara tråkigt och fulltändigt onödigt. Om man inte rent nördmässigt vill verifiera att CPU'n och ALU'n fungerar som dom ska. Måste tänka ut någon annan form av CPU-verifiering. Helst så enkel som möjligt. Alternativt gör vi som i kapitel 2 och leker lite bara. Men det blir ju ingen riktig CPU. Fn också!

Efter lite studier av vad som finns att köpa har vi snopet nog kommit på att SR-vippor inte finns att köpa. Inte i HC-MOS utförande i alla fall. Så vad ska vi nu göra? Ska vi realisera vipporna på grindnivå? Författaren tycker att det vore roligt men har också en känsla för att det blir en väldigt massa virande bara för att realisera en klockad vippa. Det lutar således mer och mer åt CPLD-hållet. För enligt säkra källor kan man välja att antingen bara koda för SR-vippa eller rena grindar. Och projektet sväller nåt extremt om man skulle få för sig att vira grejerna. Författaren är dock väldigt mycket för denna konkreta lösning men bör öppna sig för mer moderna lösningar. Frågan är emellertid om det fortfarande är lönt att realisera en 4-bitars CPU eller om man inte lika gärna kunde satsa på nåt mer användbart dvs 16X8 bitar och alltså konkurrera med en 6809-processor. I det diskreta fallet är det tämligen viktigt att komplexiteten inte sväller men i CPLD-fallet har vi ju kontrollen (och 144 pinnar att tillgå). Där spelar liksom inte antalet bitar så stor roll. Författaren är ambivalent inför dessa möjligheter och tycker att det vore roligast att realisera CPU'n diskret med hjälp av fysiska kretsar men inser samtidigt dom praktiska begränsningarna. Fast författaren vill inte gärna tappa kopplingen med det fysiska då det är alltför lätt att bara skriva kod för vad man vill ha utfört.

Vi säger att vi vill ha två ackumulatorer då det blir mer komplett då. Men vi skippar möjligheten att skifta runt utgående bit (SA) för det är ett sådant extremfall. Vi väljer dessutom att inskift alltid ska vara med 0 dvs vi ska kunna multiplicera med två (ROL) och dividera med två (ROR) och på så sätt kunna manipulera data utan att behöva använda ALU'n. Med tre bitars IRR finns det dock inte utrymme för dessa funktioner varför vi väljer att hoppa över dom. Men detta får till följd att A_in och B_in hårdkodas till noll. Förutom detta implementerar vi både en heladderare (FA) och helsubtraherare (FS) för att kunna implementera funktioner som INCA och DECA. I övrigt är det 4 bitars adressbuss och databuss som gäller med tillägget att IR-bussen bara är tre bitar lång och tillsammans med IRC blir den då också fyra bitar lång. Dvs vi hoppas vi kan realisera alla instruktioner med ett instruktionsdjup på endast en bit (IRC). Hur skulle detta då IR-mässigt se ut? Låt oss se och anta att vi har följande styrsignaler:

u0 Ready
u1 R/W'
u2 LDA
u3 EnA_D
-
u4 EnA_A
u5 LDB
u6 EnB_D
u7 EnB_B
-
u8 En_FA
u9 En_FS
u10 LD_PC
u11 En_PC
-
u12 En_Im (=PC_out')
u13 EnD_in (=EnD_out')
u14 CS_HD (=CS_RAM')

Samt vill realisera följande instruktioner:

1. RESET 6403h
   
2. LDA 6807h
   
3. STA 1009h
   
4. INCA 0103h
   
5. DECA 0223h
   
6. LDB 0023h
   
7. JMP 7003h
   
8. NOP 0001h
   

Vilket ger nåt inte ens författaren riktigt förstår.

Författaren inser att det vore bäst att återgå till den härliga filosofin i kapitel 2. Det enda tråkiga är att vi då bara kan programmera en sekvensmaskin utan beräkningskapacitet. Men projektet blir för stort om vi ska ta med en riktig ALU. En sekvensmaskin är dessutom inte helt fel för det är mycket som måste stämma även där. Med tanke på den kritik författaren fått så kommer det satsas på just det.

Bilden visar en uppgraderad ackumulator. Den här ackumulatorn kan skifta runt utgående bit eller ej (SA_A=Shift Around A). Den kan även sätta ingående bit Ain_A och på så sätt välja om en etta eller nolla ska skiftas in (i detta fall åt höger). Det har även upptäckts att vår CPU behöver tre bussar, D, B och A.

Bilden visar en uppgraderad ackumulator. Skillnaden mellan denna och 2.0 är bara att det är möjligt att ladda ackumulator B direkt från databussen (eller minnet) i stället för att behöva gå via ackumulator A. Ackumulatorerna är således helt fristående med den enda skillnaden att ackumulator A bara kan roteras åt höger (ROR) medan ackumulator B bara kan roteras åt vänster (ROL).

Detta speciella skiftregister är benämnd ackumulator i bilden ovan. Signalerna har ändrat namn men torde vara lätt identifierbara. SR-vippor finns tydligen inte att köpa så vi får antingen bygga dom enligt flanktriggad D-vippa eller använda JK-vippor i stället. Enda skillnaden mellan SR-vippa och JK-vippa är nämligen att tillståndet 11 är tillåtet och innebär togglande av data. Författaren är nog ändå inställd på att bygga dom diskret. En del för att kommersiell JK-vippa triggar på negativ flank av någon anledning (och en inverterare fördröjer signalen). Det går också att bygga en SR-vippa av en D-vippa, som också finns kommersiellt tillgänglig, men den blir något komplex.

Här byter vi alltså ut SR-vipporna mot kommersiellt tillgängliga JK-vippor. Efter lite efterforskningar visar sig detta vara svårare än förväntat. Detta för att JK-vipporna sägs vara av så kallad Master-Slave typ vilket innebär att hela klockpulsen används innan data finns på utgången (och det passar ju inte ihop med vår E-klocka). Det finns dock en kapsel, 74HC109, som är triggad på positiv flank men den har den udda egenheten att ingång K är inverterad (den har dock både asynkron Preset och Clear). Denna skulle man kunna använda. Författaren lutar dock mer och mer åt att realiserad vipporna på grindnivå. Mycket för att det kan vara en fördel om vi skulle få för oss att realisera CPU'n med hjälp av en CPLD.

Här har vi alltså bestämt att vi bara ska ha en en-bits räknare dvs endast en SR-vippa av nåt slag.

Här kan vi använda 74HC74 som är en dubbel D-vippa med asynkron Preset och Clear. Eftersom vi har bestämt att vi ska ha fyra bitars databuss (och adressbuss) så behöver vi två stycken kapslar av denna typ. Vi kan då generera 15 instruktioner exklusive RESET. Vi behöver dock nödvändigtvis inte använda så många bitar som fyra. Vi skulle kunna använda tre och därmed bara dom sju instruktionerna vi beskrivit ovan. Fördelen med tre (+1 för IRC) är att vårt IR-minne bara behöver vara 16 nivåer djupt vilket känns lagom komplext att bygga samtidigt som vi får med lite roliga instruktioner som INCA.

Här bestämmer vi att vi bara ska ha en tre bitar lång IRR. Databussen är fortfarande fyra bitar eller lika lång som adressbussen (för att kunna realisera sådana funktioner som STA). D3 kommer alltså hänga i luften!

Bilden visar vårt andra försök att realisera ett instruktionsregister. Detta är något felritat. IRR och IRC ska nämligen klockas av samma signal dvs kombinationen Ready AND CP, eller egentligen E (se nedan).

Bilden visar ytterligare en uppgradering. Den viktigaste detaljen är att klockpulsen (CP) har bytts ut mot E-klockan. Kodningen har också ändrats något men stämmer ändå inte.

Eftersom vi har att göra med grindfördröjningar så finns inte informationen tillgänglig direkt vid huvudklockans (CP) positiva flank. Man kan alltså inte klocka två enheter efter varandra (på samma buss) samtidigt och förvänta sig att man ska få giltig data. Om vi leker med tanken att det är någon typ av permanentminne (PROM eller HD) som ska läsas så kommer data ut vara "rejält" fördröjd från det att adressen blivit giltig.

Det är käckt att komma på att man kan invertera CP för att få en E-klocka. Denna klocka kan nämligen användas i instruktionsregistret (IR) vilket får till följd att positiv flank hos E-klockan kommer mitt i klockpulsen (CP) dvs vi avsätter praktiskt taget Tcp/2 till fördröjningsproblem.

CP går alltså till programräknaren (PC) där den genererar adresser och E-klockan går till instruktionsregistret (IR) som realiserar OP-koderna genom att rycka i diverse Enable-signaler som till exempel EnD_in.

Nu när vi tänkt till redan från början kan vi bygga en snabb processor...

Här visas lite tydligare vad som normalt händer med adresser och data. Från det att CP gått hög tar det alltså en liten stund innan adressen är giltig (AAV). Därefter tar det ytterligare en något längre stund innan data från minnet är giltig (DAV). Positiv flank hos E-klockan kommer alltså alltid när både adress och data är giltiga. Detta så länge vi inte skruvat upp frekvensen för mycket.

Bilden visar hur CP och E-klockan kan genereras med hjälp av en kristalloscillator och en inverterare. Tack vare denna koppling så kan man utnyttja E-klockan till att utföra saker när data och adresser definitivt hunnit bli giltiga (dvs en halv klockperiod har förflutit innan E-klockans positiva flank kommer i förhållande till CP:s positiva flank).

Bilden visar vår processors uppgraderade blockdiagram. Skillnaden jämfört med 2.0 är att vi måste ha möjlighet att sätta adressen via PROM och databussen när vi skriver till RAM i typiskt en sådan instruktion som STA. Detta kallas för extended-adressering. Alternativet som tidigare skisserats är att vi lagrar informationen där programräknaren (PC) råkar stå. Detta fungerar också men är osmidigt bl.a ur demonstrationssynpunkt. Vi har dessutom ändrat signalerna från X<Y och Y=Y då svaret från dessa jämförelser naturligtvis inte är en buss med signaler utan endast en. Författaren är dock tveksam om de bör användas som datasignal (alltså en del av databussen) eller om nåt speciellt flagg-register (typ CCR) i stället borde användas. STA innebär alltså att först måste instruktionsregistret (IR) ta över adressbussen från programräknaren (och lagra den i adressregistret, AR) sedan lägga ut data och skriva till den, av AR tillfälligt lagrade, adressen. Minnet måste med andra ord först adresseras innan det kan skrivas.

Bilden visar vår processors uppgraderade blockdiagram. CS_RAM och CS_HD är två egentligen onödiga signaler då Chip Select (CS) normalt avkodas utifrån respektive enhets adressarea. Till exempel så kan man avkoda HD att jobba mellan 0000h och 0FFFh och RAM mellan 1000h och FFFFh. Vi har här valt separat Chip Select då det blir smidigare samt utnyttjar adressutrymmet bättre. CS är alltså mer eller mindre samma sak som Output Enable (OE) som förklaras bättre i samband med three-state. Versionen saknar adressregister (AR) då vi kommit på att detta är nödvändigt för extended-adressering (STA). Pre-fetch funktionen kan dock fortfarande vara bra för det gäller som sagt att IR-registret (IRR) alltid initialt måste kunna läsa databussen (utom när den själv styr). CP är dessutom kopplad till ackumulatorn (AC). E-klockan bör nog kopplas dit i stället.

Bilden visar en uppgradering av vårt dataregister. Det har tillkommit en finess som liknar pre-fetch dvs databussen enablas för inkommande data innan den första instruktionen. Data kommer då garanterat ligga inne på databussen och IR kan fungera som det ska.

Bilden visar en uppgradering av vårt dataregister. Vi har här minimerat antalet styrsignaler genom att helt enkelt påstå att om databussen är enablad för ingående data (EnD_in) så är samtidigt databussen disablad för data ut (EnD_out). Och vice versa. Vi har preliminärt kvar finnessen för pre-fetch.

Efter lite funderingar har vi kommit fram till att vi trots allt måste ha ett separat adressregister. Detta för att möjliggöra direkt (eller så kallad extended)-adressering dvs adressbusssen måste tillfälligt kunna tas över av databussen och därmed minnet för att vi ska kunna kontrollera vart i RAM vi lagrar saker och ting. Tidigare version fungerar också men blir beroende av vad PC råkar ha för värde och är ett inte lika smidigt sätt att demonstrera vår CPU:s funktion på. En_Im står för Enable Extended. Det betyder att antingen tar minnet (databussen) över adresseringen eller också gör programräknaren (PC) det.

Efter ett års funderande har författaren kommit fram till att en asymmetrisk 8*16-bitars arkitektur är den mest optimala. Detta för att man dels kan skriva programmen på ett överskådligt sätt (läs två hexadecimala symboler för data och fyra för adress) dels är det enkelt att få tag i periferikretsar såsom EPROM och RAM mm. Det är dessutom inget som hindrar att man utökar till godtycklig asymmetrisk arkitektur modell 16*32. Enda hindret såsom författaren ser det kan vara periferikretsarna. I vilket fall som helst kommer man, ur mer än demosynpunkt, långt med vald arkitektur dvs typiskt 32kB stort program. Enda problemet med asymmetrisk arkitektur är att processorn blir aningen mer komplex än nödvändigt.

Bredvid visas en bild av ett första försök att realisera en CPU. Denna CPU har även ett indexregister (X-Reg) implementerat. Efter noggranna funderingar kan dock inte författaren riktigt komma på den stora vitsen med ett indexregister så det är borttaget i den enklare processorn enligt nedan. Som kuriosa kan nämnas att indexregister inte användes i processorer förrän efter 1949 (allt enligt engelska Wikipedia). Eftersom det då gick att inte använda indexregister och eftersom författaren har en förkärlek för det enkla så har vi tagit bort indexregistret. Ackumulatorn A (ACC_R + ACC_L) har däremot försökts implementeras på ett riktigt sätt. Såvitt författaren kan förstå är en ackumulator en kombination av tre saker dvs parallellt laddningsbart register, upp/ned-räknare och skiftregister. Upp/ned-räknarfunktionen används i samband med incrementeringar (INC) eller decrementeringar (DEC). Skiftregisterfunktionen används i samband med multipliceringar (LSL) eller divideringar (LSR) med multiplar om två. Registerfunktionen (LDA/STA) är dock den vanligaste funktionen.

I den enklare arkitekturen har vi dels tagit bort indexregistret dels tagit bort möjligheten att nollställa carry (C_CL) dels förenklat ackumulatorn (A) till att bara bestå av parallellt laddningsbara skiftregister (SR_R + SR_L) dels tagit bort den extra inverteraren dels förenklat stackpekaregistret (SP) (man skulle också kunna förenkla programräknaren (PC) på liknande sätt som SP men författaren har av rittekniska skäl inte gjort den förenklingen). Finessen med att ta bort C_CL är att två typer av additionsinstruktioner ändå kommer att realiseras (så det finns inget behov av C_CL). Den ena, ADD, adderar två (heltal) utan hänsyn till inkommande carry (som lagras i CCR). Den andra, ADC, adderar två tal med hänsyn tagen till om det genererats carry vid föregående aritmetiska operation. Om man exempelvis adderar PC_LB med ett relativt (två-komplement) branch-hopp såsom BEQ och får carry ut kan man sedan addera 0+C+PC_HB (mha ADD_00+ADC) och få PC_HB ut. Som konsekvens av att vi förenklat ackumulatorn kommer vi att behöva realisera dom mycket enkla instruktionerna INCA respektive DECA mha heladderaren (FA). Detta skulle ungefär kunna gå till på följande sätt (läs på mikroinstruktionsnivå): Först laddas A med värdet (t.ex LDA #$FE), sedan läggs värdet ut på ALU-bussen mha styrsignalen ALU. Sedan sätts styrsignalen ADD_01 hög (och ADC låg) varvid värdet $01 adderas till värdet på ALU-bussen. Vid nästa klockpuls (CP) laddas A med det inrementerade värdet (när LDA går hög). Om vi i stället vill decrementera A så kan vi göra på liknande sätt fast med styrsignalen ADD_FF (=-1) hög. Detta får naturligtvis till följd att processorn blir lite långsammare än optimalt men vi får se om vi kanske kan få ordning på en riktig ackumulator så småningom.

Detta avsnitt avser inte tillfullo förklara valda arkitekturs funktion. Meningen är mest att nämna finesserna och hur tankegången varit kring dom.

När man studerar den enklare arkitekturen så ser man bl.a att E-klockan genereras på ett felaktigt sätt. Den ska bara vara förskjuten så pass mycket att data finns tillgänglig på databussen när minnet har adresserats (kallas accesstid). När man dock tittar på hur pass snabb en HC-MOS 7400 är så räcker det inte med fyra inverterare i rad (typiskt 80ns) för att man ska kunna använda lite äldre minnen (typiskt 150ns EPROM 27C256-15). Här har det antagits att en modern CPLD är av CMOS-typ. Lösningen skulle antingen kunna vara att låta E-klockan vara inversen av CP (varvid 3MHz blir max klockfrekvens med valt minne) eller att man låter E-klockan genereras externt av en riktigt slö krets såsom 4000-serien.

CCR (Condition Code Register) signalerar hur en aritmetisk operation har utfallit. Den indikerar med så kallade flaggor om svaret är noll (Z=1), negativt (N=1), för stort (C=1) eller overflow (V=1) där V-flaggan är den mest skumma då den hanterar specialfallet att operanderna kanske båda är positiva men att svaret ändå blir negativt (ur två-komplementperspektiv). Tänk er till exempel att tallängden är -128 till +127 för en byte. Om då 30 ska adderas till 100 blir det overflow. Författaren hade mycket svårt för tvåkomplement i början men tycker numera att det är enkelt. Instruktionen NEGA inverterar till exempel ett tal i ackumulatorn och adderar ett varvid vi får det negativa talet på tvåkomplentsform. Förutom vid overflow så blir talet rätt både på negativ och positiv form. Talets värde beror helt enkelt bara på hur du ser på det. Addera till exempel 2 (0010) med C (1100) som är -4 eller 12. Svaret blir E som är -2 eller 14.

SP (Stack Pointer register) är en parallellt laddningsbar upp/ner-räknare. Den initieras preliminärt till 00FF vid RESET. Den kommer dock kunna ställas till godtycklig adress med hjälp av instruktionen LDS. Dess användning är nödvändig för att kunna använda sig av subrutiner (JSR). Vad den gör är att den väntar på en så kallad PUSH/PULL-instruktion (speciellt PSH_PC som dock bara används internt) iom JSR varvid återhoppsadressen PC_LB läggs på 00FF och PC_HB på 00FE.

Ackumulatorn (SR_R+SR_L) består av två parelellt laddningsbara skiftregister. Den är uppdelad i två delar för att kunna skifta höger (division med multiplar om 2) respektive vänster (multiplikation med multiplar om 2). En riktig accumulator borde även kunna utföra INC/DEC varvid en upp/ner-räknefunktion bör införas. Det har och kommer skissas på en sådan lösning men preliminärt nöjer vi oss med det enkla och löser INC/DEC mha heladderaren (FA). Eftersom man måste kunna skifta åt båda hållen måste ackumulatorn bestå av två separata enheter. Det har införts en minnesfunktion (L/R'+LD_D) för att komma ihåg vilken enhet som senast användes. Det har även spekulerats i om man kan eller inte kan göra omväxlande skiftningar åt höger och vänster. Författaren tror att fördröjningen i three-state buffern är tillräcklig för att värdena inte ska hinna förändras när de läggs ut på databussen och samtidigt klockas in i den andra enheten. Dock är detta mest spekulationer så det rekommenderas att värdet först mellanlagras i minnet innan man byter skiftriktning. Samtidigt är frågan hur ofta man gör på ovanstående vis.

Mha signalen STA läggs ackumulatorvärdet ut på databussen (D) och mha signalen ALU läggs data ut på ALU-bussen (A). Alla aritmetiska (FA) och logiska (AND, OR, XOR) operationer får då en särskild buss som är styrd av ackumulatorn. Den lågiska operationen INV eller NOT är hårdkodad till att höra ihop med heladderaren (FA).

Programräknaren (PC) består av en parallellt laddningsbar räknare. Den har fått separata laddningsregister för HB respektive LB men detta är inte nödvändigt. Den har också utgångsbuffrar med vilka man kan läsa värdet hos PC för att till exempel göra branch-hopp (typ BEQ). Efter PC kommer adressregistret (AR). Detta är också laddningsbart med LB och HB separat (för vi har ju en asymmetrisk arkitektur). Det finns även en styrsignal som heter EXT med vilken adresseringsmoden EXTENDED menas. Vilket betyder att adressbussen kortvarigt tas över av instruktionen (typ STA $AAFF) för att i det här fallet skriva i minnet varefter kontrollen återlämnas till PC.

Databussen (DB) innehåller inga register. Detta för att författaren fått för sig att det inte behövs och till och med förstör synkronismen då data är tillgänglig först t_acc efter det att minnet adresserats (kallas också DAV eller DAta Valid). Föreställ er nu att minnet adresseras och minnesadressen klockas ut med positiv flank på CP (Clock Pulse). Detta samtidigt som vi har ett instruktionsregister (IR) som jobbar med E-klockan som klocka (vilket ska vara en klocka med positiv flank gott och väl fördröjd med minst t_acc). Vid E-klockan kan vi i lugn och ro läsa relevant data. Skulle vi dock ha ett register emellan så skulle vi behövt klocka det också och det med E-klockan och sen hade vi behövt en tredje typ F-klocka för att klocka instruktionsregistret. Detta samtidigt som vi hade fått en fördröjning på en klockcykel. Som det är nu har vi endast en fördröjning av PC relativt data in/ut. Detta för att först stegas PC, sen stegas AR och pga E-klockan i IR så hinner inte PC stoppas varvid PC står på nästa instruktion när adressen ut från AR är riktig. Nåt sånt tror författaren att det blir.

Instruktionsregistret (IR) består av fyra delar. Två paralellt laddningsbara register (IRR+BR), en räknare (IRC) och ett minne (ROM) där dom valda instruktionerna realiseras i form av mikroinstruktioner. In till IRR (Instruction Register Register) kommer alla instruktioner i form av en OP-kod som den alltid känner igen (man kan undra varför men det hänger helt enkelt på starten av sekvensmaskinen dvs Reset måste lyckas. Förutom att du programmerat rätt med rätt antal operander till op-koden som i vårt fall bara består av 0, 1 eller 2 operander. OP-kod + operand bildar sedan en instruktion). Op-koderna bildar sedan en del av adressen till ROM. I det här fallet hög byte. In till BR (Branch Register) kommer sedan flaggorna N's och Z's värde som bildar input till IR. På sättet vi löst det kommer dessa ingångar bara vara garanterat noll efter reset och sedan anta N's och Z's värde efter första använda Branch-instruktion. Därefter har vi ingen möjlighet att nollställa dom. Om man inte med vilje gör en addition av två positiva tal samt en dummy-branch. Författaren tror inte det fungerar och vill inte krångla till programmeringen så vi får helt enkelt finna oss i att BR inte alltid är noll och programmera våra mikroinstruktioner på fyra olika adresser (dvs alla N's och Z's kombinationer. Varav en eller två är riktiga). IRC (Instruction Register Counter) har 16 steg. Den stegar igenom de sekvensiella mikroinstruktionerna där vi rycker i olika tampar såsom LDA i schemat ovan. Allt detta programmeras sedan i ett EPROM (här kallat ROM). Detta sägs kunna göras i en CPLD vilket vore en fördel för antalet styrsignaler är många och ett lättanvänt typ 32-bitars minne kan vara svårt att få tag i.

Vidstående bild visar vald arkitektur. Ändringarna är dels att hög nibbel i CCR är nollställd, E-klockan är inversen av CP samt en modifiering av instruktionsregistret som gör att man inte kräver att man tar hänsyn till alla fyra kombinationerna av N och Z-flaggorna. Flaggorna nollställs helt enkelt då varje instruktion är klar (Ready) samt laddas då instruktionen kräver det (Branch). Att vi lite okonventionellt har valt att använda inversen av CP som E-klocka har helt enkelt med att göra det som nämns i kommentarerna ovan dvs att moderna kretsar är för snabba för vårt gamla minne. I och med vald typ av E-klocka kan man dock skruva upp frekvensen efter hand och begränsningen är bara att t_acc < T_cp/2. Det har framkommit att instruktionen CMP blir väldigt knölig att realisera med vald arkitektur. Många gånger använder man fördröjningar modell

LDA #$FF
Loop:DECA
CMP #$00
BNE Loop

där Lopp egentligen har värdet -5 (eller FB) eftersom den hoppar över 5 bytes inklusive sig själv.

I ovanstående exempel ser vi att det decrementerade värdet av A måste sparas och får inte skrivas över. Vi kan därför inte återanvända A till att generera A-M som är vad CMP gör (dock utan att lägga tillbaks resultatet i A). Vi måste alltså mellanlagra A medans vi gör NEGA (A<- -A). Enda sättet förutom extra ackumulator eller extra heladderare (eftersom det egentligen är två aritmetiska operationer vi gör när vi subtraherar dvs A+M'+1) är att mellanlagra DECA på stacken. Detta låter sig dock inte så enkelt och snabbt göras men det går och är den enda lösning författaren kan komma på.

Bilden visar timingen hos vår processor. Det som är viktigt att komma ihåg är att E-klockan kommer efter klockpulsen (CP). I vårt fall T_cp/2 efter CP. Detta betyder att den information som finns efter adressering (se DAV eller Data Valid) kommer (eventuellt) att klockas in i instruktionsregistret (IR). Detta vid positiv flank hos E-klockan som normalt sett bara är lite förskjuten i förhållande till CP. I vårt fall kommer alltså positiv flank hos CP först och därefter positiv flank hos E varvid informationen klockas in. Det är viktigt att förstå detta när vi senare programmerar IR. Ett aber med vår arkitektur är att adressregistret (AR) är uppdelat på två register som vardera kan laddas individuellt med var sin byte. Vi hade dock behövt ett till register ty när vi gör en extended-adressering laddas först HB i ena registret varvid en vild adressering under en klockcykel sker eftersom LB inte är laddad än. Efter noggranna funderingar har det dock framkommit att denna vilda adressering inte spelar någon roll. Oavsett om R/W' är hög eller låg. Detta dels för att IR kör sin mikroinstruktion och är inte mottaglig för fler instruktioner. Dels är R/W' normalt hög då vi läser från programminnet (PROM).

Bilden visar ett exempel på minneskonfigurering. Det har inte avsetts att beskriva en hel dator utan fokus ligger på processorn (dock kommer processorn behöva testas på nåt sätt så i slutändan blir det nog att bygga en dator ändå även om det finns andra sätt att verifiera funktionen). Även om man normalt sett inte måste tänka på minneskonfigureringen när man designar en processor så är det en fördel. Vi har t.ex signalen OE som här är genererad internt (som inversen av R/W') i processorn men som emellertid lika gärna kunde ha genererats externt. När det gäller processorn och I/O-enheter är mest valet av interrupt (IRQ) eller inte intressant. Vi har dock valt att inte implementera IRQ. Detta dels för att det komplicerar arkitekturen dels för att polling är en underskattat metod att känna av externa enheter. Stackpekarregistret (SP) är hårdkodat till $00FF (där alltså RAM bör ligga). Detta kan dock ändras mha den egenhändigt påhittade instruktionen LDS.

Bilden visar ett förfinat exempel på minneskonfigurering. Tanken här är att vi bara har två I/O-enheter som hänger på samma adress(area). En keyboard eller någon typ av A/D som levererar ett trivialt digitalt värde när det inte är aktivt, t.ex FF. Om det gör det kan det nämligen pollas för godtyckligt annat värde. Den andra enheten, här kallad monitor, kan också vara ett enkelt sifferdisplay (2X7-segment) med ett register där data klockas in varje gång CS går hög samtidigt som R/W' går låg (vilket är ekvivalent med STA i aktuellt adressområde t.ex $4000). När adressarean är vald styr alltså R/W' (läs LDA/STA) vilken av enheterna som skall beaktas. Adressavkodningen skulle kunnat gjorts effektivare men det blir rittekniskt klumpigt.

Bilden visar valda instruktioner och deras kodning. OP-koderna (Opcode) är f.ö plankade från HCS08. Detta för att slippa designa en egen kompilator och även om man faktiskt kan programmera i ren maskinkod så är minst assembler att föredra. Att försöka programmera i C är dock förmodligen att hoppas på för mycket. Främst för att vi dels valt ett så snävt urval av instruktioner dels för att vi inte har nåt indexregister (X-Reg). Assembler kommer man dock långt med.

Förutom HSC08-instruktioner så har vi hittat på två instruktioner, LDS (Load Stackpointer) och NOTA (Logical NOT). Dom är så finurligt valda att man kan skriva LDHX # respektive RSP i kompilatorn för att generera rätt maskinkod. Vad som kan vara förvirrande är att det i fallet LDS krävs två byte vid immediate-adresseringen (jj kk) medans det i NOTA-fallet inte krävs nån operand alls (då den jobbar på redan befintliga operander nämligen ackumulator A's värde. Denna adresseringsmod kallas också Inherent). Vi gör ett försök att förtydliga detta. Dom adresseringsmoder vi använder i vår CPU är tre. Immediate, Extended och Inherent. Immediate betyder att data kommer direkt från PROM (och är alltså fix och normalt bara en byte. Detta är markerat med "dd" under Operand). Extended betyder att data skrivs eller läses från RAM eller I/O-enheter. Denna typ av data kan man kalla vara variabler. Detta är markerat med "hh ll" för att visa att vi här behöver två byte lång operand (h som i high, l som i low) då vi adresserar minnesarean som använder 16 bitar. Inherent betyder att vi inte behöver några operander då informationen finns latent i processorn (t.ex INCA).

Här har det kämpats och det är förmodligen långt ifrån rätt. Det som slår en när man försöker mikroprogrammera är emellertid att instruktionsdjupet blir rätt stort dvs alla instruktioner kräver bra mycket fler klockcykler än HCS08. Exempelvis kräver EOR $ femton klockcykler medans HCS08 löser det på fyra. NEGA löser vi på 3 medans HCS08 bara behöver 1 osv. Så det blir en långsam processor vi bygger. Men det känns som den ska kunna fungera och uträtta det vi vill. Mest hoppas författaren på att vi kan programmera dessa mikroinstruktioner i CPLD'n så vi slipper nåt externt 41-bitarsminne. Det var hemskt vad komplexiteten rusade iväg när vi väl bestämt oss för att bygga nåt användbart.

Vad som oroar författaren är återigen timingen. Vi har inte tillräcklig koll på vad som händer när fetch-instruktionen kommer. Som det är nu är det tänkt att den alltid avslutande mikroinstruktionen AR, som uppdaterar adressregistret, ska flytta PC till nästa instruktion samtidigt som den enablar för läsning av den instruktionen. Men hur blir det med klockningen egentligen? Om Ready avslutar realiseringen av instruktionen kan den då samtidigt fås att ladda in nästa instruktion (för om vi gör rätt kommer det ALLTID ligga en ny instruktion och vänta när Ready kommer)? Vi har ju synkronismen att E-klockan går hög mitt i CP vilket verkar ge den trevliga funktionen att vi kan göra två saker samtidigt då vi kan OE-enabla och klocka in resultatet samtidigt för OE hinner lägga ut sina signaler innan CP kommer en halv klockcykel senare. Författaren är dock väldigt osäker på detta.

Ett sätt att snabba upp processorn vore att lägga till ett temp-register som bara används internt och som kan lägga ut data både på ALU-bussen och D-bussen. För ett problem är att vi inte kan ändra adressregistret (AR) förrän båda byten är hämtade (i t.ex en ORA $-instruktion). Vi har därför behövt mellanlagra HB i A vilket fått tillföljd att A har måst pushas undan på stacken innan mellanlagringen och sedan pullas tillbaka när vi hämtat värdet och kan utföra operationen. Vi skulle med ett tempregister kunna snabba upp processorn minst 30%. Ett annat sätt att snabba upp den vore att göra det möjligt att nå "ovansidan" av adderaren (FA) med hjälp av införande av ett par three-stateregister. Att hela tiden gå via FA ger oss också den bonusfinessen att alla tal kan CCR-checkas (Z=1 för noll osv).

Brancharna har varit lite speciella att implementera. När någon av de fyra valda branchernas op-kod laddas in i instruktionsregistret (IR) så kommer alltid flaggorna N och Z omedelbart laddas in då Branch går hög. Vi får alltså skenbart fyra olika tillstånd att avkoda. NZ=11 finns dock inte då N jobbar på b7 och Z är NOR på alla bitar så talet kan inte både vara negativt och noll varför NZ=11 utgår. Kvar har vi NZ=00, 01 och 10. NZ=00 innebär att talet inte är negativt och samtidigt inte är noll, alltså >0. NZ=01 innebär att talet är noll och NZ=10 innebär att talet är <0. Som exempel kan nämnas att för BPL så ska vi utföra branchen när NZ är 00 men gå ur och generera Ready för de andra två fallen. När det gäller BNE måste vi dock utföra branchen för två kombinationer (00 och 10) samt gå ur enbart vid 01.

Vi ska här försöka förklara lite av anteckningarna. AR betyder som sagt att adressregistret uppdateras (med LD_AR_HB respektive LD_AR_LB). Detta måste alltid göras då man endera byter från Extended-adressering (EXT) eller stegat PC (EN_PC). Vi har antagit att opkoden laddas in korrekt varvid vi alltid (förutom i Inherent fallet) måste stega fram till första operanden (PC+1, AR). Vi ska här passa på att förtydliga att vår programräknare (PC) alltid stegar en enda byte åt gången och enligt minneskonfigureringen ovan så har vi konventionen att högst adress är nedåt. PC stegar alltså alltid från låg adress och således nedåt i figuren (räknar dock alltid upp). Efter Reset börjar den med första OP-koden varvid den i det extremaste fallet behöver stegas ytterligare två byte för att läsa in alla operanderna. Lagringen i PROM är, i enlighet med PC's stegriktning, OP-kod (1 byte), Operand 1 (1 byte) och Operand 2 (1 byte) där Operand 1 alltid är hög byte (HB) och Operand 2 låg byte (LB). När tilldelning skett utifrån så har det indikerats med en pil åt höger. Intern tilldelning såsom lagring i Ackumulator har alltid indikerats med en pil åt vänster. Allt som eventuellt ligger på databussen har benämnts M (som i Memory).

Bilden visar hur relativa branch-hopp görs. Det har här av enkelhetsskäl antagits att PC bara är en byte stor och att våra hoppmöjligheter således bara är +7/-8 (jämför +127/-128 för en byte). Anledningen till att detta tas upp är att det helt enkelt har smugit in sig ett fel i vår arkitektur. När pc skall stegas negativt (jfr 26+(-8)) blev inte hög byte att "rulla runt" neråt. Detta fungerade bara uppåt (pga carry. Se 2C+5). Vi måste med andra ord hålla reda på om offset är av negativt slag (b7=1) eller av positivt slag. I det positiva fallet adderar vi således PC_HB+ADC+ADD_00 samt i det negativa fallet adderar vi PC_HB+ADC+ADD_FF. Att det blir på detta sätt förklaras i bilden.

CPU_1.2 kommer således hårdkoda detta med hjälp av en ny styrsignal kallad ADD_HB. Denna får dataposition d41 och blir bara att påverka data för brancherna. Att vi behöver använda carryflaggan både uppåt och neråt bevisas av 2C+5 respektive 28+(-8). Det är även intressant att notera V-flaggans aktivering vid 26+3 (vi har ju max 27 eller snarare 7 här). Det här var inte helt lätt att få ordning på. Författaren nödgades ta hjälp av kollega men känner att hon kanske förklarar lite dåligt. Det bör påpekas att vi här använder oss av två-komplement vad beträffar offseten. Ett negativt tal representeras alltså av inversen av talet man vill göra negativt plus ett. På detta sätt får man en cirkulär talrepresentation där till exempel negativa tal har 1 i högsta biten (MSB) och där -1 representeras av idel ettor. I övrigt finns en bra artikel om två-komplement på Wikipedia.

Bilden visar en uppgraderad version av vår CPU. Detta visade sig nödvändigt då processorn ej kunde göra negativa branch-hopp ordentligt. Detta har nu hårdkodats och aktiveras av styrsignalen ADD_HB som enligt ovan får dataposition d41 och bara kommer påverka data för brancherna. Vi kommer inte ändra i mikroinstruktionerna ovan utan nöjer oss med att påpeka att istället för ADD_00 ska ADD_HB användas.

Flaggan har fått det något missvisande namnet H. H står normart sätt för Half Carry vilket inte avses här. Dock är det ett slags half carry om man ser på byte-nivå. Positiv offset, ADD_00 med carry. Negativ offset, ADD_FF med carry.

Bilden visar en testrigg för vår CPU. Ett binärt värde ställs in mha BCD-omkopplarna (MSB uppåt). Medans man gör det registreras värdet av lysdioderna längst till vänster. När man ställt in värdet man vill ha trycker man på den återfjädrande omkopplaren SW1. Värdet klockas då in till lysdiodsarrayen näst längst till vänster. Detta synkroniserar eventuell läsning från CPU'n via andra HC374'n från vänster. Vi kallar denna oktala D-vippa för IC2. Värdet in på IC2 fortplantar sig sedan till databussen när CS är aktiv samtidigt som R/W' är hög. Åt andra hållet skrivs värdet till den nedre HC374'an (IC3) och därmed lysdiodsarrayen när CS är aktiv samtidigt som R/W' är låg. Som vi byggt upp minneskonfigureringen enligt ovan kan vi skriva och läsa till samma I/O-adress (t.ex $4000) varvid vi vid lästillfället får värdet från BCD-omkopplarna och vid skrivtillfället får IC3 att tända sina lysdioder.

Vi har även lagt till LED-indikationer på databuss såväl som adressbuss och dessutom CS och R/W'. Ska man få nån nytta av dessa finesser får man dock vara expert på hexkod (alla LED's kommer grupperas i grupper om fyra för enkelhets skull).

Ett aber med vår testrigg är dom vilda adresseringarna som tidigare nämnts. Dessa sker dock bara under en klockcykel. Detta komer alltså att stabilisera sig för varje tryck på vår manuella klocka (SW2) då IR bara kommer att fortsätta realisera instruktionen. Kort sagt, vi får en vild adressering under ett tryck på SW2 men sedan kommer adressen vanligtvis vara ok under flera tryck. Detta innebär att när man ser att adressen stabiliserats så är den riktig. Ta t.ex en sådan instruktion som ORA $ som tar 15 klockcykler för våran fantastiska CPU. När den håller på att sätta upp extended-adressen har vi ett kortvarigt problem (HB först, LB sen). Sedan stabiliseras dock adressbussen för varje tryck på SW2 för då realiseras instruktionen och PC står still.

Vi börjar med att programmera resetvektorn till att vara $8000 dvs precis där PROM-arean börjar. På $FFFE programmerar vi alltså $80 och på $FFFF programmerar vi $00. När så spänningen till vår CPU slås på kommer adressen att bli $FFFE. Därefter har vi SW2 till vårt förfogande. Vi trycker alltså på SW2 tills dess vi får $8000 ut på adressbussen. Där har vi sedan vår första OP-kod (dvs programmet börjar). Säg att den är OP-koden för LDA $ ($C6). På $8001 har vi sedan $40, på $8002 har vi $00. Detta för att vi vill adressera vår testrigg med LDA $4000. CPU'n kommer då ladda in vårt iställda värde i ackumulatorn. Om vi på rad $8003 sedan har OP-koden för ORA # (dvs $AA) och säg $01 på rad $8004 så kommer värdet vi ställer in OR'as med $01. Om vi till exempel ställer in $02 så kommer värdet som återskrivs till ackumulatorn bli $03. Vi kan med vår fantastiska testrigg testa detta genom att göra en STA $4000 dvs $C7 på rad $8005, $40 på rad $8006 och $00 på rad $8007. Ut på testriggen ska vi alltså få $03.

Vi ska nu försöka skriva ett program som testar alla våra 35 instruktioner i enlighet med kapitlet CPU Mnemonics ovan.

Vi fortsätter enligt inledningen med startadress $8000. Ett testprogram kan då se ut (och vi har då lagt till funktionen med adresser för varje instruktion vilket i praktiken inte görs då programmet skall kunna läggas på valfritt ställe i minnet. Vi har här emellertid av pedagogiska skäl valt att specificera absolutadresser som alltså normalt görs mha den så kallade länkaren).

$8000 LDA #$FE
$8002 ADD #$02
$8004 ADC #$00
$8006 STA $4000 //ska bli $01 ut från IC3
$8009 LDA $4000 //ställ in $FE mha BCD-omk
$800C ADD $4000 //ställ in $02 mha BCD-omk
$800F ADC $4000 //ställ in $00 mha BCD-omk
$8012 STA $4000 //ska bli $01 ut från IC3
$8015 LDA #$FE
$8017 DECA
$8018 CMP #$FC
$801A BNE $FD //(-3)
$801C STA $4000 //ska bli $FD ut från IC3
$801F INCA
$8020 CMP $4000 //sätt $FF
$8023 BNE $FC //(-4)
$8025 CMP #$FF
$8027 BEQ $01
$8029 LDA #$00
$802B CMP #$01
$802D BMI $01
$802F LDA #$02
$8031 CMP #$01
$8033 BPL $01
$8035 LDA #$01
$8037 EOR #$F0
$8039 STA $4000 //ska bli $F1
$803C EOR $4000 //ställ in $01
$803F STA $4000 //ska bli $F0
$8042 JSR $9000 //här har vi en subrutin
$8045 LDA #$02
$8047 LSRA
$8048 STA $4000 //här ska vi ha $01
$804B LSLA
$804C STA $4000 //här ska vi ha $02 igen
$804F LDA #$00
$8051 NEGA
$8052 STA $4000 //här ska vi ha $FF
$8055 NOP //här ska inget ske
$8056 LDA #$F2
$8058 ORA #$F3
$805A STA $4000 //här ska vi ha $F3
$805D ORA $4000 //ställ in $F4
$8060 STA $4000 //här ska vi ha $F7
$8061 PSHA
$8062 PULA
$8063 STA $4000 //här ska vi återigen ha $F7
$8066 STA $4000 //här ska vi ha $F6
$8069 SUB $4000 //ställ in $01
$806C STA $4000 //här ska vi ha $F5
$806F LDA #$01
$8071 ADD #$01
$8073 TPA
$8074 STA $4000 //här ska C, V, Z, N och H vara noll (dvs b7-b3)
$8077 LDS #1FFF //sätter SP
$807A LDA #$FF $807C PSHA
$807D PULA
$807E STA $4000 //checkar stackvärde som ska vara $FF
$8081 NOTA
$8082 STA $4000 //ska vara $00
$8085 JMP $8000 //dvs börja om

$9000 RTS //på denna adress programmerar vi tillfälligtvis bara OP-koden för RTS

$FFFE $80
$FFFF $00 //här programmerar vi alltså resetvektorn dvs där programmet börjar

Nåt sånt här kan vi göra.

Här specificerar vi vad som ska hända rad för rad i programminnet. Vi nyttjar ren hexkod (alltså inga fler dollar-tecken) och kommenterar bort Mnemonics men har dom kvar enbart för att ha koll på vad det är vi för tillfället gör.

8000 A6 //LDA #
8001 FE
8002 AB //ADD #
8003 02
8004 A9 //ADC #
8005 00
8006 C7 //STA $
8007 40
8008 00 //ska bli $01 ut från IC3
8009 C6 //LDA $
800A 40
800B 00 //ställ in $FE mha BCD-omk
800C CB //ADD $
800D 40
800E 00 //ställ in $02 mha BCD-omk
800F C9 //ADC $
8010 40
8011 00 //ställ in $00 mha BCD-omk
8012 C7 //STA $
8013 40
8014 00 //ska bli $01 ut från IC3
8015 A6 //LDA #
8016 FE
8017 4A //DECA
8018 A1 //CMP #
8019 FC
801A 26 //BNE
801B FC //(-4)
801C C7 //STA $
801D 40
801E 00 //ska bli $FC ut från IC3
801F 4C //INCA
8020 C1 //CMP $
8021 40
8022 00 //sätt $FF
8023 26 //BNE
8024 FB //(-5)
8025 A1 CMP #
8026 FF
8027 27 //BEQ
8028 01
8029 A6 //LDA #
802A 00
802B A1 //CMP #
802C 01
802D 2B //BMI
802E 01
802F A6 //LDA #
8030 02
8031 A1 //CMP #
8032 01
8033 2A //BPL
8034 01
8035 A6 //LDA #
8036 01
8037 A8 //EOR #
8038 F0
8039 C7 //STA $
803A 40
803B 00 //ska bli $F1
803C C8 //EOR $
803D 40
803E 00 //ställ in $01
803F C7 //STA $
8040 40
8041 00 //ska bli $F0
8042 CD //JSR $
8043 90
8044 00 //här har vi en subrutin
8045 A6 //LDA #
8046 02
8047 44 //LSRA
8048 C7 //STA $
8049 40
804A 00 //här ska vi ha $01
804B 48 //LSLA
804C C7 //STA $
804D 40
804E 00 //här ska vi ha $02 igen
804F A6 //LDA #
8050 00
8051 40 //NEGA
8052 C7 //STA $
8053 40
8054 00 //här ska vi ha $FF
8055 9D //NOP //här ska inget ske
8056 A6 //LDA #
8057 F2
8058 AA //ORA #
8059 F3
805A C7 //STA $
805B 40
805C 00 //här ska vi ha $F3
805D CA //ORA $
805E 40
805F 00 //ställ in $F4
8060 C7 //STA $
8061 40
8062 00 //här ska vi ha $F7
8061 87 //PSHA
8062 86 //PULA
8063 C7 //STA $
8064 40
8065 00 //här ska vi återigen ha $F7
8066 C7 //STA $
8067 40
8068 00 //här ska vi ha $F6
8069 C0 //SUB $
806A 40
806B 00 //ställ in $01
806C C7 //STA $
806D 40
806E 00 //här ska vi ha $F5
806F A6 //LDA #
8070 01
8071 AB //ADD #
8072 01
8073 85 //TPA
8074 C7 //STA $
8075 40
8076 00 //här ska C, V, Z, N och H vara noll (dvs b7-b3)
8077 45 //LDS #
8078 1F
8079 FF //sätter SP
807A A6 //LDA #
807B FF
807C 87 //PSHA
807D 86 //PULA
807E C7 //STA $
807F 40
8080 00 //checkar stackvärde som ska vara $FF
8081 9C //NOTA
8082 C7 //STA $
8083 40
8084 00 //ska vara $00
8085 CC //JMP $
8086 80
8087 00 //dvs börja om

9000 81 //RTS, på denna adress programmerar vi tillfälligtvis bara OP-koden för RTS

FFFE 80
FFFF 00 //här programmerar vi alltså resetvektorn dvs där programmet börjar

Här listar vi ovanstående program på det sättet som en gammal hederlig PROM-brännare kan förstå. Den tar alltså åtta byte med data per listad adress. Så här kommer det alltså se ut:

8000 A6 FE AB 02 A9 00 C7 40
8008 00 C6 40 00 CB 40 00 C9
8010 40 00 C7 40 00 A6 FE 4A
8018 A1 FC 26 FD C7 40 00 4C
8020 C1 40 00 26 FC A1 FF 27
8028 01 A6 00 A1 01 2B 01 A6
8030 02 A1 01 2A 01 A6 01 C7
8038 F0 C7 40 00 C8 40 00 C7
8040 40 00 CD 90 00 A6 02 44
8048 C7 40 00 48 C7 40 00 A6
8050 00 40 C7 40 00 9D A6 F2
8058 AA F3 C7 40 00 CA 40 00
8060 C7 40 86 C7 40 00 C7 40
8068 00 C0 40 00 C7 40 00 A6
8070 01 AB 01 85 C7 40 00 45
8078 1F FF A6 FF 87 86 C7 40
8080 00 9C C7 40 00 CC 80 00

9000 81 FF FF FF FF FF FF FF

FFF8 FF FF FF FF FF FF 80 00

Data i oprogrammerade adresser är normalt idel ettor dvs FF. Detta får genomslag vid assembleringen av 9001+ och adresserna före FFFE.

Här ska vi skriva ett litet program som är tänkt att testa om pollingen hos vår processor verkligen fungerar. Man byter lämpligen ut den manuella klockan mot en astabil multivibrator på säg 50Hz. Programmet kan se ut som följer:

start: LDA $4000 //ställ in lite olika värden och till slut $01
CMP #$01
BNE start //-7, F9
STA $4000 //skriver $01 till testrigg
loop: LDA $4000 //ställ in lite olika värden och till slut $02
CMP #$02
BNE loop //-7, F9
STA $4000 //skriver $02 till testrigg
JMP start

Här har vi mer anammat riktig assembler-syntax med så kallade labels (typ start) istället för absoluta adresser eller offsets. Nedan följer av kuriosaskäl en HCS08-variant som man alltså kan skriva rätt i C-kompilatorn.

_asm("start: LDA $4000"); //ställ in lite olika värden och till slut $01
_asm("CMP #$01");
_asm("BNE start");
_asm("STA $4000"); //skriver $01 till testrigg
_asm("loop: LDA $4000"); //ställ in lite olika värden och till slut $02
_asm("CMP #$02");
_asm("BNE loop");
_asm("STA $4000"); //skriver $02 till testrigg
_asm("JMP start");

Det lär finnas ett smidigare sätt att skriva assembleringskommandorna på (och inte _asm för varje rad) men författaren har inte lyckats komma på det. Ovanstående fungerar dock men blir naturligtvis jobbigt för stora program.

Vi bestämmer oss för att minnesmappa även ovanstående program. Tyvärr kan vi inte bara addera programmet till det andra programmet - då det kräver en annan resetvektor - även om vi faktiskt skulle kunna skriva det som en subrutin men det stämmer då inte med den manuella klockan och blir struligt. Vi får helt enkelt programmera om vårt minne (men vi leker med tanken att det ska bli en subrutin ändå och lägger då programmet på adress $9000 för det är dit vårt testprogram hoppar. Dock kan vi då inte använda JMP i subrutinen för då fastnar testprogrammet där. Vi kan dock skapa en räknare som kör ett begränsat antal varv). Den utvecklade subrutinen skulle kunna se ut:

LDA #$0A //vår räknare
PSHA //eftersom vi bara har en ackumulator måste räknarvärdet pushas undan på stacken
start: LDA $4000 //ställ in lite olika värden och till slut $01
CMP #$01
BNE start
STA $4000 //skriver $01 till testrigg
loop: LDA $4000 //ställ in lite olika värden och till slut $02
CMP #$02
BNE loop
STA $4000 //skriver $02 till testrigg
PULA //här hämtar vi aktuellt räknarvärde
DECA
CMP #$00
BEQ end
PSHA //pushar återigen undan aktuellt räknarvärde
JMP start
end: RTS

Minnesmappningen av vårt enklare pollingprogram blir:

9000 C6 //LDA $
9001 40
9002 00
9003 A1 //CMP #
9004 01
9005 26 //BNE
9006 F9
9007 C7 //STA $
9008 40
9009 00
900A C6 //LDA $
900B 40
900C 00
900D A1 //CMP #
900E 02
900F 26 //BNE
9010 F9
9011 C7 //STA $
9012 40
9013 00
9014 CC //JMP $
9015 90
9016 00

Och på brännbart maskinkodsformat blir det:

9000 C6 40 00 A1 01 26 F9 C7
9008 40 00 C6 40 00 A1 02 26
9010 F9 C7 40 00 CC 90 00 FF

FFF8 FF FF FF FF FF FF 90 00

Detta avsnitt behandlar de ingående CPU-komponenternas realisering.

Figuren visar vald registerrealisering. Detta hade kunnat göras enklare med ett gäng D-vippor, och enablesignalerna från IR direkt som CP, men vi får då garanterat problem med timingen. Med vidstående registertyp hinner vi enabla signalerna innan CP kommer. Detta går tyvärr inte med D-vippor allena. LD_DIR, LD_CCR, LD_FA, LD_AND, LD_OR, LD_XOR, LD_IRR, LD_BR, LD_PC_HB, LD_PC_LB, LD_AR_HB och LD_AR_LB är alla styrsignaler till register av denna typ. Eftersom SR=00 håller informationen så är informationen kvart i vipporna när LD är låg.

Bilden visar en paralellt laddningsbar upp/ned-räknare. Denna räknare avses användas både som stackpekarregister (SP), IR-räknare (IRC) och programräknare (PC). I fallet PC och IRC kommer den dock hårdkodas till att bara kunna räkna uppåt (U/D'=1).

Bilden visar ett paralellt laddningsbart skiftregister. Vi använder två stycken i vår CPU. En för högerskift (LSR) och en för vänsterskift (LSL) (det samlade namnet på dessa är ackumulator A). Om vi använder konventionen att MSB (b7) är längst till vänster så kan vi applicera databussen med b7 längst till vänster hos det register som ska skifta åt höger (LSR). När vi sedan ska skifta åt vänster permuterar vi databussen så att b7 hamnar längst till höger varvid vi gör ett högerskift igen men som då motsvaras av ett vänsterskift. Det är viktigt att permutera tillbaks bussen på utgående sida av skiftregistret. Man kan också välja att helt enkelt fysiskt vända skiftregistret som ska skifta åt vänster. Insignalen x är hårdkodad till 0 för vi avser bara kunna dividera respektive multiplicera med multiplar om två.

Bilden visar heladderarens (FA) realisering för en bit. För alla åtta bitar kopplar man bara åtta stycken celler i rad. Heladderaren tar två tal in, xi och yi. Förutom detta tar den hänsyn till om carry genererats i närmast föregående position dvs ci. Ut kommer summan si samt eventuell carry till nästkommande position, ci-1. Konventionen bygger på att MSB har lägst nummer men så är inte fallet för oss. Det är bara av bekvämlighetsskäl som detta används här. För en mer detaljerad beskrivning av en adderare se artikeln Digitalteknik eller Adderare i Wikipedia.

Detta avsnitt behandlar tänkbara realiseringar av alla typer av grindar. Realiseringarna är av pedagogiska skäl gjorda med bipolära transistorer. Moderna digitala kretsar innehåller dock mest MOSFET's (Metal Oxide Semiconductor Field Effect Transistor).

Bilden visar en bipolär transistor av NPN-typ. Det finns även en komplementär variant som kallas PNP där strömmarna går åt direkt motsatt riktning men den används sällan i digitala grindar så vi nöjer oss med att visa NPN-varianten. Transistorn består av tre ben. Dessa är Bas (B), Kollektor (C) och Emitter (E). När transistorn tillförs en ström på basen får man en i regel mycket högre ström på kollektorn. Denna förstärkningsfaktor kallas för Beta (Ic är alltså Beta gånger större än Ib). Beta varierar med både kollektorström, kollektor-emitterspänning och temperatur så den är långt ifrån konstant men brukar för små signaler anses vara konstant. I digitala sammanhang är vi dock mest intresserade av dess switchegenskaper dvs vad som krävs för av (strypt) eller på (bottnad). Så betafaktorn får en underårdnad betydelse. För småsignaltransistorer kan man räkna med en betafaktor på mer än 100. Vi har med andra ord att räkna med en tämligen stor betafaktor. Nånting som är bra att tänka på är att en transistor av kiseltyp behöver minst typ 0.7V över bas-emittersträckan för att överhuvudtaget kunna leda någon ström. I övrigt kommer vi åtminstone preliminärt inte gå in mer på hur denna fantastiska manick fysiskt fungerar och är uppbyggd. Det ska bara konstateras att det var en revolution, åtminstone storleksmässigt, när den kom (1947) och så småningom nästan tog död på röreran.

Bilden visar den enklaste formen av grind dvs en inverterare. Vi skickar alltså in en signal (x) och får inversen (x') ut. Detta beror på att vi i det höga fallet förser den med så pass mycket basström att transistorn bottnar (0). Från transistoravsnittet ovan har vi ju att räkna med en betafaktor på mer än 100 vilket innebär att det hade räckt med 100k på ingången för att få transistorn att bottna. När vi sedan skickar in en låg signal får transistorn ingen ström alls varvid den blir strypt (1). Valet av 1k kollektormotstånd ger en kanske onödigt hög ström (5mA) vid låg utnivå men det har mest valts av pedagogiska skäl. Både sanningstabellen och grindsymbolen visas till höger.

Av kuriosaskäl kan nämnas att vald realisering av inverterare inte kommer att vara överdrivet snabb. Detta beror på Miller-effekten dvs den multiplicering av kapacitansen mellan kollektor och bas (Cbc) som sker när man har stor förstärkning hos en transkonduktiv komponent. Om författaren minns rätt så kan denna överskottsladdning ledas bort med hjälp av en diod mellan bas och kollektor. Ett annat sätt att snabba på switchningen är en liten kondensator över basmotståndet. Men vi är inte intresserade av snabba datorer här.

Bilden visar en NAND-grind. Denna grind är låg när alla ingångar är höga men hög annars. Ingångstransistorerna är kopplade på ett lite speciellt sätt. Dom får sin basström från det gemensamma basmotståndet på 10k. Så fort minst en av ingångarna går låg så får vi de facto en kortslutning av bas-emittersträckan hos utgångstransistorn. Utgångstransistorn stryps då och vi får hög signal ut. Både sanningstabell och grindsymbol syns till höger.

Bilden visar en OR-grind. Denna grind är hög när minst en av ingångarna är höga och låg annars. Både sanningstabell och grindsymbol syns till höger. Symbolen >1 är inte helt riktig då det borde vara >=1 (för man kan se ingångarna som en binär summering) men det blir rittekniskt klumpigt.

Bilden visar en AND-grind. Denna grind är hög när alla ingångarna är höga och låg annars. Vi har här valt att helt enkelt hänga på en inverterare av ovanstående typ. Detta är med andra ord ingen direkt fundamental grind för den kan byggas av de andra tre ovan. Både sanningstabell och grindsymbol syns till höger.

Bilden visar en NOR-grind. Denna grind är hög när alla ingångarna är låga och hög annars. Vi har här valt att helt enkelt hänga på en inverterare av ovanstående typ. Detta är med andra ord ingen direkt fundamental grind för den kan byggas av de andra tre ovan. Både sanningstabell och grindsymbol syns till höger.

Bilden visar en XOR-grind. Denna grind är hög när ena ingången är hög (och den andra låg) och låg annars. Vi har här valt att realisera grinden med redan befintliga grindar enligt ovan. Det vore lite spännande att se en diskret version. Man kan naturligtvis även här hänga på en inverterare. Man får då en s.k XNOR-grind (som indikerar likhet). Både sanningstabell och grindsymbol syns till höger.

Bilden visar en three-state-grind. Denna, något oegentligt kallad grind, är, liksom inverteraren, hög när ingången är låg och vice versa (signalen OE måste dock i det här fallet vara hög). För att realisera en icke-inverterande three-state-grind kan man helt enkelt montera en inverterare före grinden. Båda typerna har ett tredje tillstånd dvs högimpediv (OE=0). I detta tillstånd kan man applicera en signal direkt på utgången. Detta krävs när man har att göra med buss-baserade system såsom i en processor. Om man lite grovt ska försökas förklara funktionen så har vi först och främst att när OE=1 och ingången är hög så leder T2. Därmed leder T3 och vi får låg signal ut. När insignalen är låg spärrar T2 och T3 varvid vi får hög signal ut. Om nu OE=0 kommer alla tre transistorerna att spärra och vi får hög impedans ut. Den allmänna symbolen är en triangel med en pinne (OE) på. Triangeln som finns med i figuren är ett annat sätt att rita en inverterare. Vanligtvis av så kallad Schmitt-trigger typ.

Vidstående bild visar ett par sätt att generera spikar eller hasarder beroende på vilken flanktyp man vill ska vara aktiv (detta används i flanktriggade vippor). Spikbildningen genereras på grund av den fördröjning (grindfördröjning) som alltid finns hos digitala kretsar. Bilden till vänster genererar således en spik då insignalen går hög. Detta för att NAND-grinden är hög när ingångarna är låga. Men när ingången sen går hög så tar det en pytteliten stund innan inverteraren (som här har gestaltats med hjälp av en en NAND-grind med kortslutna ingångar) går låg. Under denna lilla stund är således båda ingångarna höga vilket får till följd att utgången blir kortvarigt låg. Denna spik är av storleksordningen nanosekunder och det kan hända att detta inte räcker för att t.ex nollställa en räknare. Man kan då prova att montera en liten kondensator på utgången av inverteraren för att ytterligare slöa ner den och därmed få en kraftigare spik. Alternativt kan man koppla flera (udda antal) inverterare i serie.

I detta avsnitt behandlas en serie speciellt användbara minneselement eller så kallade vippor och hur dom är realiserade och kan användas. Den allra enklaste formen av vippa är SR-vippan.

Bilden visar ett par korskopplade NAND-grindar. Dessa utgör en minnescell i form av en SR-vippa (observera att ingångarna är inverterade). Antag att SW står i läge nedåt. Q' kommer då garanterat vara hög (då NAND står för NOT AND och alltså bara är låg när båda ingångarna är höga) och Q kommer vara låg då båda dess ingångar är höga. När sedan SW byter läge kommer Q' genast gå låg samtidigt som Q går hög. När SW är i luften behålls nämligen det tidigare värdet (pga att S'R'=11) och tillståndsbytet sker bara en gång. Detta gör att kontaktstudsar elimineras.

Denna koppling är mycket effektiv när man vill koppla in brytare till processorer. Man slipper alltså filter och/eller speciella rutiner för att mjukvarumässigt filtrera en insignal. Nackdelen är att brytaren måste ha två lägen så det fungerar alltså inte med vanliga tryckknappar.

Bilden visar arkitekturen hos en flanktriggad D-vippa (se spikbildare ovan). Varje gång klockpulsen CP (eng. Clock Pulse) går hög överförs värdet på ingången D till utgången Q. D-vippan består i grund och botten av en ännu enklare vippa. Om man tar bort inverteraren som går från D till den övre grinden och kallar den övre signalen för R (som i Reset) och byter ut D mot S (som i Set) får man nämligen en så kallad SR-vippa. Detta är den allra enklaste formen av (synkront) minneselement i digitala kretsar. 74HC74 är en flanktriggad (positiv flank) D-vippa.

Bilden visar en flanktriggad D-vippa med asynkron Preset och Reset. Man kan alltså godtyckligt tippa vippan åt endera hållet med hjälp av signalerna R' och P'. Dessa är aktivt låga och måste släppas höga innan nytt tillståndsbyte hos vippan kan ske.

Bilden visar en SR-vippa med tillhörande sanningstabell. SR-vippan är en förenklad version av D-vippan. Dess sanningstabell visas till höger. Sanningstabellen skall tolkas som så att värdena i tabellen är de värden vippan antar som "nästa" värde, alltså vid nästkommande aktiv klockflank. Ingångsvärdet SR=11 är inte tillåtet (för då är vippan ej definierad).

Bilden visar en D-vippa med tillhörande sanningstabell. D-vippan är en utvidgad version av SR-vippan. Dess sanningstabell visas till höger. Sanningstabellen skall tolkas som så att värdena i tabellen är de värden vippan antar som "nästa" värde, alltså vid nästkommande aktiv klockflank.

Bilden visar en JK-vippa med tillhörande sanningstabell. JK-vippan är en utvidgad version av SR-vippan som involverar återkoppling. Dess sanningstabell visas till höger. Sanningstabellen skall tolkas som så att värdena i tabellen är de värden vippan antar som "nästa" värde, alltså vid nästkommande aktiv klockflank. JK-vippan har den fördelen över SR-vippan att den är definierad för alla typer av insignalskombinationer. Förutom att data togglar (dvs skiftar värde) för varje klockpuls när JK=11 så skiljer sig inte JK-vippan och SR-vippan sig åt. Det är exakt samma typ av minnescell.

Bilden visar en T-vippa byggd kring en SR-vippa. Det går naturligtvis att bygga en T-vippa av en D-vippa också men den blir onödigt komplex. T-vippan skiljer sig från frekvenshalveraren i det enda avseendet att togglandet är på och avstängningsbart med hjälp av styrsignalen T. Denna styrsignal består i sin tur egentligen av kortslutna ingångar hos en så kallad JK-vippa.

Bilden visar en frekvenshalverare byggd kring en D-vippa. Denna vippa byter tillstånd varje gång klockan (CP) går hög (eller låg beroende på flanktriggningen hos D-vippan vilken dock brukar vara positiv). Frekvenshalveraren är med andra ord en specialvariant av D-vippa där den inverterande utgången Q' har återkopplats till ingången. Detta får till följd att det krävs två flanker för att vippan ska gå från hög till låg. Därav frekvenshalveringen.

Bilden visar strukturen hos en RAM-minnescell. En enda bits information i ett vanligt RAM-minne lagras alltså med hjälp av en vanlig vippa (i det här fallet en typ av D-vippa). Detta får till följd att minnet blir väldigt snabbt. Samtidigt tappar det emellertid sin information vid spänningsbortfall. Minnet fungerar på så sätt att det adresseras via Adress varvid data läses om R/W' (Read/Write) är hög eller skrivs om R/W' är låg. Hela minnescellen är egentligen inte visad. Vi behöver en eller ett par three-state-grindar då data in och data ut delar på samma buss.

Nedanstående är så kallade binärräknare (0-F) men räknare kan naturligtvis fås att räkna på annat sätt också. Dekadräknare (0-9) är t.ex vanliga. Pseudo-slumpräknare i form av ringräknare finns också. Men vi går inte in på dessa här.

Bilden visar en asynkron binärräknare som också kallas ripple-carry räknare. Enligt ovan vet vi att utgångarna växlar tillstånd varje gång CP går hög. Om man som i bilden kopplar utgångarna som klocka till nästkommande krets kommer varje utgång räkna binärt ett steg högerjusterat. Q1 räknar alltså minst signifikant och Q4 mest signifikant i just denna nibbel. 74HC191 är en 4-bit Binary Up/Down Counter.

Till skillnad från den asynkrona räknaren ovan är denna räknare synkron med klockpulsen CP dvs den byter tillstånd exakt i takt med CP. Detta är en förutsättning för att räknaren ska kunna ingå i sekvensiella nät såsom i en CPU. Räknaren utgörs av en serie T-vippor som fungerar som frekvenshalverare med tillägget att T måste vara hög för att tillståndsförändring skall kunna ske.

Register används flitigt i digitala sammanhang. Inte minst i processorer. Vi listar här dom två grundtyperna. Med register mellanlagrar man alltså data mha av klockade vippor enligt ovan. Man kan kombinera dom båda så att man får ett paralellt laddningsbart skiftregister. Vår ackumulator är av denna typ.

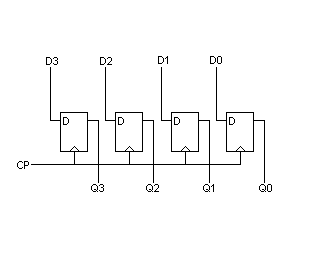
Bilden visar enklast tänkbara register. Registret består alltså bara av ett antal D-vippor. Varje gång CP (eller en enable-signal) går hög överförs data (D0-D3) till utgångarna (Q0-Q3).

Bilden visar ett enkelt skiftregister. Dess huvuduppgift är att ta emot data seriellt och konvertera det till paralell form. I det här fallet klockas LSB in först.

Bilden visar en monostabil multivibrator. Ordet mono betyder en och avser här att den endast har ett stabilt tillstånd. Eftersom kretsen ofta även har en inverterande utgång, Q', så är det svårt att säga vilket tillstånd som är det stabila men normalt brukar man säga att det normala tillståndet är låg medan det aktiva tillståndet är hög. Just denna krets triggas av negativ flank på B' varefter Q går hög under:

${\displaystyle T=0,72RC\ }$ sekunder

vilket naturligtvis bara gäller för angiven krets men principen är densamma oavsett krets.

En astabil multivibrator med grindar kan konstrueras med tre olika typer av grindar (bara alla ingångar är ihopdragna). Dessa är NAND (Not AND), NOR (Not OR) eller inverterare (NOT).

Denna krets fungerar tyvärr endast med CMOS-kretsar ur exempelvis 74HC-serien eller 4000-serien. Detta för att drivning av TTL-ingångar kräver att den drivande enheten kan sänka ström (se TTL).

Man kan visa att frekvensen blir:

${\displaystyle f_{0}={\frac {1}{2RC\ln {3}}}}$ Hertz

Bilden visar en multiplexers arkitektur. Ringarna representerar inverterare, & betyder AND-grind och >1 betyder OR-grind. Med hjälp av styrsignalen ABC kan man alltså välja vilken av dom åtta ingångarna som ska vara aktiv. Om styrsignalen ABC alltså till exempel är 110 binärt är ingång 6 aktiv osv. 74HC251 är en 8 Channel Multiplexer.

Bilden visar en avkodares (eng. demultiplexer) arkitektur. Den är uppbyggd kring ett antal AND-grindar och ett antal inverterare (representerade av ringarna). Avkodaren realiserar alltså alla tänkbara kombinationer av insignalen. Om ABC till exempel är 011 blir alltså AND-grind nummer 3 aktivt hög osv. 74HC138 är en 3-To-8 Line Decoder.

Ackumulator kallas den delen av en processor där resultat från ALU'n mellanlagras och manipuleras (främst skiftas eller jämförs). Multiplikation och division med multiplar om två är möjlig genom vänster respektive högerskift.

Termen ackumulator betydde ursprungligen en enhet som kombinerade funktionen av tallagring och addition. Ett tal som överfördes till ackumulatorn adderades automatiskt med dess föregående värde. Räknarhjulsminnen hos tidiga mekaniska datorer hade ackumulatorer av denna typ.

Bilden visar enklast tänkbara register. Registret består alltså bara av ett antal D-vippor. Signalen CP behöver inte vara diskontinuerligt varierande. Den kan också vara en enable-signal ut från exempelvis instruktionsregistret. I det fallet får vi dock problem med synkronismen varför vi ändå valt att klocka våra register med CP med tillägget av paralell load-signal (LD). Bilden är repeterad här för att den är en av grundbyggstenarna i ackumulatorn.

Bilden visar ett enkelt skiftregister. Dess huvuduppgift är att ta emot data seriellt och konvertera det till paralell form. I det här fallet klockas LSB in först. Bilden är repeterad här för att den är en av grundbyggstenarna i ackumulatorn.

Bilden visar ett något mer avancerat skiftregister än basic skiftregister. Detta skiftregister kan laddas parallellt och skicka data seriellt och det kan även laddas seriellt och skicka data parallellt. Vi närmar oss med andra ord en ackumulator.

Signalen Xin laddar vipporna parallellt med X1-X4, x är seriell data in och SV står för Skift Villkor och är aktivt hög för högerskift.

Bilden visar en tänkbar realisering av en ackumulator. Ackumulatorn består egentligen av två ackumulatorer (eller speciella skiftregister). Detta för att skiftning ska kunna göras åt båda hållen. Data skyfflas alltså fram och tillbaks mellan Ackumulator A och Ackumulator B när skift åt olika håll måste göras. Data läggs då ut på databussen och pga att flera (interna) enheter delar på databussen så måste så kallade three-state buffrar (B1 och B2) användas. Dessa är alltså högimpediva när de inte används (EnA=EnB=0). Detta för att undvika kortslutning när andra enheter vill låna bussen. Insignalerna har bytt namn men torde vara lätta att identifiera om man jämför med skiftregistret ovan.

Behovet att jämföra två tal är vanligt förekommande i all digitalteknik. Om vi antar att X=<x1, x2,...,xn> och Y=<y1, y2,...yn> är givna kan önskemålet antingen vara att indikera fallet X=Y eller att indikera något av fallen X>=Y, X>Y, X<=Y eller X<Y. Vi noterar att påståendet X>=Y är negationen till X<Y och om vidare variablerna permuteras övergår X>=Y i påståendet X<=Y och X<Y övergår i X>Y. Av detta resonemang framgår att man vid realisering av en komparator bara har att skilja på två fall:

${\displaystyle X=Y}$

och

${\displaystyle X<Y}$

Bilden visar en basic komparator för xi=yi realiserad av en XOR-grind och en inverterare. Att det blir så enkelt är lätt att inse om man studerar sanningstabellen för en XOR-grind då den ju ger ett ut när signalerna är olika och således noll när signalerna är lika. Därav inverteraren.

Bilden visar en 4-bitars realisering av en komparator för X=Y. Om någon bitposition är olika genererar alltså XOR-grinden, enligt ovan, hög signal ut. När man jämför hela tal räcker det alltså att kontrollera om någon XOR-grind har gått hög då detta indikerar olikhet. För man in den signalen på en OR-grind kommer den att gå hög så fort det är en olikhet i någon position och alltså indikera olikhet. Inverterar man sedan denna signal med hjälp av en inverterare (varvid man får en NOR-grind) kommer utsignalen alltså i stället indikera likhet dvs X=Y.

Bilden visar en komparator för X<Y. Realiseringen skulle kunna vara borrow-kedjan i en subtraherare men vi har här valt en annan princip. Vi börjar alltså med den mest signifikanta positionen MSB och konstaterar att om x1'y1=1 så gäller omedelbart att X<Y. Om dessutom w2=x1'+y1=1 (dvs de tre fallen x1y1=00, 01 eller 11) och x2'y2=1 har vi också X<Y. Wi=1 betyder alltså att även nästa position måste kollas om xi<yi eller ej.

ALU står för Arithmetic Logic Unit och är den delen i en processor som utför aritmetiska beräkningar och då speciellt addition och subtraktion samt logiska operationer. Multiplikation och division sker normalt genom en serie additioner och subtraktioner. Ibland hårdkodas dock multiplicerare för att snabba upp processen (men vi är inte intresserade av snabba datorer här).

Bilden visar en basic adderare i form av en enda XOR-grind. En addition av två tal bestående av en bit vardera är alltså mer eller mindre komplett efter att ha passerat en XOR-grind. Två saker saknas dock. Det ena är genereringen av carry dvs ett slags overflow som inträffar när båda bitarna är höga. Denna generering utföres av en halvaddderare som är en basic adderare med en AND-grind som jobbar på dom ingående bitarna. Detta förstås lätt om man betänker att 1+1=0 med 1 som carry till nästa position. En heladderare tar även hänsyn till om det har genererats carry från föregående bitars addition och vidarbefordrar denna eventuella etta till nästa cell.

Bilden visar en heladderares bakomvarande teori och realisering. I a) visas hur minnesiffran kallad carry genereras både decimalt och binärt. En heladderare tar alltså hänsyn till om carry har genererats i högre position eller ej. I b) summeras helt enkelt carry med dom båda bitarna xi och yi. Övriga kombinationer visas i sanningstabellen i c) varvid vi får Karnaughdiagrammen i d). Ur Karnaughdiagrammen får vi sedan:

${\displaystyle s_{i}=c_{i}'x_{i}'y_{i}+c_{i}'x_{i}y_{i}'+c_{i}x_{i}'y_{i}'+c_{i}x_{i}y_{i}=c_{i}\oplus x_{i}\oplus y_{i}}$

och

${\displaystyle c_{i-1}=x_{i}y_{i}+c_{i}y_{i}+c_{i}x_{i}=x_{i}y_{i}+c_{i}(x_{i}\oplus y_{i})}$

vilket realiseras av grindarna i e). Den kompletta adderaren byggs sedan upp av en kedja av ovanstående struktur i f) kallade FA (från engelskans Full Adder).

Intresserade bör läsa artikeln adderare i Wikipedia.

Bilden visar en helsubtraherares bakomvarande teori och realisering. Talen antas positiva och representerade enligt

Y=<y1, y2,...,yn>

och

X=<x1, x2,...,xn>

där Y alltså subtraheras från X (D=X-Y).

I a) har vi använt den klassiska metoden med "lån" som markeras med ett streck över den siffra som är lånegivare. I de fall där närmast högre position i X är 0 fortplantar sig lånebehovet tills en 1:a påträffas som genom successiva lån överbringar en 2:a till den behövande positionen.

I b) har vi infört en ny rad för lånesiffrorna bi där bi=1 betyder lån från position i krävs av närmast lägre position i+1. För varje position ska vi sedan generera dels differenssiffran di dels eventuell borrow bi-1 (=lånekrav) till närmast högre position. Vid bildandet av differenssiffran gäller att xi har vikten +1, yi har vikten -1 och bi har vikten -1. Skulle det inträffa att denna summering blir <0 tar vi för givet att ett lån uttages av närmast högre position, dvs vi noterar bi-1=1 och underförstår samtidigt att aktuella positionen får ett tillskott av två.

Funktionstabellen får utseendet enligt c), Karnaughdiagrammet för di och bi-1 enligt d). Byggstenen i en subtraherare, i e) betecknad FS, kan alltså ges samma struktur som en heladderare (FA):

${\displaystyle d_{i}=x_{i}\oplus y_{i}\oplus d_{i}}$

och

${\displaystyle b_{i-1}=x_{i}'y_{i}+b_{i}(x_{i}\oplus y_{i})'}$

Funktionen di kan ges exakt samma form som summan si vid addition medan bi-1 överensstämmer med ci-1 om xi utbytes mot xi' (se respektive Karnaughdiagram).

En sak återstår: tolkningen av b0. Om X>=Y är uppenbarligen b0=0. Omvänt indikerar b0=1 att X<Y. Tyvärr är differensen D=<d1,d2,...,dn> i detta speciella fall inte en beloppsangivelse av |X-Y| som kanske vore önskvärt utan det så kallade två-komplementet av differensens belopp. I de flesta datorer utförs därför inte subtraktion av en speciell subtraherare utan med en adderare och komplementerande nät. Detta möjliggörs genom representation av negativa tal med komplement såsom 2-komplement.

En CPU måste ha någon form av ett litet icke-flyktigt minne där den kan hämta basala instruktioner (instruktionsregister). Detta behöver dock inte vara programmerbart mer än en gång så man kan tänka sig att dom små instruktionsprogrammen hårdkodas i det enklaste RISC-fallet, vilket vi i princip också gör nedan. De vanligaste minnena idag är annars FLASH-minnen men för vår enkla CPU räcker nedanstående (trodde författaren).

Bilden visar ett basic permanentminne (ROM) realiserat med hjälp av AND och OR-grindar. X representerar den här tre bitar långa adressbussen. W indikerar vilket ord (e.g ordledning) som är programmerat och b indikerar bitarna (e.g bitledningar). På adress 010 (w2) är till exempel ordet 0110 programmerat. Detta blir alltså till data när adressen är 010.

Bilden visar ett permanentminne som man skulle kunna kalla MPROM (Mechanically Programmable Read Only Memory). Här används ju dioder i dom positionerna man vill ha höga och man skulle kunna tänka sig att dessa dioder mekaniskt kan flyttas runt i en "matrissockel". Det är även intressant att notera att då bitledningen i det här fallet är åtta bitar lång så innebär det 256 olika kombinationer. Här används alltså bara fyra. Man skulle dock kunna programmera fyra olika program samtidigt och sedan välja ett åt gången med hjälp av fyra multiplexrar. Alltså fyra olika program samtidigt och valbart i minnet. Dessa skulle alternativt kunna styras att väljas efter varandra och på så sätt utöka programlängden med en faktor fyra.

PLA står för Programmable Logic Array och är ett programmerbart permanentminne eller PROM. Programmeringen är väldigt enkel och utgörs av att diodfunktioner initieras både i AND-delen och i OR-delen. För väldigt små minnen, som i ett instruktionsregister, kan man programmera med hjälp av fysiska dioder enligt figur. Om man på detta sätt "hårdkodar" ett minne bör man dock komma ihåg dels att adressen måste finnas i inverterad form dels att utgången är något högimpediv och bör buffras.

En CPU (Central Processing Unit) är hjärnan i en dator. Instruktionsregistret (IR) är emellertid hjärnan i en CPU. Utan det finns inga möjligheter att tolka och utföra instruktioner. Instruktionerna måste dessutom komma på förutbestämd form annars går hjärnan vilse. Det är lite lustigt att det finns två nivåer av hjärnor här. Kanske man kan kalla själva CPU'n för storhjärnan och IR för lillhjärnan?

Bilden visar en enklast tänkbara maskin vilket skulle kunna representera en mycket enkel CPU där de interna instruktionerna (OP-koder) realiseras. Data ut skulle nämligen kunna användas kombinatoriskt och således styra upp vad som måste göras och i vilken ordning för att till exempel styra ackumulatorn till att realisera en sådan funktion som ROR (Rotate Right) dvs högerskift. Maskinen utnyttjar så kallat pageat minne med vilket menas att varje OP-kod eller instruktion får tilldelat sig en viss minnesarea som räknaren kan stega sig igenom. Detta för att räknaren stegar igenom dom låga bitarna i adressen. Dock är det väl kanske att ta i och kalla detta för en CPU. Ett lämpligare namn vore instruktionsregister (IR).

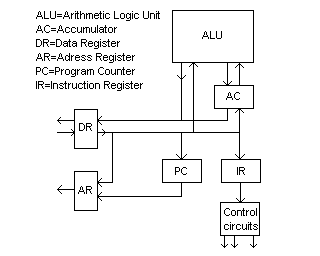
Bilden visar arkitekturen för en någorlunda modern CPU. Den innehåller alltså en enhet för aritmetiska och logiska operationer (ALU), en ackumulator (AC), en programräknare (PC), ett dataregister (DR), ett adressregister (AR), ett instruktionsregister (IR) med diverse kontrollsignaler (Control circuits).

Ovanstående är ett försök att förstå och bygga en CPU. Det har inte alltid förståtts hur man gör varvid författaren har svävat iväg i tämliga flummiga teorier. Med tiden och vartefter har vissa saker dock klarnat varvid boken börjat få lite struktur. Som det känns nu existerar faktiskt få direkta felaktigheter. De felaktigheter som mer eller mindre garanterat finns är de som handlar om den absoluta kodningen av mikroinstruktionerna. Jag tror att ingen människa kan få dom riktigt rätt första gången.

Sen har vi resonemanget runt CPU_1.1 där vi svamlar på om huruvida vi ska spara värdet på stacken eller inte. Detta har vi löst iom våra mikroinstruktioner som innehåller de seglivade PSHA/PULA. Detta är dock inte bra då de kräver typiskt 5 extra klockcykler. Bättre hade varit om vi tagit hjälp av ett temp-register vilket vi också diskuterar i paragrafen.

Det har varit väldigt roligt att försöka sätta på pränt vad man verkligen vet, tror och ibland tycker. Det enda som är lite tråkigt är att det mesta är en massa svammel och jag känner att jag faktiskt varken vill, kan eller orkar göra nåt åt det. Mycket för att det är en del av utvecklingsarbetet och (själv)lärandet.

Kommer det nånsin en ny utgåva så kommer den i så fall på engelska.

• http://www.freescale.com/files/microcontrollers/doc/ref_manual/HCS08RMV1.pdf
• Per-Erik Danielsson, Lennart Bengtsson, Digital Teknik, tredje upplagan, 1986, Sverige
• John P. Hayes, Computer Architecture and Organisation, Second Edition, 1988, Singapore