Gráfico de setores
Gráfico de setores ou gráfico circular, como é tradicionalmente chamado gráfico de pizza é um diagrama circular em que os valores de cada categoria estatística representada são proporcionais às respectivas medidas dos ângulos (1% no gráfico de setor equivale a 3,6º).[1] Enquanto um de seus nomes é associado a sua aparência similar a uma pizza cortada, sua aparência pode variar. O mais antigo uso do gráfico circular é associado à William Playfair "Statistical Breviary" em 1801. São muito utilizados no mundo dos negócios e na mídia, mas eles vêm sendo criticados duramente por profissionais e muitos recomendam não utilizar este tipo de gráfico, apontando o fato que é difícil comparar os setores do gráfico ou comparar a data entre diferentes gráficos circulares. Estes gráficos podem ser facilmente substituídos por outros diagramas como o gráfico de barras.
História
[editar | editar código-fonte]O primeiro uso do gráfico circular é geralmente associado à William Playfair em 1801, onde dois gráficos deste tipo são utilizados. Ele não era utilizado muito no começo; o engenheiro francês Charles Joseph Minard foi um dos primeiros a utilizar em 1858, particularmente em um mapa em que ele precisava adicionar informações em três dimensões. É dito que Florence Nightingale o inventou, mas de fato ela somente popularizou o gráfico e simplesmente foi entendido que ela inventou devido à falta de popularidade da invenção de Playfair.
Exemplo
[editar | editar código-fonte]O exemplo a seguir é baseado no resultado preliminar das Eleições Parlamentares Europeias em 2004. A tabela consiste no numero de assentos alocados para cada partido, além de uma porcentagem do grupo total que eles compõem. Os valores da ultima coluna, que são o ângulo central de cada um dos setores pode ser encontrado multiplicando as porcentagens por 360°

| Grupo | Assentos | Porcentagem (%) | Angulo Central (°) |
|---|---|---|---|
| EUL | 39 | 5.3 | 19.2 |
| PES | 200 | 27.3 | 98.4 |
| EFA | 42 | 5.7 | 20.7 |
| EDD | 15 | 2.0 | 7.4 |
| ELDR | 67 | 9.2 | 33.0 |
| EPP | 276 | 37.7 | 135.7 |
| UEN | 27 | 3.7 | 13.3 |
| Outros | 66 | 9.0 | 32.5 |
| Total | 732 | 99.9* | 360.2* |
*Devido ao arredondamento, o valor total não termina como 100 ou 360.
O tamanho de cada ângulo central é proporcional ao tamanho da quantidade correspondente, neste caso, o numero de assentos. Como a soma dos ângulos centrais deve acabar sempre em 360°, o ângulo que tenha uma fração Q da porcentagem total terá que ter uma proporção de 360Q graus. Neste exemplo, o ângulo central do grupo maior, 'EPP', é 135.7° pois ele é 0.377 vezes o tamanho 360, que arredondado para uma casa decimal depois da vírgula resulta em 135.7°.
Uso, efetividade e percepção visual
[editar | editar código-fonte]
Um problema óbvio na exibição pelo gráfico circular é que eles não podem mostrar mais de alguns valores sem separar a representação visual (os setores) da data que eles representam (tipicamente, porcentagens). Quando os setores se tornam muito pequenos, se deve utilizar cores, texturas ou setas para indicar os setores para que os leitores entendam. Isso faz o gráfico ruim para diagramas com muita informação. Estes gráficos também consumem muito espaço comparados a outros gráficos como o de barra, que raramente precisam de legendas separadas e que podem também apresentar informação como médias ao mesmo tempo.

Estatísticos geralmente consideram gráficos circulares como um método ruim de se apresentar informações, e que eles são raramente utilizados na área científica. Uma razão é que é mais difícil comparar tamanhos de itens de um gráfico quando a área é utilizada ao invés da sua altura e quando diferentes itens são mostrados com formas diferentes.
Além disso, numa pesquisa feita pelos laboratórios "AT&T Bell", foi mostrado que a comparação por ângulos é menos precisa do que por altura. A maioria dos pesquisados tiveram dificuldade em ordenar os gráficos circulares por tamanho, enquanto utilizando o gráfico de barra foram identificados com muito mais facilidade. Similarmente, comparações entre diferente informações era mais fácil com o uso do gráfico de barra. Ainda assim, o gráfico circular pode ser utilizado se está se tentando comparar um setor com o total do gráfico (o circulo todo) e o múltiplo é perto de 25% ou 50%, uma vez que será mais fácil de identificar do que em um gráfico de barra.
Variações e gráficos similares
[editar | editar código-fonte]
Gráfico circular destacado
[editar | editar código-fonte]Este gráfico tem um ou mais setores separados do resto do gráfico. Utilizado principalmente para destacar setores ou para dar visão a setores muito pequenos de um gráfico.
Diagrama de área polar
[editar | editar código-fonte]
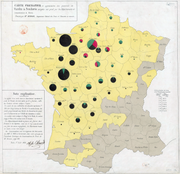
Um Diagrama de Área Polar é similar à um gráfico circular normal, exceto que os setores são de ângulos iguais mas diferem em relação à sua extensão do centro do circulo. O diagrama de área polar é usado para representar fenômenos cíclicos (contagem de mortos por mês, por exemplo). Por exemplo, se a contagem de mortos de cada mês for representada, então haverá 12 setores (um por mês) e todos com o mesmo ângulo de 30 graus. A extensão do centro de cada setor seria proporcional a raiz quadrada dos mortos do mês, então a área do setor representaria o numero de mortos do mês. Se a causa da morte fosse dividida em causa de morte, seria possível fazer varias comparações em um mesmo diagrama, como é demonstrado pelo diagrama ao lado, desenvolvido por Florence Nightingale.
O primeiro uso do diagrama de área polar foi por André-Michel Guerry, o qual ele chamou de curvas circulares em uma apresentação em 1829 mostrando a mudança na direção diária e estacional dos ventos ao ano e o nascimentos e mortes pelas horas do dia. Léon Lalanne mais tarde utilizou o diagrama de área polar para demonstrar a direção dos ventos ao redor de pontos de compasso em 1843. A rosa dos ventos ainda é utilizada por meteorologistas. Nightingale então publicou O Diagrama da Rosa em 1858. O nome "coxcomb" é comumente usado erroneamente: esse era o nome que Nightingale utilizou para se referir ao livro que continha o diagrama ao invés do diagrama.
Gráfico Spie
[editar | editar código-fonte]Uma variação útil do gráfico de área polar é o gráfico spie, criado por Feitelson. Este sobrepõe um gráfico normal circular com uma área polar modificada para permitir comparação de dois conjuntos de informação em dois diferentes estados. A base do gráfico representa o primeiro estado normalmente, com diferente tamanho de setores. O segundo representa é representado por um segundo gráfico sobreposto ao primeiro, usando os mesmos ângulos da base e ajustando a área circular para se encaixar a informação dada. Isso é útil, entre outras coisas, para visualizar desastres entre diferentes grupos populacionais. Por exemplo, a distribuição de primeiro estado pode ser a distribuição de idade e sexo de grupos de uma população, o segundo e mais estados pode representar coisas como mortes por acidentes de carro; idade e sexo de grupos que estão ameaçados de se envolverem em acidentes então ficam muito mais óbvios uma vez que eles vão se estender muito do primeiro estado.
Gráfico multinível
[editar | editar código-fonte]Um gráfico multinível é usado para visualizar informações em hierarquias, mostradas como círculos concêntricos. O circulo no centro representa o nó central, com a hierarquia se expandindo do centro. Um segmento do circulo interno tem uma relação hierárquica com seus segmentos mais exteriores que estão inclusos em sua área angular.
Gráfico circular 3D
[editar | editar código-fonte]O gráfico circular 3D, é utilizado para da à um gráfico um visual tridimensional. Utilizado principalmente por razões estéticas, o gráfico tridimensional não melhora a identificação de uma informação; ao contrario, ele faz a interpretação das informações ainda mais difícil devido ao efeito de perspectiva associado à tridimensionalidade. O uso desnecessário de uma dimensão não utilizada para mostrar informação relevante é desencorajado para gráficos em geral, não somente para gráficos circulares.
Gráfico em Donut
[editar | editar código-fonte]O gráfico em donut é funcionalmente idêntico ao Circular, com a exceção do centro vazio e a habilidade de poder acomodar múltiplas estatísticas ao mesmo tempo. O gráfico em donut é superior ao gráfico circular normal devido a capacidade de mostrar mais informações ao mesmo tempo. Por exemplo, o centro pode ser utilizado para demonstrar mais informações e informações relacionadas como no exemplo.
- ↑ «Gráfico de setores». Encyclopædia Britannica Online (em inglês). Consultado em 22 de novembro de 2019