1 Introduction
A bidirectional transformation (BX) is a pair of mappings between source and view data objects, one in each direction. When the source is updated, a (forward) transformation executes to obtain an updated view. For a variety of reasons, the view may also be subjected to direct manipulation, requiring a corresponding (backward) transformation to keep the source consistent. Much work has gone into this area with applications in databases (Bancilhon & Spyratos, Reference Bancilhon and Spyratos1981; Bohannon et al., Reference Bohannon, Pierce and Vaughan2006; Tran et al., Reference Tran, Kato and Hu2020), software model transformation (Stevens, Reference Stevens2008; He & Hu, Reference He and Hu2018; Tsigkanos et al., Reference Tsigkanos, Li, Jin, Hu and Ghezzi2020; Stevens, Reference Stevens2020), graph transformation (Hidaka et al., Reference Hidaka, Hu, Inaba, Kato, Matsuda and Nakano2010), etc; in particular, there has been several language-based approaches that allow transformations in both directions to be programmed together (e.g., Foster et al., Reference Foster, Greenwald, Moore, Pierce and Schmitt2007;Matsuda et al., Reference Matsuda, Hu, Nakano, Hamana and Takeichi2007; Voigtländer, Reference Voigtländer2009; Ko et al., Reference Ko, Zan and Hu2016).
The lens framework (Foster et al., Reference Foster, Greenwald, Moore, Pierce and Schmitt2007) is the leading approach to BX programming. A lens consists of a pair of transformations: a forward transformation get producing a view from a source, and a backward transformation put which takes a source and a possibly modified view, and reflects the modifications on the view to the source, producing an updated source. It can be represented as a record using Haskell-like notations as:
The additional argument S in put ensures that a view does not have to contain all the information of the source for backward transformation to be viable.
These two transformations should be well behaved in the sense that they satisfy the following round-tripping properties:
The GetPut property requires that no-change to the view should be reflected as no-change to the source, while the PUTGET property requires that all changes in the view should be completely reflected to the source so that the changed view can be successfully recovered by applying the forward transformation to the updated source.
One main advantage of lenses is their modularity. The lens composition
![]() ${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{T}}$
of lenses
${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{T}}$
of lenses
![]() ${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
![]() ${\ell_{\mathrm{2}}\mathbin{:}\textit{V}\leftrightarrow\textit{T}}$
is defined as:Footnote 1
${\ell_{\mathrm{2}}\mathbin{:}\textit{V}\leftrightarrow\textit{T}}$
is defined as:Footnote 1

In the forward direction, lens composition is simply a function composition of the two get functions. In the backward direction, it will first put the updated t’ back to the intermediate v produced by
![]() ${\textit{get}_{\ell_{\mathrm{1}}}\;\textit{s}}$
using
${\textit{get}_{\ell_{\mathrm{1}}}\;\textit{s}}$
using
![]() ${\ell_{\mathrm{2}}}$
, and then put the updated v back to s.
${\ell_{\mathrm{2}}}$
, and then put the updated v back to s.
Lenses are programmed in special languages that preserve round-tripping properties by construction. One popular type of such languages are lens combinators, that is, higher-order functions that construct complex lenses by composing simpler ones. Designing lens languages that are expressive and easy-to-use has been a popular research topic (Bohannon et al., Reference Bohannon, Foster, Pierce, Pilkiewicz and Schmitt2008; Foster et al., Reference Foster, Pilkiewicz and Pierce2008; Barbosa et al., Reference Barbosa, Cretin, Foster, Greenberg and Pierce2010; Hofmann et al., Reference Hofmann, Pierce and Wagner2011; Reference Matsuda and WangMatsuda & Wang, 2015a , 2018; Ko et al., Reference Ko, Zan and Hu2016), effectively creating the paradigm of bidirectional programming.
This flourishing scene of languages invites the next question of software development: what are the suitable methods of BX program construction?
Is there an algebraic theory of lens combinators that would underpin optimization of lens expressions in the same way that the relational algebra and its algebraic theory are used to optimize relational database queries? … This algebraic theory will play a crucial role in a more serious implementation effort. (Foster et al., Reference Foster, Greenwald, Moore, Pierce and Schmitt2007)
Motivated by this question, we propose a calculation framework which optimizes lenses over lists from clear specifications using the algebraic structures of lens combinators.
1.1 Program calculation and the challenge of partiality
Program calculation (Reference BirdBird, 1989b ) is an established technique for reasoning about and optimizing functional programs. The idea is that program developments may benefit from simple properties and laws: equivalences between programming constructs. And consequently, one may calculate with programs — in the same way that one calculates with numeric quantities in algebra — to transform simple specifications into sophisticated and efficient implementations. Each step of a calculation is a step of equational reasoning, where properties of a fragment of the program, such as relations between data structures and algebraic identities, are applied to transform the program structure. A great advantage of this method is that the resulting implementation is guaranteed to be semantically equivalent to the original specification, removing the onerous task of verifying the correctness of the resulting implementation.
Our observation is that program calculation is a good fit to BX programming in a number of different ways. In terms of philosophy, both advocate correctness by construction aiming at significantly reducing the verification and maintenance effort. In terms of representation, both rely heavily on forming programs using composition and computation patterns: in BX languages, the computation patterns are typically captured as lens combinators which are designed to preserve well-behavedness, and in program calculation, the use of computation patterns allows general algebraic laws such as fusion laws and Horner’s rule (Gibbons, Reference Gibbons2002, Reference Gibbons2011) to be applied to specific instances without the need of special analysis.
However, the more complex setting of BX as compared to unidirectional programs posts unique challenges to program calculation. First of all, calculating BX cannot be superficially treated as calculating twice, once in each direction, as the round-tripping properties bind get and put closely together, demanding simultaneous reasoning with both. Moreover, lenses are often partially defined, making it hard to reason about the construction and compositions of combinators like map, fold, and scan. Semantic preservation amid calculation is difficult in this case as well (note that a change in the definedness of a function changes its semantics).
In this context, the term partiality links to round-tripping properties. A lens is partial when its put component cannot successfully restore consistency for certain inputs, even if this function is total (Stevens, Reference Stevens2014). Footnote 2 This partiality can be inherent, where the get component is non-surjective; there is no meaningful put semantics for values outside the codomain of get. This partiality can also be of design choices, as forcing a lens to be total may introduce unwanted complexity. As an example, consider following definition of list mapping as a (high-order) lens which takes a lens
![]() ${\ell}$
of type
${\ell}$
of type
![]() ${\textit{A}\leftrightarrow\textit{B}}$
and return a lens of type
${\textit{A}\leftrightarrow\textit{B}}$
and return a lens of type
![]() ${[\mskip1.5mu \textit{A}\mskip1.5mu]\leftrightarrow[\mskip1.5mu \textit{B}\mskip1.5mu]}$
:
${[\mskip1.5mu \textit{A}\mskip1.5mu]\leftrightarrow[\mskip1.5mu \textit{B}\mskip1.5mu]}$
:
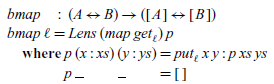
This lens is partial: when the view list is updated to be longer, the put component cannot deal with the inconsistency of the structure (length) between the original source list and the updated view list correctly; it only returns a new source list of the same length as the original one. As a result, the PUTGET property is broken, as shown by
![]() ${\textit{get}_{\textit{bmap}\;\textit{bid}}\;(\textit{put}_{\textit{bmap}\;\textit{bid}}\;[\mskip1.5mu \mathrm{1}\mskip1.5mu]\;[\mskip1.5mu \mathrm{2},\mathrm{3}\mskip1.5mu])\mathrel{=}[\mskip1.5mu \mathrm{2}\mskip1.5mu]\neq[\mskip1.5mu \mathrm{2},\mathrm{3}\mskip1.5mu]}$
where bid is the trivial identity lens. It is common in practice to assume that only certain view updates are permitted, for example, the length of the view list is preserved. With such an assumption, bmap serves as a correct lens.
${\textit{get}_{\textit{bmap}\;\textit{bid}}\;(\textit{put}_{\textit{bmap}\;\textit{bid}}\;[\mskip1.5mu \mathrm{1}\mskip1.5mu]\;[\mskip1.5mu \mathrm{2},\mathrm{3}\mskip1.5mu])\mathrel{=}[\mskip1.5mu \mathrm{2}\mskip1.5mu]\neq[\mskip1.5mu \mathrm{2},\mathrm{3}\mskip1.5mu]}$
where bid is the trivial identity lens. It is common in practice to assume that only certain view updates are permitted, for example, the length of the view list is preserved. With such an assumption, bmap serves as a correct lens.
As a remark, for some lenses such as bmap, it is possible to make their definitions total without contracts and any other constraints on sources and views by using more complicated machinery such as default values (Foster et al., Reference Foster, Greenwald, Moore, Pierce and Schmitt2007; Pacheco & Cunha, Reference Pacheco and Cunha2011). However, giving total definitions to lenses (especially their put components) requires more involved types and semantics and leads to extra programming work for designing lenses. It is totally not necessary to endure this extra complication when we can guarantee that the changes on views always satisfy certain constraints, such as preserving the structures (lengths) of views. Moreover, forcing total definitions also results in challenges to the development of calculation laws, again due to the additional complications of types and semantics. For example, the calculation law of bmap with default values will require additional semantic conditions on them as shown in Appendix A.
In this work, instead of insisting on giving total definitions to all lenses, we use a pair of predicates to constrain the changes on the source and view so that partial lenses can be constructed correctly and composed well. It also facilitates the development of simple but powerful calculation laws.
1.2 Contributions
In this paper, we develop a calculation framework to reason about and optimize bidirectional programs over lists. Our goal is to transform lenses with clear specifications to efficient ones by applying calculation laws. Specifically, we propose an extension to traditional lenses, which we call contract lenses, to enable the construction and composition of possibly partial lenses. We develop several contract-lens combinators, which are high-order functions that characterize key bidirectional computation patterns on lists. And we establish related calculation laws that lay the foundation of a general algebraic theory for BX calculation.
Contract Lenses. The main idea of contract lenses is to utilize a pair of fine-grained predicates, one on source and one on view, to characterize the bidirectional behavior on propagating changes in a compositional way. Composition of contract lenses is justified by the implication relation between the view predicate of the former lens and the source predicate of the latter lens. We also provide an equivalence relation between contract lenses for calculation. (Section 4)
Contract-Lens Combinators. We develop bidirectional computation patterns on the list data structure using contract lenses, including bidirectional fold, map, and scan. An interesting finding is that some bidirectional versions of map and scan cannot be expressed as instances of bidirectional fold due to the requirement of maintaining the consistency of inner dependencies of data structures (Section 5).
Contract-Lens Calculation Laws. We establish calculation laws that transform compositions of such combinators into equivalent but efficient forms. We provide bidirectional versions of many algebraic laws, including fold fusion, map fusion, fold-map fusion, and the scan lemma. These laws comprise a bidirectional algebraic theory that manipulates lenses directly, which underpins the optimization of bidirectional programs (Section 6).
Mechanized Proofs in Agda. We prove the technical details of our calculation framework in Agda, including the correctness of all contract-lens combinators and calculation laws, as well as most of the examples. The proof consists of 4k lines of Agda code (Section 9).
Moreover, we showcase the ability of our framework to construct and calculate lenses by advanced examples that either have intricate partial bidirectional behaviors or are well studied in both BXs and program calculation literature (Section 7). Section 8 discusses related works, and Section 10 concludes.
One thing worth noting is that our primary goal is to propose a calculation framework without restricting to any specific reasoning method. Users are free to calculate contract lenses with pencil/paper proofs following the tradition of program calculation (Reference BirdBird, 1989b ) or formalize the calculation via theorem provers like our mechanized proofs in Agda. It is even possible to develop automatic reasoning tools based on our framework.
2 Background: Program calculation
Program calculation (Reference BirdBird, 1989b ; Gibbons, Reference Gibbons2002) is a technique for constructing efficient programs that are correct by construction. It is suitable for humans to derive efficient programs by hand (Reference BirdBird, 1989b ), as well as for compilers to optimize programs automatically (Gill et al., Reference Gill, Launchbury and Peyton Jones1993; Hu et al., Reference Hu, Iwasaki and Takeichi1996). The principle of program calculation is to express the initial specification of the programming problem in terms of a set of higher-order functions, which support generic algebraic laws, so that an efficient implementation can be calculated through a process of equational reasoning based on the algebraic laws.
2.1 Specification with folds
Fold is a computation pattern that captures structural recursion. In Haskell, there are two versions of fold on list:
![]() ${\textit{foldl}\mathbin{:}(\textit{b}\to \textit{a}\to \textit{b})\to \textit{b}\to [\mskip1.5mu \textit{a}\mskip1.5mu]\to \textit{b}}$
and
${\textit{foldl}\mathbin{:}(\textit{b}\to \textit{a}\to \textit{b})\to \textit{b}\to [\mskip1.5mu \textit{a}\mskip1.5mu]\to \textit{b}}$
and
![]() ${\textit{foldr}\mathbin{:}(\textit{a}\to \textit{b}\to \textit{b})\to \textit{b}\to [\mskip1.5mu \textit{a}\mskip1.5mu]\to \textit{b}}$
, which can be used to define a range of functions. We give some examples as follows, which are also used in the remainder of the paper:
${\textit{foldr}\mathbin{:}(\textit{a}\to \textit{b}\to \textit{b})\to \textit{b}\to [\mskip1.5mu \textit{a}\mskip1.5mu]\to \textit{b}}$
, which can be used to define a range of functions. We give some examples as follows, which are also used in the remainder of the paper:

Here, maximum computes the maximum of a list, sum sums up all the elements in a list, map f applies function f to each element of a list, filter p accepts a list and keeps those elements that satisfy p, scanr keeps the intermediate results of foldr in a list (similarly we have a scanl), inits returns all initial segments (prefix lists) of a list, and tails returns all tail segments (postfix lists) of a list.
Note that foldr f e has two arguments, which can be combined into one foldr’ alg where alg is a function of type
![]() ${\textit{Either}\;()\;(\textit{a},\textit{b})\to \textit{b}}$
:
${\textit{Either}\;()\;(\textit{a},\textit{b})\to \textit{b}}$
:

Now we have
![]() ${\textit{foldr}\;\textit{f}\;\textit{e}\mathrel{=}\textit{foldr'}\;\textit{alg}}$
, where alg is defined below:
${\textit{foldr}\;\textit{f}\;\textit{e}\mathrel{=}\textit{foldr'}\;\textit{alg}}$
, where alg is defined below:
One advantage of writing foldr’ this way is that it can be generalized to arbitrary algebraic data types such as trees (Gibbons, Reference Gibbons2002), and its dual unfoldr’ can be easily defined:

There are some variants of the above functions that will be used later:

The main difference is that they remove the empty list from the result. For example,
![]() ${\textit{inits'}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]\mathrel{=}[\mskip1.5mu [\mskip1.5mu \mathrm{1}\mskip1.5mu],[\mskip1.5mu \mathrm{1},\mathrm{2}\mskip1.5mu],[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]\mskip1.5mu]}$
.
${\textit{inits'}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]\mathrel{=}[\mskip1.5mu [\mskip1.5mu \mathrm{1}\mskip1.5mu],[\mskip1.5mu \mathrm{1},\mathrm{2}\mskip1.5mu],[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]\mskip1.5mu]}$
.
Note that the functions defined with fold are all executable programs. But we call them specifications in the context of program calculation because such definitions (despite being clear and concise) are not necessarily efficient (especially when multiple folds are composed together). Program calculation is about turning such specifications into more efficient (though likely less clear) implementations.
2.2 Algebraic laws
The foundation of program calculation is the algebraic laws, which can be applied step by step to derive efficient implementations. The most important algebraic law for fold is the foldr fusion law:
It states that a function h composed with a foldr’ can be fused into a single foldr’ if the fusible condition
![]() ${\textit{h}\,{\circ }\textit{f}\mathrel{=}\textit{g}\,{\circ }\mathrm{F_L}\;\textit{h}}$
is satisfied. Note that
${\textit{h}\,{\circ }\textit{f}\mathrel{=}\textit{g}\,{\circ }\mathrm{F_L}\;\textit{h}}$
is satisfied. Note that
![]() ${\mathrm{F_L}}$
is the so-called list functor, which is defined by:
${\mathrm{F_L}}$
is the so-called list functor, which is defined by:
where
![]() ${\mathbin{+}} and {\mathbin{\times}}$
on functions are defined by
${\mathbin{+}} and {\mathbin{\times}}$
on functions are defined by
![]() ${(\textit{f}\mathbin{+}\textit{g})\;(\textit{Left}\;\textit{x})\mathrel{=}\textit{Left}\;(\textit{f}\;\textit{x})}$
,
${(\textit{f}\mathbin{+}\textit{g})\;(\textit{Left}\;\textit{x})\mathrel{=}\textit{Left}\;(\textit{f}\;\textit{x})}$
,
![]() ${(\textit{f}\mathbin{+}\textit{g})\;(\textit{Right}\;\textit{y})\mathrel{=}\textit{Right}\;(\textit{g}\;\textit{y})}$
, and
${(\textit{f}\mathbin{+}\textit{g})\;(\textit{Right}\;\textit{y})\mathrel{=}\textit{Right}\;(\textit{g}\;\textit{y})}$
, and
![]() ${(\textit{f}\mathbin{\times}\textit{g})\;(\textit{x},\textit{y})\mathrel{=}(\textit{f}\;\textit{x},\textit{g}\;\textit{y})}$
. The function
${(\textit{f}\mathbin{\times}\textit{g})\;(\textit{x},\textit{y})\mathrel{=}(\textit{f}\;\textit{x},\textit{g}\;\textit{y})}$
. The function
![]() ${\textit{const}} and {\textit{id}}$
are defined by
${\textit{const}} and {\textit{id}}$
are defined by
![]() ${\textit{const}\;\textit{x}\;\_ \mathrel{=}\textit{x}}$
and
${\textit{const}\;\textit{x}\;\_ \mathrel{=}\textit{x}}$
and
![]() ${\textit{id}\;\textit{x}\mathrel{=}\textit{x}}$
.
${\textit{id}\;\textit{x}\mathrel{=}\textit{x}}$
.
There is a corresponding fusion law for foldl too. And for some special cases of fold, the fusible conditions are always satisfied and therefore omitted from the laws:
Note that
![]() ${\mathrm{F_m}}$
is the so-called map functor, which is defined by:
${\mathrm{F_m}}$
is the so-called map functor, which is defined by:
It is worth noting that it is possible for an algebraic law to abstract a complex derivation step. For instance, the following Horner’s lemma shows a big step to fuse a complex composition into a single foldl.
Lemma 1 (Horner’s Rule). Let
![]() ${\oplus}$
and
${\oplus}$
and
![]() ${\otimes}$
are associative operators. Suppose
${\otimes}$
are associative operators. Suppose
![]() ${\otimes}$
distributes through
${\otimes}$
distributes through
![]() ${\oplus}$
and b is a left-identity of
${\oplus}$
and b is a left-identity of
![]() ${\oplus}$
, then:
${\oplus}$
, then:
where
![]() $x\odot y=(x\otimes y)\oplus a$
, and a is the value passed to
$x\odot y=(x\otimes y)\oplus a$
, and a is the value passed to
![]() ${\textit{foldl}\;(\otimes)}$
.
${\textit{foldl}\;(\otimes)}$
.
2.3 A calculational example
The maximum segment sum problem (mss for short) is to compute the maximum of the sums of the segments in a list. Developing an efficient implementation of it is challenging, and it has become a classic example to show off the power of program calculation.
The idea is to start with a straightforward specification as follows:
Given a list, we first enumerate all the segments by
![]() ${\textit{map}\;\textit{tails}\,{\circ }\textit{inits}}$
. Then we calculate the sum of all segments by
${\textit{map}\;\textit{tails}\,{\circ }\textit{inits}}$
. Then we calculate the sum of all segments by
![]() ${\textit{map}\;(\textit{map}\;\textit{sum})}$
and get the maximum of these results of sum by
${\textit{map}\;(\textit{map}\;\textit{sum})}$
and get the maximum of these results of sum by
![]() ${\textit{maximum}\,{\circ }\textit{map}\;\textit{maximum}}$
. This implementation is easy to understand but very inefficient (
${\textit{maximum}\,{\circ }\textit{map}\;\textit{maximum}}$
. This implementation is easy to understand but very inefficient (
![]() $O(n^3)$
where n is the length of the list). Through program calculation, one can step-by-step rewrite the program through applying a sequence of algebraic laws to reach a version that has time complexity O(n). The details of the calculation can be found in Reference BirdBird (1989a
).
$O(n^3)$
where n is the length of the list). Through program calculation, one can step-by-step rewrite the program through applying a sequence of algebraic laws to reach a version that has time complexity O(n). The details of the calculation can be found in Reference BirdBird (1989a
).
The challenge that this paper aims to address is: Can the same be done for bidirectional programs — deriving efficient lenses from clear specifications?
3 Overview
In this section, we informally introduce contract lenses and demonstrate how they facilitate the construction of a bidirectional program calculation framework.
3.1 Taming partiality with contract lenses
The core idea of contract lenses is to enrich traditional lenses with source and view conditions (also called contracts) restricting the changes on source and view, as below:
where ℓ is a lens with only get and put. The contracts are highlighted through the paper. Though we write cs and cv around the lens ℓ for readability in this section, a contract lens is formally defined as a four-tuple consisting of get, put, cs, and cv.Footnote 3
This is a BX setting, so we assume that it is the views that are actively updated and the sources are passively changed accordingly. Given a source s and an updated view v, the view condition cv is a predicate that takes two arguments: the original view
![]() ${\textit{get}_{\ell}\;\textit{s}}$
and updated view v, restricting the permitted values of the updated view in relation to the original view. The source condition cs has a similar structure. It takes two arguments: the original source s and the updated source
${\textit{get}_{\ell}\;\textit{s}}$
and updated view v, restricting the permitted values of the updated view in relation to the original view. The source condition cs has a similar structure. It takes two arguments: the original source s and the updated source
![]() ${\textit{put}_{\ell}\;\textit{s}\;\textit{v}}$
, specifying an invariant that must hold for source changes as a result of valid view changes.
${\textit{put}_{\ell}\;\textit{s}\;\textit{v}}$
, specifying an invariant that must hold for source changes as a result of valid view changes.
For the list mapping lens bmap we have seen in the introduction, we are interested in a condition that rules out any changes to the structure (length) of the view, which we specify as the following predicate:
This condition is enough to ensure that the put component of bmap can always restore consistency between the updated view and source without breaking the round-tripping properties. In addition, we can conclude for bmap that if the view length does not change, the source length does not change either. This gives rise to the following contract lens where
![]() ${{\{\textit{eqlength}\}}}$
serves as both the view and source conditions:Footnote 4
${{\{\textit{eqlength}\}}}$
serves as both the view and source conditions:Footnote 4
Two lenses can be composed if the view condition of the former matches the source condition of the latter. For example, we can compose two bmaps:
With contract lenses, the partiality issues of lens composition is reduced to local reasoning of adjacent conditions. Moreover, since we always want the modification on view (and source) to satisfy the contracts, the round-tripping properties also only need to hold when the contracts are satisfied, which significantly simplify the design of lenses. For instance, when designing
![]() ${{\{\textit{eqlength}\}}\;\textit{bmap}\;\ell\;{\{\textit{eqlength}\}}}$
, we do not need to consider how to put back the changes to source when the length of view is changed any more.
${{\{\textit{eqlength}\}}\;\textit{bmap}\;\ell\;{\{\textit{eqlength}\}}}$
, we do not need to consider how to put back the changes to source when the length of view is changed any more.
The idea of introducing contracts is natural because when updating a view of type V in a BX setting, we usually want the updated view to satisfy certain constraints (like being of the same length as the original view), instead of allowing it to be any value of type V. Another option of solving the partiality problem is to give total definitions to all lenses. However, as we have discussed in Section 1.1, it leads to several obstacles to designing lenses and developing a calculation framework, which we avoid by using contracts lenses.
3.2 Calculation with contract lenses
Once we have established the composition of contract lenses, we can start to design a calculation framework for lenses.
For the sake of demonstration, we start with a contrived example: given a list of nonempty lists, we extract all head elements of the lists and then filter out the even elements. (More realistic examples will be given in Section 7.) In the unidirectional setting, one can apply the Fold-Map Fusion law to fuse the two passes of the list as follows: Footnote 5

With contract-lens combinators, we can give a bidirectional version of the specification:
The view condition of
![]() ${\textit{bfilter}\;\textit{even}}$
is defined as:
${\textit{bfilter}\;\textit{even}}$
is defined as:
which depends on the predicate even.Footnote 6 The combinator bfilter is a bidirectional version of filter implemented by bfoldr’, which is a bidirectional version of foldr with contracts (Section 5). We have already seen bmap in Section 1.1. In this example, bfilter even is also given source and view conditions including eqlength, which is needed to be composed with
![]() ${{\{\textit{eqlength}\}}\;\textit{bmap}\;\textit{bhead}\;{\{\textit{eqlength}\}}}$
. The contracts of
${{\{\textit{eqlength}\}}\;\textit{bmap}\;\textit{bhead}\;{\{\textit{eqlength}\}}}$
. The contracts of
![]() ${{\{\textit{eqlength}\}}\;\textit{bfilter}\;\textit{even}\;{\{\textit{ceven}\}}}$
make sense: if the number of even elements is not changed, the total number of elements will neither be changed because the odd elements, which do not appear in the view, remain invariant.
${{\{\textit{eqlength}\}}\;\textit{bfilter}\;\textit{even}\;{\{\textit{ceven}\}}}$
make sense: if the number of even elements is not changed, the total number of elements will neither be changed because the odd elements, which do not appear in the view, remain invariant.
The advantage of calculating with contract lenses is that we only need to care about the round-tripping properties under the source and view conditions, which simplifies the design of lenses, and as a result simplifies the calculation laws. For bfoldr’, we have a bidirectional version of Fold-Map Fusion law called BFoldr’-BMap Fusion, with which we can bidirectionalize the calculation process of
![]() ${\textit{filter}\;\textit{even}\,{\circ }\textit{map}\;\textit{head}}$
we have seen before:Footnote 7
${\textit{filter}\;\textit{even}\,{\circ }\textit{map}\;\textit{head}}$
we have seen before:Footnote 7

The bmapF is a bidirectional version of
![]() ${\mathrm{F_m}}$
used in the Fold-Map Fusion law, and the bfilterAlg even is a bidirectional version of
${\mathrm{F_m}}$
used in the Fold-Map Fusion law, and the bfilterAlg even is a bidirectional version of
![]() ${\lambda \textit{a}\;\textit{r}\to \mathbf{if}\;\textit{even}\;\textit{a}\;\mathbf{then}\;\textit{a}\mathbin{:}\textit{r}\;\mathbf{else}\;\textit{r}}$
defined in Section 5.1.2.
${\lambda \textit{a}\;\textit{r}\to \mathbf{if}\;\textit{even}\;\textit{a}\;\mathbf{then}\;\textit{a}\mathbin{:}\textit{r}\;\mathbf{else}\;\textit{r}}$
defined in Section 5.1.2.
This “banality” of the calculation is the strength of our framework, as we have successfully set up a system that allows programmers to reason about lenses in almost exactly the same way as they have done for unidirectional programs for decades. In the rest of the paper, we will formally develop the contract lens framework and continue to demonstrate the kind of reasoning that it enables through examples far more advanced than the ones we have seen in this section.
4 Contract lenses
In this section, we formally define contract lenses, a natural extension of the traditional lenses with contracts. This novel construction enables us to express a wide class of partial BXs while ensuring safe and modular composition.
4.1 Contract lenses
Lenses essentially manipulate changes. A put propagates a change in view back to a change in source with respect to a get function. As we have already seen in Section 3, to guarantee correct change propagation, we extend lenses with a pair of constraints, cs and cv, describing the conditions of changes in the source and the view, respectively.
Definition 1 (Contract Lenses).
A contract lensFootnote 8 between source of type S and view of type V consists of a pair of transformations get and put together with a pair of relations: a source condition
![]() ${\textit{cs}\mathbin{:}\textit{S}\to \textit{S}\to \textit{Set}}$
and a view condition
${\textit{cs}\mathbin{:}\textit{S}\to \textit{S}\to \textit{Set}}$
and a view condition
![]() ${\textit{cv}\mathbin{:}\textit{V}\to \textit{V}\to \textit{Set}}$
.
${\textit{cv}\mathbin{:}\textit{V}\to \textit{V}\to \textit{Set}}$
.
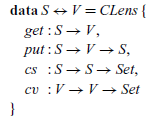
where the following round-tripping properties are satisfied for every
![]() ${\textit{s}\mathbin{:}\textit{S}}$
and
${\textit{s}\mathbin{:}\textit{S}}$
and
![]() ${\textit{v}\mathbin{:}\textit{V}}$
:
${\textit{v}\mathbin{:}\textit{V}}$
:
For backward transformations, the BackwardValidity law and the ConditionedPutget say that if the change in the view satisfies cv, then the change in the source should satisfy cs, and the put-get law holds. For forward transformations, the ForwardValidity law and the ConditionedGetPut say that if the source s satisfies cs s s, then the view get s should satisfy cv, and the get-put law holds. The condition
![]() ${\textit{cs}\;\textit{s}\;\textit{s}}$
in the ConditionedGetPut law is necessary to keep the system consistent: if the get-put law
${\textit{cs}\;\textit{s}\;\textit{s}}$
in the ConditionedGetPut law is necessary to keep the system consistent: if the get-put law
![]() ${\textit{put}\;\textit{s}\;(\textit{get}\;\textit{s})\mathrel{=}\textit{s}}$
holds, replacing v with get s in the BackwardValidity law, we have cs s (put s (get s))=cs s s. The BackwardValidity law and ForwardValidity law are important for the proof of the Theorem 1, which states that the composition of contract lenses preserves round-tripping properties. Essentially, they guarantee that the contracts are propagated by get and put.
${\textit{put}\;\textit{s}\;(\textit{get}\;\textit{s})\mathrel{=}\textit{s}}$
holds, replacing v with get s in the BackwardValidity law, we have cs s (put s (get s))=cs s s. The BackwardValidity law and ForwardValidity law are important for the proof of the Theorem 1, which states that the composition of contract lenses preserves round-tripping properties. Essentially, they guarantee that the contracts are propagated by get and put.
We have a few remarks to make here.
First, as we have discussed in Section 1, all functions including get and put components of lenses are total in this paper. For simplicity, some function definitions are abridged and lack some catch-all patterns. Complete definitions of these functions can be found in the Agda formalization.
Second, to be more consistent with our Agda formalisation, we use the Set type in Agda to represent the type for predicates. Note that any value b of type Bool can be transformed into Set by using the expression b=True. For readability, we allow this transformation to be implicit in the rest of the paper. That is to say, anywhere a value of type Set is needed, we can fill in a value of type Bool.
Third, the role of source conditions in contract lenses are primarily for describing the “effect” on source updates after ruling out those view updates, which can be seen in the rule BackwardValidity: when inputs are restricted to satisfy the view condition, the corresponding outputs are guaranteed to satisfy the source condition. This guarantee is necessary for contract-lens composition. The rule ForwardValidity and ConditionedGetPut are conditioned on cs s s, a predicate on the identity source update, which should hold in most of the cases. The requirement here is necessary for proving the correctness of contract-lens composition. Also note that even though we add conditions to the traditional GETPUT and PUTGET laws, we do not weaken the properties of lenses. Since we always want them to hold, the condition cv (get s) v should always be satisfied when we compute put s v, and the condition cs s s should always be satisfied when we compute get s. Footnote 9
We use the following notational conventions:
-
• We use
 ${\textit{cs}_{\ell},\textit{cv}_{\ell},\textit{get}_{\ell},\textit{put}_{\ell}}$
to refer to the source condition, view condition, forward transformation, and backward transformation of a contract lens
${\textit{cs}_{\ell},\textit{cv}_{\ell},\textit{get}_{\ell},\textit{put}_{\ell}}$
to refer to the source condition, view condition, forward transformation, and backward transformation of a contract lens
 ${\ell}$
, respectively.
${\ell}$
, respectively. -
• Lists start from index 1 and the notation
 ${\textit{x}_{\textit{i}}}$
refers to the i-th element of a list x.
${\textit{x}_{\textit{i}}}$
refers to the i-th element of a list x.
Now we give some simple examples of contract lenses. We leave more interesting examples in Section 5.
Example 1 (Embedding Traditional Lenses into Contract Lenses). As contract lenses are extensions of traditional lenses, traditional lenses can be embedded into contract lenses by adding dummy conditions ctrue, where
![]() ${\textit{ctrue}\;\_ \_ \mathrel{=} \top }$
.
${\textit{ctrue}\;\_ \_ \mathrel{=} \top }$
.
Example 2 (Bidirectional Inits). An interesting example is a bidirectional version of inits’ defined in Section 2.1. The view condition essentially describes the range of the inits’. It is a little complicated, but this kind of detailed specification is needed for calculation:
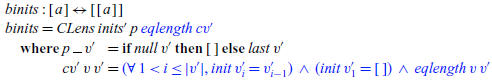
With the help of the condition on the view change (which keeps the “inits” structure), our putback function becomes very simple, just returning the last element if it is not empty.
4.2 Composition of contract lenses
Contract lenses are compositional, which is similar to that of traditional lenses, except that we need to be sure that the change conditions match well.
Definition 2 (Composition of Contract Lenses). For two contract lenses
![]() ${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
![]() ${\ell_{\mathrm{2}}\mathbin{:}\textit{V}\leftrightarrow\textit{T}}$
, if
${\ell_{\mathrm{2}}\mathbin{:}\textit{V}\leftrightarrow\textit{T}}$
, if
![]() ${\forall\;(\textit{v}\mathbin{:}\textit{V})\;(\textit{v'}\mathbin{:}\textit{V}),\textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v'}\Rightarrow \textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v'}}$
and
${\forall\;(\textit{v}\mathbin{:}\textit{V})\;(\textit{v'}\mathbin{:}\textit{V}),\textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v'}\Rightarrow \textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v'}}$
and
![]() ${\forall\;\textit{v}\mathbin{:}\textit{V},\textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v}\Rightarrow \textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v}}$
hold, then they can be composed into a contract lens
${\forall\;\textit{v}\mathbin{:}\textit{V},\textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v}\Rightarrow \textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v}}$
hold, then they can be composed into a contract lens
![]() ${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{T}}$
as defined below.
${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{T}}$
as defined below.

Theorem 1 (Well-behaved Composition). For any two contract lenses
![]() ${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
![]() ${\ell_{\mathrm{2}}\mathbin{:}\textit{V}\leftrightarrow\textit{T}}$
, their composition
${\ell_{\mathrm{2}}\mathbin{:}\textit{V}\leftrightarrow\textit{T}}$
, their composition
![]() ${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{T}}$
satisfies the round-tripping properties.
${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{T}}$
satisfies the round-tripping properties.
Notice that we not only require the backward implication
![]() ${\textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v'}\Rightarrow \textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v'}}$
, but also the forward one
${\textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v'}\Rightarrow \textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v'}}$
, but also the forward one
![]() ${\textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v}\Rightarrow \textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v}}$
. Intuitively, the latter is used to establish a connection between the ForwardValidity law of
${\textit{cv}_{\ell_{\mathrm{1}}}\;\textit{v}\;\textit{v}\Rightarrow \textit{cs}_{\ell_{\mathrm{2}}}\;\textit{v}\;\textit{v}}$
. Intuitively, the latter is used to establish a connection between the ForwardValidity law of
![]() ${\ell_{1}}$
and
${\ell_{1}}$
and
![]() ${\ell_{2}}$
. Moreover, we can strengthen the condition of composition to make it easier to use. We say that two predicates
${\ell_{2}}$
. Moreover, we can strengthen the condition of composition to make it easier to use. We say that two predicates
![]() ${\textit{c}_{\mathrm{1}}\mathbin{:}\textit{A}\to \textit{A}\to \textit{Set}}$
and
${\textit{c}_{\mathrm{1}}\mathbin{:}\textit{A}\to \textit{A}\to \textit{Set}}$
and
![]() ${\textit{c}_{\mathrm{2}}\mathbin{:}\textit{B}\to \textit{B}\to \textit{Set}}$
are equivalent, written as
${\textit{c}_{\mathrm{2}}\mathbin{:}\textit{B}\to \textit{B}\to \textit{Set}}$
are equivalent, written as
![]() ${\textit{c}_{\mathrm{1}}\Leftrightarrow\textit{c}_{\mathrm{2}}}$
, if
${\textit{c}_{\mathrm{1}}\Leftrightarrow\textit{c}_{\mathrm{2}}}$
, if
![]() ${\textit{A}\mathrel{=}\textit{B}}$
and
${\textit{A}\mathrel{=}\textit{B}}$
and
![]() ${\forall\;(\textit{a}\mathbin{:}\textit{A})\;(\textit{a'}\mathbin{:}\textit{A}),\textit{c}_{\mathrm{1}}\;\textit{a}\;\textit{a'}\Leftrightarrow\textit{c}_{\mathrm{2}}\;\textit{a}\;\textit{a'}}$
. The condition of composition can be strengthened to
${\forall\;(\textit{a}\mathbin{:}\textit{A})\;(\textit{a'}\mathbin{:}\textit{A}),\textit{c}_{\mathrm{1}}\;\textit{a}\;\textit{a'}\Leftrightarrow\textit{c}_{\mathrm{2}}\;\textit{a}\;\textit{a'}}$
. The condition of composition can be strengthened to
![]() ${\textit{cs}_{\ell_{\mathrm{2}}}\Leftrightarrow\textit{cv}_{\ell_{\mathrm{1}}}}$
, which is sufficient in most cases.
${\textit{cs}_{\ell_{\mathrm{2}}}\Leftrightarrow\textit{cv}_{\ell_{\mathrm{1}}}}$
, which is sufficient in most cases.
4.3 Equivalence of contract lenses
Now we define an equivalence relation over contract lenses.
Definition 3 (Lens Equivalence). For lens
![]() ${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
${\ell_{\mathrm{1}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
and
![]() ${\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
, we say
${\ell_{\mathrm{2}}\mathbin{:}\textit{S}\leftrightarrow\textit{V}}$
, we say
![]() ${\ell_{\mathrm{1}}}$
is equivalent to
${\ell_{\mathrm{1}}}$
is equivalent to
![]() ${\ell_{\mathrm{2}}}$
, written as
${\ell_{\mathrm{2}}}$
, written as
![]() ${\ell_{\mathrm{1}}=\ell_{\mathrm{2}}}$
, if
${\ell_{\mathrm{1}}=\ell_{\mathrm{2}}}$
, if
-
•
 ${\textit{cs}_{\ell_{\mathrm{1}}}\Leftrightarrow\textit{cs}_{\ell_{\mathrm{2}}}}$
${\textit{cs}_{\ell_{\mathrm{1}}}\Leftrightarrow\textit{cs}_{\ell_{\mathrm{2}}}}$
-
•
 ${\textit{cv}_{\ell_{\mathrm{1}}}\Leftrightarrow\textit{cv}_{\ell_{\mathrm{2}}}}$
${\textit{cv}_{\ell_{\mathrm{1}}}\Leftrightarrow\textit{cv}_{\ell_{\mathrm{2}}}}$
-
•
 ${\forall\;\textit{s}\mathbin{:}\textit{S},\textit{get}_{\ell_{\mathrm{1}}}\;\textit{s}=\textit{get}_{\ell_{\mathrm{2}}}\;\textit{s}}$
${\forall\;\textit{s}\mathbin{:}\textit{S},\textit{get}_{\ell_{\mathrm{1}}}\;\textit{s}=\textit{get}_{\ell_{\mathrm{2}}}\;\textit{s}}$
-
•
 ${\forall\;(\textit{s}\mathbin{:}\textit{S})\;(\textit{v}\mathbin{:}\textit{V}),\textit{cv}_{\ell_{\mathrm{1}}}\;(\textit{get}_{\ell_{\mathrm{1}}}\;\textit{s})\;\textit{v}\Rightarrow \textit{put}_{\ell_{\mathrm{1}}}\;\textit{s}\;\textit{v}=\textit{put}_{\ell_{\mathrm{2}}}\;\textit{s}\;\textit{v}}$
${\forall\;(\textit{s}\mathbin{:}\textit{S})\;(\textit{v}\mathbin{:}\textit{V}),\textit{cv}_{\ell_{\mathrm{1}}}\;(\textit{get}_{\ell_{\mathrm{1}}}\;\textit{s})\;\textit{v}\Rightarrow \textit{put}_{\ell_{\mathrm{1}}}\;\textit{s}\;\textit{v}=\textit{put}_{\ell_{\mathrm{2}}}\;\textit{s}\;\textit{v}}$
Theorem 2 (Lens Equivalence is an Equivalence Relation). The equivalence relation between contract lenses is reflexive, symmetric, and transitive.
There is nothing special about this definition of the equivalence relation. The equivalence relation for contract lenses is the base for our equational program reasoning and plays an important role in developing our program calculation theory of contract lenses.
5 Contract-lens combinators
Lens combinators have become a popular approach to programming BXs because of their modularity and correctness-by-construction. In this section, we define several lens combinators to capture fundamental patterns (higher-order functions) for easy construction of complex contract lenses in a compositional manner as well as to demonstrate the expressiveness and flexibility of our new contract lens framework.
Since BXs can be considered as unidirectional forward programs with additional put semantics, our idea is to bidirectionalize widely used recursion schemes in (forward) functional programming including fold, map, filter, and scan. The main challenge is that these functions are usually not bijective, which requires contracts to make them total and suitable for calculation. Different contracts will lead to different bidirectional version of the same high-order functions and are useful for different situations. We will give both total bidirectional versions of these functions, and their variants which have some additional conditions on the source and the view to make them flexible for composing with each other. It will be interesting to see later that although map and scan can be implemented by fold, it turns out to be more useful to implement bidirectional versions of map and scan individually to attain better control over their contracts and behaviors.
5.1 Bidirectional fold
As we have seen in Section 2.1, folds are of vital importance in program calculation. We start with bfoldr, a bidirectional version of foldr’, with trivial source and view conditions:
One challenge for designing higher-order contract lenses is that they usually impose certain constraints to the contracts of their lens parameters. For instance, a trivial bidirectional version of foldr’ requires the parameter lens to have the trivial contract ctrue. To specify such requirements, we use similar syntax to refinement types, which is easily readable and understandable by humans and is also suitable for pencil/paper proofs. In theorem provers, one could use existential types to express the requirements of contracts like our Agda formalization.
We introduce the following syntactic sugar to specify the source and view conditions of parameters for higher-order contract lenses:
The type of bfoldr can be simplified to
Given a simple contract lens
![]() ${\ell\mathbin{:}\textit{Either}\;()\;(\textit{S},\textit{V})\leftrightarrow\textit{V}}$
with trivial contracts,
${\ell\mathbin{:}\textit{Either}\;()\;(\textit{S},\textit{V})\leftrightarrow\textit{V}}$
with trivial contracts,
![]() ${\textit{bfoldr}\;\ell}$
returns a contract lens of type
${\textit{bfoldr}\;\ell}$
returns a contract lens of type
![]() ${[\mskip1.5mu \textit{S}\mskip1.5mu]\leftrightarrow\textit{V}}$
also with trivial contracts, synchronizing a list of type
${[\mskip1.5mu \textit{S}\mskip1.5mu]\leftrightarrow\textit{V}}$
also with trivial contracts, synchronizing a list of type
![]() ${[\mskip1.5mu \textit{S}\mskip1.5mu]}$
with a value of type V. For the get direction, we simply use the unidirectional foldr’. For the put direction, we recursively construct an updated source list (using unfoldr’) from the original source and an updated view step by step through
${[\mskip1.5mu \textit{S}\mskip1.5mu]}$
with a value of type V. For the get direction, we simply use the unidirectional foldr’. For the put direction, we recursively construct an updated source list (using unfoldr’) from the original source and an updated view step by step through
![]() ${\textit{put}_{\ell}}$
, the backward transformation of
${\textit{put}_{\ell}}$
, the backward transformation of
![]() ${\ell}$
. Formally, we define bfoldr as follows:
${\ell}$
. Formally, we define bfoldr as follows:

Note that the put direction of the above definition is inefficient since it computes “g as” every time
![]() ${\textit{coalg}\;(\textit{a}\mathbin{:}\textit{as},\textit{v'})}$
is called. A more efficient implementation is to calculate all g as in advance using a scanr as shown in Appendix B.1. We will use the efficient definition of bfoldr in the following sections.
${\textit{coalg}\;(\textit{a}\mathbin{:}\textit{as},\textit{v'})}$
is called. A more efficient implementation is to calculate all g as in advance using a scanr as shown in Appendix B.1. We will use the efficient definition of bfoldr in the following sections.
Similarly, we can define bfoldl, which is omitted here. The following example shows how the bidirectional fold works.
Example 3 (Bidirectional Maximum). Considering that we want to synchronize a list with its maximum, we can define it in terms of bfoldr by
where bmax is a bidirectional version of max whose backward transformation uses the modified value to replace the maximum value of the parameter pair:Footnote 10

To see a computation instance of bmaximum, we refer to Appendix C.1.
5.1.1 Bidirectional fold: Preserving length and transmitting constraints
While bfoldr is useful when it is total in both get and put directions, we may wish to keep the length of the source unchanged after put. For example, considering the bmaximum in Example 3, we may wish to keep the length of the source list after
![]() ${\textit{put}_{\textit{bmaximum}}}$
, and furthermore, we hope that the source and view conditions of bfoldr be able to express some extra constraints on the elements. All these can be concisely expressed as the following higher-order contract lens:
${\textit{put}_{\textit{bmaximum}}}$
, and furthermore, we hope that the source and view conditions of bfoldr be able to express some extra constraints on the elements. All these can be concisely expressed as the following higher-order contract lens:

The lift and licond, two high-order predicates, require their arguments to be of the same shape and structurally lift predicates over sum types (Either) and list types, respectively:

The lens combinator bfoldr’ takes two predicates
![]() ${\widehat {\textit{cs}}}$
and
${\widehat {\textit{cs}}}$
and
![]() ${\widehat {\textit{cv}}}$
and have the same definition of get and put components as bfoldr. The
${\widehat {\textit{cv}}}$
and have the same definition of get and put components as bfoldr. The
![]() ${\widehat {\textit{cs}}}$
represents the constraints on the elements of the source list, and the
${\widehat {\textit{cs}}}$
represents the constraints on the elements of the source list, and the
![]() ${\widehat {\textit{cv}}}$
represents the view condition. Notice that the predicate parameters
${\widehat {\textit{cv}}}$
represents the view condition. Notice that the predicate parameters
![]() ${\widehat {\textit{cs}}}$
and
${\widehat {\textit{cs}}}$
and
![]() ${\widehat {\textit{cv}}}$
are kind of administrative; their main role is to guarantee that the source condition of the parameter lens is of shape
${\widehat {\textit{cv}}}$
are kind of administrative; their main role is to guarantee that the source condition of the parameter lens is of shape
![]() ${\textit{lift}\;\textit{cs}'\;\textit{cv}'}$
for some cs’ and cv’. Idealy, we can make them existentially bound. We opt to have explicit predicate parameters to make the presentation clear and more consistent with our Agda formalization.
${\textit{lift}\;\textit{cs}'\;\textit{cv}'}$
for some cs’ and cv’. Idealy, we can make them existentially bound. We opt to have explicit predicate parameters to make the presentation clear and more consistent with our Agda formalization.
Example 4 (Bidirectional Maximum Preserving Length). A direct use of bfoldr’ is to define a bidirectional version of maximum that preserves the length of the source list.

One may doubt that the
![]() ${\textit{put}\;(\textit{Left}\;())\;\textit{v'}\mathrel{=}\textit{Right}\;(\textit{v'},\mathbin{-}\infty)}$
in bmax’ might break the equal length condition. In fact, it will never be executed because the view condition requires the maximum value to be unchanged when it is
${\textit{put}\;(\textit{Left}\;())\;\textit{v'}\mathrel{=}\textit{Right}\;(\textit{v'},\mathbin{-}\infty)}$
in bmax’ might break the equal length condition. In fact, it will never be executed because the view condition requires the maximum value to be unchanged when it is
![]() ${\mathbin{-}\infty}$
.
${\mathbin{-}\infty}$
.
5.1.2 Bidirectional filter
As an application of bidirectional folds, we construct the bidirectional filter, which appears frequently in application scenarios of BXs, often in the forms of explicit combinators (Foster et al., Reference Foster, Greenwald, Moore, Pierce and Schmitt2007) or SQL selection commands (Abou-Saleh et al., Reference Abou-Saleh, Cheney, Gibbons, McKinna and Stevens2018).
The unidirectional version of
![]() ${\textit{filter}}$
can be implemented by foldr as
${\textit{filter}}$
can be implemented by foldr as
![]() ${\textit{filter}\;\textit{pr}\mathrel{=}\textit{foldr}\;(\lambda \textit{x}\;\textit{xs}\to \mathbf{if}\;\textit{pr}\;\textit{x}\;\mathbf{then}\;\textit{x}\mathbin{:}\textit{xs}\;\mathbf{else}\;\textit{xs})\;[\mskip1.5mu \mskip1.5mu]}$
, which returns a list of elements satisfying the predicate pr. With the bfoldr’ introduced above, we are able to define a bidirectional version of filter which preserves the lengths of the source and view lists:
${\textit{filter}\;\textit{pr}\mathrel{=}\textit{foldr}\;(\lambda \textit{x}\;\textit{xs}\to \mathbf{if}\;\textit{pr}\;\textit{x}\;\mathbf{then}\;\textit{x}\mathbin{:}\textit{xs}\;\mathbf{else}\;\textit{xs})\;[\mskip1.5mu \mskip1.5mu]}$
, which returns a list of elements satisfying the predicate pr. With the bfoldr’ introduced above, we are able to define a bidirectional version of filter which preserves the lengths of the source and view lists:

The function fcond is defined as
![]() ${\textit{fcond}\;\textit{pr}\mathrel{=}\textit{licond}\;(\lambda \_ \;\textit{x'}\to \textit{pr}\;\textit{x'})}$
. The bfilterAlg pr is essentially a bidirectional version of the function
${\textit{fcond}\;\textit{pr}\mathrel{=}\textit{licond}\;(\lambda \_ \;\textit{x'}\to \textit{pr}\;\textit{x'})}$
. The bfilterAlg pr is essentially a bidirectional version of the function
![]() ${\lambda \textit{x}\;\textit{xs}\to \mathbf{if}\;\textit{pr}\;\textit{x}\;\mathbf{then}\;\textit{x}\mathbin{:}\textit{xs}\;\mathbf{else}\;\textit{xs}}$
. One example of bfilter is the bfilter even defined in Section 3.2.
${\lambda \textit{x}\;\textit{xs}\to \mathbf{if}\;\textit{pr}\;\textit{x}\;\mathbf{then}\;\textit{x}\mathbin{:}\textit{xs}\;\mathbf{else}\;\textit{xs}}$
. One example of bfilter is the bfilter even defined in Section 3.2.
5.2 Bidirectional map
Map is another important high-order function in functional programming and program calculation, which applies a function to each element of a list. In this section, we will give three different definitions of bidirectional map with different source and view conditions. The first one is bmap, which is just a bidirectional map that preserves the length of the source and view list. It has no other constraints on the source and view. The second one is bmap’, which takes the constraint on individual elements of the list into consideration. The third one is bmapl (and bmapr), which goes a step further and takes into account the constraints on adjacent elements of the list as well. These three bidirectional versions of map cover a large range of applications. In particular, the most powerful bmapl is helpful in our later calculation of bidirectional maximum segment sum.
5.2.1 Bidirectional map: Preserving length
First, we give bmap which preserves the lengths of both source and view lists. It simply requires the parameter to have trivial contracts like bfoldr:

It is clear to see that if the change on the view does not change its length, after backward propagation through
![]() ${\textit{put}_{\textit{bmap}\;\ell}}$
, the length of the source will not be changed.
${\textit{put}_{\textit{bmap}\;\ell}}$
, the length of the source will not be changed.
As shown in Section 2.1, map is just a special version of fold. Similarly, we can also implement bmap using bfoldr’ as shown in Appendix B.2. One example of bmap is the bmap bhead defined in Section 3.2.
5.2.2 Bidirectional map: Preserving inner constraints
The above bmap assumes that the lens argument it takes never introduces any constraint. But this is not always the case. When the parameter lens has nontrivial contracts, the bidirectional map combinator should reflect these contracts in its result lens. Thus, we define another version of bidirectional map which takes the inner constraints on elements of lists into consideration:
The bmap’ simply lifts the contracts of its parameter to all elements in the source and view lists. As seen above, bmap’ is a generalized version of bmap; they are equivalent when the parameter lens
![]() ${\ell}$
has trivial contracts. Also, we can implement bmap’ using bfoldr’ in the same way as shown in Appendix B.2. One example of bmap’ is shown in Appendix C.2
${\ell}$
has trivial contracts. Also, we can implement bmap’ using bfoldr’ in the same way as shown in Appendix B.2. One example of bmap’ is shown in Appendix C.2
In the above definition of
![]() ${\textit{bmap'}\;\ell}$
, we directly use
${\textit{bmap'}\;\ell}$
, we directly use
![]() ${\textit{cs}_{\ell}}$
and
${\textit{cs}_{\ell}}$
and
![]() ${\textit{cv}_{\ell}}$
in the contracts of the result lens. The
${\textit{cv}_{\ell}}$
in the contracts of the result lens. The
![]() ${\textit{bmap'}\;\ell}$
has no requirement on the contracts of
${\textit{bmap'}\;\ell}$
has no requirement on the contracts of
![]() ${\ell}$
. Another alternative definition of bmap’ more similar to the definition of bfoldr’ which takes predicate parameters is as follows:
${\ell}$
. Another alternative definition of bmap’ more similar to the definition of bfoldr’ which takes predicate parameters is as follows:

We use the first definition in the paper as it takes fewer arguments.
5.2.3 Bidirectional map: Preserving constraints on adjacent elements
In practice, it is very common that map f is composed with a function that produces a list with some constraints on adjacent elements. For instance, map f may be composed with inits’, where the result of
![]() ${[\mskip1.5mu \textit{as}_{\mathrm{1}},\textit{as}_{\mathrm{2}},\ldots,\textit{as}_{\textit{n}}\mskip1.5mu]}$
produced by
${[\mskip1.5mu \textit{as}_{\mathrm{1}},\textit{as}_{\mathrm{2}},\ldots,\textit{as}_{\textit{n}}\mskip1.5mu]}$
produced by
![]() ${\textit{inits'}\;[\mskip1.5mu \textit{a}_{\mathrm{1}},\textit{a}_{\mathrm{2}},\ldots,\textit{a}_{\textit{n}}\mskip1.5mu]}$
has the constraint
${\textit{inits'}\;[\mskip1.5mu \textit{a}_{\mathrm{1}},\textit{a}_{\mathrm{2}},\ldots,\textit{a}_{\textit{n}}\mskip1.5mu]}$
has the constraint
![]() ${(\textit{init}\;\textit{as}_{\textit{i}}\mathrel{=}\textit{as}_{i-1})\;\land\;(\textit{init}\;\textit{as}_{\mathrm{1}}\mathrel{=}[\mskip1.5mu \mskip1.5mu])}$
.
${(\textit{init}\;\textit{as}_{\textit{i}}\mathrel{=}\textit{as}_{i-1})\;\land\;(\textit{init}\;\textit{as}_{\mathrm{1}}\mathrel{=}[\mskip1.5mu \mskip1.5mu])}$
.
In bidirectional programming, we need to carefully specify this kind of constraints. Recall the binits in Section 4.1 with the following view condition:
The composition
![]() ${\textit{binits};\textit{bmap}\;\ell}$
inviolates the condition in Definition 2. This motivated us to introduce bmapl, another bidirectional version of map which is able to express constraints on adjacent elements.
${\textit{binits};\textit{bmap}\;\ell}$
inviolates the condition in Definition 2. This motivated us to introduce bmapl, another bidirectional version of map which is able to express constraints on adjacent elements.
The core idea is that for
![]() ${\textit{bmap'}\;\ell}$
, we augment the parameter lens
${\textit{bmap'}\;\ell}$
, we augment the parameter lens
![]() ${\ell}$
of type
${\ell}$
of type
![]() ${\textit{S}\leftrightarrow\textit{V}}$
with an extra argument of type S representing the adjacent element, which leads to a parameterized lens
${\textit{S}\leftrightarrow\textit{V}}$
with an extra argument of type S representing the adjacent element, which leads to a parameterized lens
![]() ${\ell'\mathbin{:}\textit{S}\to (\textit{S}\leftrightarrow\textit{V})}$
. Notice that
${\ell'\mathbin{:}\textit{S}\to (\textit{S}\leftrightarrow\textit{V})}$
. Notice that
![]() ${\ell'}$
is still a bidirectional version of a function of type
${\ell'}$
is still a bidirectional version of a function of type
![]() ${\textit{S}\to \textit{V}}$
, so we need to restrict the get components of all
${\textit{S}\to \textit{V}}$
, so we need to restrict the get components of all
![]() ${\ell'\;\textit{s}}$
to be the same function for any
${\ell'\;\textit{s}}$
to be the same function for any
![]() ${\textit{s}\mathbin{:}\textit{S}}$
. We again use similar syntax to refinement types to express the requirement on the parameters and define the following syntactic sugar:
${\textit{s}\mathbin{:}\textit{S}}$
. We again use similar syntax to refinement types to express the requirement on the parameters and define the following syntactic sugar:
Our two syntactic sugars can be used nestedly:
The bidirectional map preserving constraints on adjacent elements is defined as follows:
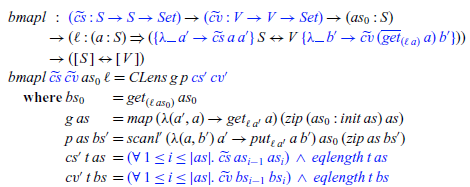
The constraints on adjacent elements of lists are specified by
![]() ${\widetilde {\textit{cs}}}$
and
${\widetilde {\textit{cs}}}$
and
![]() ${\widetilde {\textit{cv}}}$
. For example, if we take
${\widetilde {\textit{cv}}}$
. For example, if we take
![]() ${\widetilde {\textit{cs}}}$
to be
${\widetilde {\textit{cs}}}$
to be
![]() ${\lambda \textit{x}\;\textit{y}\to (\textit{init}\;\textit{y}\mathrel{=}\textit{x})}$
and
${\lambda \textit{x}\;\textit{y}\to (\textit{init}\;\textit{y}\mathrel{=}\textit{x})}$
and
![]() ${\textit{as}_{\mathrm{0}}} to be {[\mskip1.5mu \mskip1.5mu]}$
, then the source condition of the
${\textit{as}_{\mathrm{0}}} to be {[\mskip1.5mu \mskip1.5mu]}$
, then the source condition of the
![]() $ {\textit{bmapl}\;\textit{as}_{\mathrm{0}}\;\ell}$
is equivalent to
$ {\textit{bmapl}\;\textit{as}_{\mathrm{0}}\;\ell}$
is equivalent to
![]() ${\textit{cv}_{\textit{binits}}}$
, and thus, the composition
${\textit{cv}_{\textit{binits}}}$
, and thus, the composition
![]() ${\textit{binits};\textit{bmapl}\;[\mskip1.5mu \mskip1.5mu]\;\ell}$
is valid.
${\textit{binits};\textit{bmapl}\;[\mskip1.5mu \mskip1.5mu]\;\ell}$
is valid.
The implementation of
![]() ${\textit{bmapl}\;\textit{a}_{0}\;\ell}$
is visualized in Figure 1. The parameterized lens
${\textit{bmapl}\;\textit{a}_{0}\;\ell}$
is visualized in Figure 1. The parameterized lens
![]() ${\ell\mathbin{:}(\textit{a}\mathbin{:}\textit{S})\Rightarrow ({\{\lambda \_ \;\textit{a'}\to \widetilde {\textit{cs}}\;\textit{a}\;\textit{a'}\}}\;\textit{S}\leftrightarrow\textit{V}\;{\{\lambda \_ \;\textit{b'}\to \widetilde {\textit{cv}}\;(\overline{\textit{get}}_{(\ell\;\textit{a})}\;\textit{a})\;\textit{b'}\}})}$
takes the adjacent element of source as the argument. As we have mentioned in Section 4.1,
${\ell\mathbin{:}(\textit{a}\mathbin{:}\textit{S})\Rightarrow ({\{\lambda \_ \;\textit{a'}\to \widetilde {\textit{cs}}\;\textit{a}\;\textit{a'}\}}\;\textit{S}\leftrightarrow\textit{V}\;{\{\lambda \_ \;\textit{b'}\to \widetilde {\textit{cv}}\;(\overline{\textit{get}}_{(\ell\;\textit{a})}\;\textit{a})\;\textit{b'}\}})}$
takes the adjacent element of source as the argument. As we have mentioned in Section 4.1,
![]() ${\overline{\textit{get}}_{\ell\;\textit{a}}}$
means using the get component of
${\overline{\textit{get}}_{\ell\;\textit{a}}}$
means using the get component of
![]() ${\ell\;\textit{a}}$
simply as a total function. For the get direction, when computing
${\ell\;\textit{a}}$
simply as a total function. For the get direction, when computing
![]() ${\textit{b}_{\textit{i}}}$
from
${\textit{b}_{\textit{i}}}$
from
![]() ${\textit{a}_{\textit{i}}}$
, we pass the adjacent element
${\textit{a}_{\textit{i}}}$
, we pass the adjacent element
![]() ${\textit{a}_{i-1}}$
to
${\textit{a}_{i-1}}$
to
![]() ${\ell}$
and make sure that we have
${\ell}$
and make sure that we have
![]() ${\widetilde {\textit{cv}}\;\textit{b}_{i-1}\;\textit{b}_{\textit{i}}}$
, which ensures the view list satisfies the constraints on adjacent elements. For the put direction, when computing
${\widetilde {\textit{cv}}\;\textit{b}_{i-1}\;\textit{b}_{\textit{i}}}$
, which ensures the view list satisfies the constraints on adjacent elements. For the put direction, when computing
![]() ${a_i^\prime}$
from
${a_i^\prime}$
from
![]() ${b_i^\prime}$
and
${b_i^\prime}$
and
![]() ${\textit{a}_{\textit{i}}}$
, we pass
${\textit{a}_{\textit{i}}}$
, we pass
![]() ${\textit{a}_{i-1}'}$
to
${\textit{a}_{i-1}'}$
to
![]() ${\ell}$
and make sure that we have
${\ell}$
and make sure that we have
![]() ${\widetilde {\textit{cs}}\;\textit{a}_{i-1}'\;a_i^\prime}$
, which ensures the updated source list satisfies the constraints on adjacent elements.
${\widetilde {\textit{cs}}\;\textit{a}_{i-1}'\;a_i^\prime}$
, which ensures the updated source list satisfies the constraints on adjacent elements.
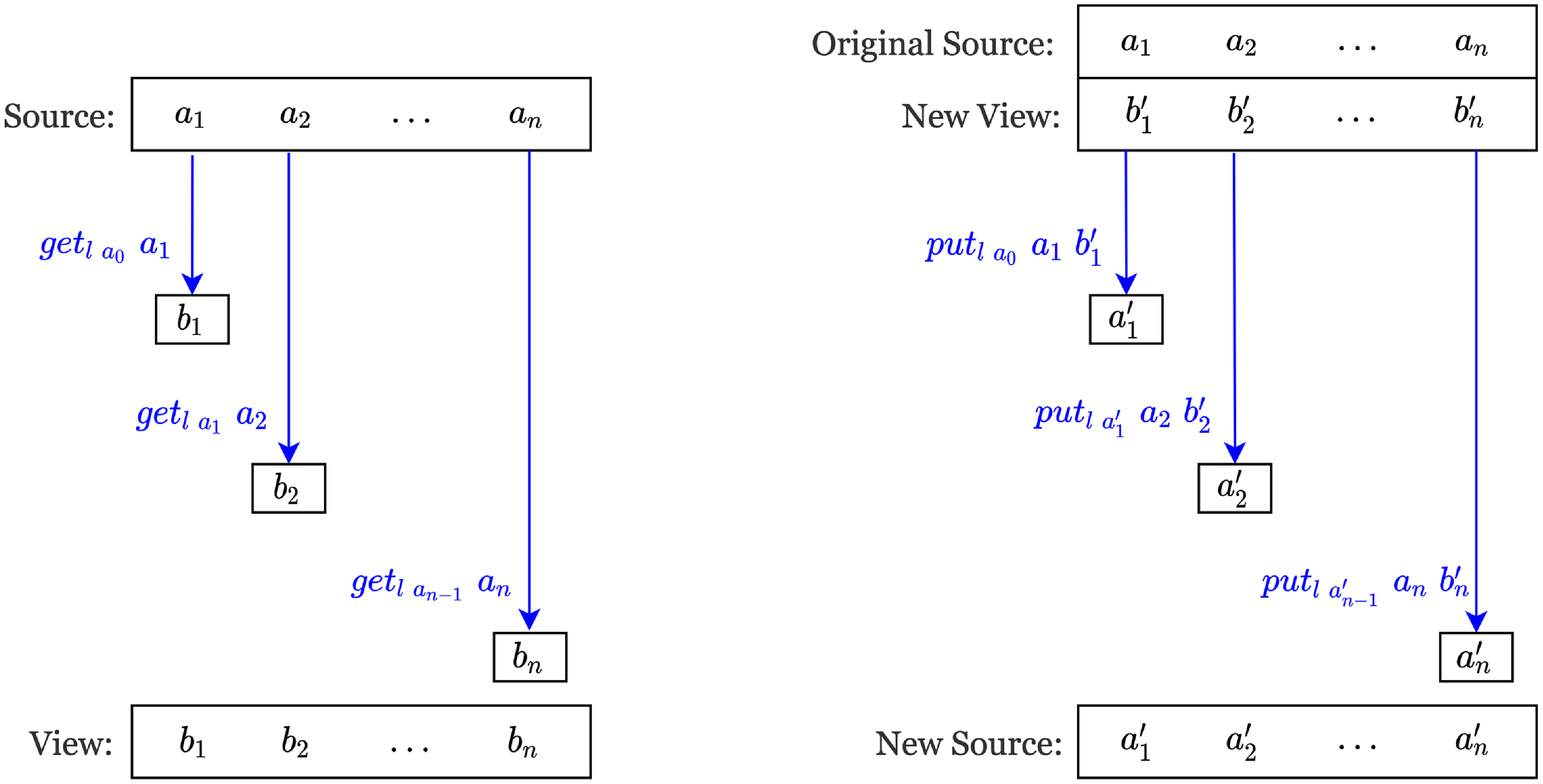
Fig. 1. Implementation of bmapl. The left figure shows the computation of the get and the right figure shows the computation of the put.
Note that we use the name bmapl because the constraints are leftward on every pair of
![]() ${\textit{a}_{i-1}}$
and
${\textit{a}_{i-1}}$
and
![]() ${\textit{a}_{\textit{i}}}$
. Similarly, we have a bmapr which are used to deal with constraints rightward on every pair of
${\textit{a}_{\textit{i}}}$
. Similarly, we have a bmapr which are used to deal with constraints rightward on every pair of
![]() ${\textit{a}_{\textit{i}}}$
and
${\textit{a}_{\textit{i}}}$
and
![]() ${\textit{a}_{i+1}}$
, usually generated by some
${\textit{a}_{i+1}}$
, usually generated by some
![]() ${\textit{scanr'}\;(\oplus)\;\textit{a}_{0}}$
. The implementation is almost the same except for replacing
${\textit{scanr'}\;(\oplus)\;\textit{a}_{0}}$
. The implementation is almost the same except for replacing
![]() ${\textit{scanl'}}$
in the code with
${\textit{scanl'}}$
in the code with
![]() ${\textit{scanr'}}$
. One example of bmapl is shown in Appendix C.3.
${\textit{scanr'}}$
. One example of bmapl is shown in Appendix C.3.
5.2.4 Bidirectional map using inner bidirectional fold
As we have seen so far,
![]() ${\textit{bmapl}\;\ell}$
is useful to give a bidirectional version for map f with expressive contraints. What if f is a fold? Since bmapl takes a parameterized lens of type
${\textit{bmapl}\;\ell}$
is useful to give a bidirectional version for map f with expressive contraints. What if f is a fold? Since bmapl takes a parameterized lens of type
![]() ${\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{V})}$
, we cannot directly pass either bfoldr or bfoldr’ to bmapl. Moreover, since the bidirectional fold we needed depends on the
${\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{V})}$
, we cannot directly pass either bfoldr or bfoldr’ to bmapl. Moreover, since the bidirectional fold we needed depends on the
![]() ${\widetilde {\textit{cs}}}$
in the source condition of the result of bmapl, it is actually difficult to give a general bidirectional fold. Fortunately, we can define some special bidirectional versions of fold to cope with some frequently used constraints, such as
${\widetilde {\textit{cs}}}$
in the source condition of the result of bmapl, it is actually difficult to give a general bidirectional fold. Fortunately, we can define some special bidirectional versions of fold to cope with some frequently used constraints, such as
![]() ${\lambda \textit{a}_{i-1}\;\textit{a}_{\textit{i}}\to \textit{init}\;\textit{a}_{\textit{i}}\mathrel{=}\textit{a}_{i-1}}$
. The
${\lambda \textit{a}_{i-1}\;\textit{a}_{\textit{i}}\to \textit{init}\;\textit{a}_{\textit{i}}\mathrel{=}\textit{a}_{i-1}}$
. The
![]() ${\textit{bfoldl}_{\textit{init}}}$
shown below is such a special
${\textit{bfoldl}_{\textit{init}}}$
shown below is such a special
![]() ${\textit{bfold}}$
that can be used inside bmapl:
${\textit{bfold}}$
that can be used inside bmapl:
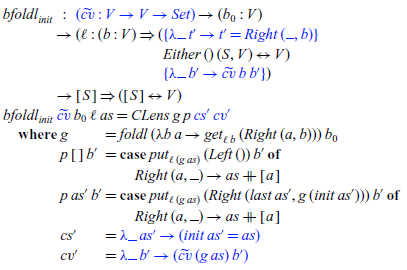
The
![]() ${\textit{bfoldl}_{\textit{init}}}$
takes a parameterized contract lens and returns another parameterized contract lens which is suitable to be passed to bmapl. Notice that the result parameterized lens
${\textit{bfoldl}_{\textit{init}}}$
takes a parameterized contract lens and returns another parameterized contract lens which is suitable to be passed to bmapl. Notice that the result parameterized lens
![]() ${\textit{bfoldl}_{\textit{init}}\;{\widetilde {\textit{cv}}}\;\textit{b}_{0}\;\ell}$
of type
${\textit{bfoldl}_{\textit{init}}\;{\widetilde {\textit{cv}}}\;\textit{b}_{0}\;\ell}$
of type
![]() ${[\mskip1.5mu \textit{S}\mskip1.5mu]\Rightarrow ([\mskip1.5mu \textit{S}\mskip1.5mu]\leftrightarrow\textit{V})}$
indeed has the same get component for any argument
${[\mskip1.5mu \textit{S}\mskip1.5mu]\Rightarrow ([\mskip1.5mu \textit{S}\mskip1.5mu]\leftrightarrow\textit{V})}$
indeed has the same get component for any argument
![]() ${\textit{as}\mathbin{:}[\mskip1.5mu \textit{S}\mskip1.5mu]}$
, because the get component does not use as at all. The get direction is a standard foldl, and the put direction only computes the last element of the new source list, since other elements are given as the argument indicated by the source condition
${\textit{as}\mathbin{:}[\mskip1.5mu \textit{S}\mskip1.5mu]}$
, because the get component does not use as at all. The get direction is a standard foldl, and the put direction only computes the last element of the new source list, since other elements are given as the argument indicated by the source condition
![]() ${{\lambda \_ \;\textit{as'}\to (\textit{init}\;\textit{as'}\mathrel{=}\textit{as})}}$
.
${{\lambda \_ \;\textit{as'}\to (\textit{init}\;\textit{as'}\mathrel{=}\textit{as})}}$
.
For an example usage of
![]() ${\textit{bfoldl}_{\textit{init}}}$
, we refer to Appendix C.4.
${\textit{bfoldl}_{\textit{init}}}$
, we refer to Appendix C.4.
5.3 Bidirectional scan
After discussing bidirectional fold and map, we turn to bidirectional scan, which is an efficient computation pattern using an accumulation parameter and is useful for optimization (as will be seen later). The main challenge to bidirectionalize scan is that the result of scan may have constraints between adjacent elements similar to bmapl. In this section, we give a powerful bidirectional version of scan with the help of contract lenses:

The implementation of
![]() ${\textit{bscanl}\;{\widetilde {\textit{cv}}}\;\textit{b}_{\mathrm{0}}\;\ell}$
is visualized in Figure 2. The get direction is a standard scanl’. For the put direction, when computing
${\textit{bscanl}\;{\widetilde {\textit{cv}}}\;\textit{b}_{\mathrm{0}}\;\ell}$
is visualized in Figure 2. The get direction is a standard scanl’. For the put direction, when computing
![]() ${a_i^\prime}$
from
${a_i^\prime}$
from
![]() ${\textit{a}_{\textit{i}}}$
and
${\textit{a}_{\textit{i}}}$
and
![]() ${b_i^\prime}$
, we pass
${b_i^\prime}$
, we pass
![]() ${\textit{b}_{i-1}'}$
to the lens
${\textit{b}_{i-1}'}$
to the lens
![]() ${\ell}$
to restrict the result of put is of form
${\ell}$
to restrict the result of put is of form
![]() ${\textit{Right}\;(_ ,\textit{b}_{i-1}')}$
.
${\textit{Right}\;(_ ,\textit{b}_{i-1}')}$
.
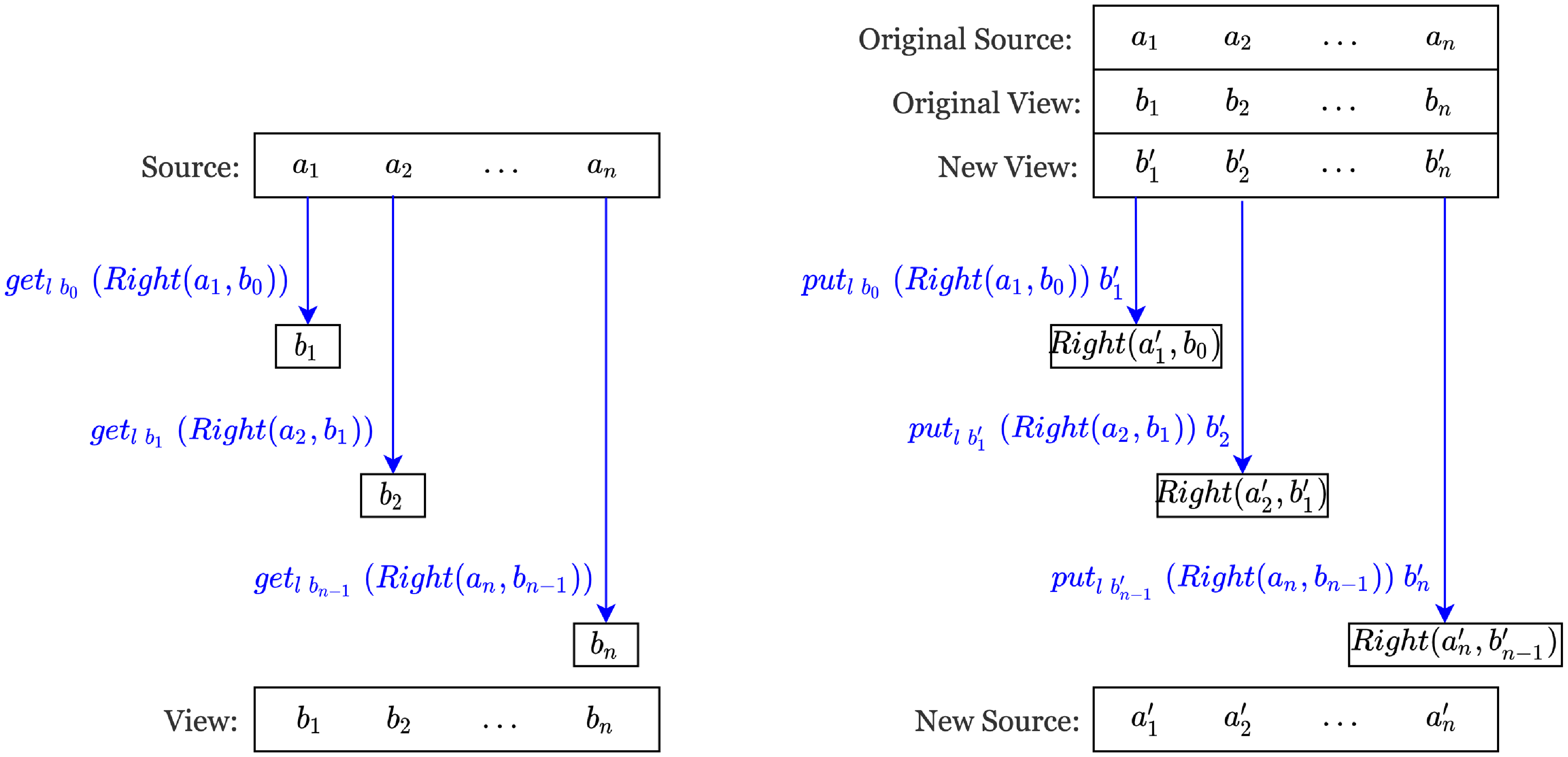
Fig. 2. Implementation of bscanl. The left figure shows the computation of the get and the right figure shows the computation of the put.
For an example usage of bscanl, we refer to Appendix C.5.
6 Bidirectional calculation laws
So far, we have seen that fundamental high-order functions such as fold, filter, map, and scan can be extended naturally from unidirectional to bidirectional, and that these bidirectional versions can be used to describe various bidirectional behaviors through suitable definitions of get, put, and the source/view conditions. In this section, we shall develop several important bidirectional calculation laws for manipulating them, including bidirectional versions of FOLD FUSION, Map Fusion, and Scan Lemma. These bidirectional calculation laws are useful to reason about and optimize bidirectional programs.
6.1 Bidirectional fold fusion
We start with a bidirectional version of the FOLD FUSION law for bfoldr. To characterize bidirectional fold fusion law, we first bidirectionalize the list functor
![]() ${\mathrm{F_L}}$
in Section 2.2:
${\mathrm{F_L}}$
in Section 2.2:

The tricky part lies in the last line above when there is a mismatch in the constructors of source and view. The implementation chooses a default value
![]() ${\textit{b}_{\mathrm{0}}}$
of type V to help with this process. With this bidirectional list functor, we can have the following bidirectional fold fusion law, which is similar to the unidirectional fold fusion law but with this explicit default value:
${\textit{b}_{\mathrm{0}}}$
of type V to help with this process. With this bidirectional list functor, we can have the following bidirectional fold fusion law, which is similar to the unidirectional fold fusion law but with this explicit default value:
It reads that the lens composition
![]() ${\textit{bfoldr}\;\ell_{\mathrm{1}};\ell}$
can be fused into a single lens
${\textit{bfoldr}\;\ell_{\mathrm{1}};\ell}$
can be fused into a single lens
![]() ${\textit{bfoldr}\;\ell_{\mathrm{2}}}$
if there exists
${\textit{bfoldr}\;\ell_{\mathrm{2}}}$
if there exists
![]() ${\ell_{\mathrm{2}}}$
such that the equation
${\ell_{\mathrm{2}}}$
such that the equation
![]() ${\ell_{\mathrm{1}};\ell\mathrel{=}\textit{blistF}\;(\textit{get}_{\ell_{\mathrm{1}}}\;(\textit{Left}\;()))\;\ell;\ell_{\mathrm{2}}}$
holds.
${\ell_{\mathrm{1}};\ell\mathrel{=}\textit{blistF}\;(\textit{get}_{\ell_{\mathrm{1}}}\;(\textit{Left}\;()))\;\ell;\ell_{\mathrm{2}}}$
holds.
Similarly, we have another fusion law for
![]() ${\textit{bfoldr'}}$
, for which we need a slightly different bidirectional version of the list functor
${\textit{bfoldr'}}$
, for which we need a slightly different bidirectional version of the list functor
![]() ${\mathrm{F_L}}$
. The good thing is that we do not need the default value anymore because the contracts of bfoldr’ guarantee that there will not be any mismatch:
${\mathrm{F_L}}$
. The good thing is that we do not need the default value anymore because the contracts of bfoldr’ guarantee that there will not be any mismatch:

Then, the fusion law is stated as:

6.2 Bidirectional map fusion
The bidirectional map fusion laws for bmap and bmap’ are quite easy since they just map
![]() ${\ell}$
to each element of the list in both forward and backward transformations. Since bmap is a special case of bmap’, we only give the bidirectional map fusion law for bmap’:
${\ell}$
to each element of the list in both forward and backward transformations. Since bmap is a special case of bmap’, we only give the bidirectional map fusion law for bmap’:
Similarly, we can give the bidirectional map fusion law for bmapl:
where
![]() ${(;;)}$
is the composition of parameterized lenses whose types are of form
${(;;)}$
is the composition of parameterized lenses whose types are of form
![]() ${\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{V})}$
. It is defined as follows:
${\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{V})}$
. It is defined as follows:

The definition of
![]() ${\ell_{\mathrm{1}};;\ell_{\mathrm{2}}}$
is quite intuitive. We just pass the parameter
${\ell_{\mathrm{1}};;\ell_{\mathrm{2}}}$
is quite intuitive. We just pass the parameter
![]() ${\textit{a}} to {\ell_{\mathrm{1}}}$
, and the result of a after the forward transformation of
${\textit{a}} to {\ell_{\mathrm{1}}}$
, and the result of a after the forward transformation of
![]() ${\ell_{\mathrm{1}}} to {\ell_{\mathrm{2}}}$
. Notice that we still use the syntactic sugar
${\ell_{\mathrm{1}}} to {\ell_{\mathrm{2}}}$
. Notice that we still use the syntactic sugar
![]() ${\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{T})}$
for the type of the result parameterized lenses, which means the
${\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{T})}$
for the type of the result parameterized lenses, which means the
![]() $ {\textit{get}}$
component is the same for any parameter. This makes natural sense because both
$ {\textit{get}}$
component is the same for any parameter. This makes natural sense because both
![]() ${\ell_{\mathrm{1}}}$
and
${\ell_{\mathrm{1}}}$
and
![]() ${\ell_{\mathrm{2}}}$
have fixed
${\ell_{\mathrm{2}}}$
have fixed
![]() ${\textit{get}}$
components. It is also easy to check that the composition
${\textit{get}}$
components. It is also easy to check that the composition
![]() ${\ell_{\mathrm{1}}\;\textit{a};\ell_{\mathrm{2}}\;(\textit{get}_{\ell_{\mathrm{1}}\;\textit{a}}\;\textit{a})}$
is well defined (i.e., satisfies the condition in Definition 2).
${\ell_{\mathrm{1}}\;\textit{a};\ell_{\mathrm{2}}\;(\textit{get}_{\ell_{\mathrm{1}}\;\textit{a}}\;\textit{a})}$
is well defined (i.e., satisfies the condition in Definition 2).
6.3 Bidirectional fold-map fusion
We give a bidirectional fold-map fusion law for bfoldr’ and bmap’, both of which preserve the length of the source list.
First, we bidirectionalize
![]() ${\mathrm{F_m}}$
defined in Section 2.2 with conditions required by bfoldr’:
${\mathrm{F_m}}$
defined in Section 2.2 with conditions required by bfoldr’:

The result of bmapF has the same source condition as the lens bfoldr’ takes. Now we can give the bidirectional fold-map fusion law for bfoldr’:
6.4 Bidirectional scan lemma
In the unidirectional world, the Scan Lemma is a special version of the FOLD FUSION law. Note that replacing inits with inits’ and scanl with scanl’, the scan lemma still holds. The major challenge for developing a similar bidirectional calculation law on contract lenses is that the inits’ introduces a constraint on adjacent elements of the view list. Fortunately, the contract-lens combinator bmapl can handle constraints on adjacent elements. With bmapl,
![]() ${\textit{bfoldl}_{\textit{init}}}$
, and
${\textit{bfoldl}_{\textit{init}}}$
, and
![]() ${\textit{bscanl}}$
, we can successfully obtain a bidirectional version of scan lemma:
${\textit{bscanl}}$
, we can successfully obtain a bidirectional version of scan lemma:
The form of the bidirectional scan lemma is quite similar to its unidirectional version modulo some administrative parameters for contracts. We give an example of Bidirectional Scan Lemma in Appendix C.6.
7 Examples
In this section, we will demonstrate further through three examples that with contract lenses, combinators, and associated calculation laws, we are able to flexibly construct and optimize bidirectional programs. The first example is a projection problem from geometry, where the conditions afforded by contract lenses are essential for its construction. The second example concerns bidirectional data conversion, specifically, string processing and formatting. It showcases that within our framework, such computation tasks can be constructed in a point-free style, of which efficiency is guaranteed by calculational laws. The third example stems from a classic scenario of program calculation, and it demonstrates the ability to reason about and optimize complicated bidirectional programs through semantics-preserving transformation based on calculational laws, in a way that one would have done for unidirectional programs.
7.1 Projection onto a hyperplane
Let us look at an example to see the expressive power of contract lenses, especially how we can use contracts to constrain the changes of source and view. One basic computation in the area of geometry is to calculate the projection of a point onto a hyperplane in a higher-dimensional Euclidean space. In this example, we want to synchronize a point
![]() $xs =[x_1, x_2, \dots, x_n]$
Footnote 11 in a n-dimensional Euclidean space with the projection of it onto the hyperplane
$xs =[x_1, x_2, \dots, x_n]$
Footnote 11 in a n-dimensional Euclidean space with the projection of it onto the hyperplane
![]() $H:\sum_{i=1}^n x_i = 0$
. The projection of X onto H is the point
$H:\sum_{i=1}^n x_i = 0$
. The projection of X onto H is the point
![]() $ys = [x_1 - m, x_2 - m,\dots, x_n - m]$
where
$ys = [x_1 - m, x_2 - m,\dots, x_n - m]$
where
![]() $m = \frac 1 n \sum_{i=1}^n x_i$
. What’s more, there is a unique hyperplane H’ parallel to H and through the point xs. We want an extra property that the new point obtained from backward transformation is on the hyperplane H’. In other words, the task is to synchronize a list of numbers with the differences between each number and the mean of all numbers; meanwhile, the mean of the source list is unchanged after changes on the view list.
$m = \frac 1 n \sum_{i=1}^n x_i$
. What’s more, there is a unique hyperplane H’ parallel to H and through the point xs. We want an extra property that the new point obtained from backward transformation is on the hyperplane H’. In other words, the task is to synchronize a list of numbers with the differences between each number and the mean of all numbers; meanwhile, the mean of the source list is unchanged after changes on the view list.
One way to implement this synchronization using lenses is to compose two lenses, where one lens synchronizes a list with a pair of the list itself and its mean, and the other lens synchronizes this pair with the list of differences. The constraints that the dimension n and the hyperplane H’ should not be changed can be easily expressed with contracts. The full implementation is as follows:

The specifications of synchronization behavior on each lenses are clearly expressed by contracts, which enables the compositions as we see in the definition of bproj.
7.2 String formatting and processing
Specifying programs that manipulate texts/strings bidirectionally is not new and has been extensively studied in Bohannon et al. (Reference Bohannon, Foster, Pierce, Pilkiewicz and Schmitt2008) and Reference Matsuda and WangMatsuda & Wang (2015b ). The novelty of our framework is that it supports a point-free style of specifications and calculational reasonings for such computational tasks.
7.2.1 String formatting
Let us look at the following string formatting task: given an input string, we want to filter out all digits and convert all remaining characters to upper case. With contract-lens combinators, we readily specify it in point-free style (for simplicity, we assume that characters in strings are either numbers or letters):

The composition is valid, since one can check that
![]() ${\textit{fcond}\;(not\,{\circ}\textit{isDigit})}$
and
${\textit{fcond}\;(not\,{\circ}\textit{isDigit})}$
and
![]() ${\textit{licond}\;(\lambda \_ \;\textit{c}\to not\;(\textit{isDigit}\;\textit{c}))}$
are by definition equivalent.
${\textit{licond}\;(\lambda \_ \;\textit{c}\to not\;(\textit{isDigit}\;\textit{c}))}$
are by definition equivalent.
In this naive specification, intermediate structures are created after one lens and are immediately consumed by another, in both directions. Recall that bfilter is an instance of bfoldr’, using Bfoldr’ Fusion, we reason as follows:

where

The definition of balg is not as complicated as it seems: it is essentially the combination of
![]() ${\textit{bfilterAlg}\;(not\,{\circ }\textit{isDigit})}$
and btoUpper.
${\textit{bfilterAlg}\;(not\,{\circ }\textit{isDigit})}$
and btoUpper.
It is easy to verify the condition of the Bfoldr’ Fusion law, which is the lens equivalence relation:
The calculated version creates no intermediate structure and hence is more efficient in practice.
7.2.2 String encoding and decoding
Another useful string processing algorithm is the encoding and decoding, which is usually used in compressing a string. It is very appropriate to write them as a single bidirectional program in order to make it easier to maintain and optimize the encoding and decoding algorithms at the same time (Matsuda &Wang, Reference Matsuda and Wang2020). Let us consider the following simple string encoding algorithm which illustrates the idea of Run Length Encoding:

For simplicity, the input string has already been splitted into a list of strings, where each string consists of consecutive identical characters. The compression compresses consecutive identical characters into its ASCII value and number of consecutive occurrences. The
![]() ${\textit{map}\;\textit{encode}}$
maps the consecutive identical characters to the pair of the character and the length. Then the
${\textit{map}\;\textit{encode}}$
maps the consecutive identical characters to the pair of the character and the length. Then the
![]() ${\textit{map}\;\textit{ascii}}$
transforms the characters to their ASCII values. Finally, the
${\textit{map}\;\textit{ascii}}$
transforms the characters to their ASCII values. Finally, the
![]() ${\textit{foldr'}\;\textit{cat}}$
concatenates the pairs to a single list. For example,Footnote 12
${\textit{foldr'}\;\textit{cat}}$
concatenates the pairs to a single list. For example,Footnote 12
Using the contract-lens combinators we defined in Section 5, it is easy to derive a bidirectional version of the function compression. The length of the results should not be changed; meanwhile, the ASCII values in the results should all be greater than or equal to 0 and less than 128. Thus, the view condition is defined as
![]() ${\textit{cv}_ {\textit{comp}}\;\textit{v}\;\textit{as}\mathrel{=}(|\textit{v}|=|\textit{as}|)\;\land\;(\forall\;\mathrm{1}\le\textit{i}\le|\textit{as}|,\textit{odd}\;\textit{i}\;\lor\;(\mathrm{0}\le\textit{as}_{\textit{i}}\mathbin{<}\mathrm{128}))}:$
${\textit{cv}_ {\textit{comp}}\;\textit{v}\;\textit{as}\mathrel{=}(|\textit{v}|=|\textit{as}|)\;\land\;(\forall\;\mathrm{1}\le\textit{i}\le|\textit{as}|,\textit{odd}\;\textit{i}\;\lor\;(\mathrm{0}\le\textit{as}_{\textit{i}}\mathbin{<}\mathrm{128}))}:$

where the following contract lenses are used:

It is easy to check the contract lens bcompression is well defined. However, this version of bcompress is not so efficient because it traverses the string three times. We can use the bidirectional calculation laws in Section 6 to reduce both the compression and the decompression algorithms to only one traversal simultaneously:

7.3 Bidirectional maximum segment sum
Now let us turn to another example involving more advanced program calculation. The maximum segment sum is a classic problem in the area of program calculation. To demonstrate the ability of our calculation framework, we change the specification of mss in Section 2.3 into a bidirectional version directly using contract-lens combinators and optimize it to a more efficient version which has time complexity O(n) in both get and put directions; meanwhile, the semantics is preserved.
To see this concretely, let us first get a bidirectional version of mss without considering efficiency. To achieve this, we introduce a refinement type
![]() ${\textit{TailsList}\;\textit{a}\mathrel{=}\{\textit{as}\mathbin{:}[\mskip1.5mu [\mskip1.5mu \textit{a}\mskip1.5mu]\mskip1.5mu]\mid (\forall\;\mathrm{1}\le\textit{i}\mathbin{<}\textit{n},\textit{tail}\;\textit{as}_{\textit{i}}\mathrel{=}\textit{as}_{i+1})\;\land\;(\textit{tail}\;\textit{as}_{\textit{n}}\mathrel{=}[\mskip1.5mu \mskip1.5mu])\}}$
. It is a modified version of the type
${\textit{TailsList}\;\textit{a}\mathrel{=}\{\textit{as}\mathbin{:}[\mskip1.5mu [\mskip1.5mu \textit{a}\mskip1.5mu]\mskip1.5mu]\mid (\forall\;\mathrm{1}\le\textit{i}\mathbin{<}\textit{n},\textit{tail}\;\textit{as}_{\textit{i}}\mathrel{=}\textit{as}_{i+1})\;\land\;(\textit{tail}\;\textit{as}_{\textit{n}}\mathrel{=}[\mskip1.5mu \mskip1.5mu])\}}$
. It is a modified version of the type
![]() ${[\mskip1.5mu [\mskip1.5mu \textit{a}\mskip1.5mu]\mskip1.5mu]}$
, where each element of the list is the tail of the previous element, and the tail of the last element is the empty list. The specification of the bidirectional version of mss is
${[\mskip1.5mu [\mskip1.5mu \textit{a}\mskip1.5mu]\mskip1.5mu]}$
, where each element of the list is the tail of the previous element, and the tail of the last element is the empty list. The specification of the bidirectional version of mss is

where the definitions of the contracts and contract lenses appeared are

The binits and bmaximum’ have been already defined in the previous sections. It is easy to check that bmss is well defined, that is, it satisfies round-tripping properties and the condition of lens composition.
Next, we make use of the bidirectional calculation rules we developed in Section 6 to optimize the bmss. The calculation goes as follows:

One thing worth noting is that in the third step of calculation, we use a specific bidirectional Horner’s rule:

The get direction of
![]() ${(\textit{btails}_{\textit{init}};;\textit{bmapSum};;\textit{bmaximum2})\;\textit{a}}$
for any
${(\textit{btails}_{\textit{init}};;\textit{bmapSum};;\textit{bmaximum2})\;\textit{a}}$
for any
![]() ${\textit{a}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]}$
is similar to the original Horner’s rule with
${\textit{a}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]}$
is similar to the original Horner’s rule with
![]() ${\otimes\mathrel{=}\mathbin{+}} and {\oplus\mathrel{=}\textit{max}}$
. It would take space to develop a general bidirectional Horner’s rule for any
${\otimes\mathrel{=}\mathbin{+}} and {\oplus\mathrel{=}\textit{max}}$
. It would take space to develop a general bidirectional Horner’s rule for any
![]() ${\oplus} and {\otimes}$
, because we require that and
${\oplus} and {\otimes}$
, because we require that and
![]() ${\otimes}$
form a ring structure and keep it in the bidirectional setting. However, it is useful to define and prove some specific bidirectional versions of the Horner’s rule like this.
${\otimes}$
form a ring structure and keep it in the bidirectional setting. However, it is useful to define and prove some specific bidirectional versions of the Horner’s rule like this.
By now, we have successfully derived a correct and linear-time efficient bidirectional program that can synchronize a list with its maximum segment sum.
Let us look at an example to get a better understanding of our final result
![]() ${\textit{bscanl}\;(\mathbin{-}\infty)\;\ell;\textit{bmaximum'}}$
that is visualized in Figure 3. Given the input list
${\textit{bscanl}\;(\mathbin{-}\infty)\;\ell;\textit{bmaximum'}}$
that is visualized in Figure 3. Given the input list
![]() ${\textit{xs}\mathrel{=}[\mskip1.5mu \mathrm{3},\mathbin{-}\mathrm{1},\mathrm{4},\mathbin{-}\mathrm{1},\mathrm{5},\mathbin{-}\mathrm{9}\mskip1.5mu]}, {\textit{get}_{\textit{bscanl}\;{\textit{ctrue}}\;(\mathbin{-}\infty)\;\ell}\;\textit{xs}}$
yields
${\textit{xs}\mathrel{=}[\mskip1.5mu \mathrm{3},\mathbin{-}\mathrm{1},\mathrm{4},\mathbin{-}\mathrm{1},\mathrm{5},\mathbin{-}\mathrm{9}\mskip1.5mu]}, {\textit{get}_{\textit{bscanl}\;{\textit{ctrue}}\;(\mathbin{-}\infty)\;\ell}\;\textit{xs}}$
yields
![]() ${[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{10},\mathrm{1}\mskip1.5mu]}$
, whose each element refers to the maximum segment sum ending at this position. Then,
${[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{10},\mathrm{1}\mskip1.5mu]}$
, whose each element refers to the maximum segment sum ending at this position. Then,
![]() ${\textit{get}_{\textit{bmaximum'}}\;[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{10},\mathrm{1}\mskip1.5mu]}$
yields 10, which is the maximum segment sum of the whole list. Now we change the result from
${\textit{get}_{\textit{bmaximum'}}\;[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{10},\mathrm{1}\mskip1.5mu]}$
yields 10, which is the maximum segment sum of the whole list. Now we change the result from
![]() ${\mathrm{10}} to {\mathrm{6}}$
. For the backward direction,
${\mathrm{10}} to {\mathrm{6}}$
. For the backward direction,
![]() ${\textit{put}_{\textit{bmaximum'}}\;[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{10},\mathrm{1}\mskip1.5mu]\;\mathrm{6}} yields {[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{6},\mathrm{1}\mskip1.5mu]}$
. Finally,
${\textit{put}_{\textit{bmaximum'}}\;[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{10},\mathrm{1}\mskip1.5mu]\;\mathrm{6}} yields {[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{6},\mathrm{1}\mskip1.5mu]}$
. Finally,
![]() ${\textit{put}_{\textit{bscanl}\;{\textit{ctrue}}\;(\mathbin{-}\infty)\;\ell}\;[\mskip1.5mu \mathrm{3},\mathbin{-}\mathrm{1},\mathrm{4},\mathbin{-}\mathrm{1},\mathrm{5},\mathbin{-}\mathrm{9}\mskip1.5mu]\;[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{6},\mathrm{1}\mskip1.5mu]} yields {[\mskip1.5mu \mathrm{3},\mathbin{-}\mathrm{1},\mathrm{4},\mathbin{-}\mathrm{1},\mathrm{1},\mathbin{-}\mathrm{5}\mskip1.5mu]}$
.
${\textit{put}_{\textit{bscanl}\;{\textit{ctrue}}\;(\mathbin{-}\infty)\;\ell}\;[\mskip1.5mu \mathrm{3},\mathbin{-}\mathrm{1},\mathrm{4},\mathbin{-}\mathrm{1},\mathrm{5},\mathbin{-}\mathrm{9}\mskip1.5mu]\;[\mskip1.5mu \mathrm{3},\mathrm{2},\mathrm{6},\mathrm{5},\mathrm{6},\mathrm{1}\mskip1.5mu]} yields {[\mskip1.5mu \mathrm{3},\mathbin{-}\mathrm{1},\mathrm{4},\mathbin{-}\mathrm{1},\mathrm{1},\mathbin{-}\mathrm{5}\mskip1.5mu]}$
.
Fig. 3. Visualization of an example calculation of bmss.
8 Related work
In this section, we discuss related work on partiality in the lens framework, Hoare-style reasoning of BX, automatic bidirectionalization, and some attempts on calculating with lenses.
8.1 Lens family and partiality of put
The most prominent approach to BX is the lens framework formally introduced by Foster et al. (Reference Foster, Greenwald, Moore, Pierce and Schmitt2007). It is highly influential and directly inspired a number of follow-on works including Boomerang (Bohannon et al., Reference Bohannon, Foster, Pierce, Pilkiewicz and Schmitt2008), quotient (Foster et al., Reference Foster, Pilkiewicz and Pierce2008), matching lenses (Barbosa et al., Reference Barbosa, Cretin, Foster, Greenberg and Pierce2010), symmetric lenses (Hofmann et al., Reference Hofmann, Pierce and Wagner2011), edit lenses (Hofmann et al., Reference Hofmann, Pierce and Wagner2012), BiGUL (Ko et al., Reference Ko, Zan and Hu2016), applicative lenses (Reference Matsuda and WangMatsuda & Wang, 2015a ), HOBiT (Matsuda & Wang, Reference Matsuda and Wang2018), and so on. The present paper on contract lenses is no exception. On the issue of partiality, different approaches were taken by the various works, which can be broadly categorized into the following.
8.1.1 Formulation of contracts and relation to type systems
As argued in Section 1.1, giving total definitions to get and put components is not always desirable, as the effort in achieving it necessarily complicates program design and reasoning. Some previous work on lenses ensures the totality of them by advanced type systems, with enriched type constraints over the type variables S, V in the lens type
![]() ${\textit{S}\leftrightarrow\textit{V}}$
. For example, in Foster et al. (Reference Foster, Greenwald, Moore, Pierce and Schmitt2007), partial lenses are ruled out by set-based type constraints that precisely characterize the domain/range of get and put, and in Boomerang (Bohannon et al., Reference Bohannon, Foster, Pierce, Pilkiewicz and Schmitt2008), the underlying String type is enriched with regular languages to serve as types for dictionary lenses.
${\textit{S}\leftrightarrow\textit{V}}$
. For example, in Foster et al. (Reference Foster, Greenwald, Moore, Pierce and Schmitt2007), partial lenses are ruled out by set-based type constraints that precisely characterize the domain/range of get and put, and in Boomerang (Bohannon et al., Reference Bohannon, Foster, Pierce, Pilkiewicz and Schmitt2008), the underlying String type is enriched with regular languages to serve as types for dictionary lenses.
As far as we know, lens formulations with enriched type systems like the above are not readily used to flexibly express the bidirectional behaviors we see in this paper. Take
![]() ${\textit{bmap}\mathbin{:}(\textit{S}\leftrightarrow\textit{V})\to [\mskip1.5mu \textit{S}\mskip1.5mu]\leftrightarrow[\mskip1.5mu \textit{V}\mskip1.5mu]}$
as an example. With contracts, we can easily ensure that the changes on view do not modify the length of lists by setting the view condition to eqlength. However, it is nontrivial to express the “equal length” view condition by only constraining the types S and V themselves, instead of specifying constraints on the changes of values of types S and V. By adding an additional parameter to bmap specifying the length of the source and view list, one could encode bmap indirectly with a notion of dependent/refinement types into something like the following:
${\textit{bmap}\mathbin{:}(\textit{S}\leftrightarrow\textit{V})\to [\mskip1.5mu \textit{S}\mskip1.5mu]\leftrightarrow[\mskip1.5mu \textit{V}\mskip1.5mu]}$
as an example. With contracts, we can easily ensure that the changes on view do not modify the length of lists by setting the view condition to eqlength. However, it is nontrivial to express the “equal length” view condition by only constraining the types S and V themselves, instead of specifying constraints on the changes of values of types S and V. By adding an additional parameter to bmap specifying the length of the source and view list, one could encode bmap indirectly with a notion of dependent/refinement types into something like the following:
This version of bmap fixes the length of lists, which is obviously less general than the versions using eqlength like the bmap in Section 5.2.1 and bmap’ in Section 5.2.2.
The “equal length” view condition is essentially a constraint on the dynamic changes of inputs to a lens, which can be nicely handled by our view contract. In our framework, contracts specifies the ranges that lens components behave well, the dynamic changes that a lens can reasonably accept, and the conditions that different components can compose together.
It is worth noting that different from the previous work on constraining the source and view types (Foster et al., Reference Foster, Greenwald, Moore, Pierce and Schmitt2007; Bohannon et al., Reference Bohannon, Foster, Pierce, Pilkiewicz and Schmitt2008), contracts are not part of types, but rather additional specifications that parallel get and put. Moreover, users have full control of these specifications, just as how they specify the component get and put in the first place. In this sense, user have the flexibility to choose different contracts based on the same underlying get and put. For instance, the “equal length” condition for bmap may be strengthened so that additionally the first element of the list is preserved. These choices are completely up to the users.
An alternative design choice of contract lenses is to encode the BackwardValidity and ForwardValidity laws as well as the extra conditions of the ConditionedPutget and ConditionedGetPut laws directly into the types of get and put with refinement types:
With the above refinement type signatures, we can use the original PUTGET and GETPUT laws of lenses. Note that the definition of contract lenses is still a four-tuple of get, put, cs, and cv in this case. There is no clear advantage or disadvantage between these two approaches. We choose to characterize the properties of contracts with explicit laws like BackwardValidity and ForwardValidity to avoid the complication of type signatures and emphasize the differences between traditional lenses and contract lenses.
In this work, we do not impose any restriction on the constraints used in contracts. It is the users’ work to prove the round-tripping properties of contract lenses and the well-definedness of lens composition by either handwritten proofs or formalization in theorem provers like Agda. As a result, the designer of a practical system that implements contract lenses has to strike a balance between expressiveness of contracts and checkability of contracts implications. Nonetheless, we believe such systems are implementable, by restricting the set of contracts available to users to a small set of efficiently solvable constraints. As shown in our examples, simple predicates like eqlength can already help with constructing powerful combinators like generic mapping over lists.
8.1.2 Edit lenses
Edit lenses (Hofmann et al., Reference Hofmann, Pierce and Wagner2012) model changes to view/source as operations (edits) in contrast to states in the traditional lenses. The edits are represented as monoids, and monoid actions on set become the actions of applying an edit to a state. As a result, only the edits in the monoid are allowed to be applied to the states, which in a way restricts changes to the source and view. But unlike contract lenses, these restrictions are not used to address partiality; in fact, edit lenses have the same problem of partiality as state-based ones because the monoid actions are allowed to be partial. For example, the edit del which deletes the last element of a list is partial as we cannot apply it to an empty list. Extra dynamic checks are needed to ensure that the computation of edit lenses will not fail. For contract lenses, the get and put will not fail as long as the source conditions and view conditions are satisfied.
8.1.3 Totality with Maybe monad
Another approach is to wrap the return type of get and put in the Maybe monad to remove partiality (Reference Matsuda and WangMatsuda & Wang, 2015a
; Ko et al., Reference Ko, Zan and Hu2016; Xia et al., 2019). The put direction is a total function of type
![]() ${\textit{s}\to \textit{v}\to \textit{Maybe}\;\textit{s}}$
, and it returns Nothing at run-time when an invalid input is passed to it. This approach is unsuitable for program calculation as it lacks the ability to reason about partiality statically. We want to know the static specification of a program and get meaning results instead of just getting a Nothing when the program fails. Moreover, the specification can guide the design of program calculation laws.
${\textit{s}\to \textit{v}\to \textit{Maybe}\;\textit{s}}$
, and it returns Nothing at run-time when an invalid input is passed to it. This approach is unsuitable for program calculation as it lacks the ability to reason about partiality statically. We want to know the static specification of a program and get meaning results instead of just getting a Nothing when the program fails. Moreover, the specification can guide the design of program calculation laws.
8.1.4 Other discussions
The properties of partial BX and the relations between them are discussed extensively in Stevens (Reference Stevens2014). Different from our goal, the discussion there does not concern practical program construction nor mentions composition of transformations. In contrast, we focus on lenses that satisfy the round-tripping property on possibly partial domains. We make partiality explicit as a component of lenses and use it to explore composition behavior of partial lenses.
8.2 Hoare-style reasoning of bidirectional transformation
In Ko & Hu (Reference Ko and Hu2018), a reasoning framework for BiGUL programs based on Hoare logic is proposed, which is able to precisely characterize the bidirectional behaviors by reasoning in the put direction. The main concept is the put triplet in the form of
![]() $\{R\} b \{R'\}$
, which includes a set of pre- and post-conditions that are used to reason about the behavior of put in a way similar to the Hoare logic: if the original source s and the updated view v satisfy the precondition R, then
$\{R\} b \{R'\}$
, which includes a set of pre- and post-conditions that are used to reason about the behavior of put in a way similar to the Hoare logic: if the original source s and the updated view v satisfy the precondition R, then
![]() ${\textit{put}_{\textit{b}}\;\textit{s}\;\textit{v}}$
will produce an updated source satisfying the post-condition R’.
${\textit{put}_{\textit{b}}\;\textit{s}\;\textit{v}}$
will produce an updated source satisfying the post-condition R’.
To some extent, their pre- and post-conditions serve a similar purpose to our BackwardValidity law: if the original source s and the updated view v satisfy the view condition cv (get s) v, then put s v will successfully produce an updated source satisfying the source condition cs s (put s v). However, the novelty of contract lenses does not solely rely on the BackwardValidity law but also the combination with other three laws of the round-tripping properties which give a clear specification of lenses to resolve the partiality problem and make the composition of contract lenses easy and well-behaved. It is worth mentioning that in their framework, reasoning about lens composition is difficult and involves several complicated proof rules. In contrast, contract lenses make such reasoning easy: two lenses
![]() ${\ell_{\mathrm{1}}\mathbin{:}\{\textit{cs}_{\ell_{\mathrm{1}}}\}\;\textit{S}\leftrightarrow\textit{V}\;\{\textit{cv}_{\ell_{\mathrm{1}}}\}}$
and
${\ell_{\mathrm{1}}\mathbin{:}\{\textit{cs}_{\ell_{\mathrm{1}}}\}\;\textit{S}\leftrightarrow\textit{V}\;\{\textit{cv}_{\ell_{\mathrm{1}}}\}}$
and
![]() ${\ell_{\mathrm{2}}\mathbin{:}\{\textit{cs}_{\ell_{\mathrm{2}}}\}\;\textit{V}\leftrightarrow\textit{T}\;\{\textit{cv}_{\ell_{\mathrm{2}}}\}}$
can be composed into a lens
${\ell_{\mathrm{2}}\mathbin{:}\{\textit{cs}_{\ell_{\mathrm{2}}}\}\;\textit{V}\leftrightarrow\textit{T}\;\{\textit{cv}_{\ell_{\mathrm{2}}}\}}$
can be composed into a lens
![]() ${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\{\textit{cs}_{\ell_{\mathrm{1}}}\}\;\textit{S}\leftrightarrow\textit{T}\;\{\textit{cv}_{\ell_{\mathrm{2}}}\}} $
given the condition proposed in Definition 2.
${\ell_{\mathrm{1}};\ell_{\mathrm{2}}\mathbin{:}\{\textit{cs}_{\ell_{\mathrm{1}}}\}\;\textit{S}\leftrightarrow\textit{T}\;\{\textit{cv}_{\ell_{\mathrm{2}}}\}} $
given the condition proposed in Definition 2.
Furthermore, the purpose of pre- and post-conditions differs from that of source and view conditions. While pre- and post-conditions mainly focus on specifying the behaviors of the put components, our primary objective is to address the partiality problem of lenses, which allows for straightforward design of lenses and calculation laws.
8.3 Bidirectionalization
Bidirectionalization is an approach to bidirectional programming that is different from the lens framework. Instead of writing bidirectional programs directly in a specialized language, it aims to mechanically convert existing unidirectional programs into bidirectional ones. Voigtländer (Reference Voigtländer2009) gives a high-order function bff that receives a polymorphic get function and returns its put counterpart. The technique is extended (Voigtländer et al., Reference Voigtländer, Hu, Matsuda and Wang2010) by combining it with syntactic bidirectionalization (Matsuda et al., Reference Matsuda, Hu, Nakano, Hamana and Takeichi2007), which separates view changes in shape and in content. However, bidirectionalization is done for whole programs which lacks modular reasoning of compositions and therefore is not suitable for program calculation.
8.4 Calculating with lenses
The goal of generic point-free lenses (Pacheco & Cunha, Reference Pacheco and Cunha2010) is the most similar to ours. In that work, lens combinators are designed for many traditional high-order functions including fold and map. Subsequently, the point-free lenses are used for a limited form of calculation where the universal property (uniqueness) of the lens version of fold was proved and used to establish some program calculation laws for lenses such as the
![]() ${\textit{fold}}-{\textit{map}}$
fusion (Pacheco & Cunha, Reference Pacheco and Cunha2011).
${\textit{fold}}-{\textit{map}}$
fusion (Pacheco & Cunha, Reference Pacheco and Cunha2011).
But very different from ours, their work is based on the traditional lenses without contracts, which means that the problem of partiality seriously limits the composition of lenses. As a result, many crucial calculation laws such as the Scan Lemma are not expressible in their framework.
9 Formalization with Agda
In this section, we briefly discuss one possible formalization of contract lenses in Agda. We use this formalisation to prove the correctness of lens composition, all lens combinators, all calculation laws, and most of the examples (except the string processing example in Section 7.2) in this paper. As mentioned in Section 1.2, our intention is not to restrict potential users of contract lenses within this formalization but rather to provide a calculation framework which allows any method of reasoning. This Agda formalization shows one potential way to mechanize our framework.
The formalization of the whole contract lens calculation framework is rather straight-forward. A contract lens is a (possibly mutually defined) four-tuple get, put, cs, and cv, with a set of laws on them. This construction is formalized faithfully in the Agda code, where we define the lens type as a record type:

Typically, to construct an instance of this type, one will first define the four-tuple and then give proof of the four laws.
The formalization of lens combinators also follows from what we have in the paper. For instance, the bmap combinator with type
is formalized in Agda using existential types as:
One difference between our Agda formalization and what we have in the paper is that the Agda formalization does not use the syntactic sugar
![]() ${\ell\mathbin{:}\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{V})}$
defined in Section 5.2.3 to restrict the parameterized lens
${\ell\mathbin{:}\textit{S}\Rightarrow (\textit{S}\leftrightarrow\textit{V})}$
defined in Section 5.2.3 to restrict the parameterized lens
![]() ${\ell}$
to have a fixed get component. Instead, it defines
${\ell}$
to have a fixed get component. Instead, it defines
![]() ${\ell}$
as a lens of type
${\ell}$
as a lens of type
![]() ${(\textit{S},\textit{S})\leftrightarrow(\textit{V},\textit{V})}$
, where the parameter is embedded into the first component of the source pair. The former form is more clear and suitable for human reading, while the latter form is easier to formalize. We provided a translation between these two kinds of lenses and proved its correctness in the Agda formalization.
${(\textit{S},\textit{S})\leftrightarrow(\textit{V},\textit{V})}$
, where the parameter is embedded into the first component of the source pair. The former form is more clear and suitable for human reading, while the latter form is easier to formalize. We provided a translation between these two kinds of lenses and proved its correctness in the Agda formalization.
For the calculation part of this framework, we defined an equivalence relation between lenses of the above type as described in Definition 3. We also prove the congruence theorem for high-order lenses. Take bmap, for example, we prove that if
![]() ${\ell_{\mathrm{1}}\;\sim\ell_{\mathrm{2}}}$
, then
${\ell_{\mathrm{1}}\;\sim\ell_{\mathrm{2}}}$
, then
![]() ${\textit{bmap}\;\ell_{1}\;\sim\textit{bmap}\;\ell_{2}}$
. Our calculation laws are defined as theorems stating equivalences of lenses.
${\textit{bmap}\;\ell_{1}\;\sim\textit{bmap}\;\ell_{2}}$
. Our calculation laws are defined as theorems stating equivalences of lenses.
10 Conclusion
In this work, we propose a framework based on program calculation to enable the development of complex but efficient BX programs that are correct by construction. As part of the framework, we design a novel extension to lenses, contract lenses, for handling partiality and use it to justify general composition of lenses. Based on this, we extend the theories for program calculation to BX programming by designing combinators to capture bidirectional recursive computation patterns and proving their properties. We look at the list datatype and give proofs for fundamental calculation laws including various fusion laws for bidirectional fold and map and the bidirectional scan lemma. We showcase the construction of a realistic projection program, the derivation of efficient bidirectional string processing programs, and the maximum segment sum program to demonstrate the effectiveness of our framework.
This work focuses on the calculation for BXs on lists, which mirrors the classic work on the theory of list (Reference BirdBird, 1989a , 1987) in the literature of program calculation. Generalizing this bidirectional program calculation framework to algebraic datatypes generated by polynomial functors is a natural next step. Another possible future work is to design practical systems based on contract lenses to reason about and optimize BXs, automating the verification of round-tripping properties and lens composition using Satisfiability Modulo Theories (SMT) solvers.
Conflict of Interest
None.
A Calculating with total lenses
It is possible to make bmap total:

The additional parameter
![]() ${\textit{a}_{0}}$
is used as a default source value.
${\textit{a}_{0}}$
is used as a default source value.
One can develop an associated map fusion law for it:
However, this law requires
![]() ${\textit{get}_{\ell_{1}}\;\textit{a}_{0}\mathrel{=}\textit{b}_{0}}$
, a semantic condition on default values, which is an unwanted proof obligation to program calculators and optimizers.
${\textit{get}_{\ell_{1}}\;\textit{a}_{0}\mathrel{=}\textit{b}_{0}}$
, a semantic condition on default values, which is an unwanted proof obligation to program calculators and optimizers.
B Equivalent implementation of combinators
This appendix shows the code for equivalent implementations of some contract-lens combinators in Section 5.
B.1 Efficient bfoldr
This section shows an efficient implementation of bfoldr:

B.2 Implementation of bmap and bmap’ with bfoldr’
This section shows how to use bfoldr’ to implement bmap and bmap’:

C Examples for combinators
This appendix shows examples for some contract-lens combinators and calculation laws in Sections 5 and 6.
13.1 Computation instances of bmaximum
This section shows two calculation instances of the bmaximum example in Section 5.1. Let us assume that
![]() ${\textit{get}_{\textit{bmaximum}}\;[\mskip1.5mu \mathrm{9},\mathrm{2},\mathrm{5}\mskip1.5mu]}$
yields 9, and suppose that the output 9 is changed to 4. Now the following calculation shows how this change is reflected back to the input
${\textit{get}_{\textit{bmaximum}}\;[\mskip1.5mu \mathrm{9},\mathrm{2},\mathrm{5}\mskip1.5mu]}$
yields 9, and suppose that the output 9 is changed to 4. Now the following calculation shows how this change is reflected back to the input
![]() ${[\mskip1.5mu \mathrm{9},\mathrm{2},\mathrm{5}\mskip1.5mu]}$
and get
${[\mskip1.5mu \mathrm{9},\mathrm{2},\mathrm{5}\mskip1.5mu]}$
and get
![]() ${[\mskip1.5mu \mathrm{4},\mathrm{2},\mathrm{4}\mskip1.5mu]}$
:
${[\mskip1.5mu \mathrm{4},\mathrm{2},\mathrm{4}\mskip1.5mu]}$
:

Also, we can change the output 9 to a bigger value such as 10 and put it back to the input [9, 2, 5], which is shown in the following calculation:

C.2 Example of bmap’
The following defines a bidirectional version for
![]() ${\textit{map}\;(\mathbin{*}\mathrm{2})\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\to [\mskip1.5mu \textit{Int}\mskip1.5mu]}$
where the result list only contains even numbers:
${\textit{map}\;(\mathbin{*}\mathrm{2})\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\to [\mskip1.5mu \textit{Int}\mskip1.5mu]}$
where the result list only contains even numbers:

C.3 Example of bmapl
With the help of bmapl, we are able to handle any constraint on adjacent elements of a list, such as partial order relations. Consider a unidirectional computation
![]() ${\textit{map}\;(\lambda \textit{x}\to \textit{mod}\;\textit{x}\;\mathrm{10})\,{\circ }\textit{sort}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\to [\mskip1.5mu \textit{Int}\mskip1.5mu]}$
, which sorts the list first and then applies the modulo 10 operation on each element. The sort can be bidirectionalized as follows using some auxiliary functions from the Data.List module of Haskell:
${\textit{map}\;(\lambda \textit{x}\to \textit{mod}\;\textit{x}\;\mathrm{10})\,{\circ }\textit{sort}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\to [\mskip1.5mu \textit{Int}\mskip1.5mu]}$
, which sorts the list first and then applies the modulo 10 operation on each element. The sort can be bidirectionalized as follows using some auxiliary functions from the Data.List module of Haskell:

Thus, the backward transformation of
![]() ${\textit{map}\;(\lambda \textit{x}\to \textit{mod}\;\textit{x}\;\mathrm{10})}$
should produce a sorted list. With the help of bmapl, we can write a bidirectional version for
${\textit{map}\;(\lambda \textit{x}\to \textit{mod}\;\textit{x}\;\mathrm{10})}$
should produce a sorted list. With the help of bmapl, we can write a bidirectional version for
![]() ${\textit{map}\;(\lambda \textit{x}\to \textit{mod}\;\textit{x}\;\mathrm{10})}$
as follows:
${\textit{map}\;(\lambda \textit{x}\to \textit{mod}\;\textit{x}\;\mathrm{10})}$
as follows:

Now we have
![]() ${\textit{bsort};\textit{bmapl}\;(\mathbin{-}\infty)\;\textit{bmod10}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\leftrightarrow[\mskip1.5mu \textit{Int}\mskip1.5mu]}$
which synchronizes a list with the result list of each element modulo 10 after it is sorted.
${\textit{bsort};\textit{bmapl}\;(\mathbin{-}\infty)\;\textit{bmod10}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\leftrightarrow[\mskip1.5mu \textit{Int}\mskip1.5mu]}$
which synchronizes a list with the result list of each element modulo 10 after it is sorted.
C.4 Example of
 ${\textit{bfoldl}_{\textit{init}}}$
${\textit{bfoldl}_{\textit{init}}}$
In this example, we give a bidirectional version of the computation of prefix sums. An intuitive implementation of prefix sums is
![]() ${\textit{map}\;(\textit{foldl}\;(\mathbin{+})\;\mathrm{0})\,{\circ}\textit{inits}}$
. With the help of bmapl and
${\textit{map}\;(\textit{foldl}\;(\mathbin{+})\;\mathrm{0})\,{\circ}\textit{inits}}$
. With the help of bmapl and
![]() ${\textit{bfoldl}_{\textit{init}}}$
, we can easily bidirectionalize it as:
${\textit{bfoldl}_{\textit{init}}}$
, we can easily bidirectionalize it as:
where the badd is defined as:

This implementation of bidirectional prefix sum fits our intuition that a list of integers is isomorphic to its prefix sums. For example,
![]() ${\textit{get}_{\textit{bprefixSum}}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]}$
yields
${\textit{get}_{\textit{bprefixSum}}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]}$
yields
![]() ${[\mskip1.5mu \mathrm{1},\mathrm{3},\mathrm{6}\mskip1.5mu]}$
, and
${[\mskip1.5mu \mathrm{1},\mathrm{3},\mathrm{6}\mskip1.5mu]}$
, and
![]() ${\textit{put}_{\textit{bprefixSum}}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]\;[\mskip1.5mu \mathrm{4},\mathrm{6},\mathrm{8}\mskip1.5mu]}$
yields
${\textit{put}_{\textit{bprefixSum}}\;[\mskip1.5mu \mathrm{1},\mathrm{2},\mathrm{3}\mskip1.5mu]\;[\mskip1.5mu \mathrm{4},\mathrm{6},\mathrm{8}\mskip1.5mu]}$
yields
![]() ${[\mskip1.5mu \mathrm{4},\mathrm{2},\mathrm{2}\mskip1.5mu]}$
regardless of what the original list is.
${[\mskip1.5mu \mathrm{4},\mathrm{2},\mathrm{2}\mskip1.5mu]}$
regardless of what the original list is.
This is a good example showing the expressive power of contract lenses in writing specifications solving bidirectional programming problems: we can decompose a complex bidirectional problem into subproblems and solve them independently. With the help of contracts (source and view conditions), they can be composed safely to solve the original problem.
C.5 Example of bscanl
Consider that we want to synchronize a list of integers with its prefix products. The forward transformation is characterized by
![]() ${\textit{prefixProd}\mathrel{=}\textit{scanl'}\;(\mathbin{*})\;\mathrm{1}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\to [\mskip1.5mu \textit{Int}\mskip1.5mu]}$
. Note that there is a constraint on the adjacent elements of the view list: the preceding element divides the following element. This constraint can be expressed with the help of bscanl:
${\textit{prefixProd}\mathrel{=}\textit{scanl'}\;(\mathbin{*})\;\mathrm{1}\mathbin{:}[\mskip1.5mu \textit{Int}\mskip1.5mu]\to [\mskip1.5mu \textit{Int}\mskip1.5mu]}$
. Note that there is a constraint on the adjacent elements of the view list: the preceding element divides the following element. This constraint can be expressed with the help of bscanl:

C.6 Example of bidirectional scan lemma
We give a simple example which makes use of the Bidirectional Scan Lemma to derive an efficient bidirectional program from an inefficient one. Recall the bprefixSum defined in Appendix C.4 for calculating the prefix sums of a list. It has time complexity
![]() $O(n^2)$
. Applying the Bidirectional Scan Lemma to it, we can derive
$O(n^2)$
. Applying the Bidirectional Scan Lemma to it, we can derive
![]() ${\textit{bscanl}\;{\textit{ctrue}}\;\mathrm{0}\;\textit{badd}}$
, which has time complexity O(n) in both forward and backward transformations.
${\textit{bscanl}\;{\textit{ctrue}}\;\mathrm{0}\;\textit{badd}}$
, which has time complexity O(n) in both forward and backward transformations.



Discussions
No Discussions have been published for this article.