Journal Description
Vibration
Vibration
is a peer-reviewed, open access journal of vibration science and engineering, published quarterly online by MDPI.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, ESCI (Web of Science), and other databases.
- Journal Rank: CiteScore - Q2 (Engineering (miscellaneous))
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 29.3 days after submission; acceptance to publication is undertaken in 2.9 days (median values for papers published in this journal in the second half of 2024).
- Recognition of Reviewers: reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any MDPI journal, in appreciation of the work done.
Impact Factor:
1.9 (2023);
5-Year Impact Factor:
2.0 (2023)
Latest Articles
Soil–Structure Interaction and Damping by the Soil—Effects of Foundation Groups, Foundation Flexibility, Soil Stiffness and Layers
Vibration 2025, 8(1), 5; https://doi.org/10.3390/vibration8010005 (registering DOI) - 31 Jan 2025
Abstract
In many tasks of railway vibration, the structure, that is, the track, a bridge, and a nearby building and its floors, is coupled to the soil, and the soil–structure interaction and the damping by the soil should be included in the analysis to
[...] Read more.
In many tasks of railway vibration, the structure, that is, the track, a bridge, and a nearby building and its floors, is coupled to the soil, and the soil–structure interaction and the damping by the soil should be included in the analysis to obtain realistic resonance frequencies and amplitudes. The stiffness and damping of a variety of foundations is calculated by an indirect boundary element method which uses fundamental solutions, is meshless, uses collocation points on the boundary, and solves the singularity by an appropriate averaging over a part of the surface. The boundary element method is coupled with the finite element method in the case of flexible foundations such as beams, plates, piles, and railway tracks. The results, the frequency-dependent stiffness and damping of single and groups of rigid foundations on homogeneous and layered soil and the amplitude and phase of the dynamic compliance of flexible foundations, show that the simple constant stiffness and damping values of a rigid footing on homogeneous soil are often misleading and do not represent well the reality. The damping may be higher in some special cases, but, in most cases, the damping is lower than expected from the simple theory. Some applications and measurements demonstrate the importance of the correct damping by the soil.
Full article
Open AccessArticle
Experiment-Based Design of Stirling Cryocooler Compressor Using Response-Controlled Testing
by
Suna Güçyılmaz Çetin, Taylan Karaağaçlı and Ahmet H. Ertas
Vibration 2025, 8(1), 4; https://doi.org/10.3390/vibration8010004 - 30 Jan 2025
Abstract
Flexure-based Stirling cryocooler compressors are a critical technology in providing cryogenic temperatures in various advanced engineering fields, such as aerospace, defense, and medical imaging. The most challenging problem in the design of this type of compressor is achieving a precise alignment that preserves
[...] Read more.
Flexure-based Stirling cryocooler compressors are a critical technology in providing cryogenic temperatures in various advanced engineering fields, such as aerospace, defense, and medical imaging. The most challenging problem in the design of this type of compressor is achieving a precise alignment that preserves small gaps between the components moving relative to each other and avoids severe friction and wear. This paper introduces a novel experimental procedure for designing Stirling cryocooler compressors, leveraging a recently developed nonlinear experimental modal analysis method known as response-controlled stepped-sine testing (RCT). The alignment in a compressor prototype was significantly improved in light of a series of RCT with base excitation. The enhanced compressor design was subsequently validated though a series of constant-current tests, which confirmed the elimination of the sticking/locking phenomenon observed in the initial design. Furthermore, an indirect harmonic force surface (HFS)-based approach proposed for weakly nonlinear systems was extended to identify the high and nonlinear damping (up to a 65% hysteretic modal damping ratio) observed in the enhanced compressor design due to excessive friction. As another contribution, it was shown that the extrapolation of the HFS gives accurate results in the prediction of the nonlinear modal parameters at response levels where no experimental data are available. In light of these findings, it was concluded that the enhanced design needs further design modifications to further decrease the friction and wear between the moving parts. Overall, this study provides valuable insights for designing cryocooler compressors, with implications for aerospace and medical applications.
Full article
(This article belongs to the Special Issue Vibration Damping)
►▼
Show Figures
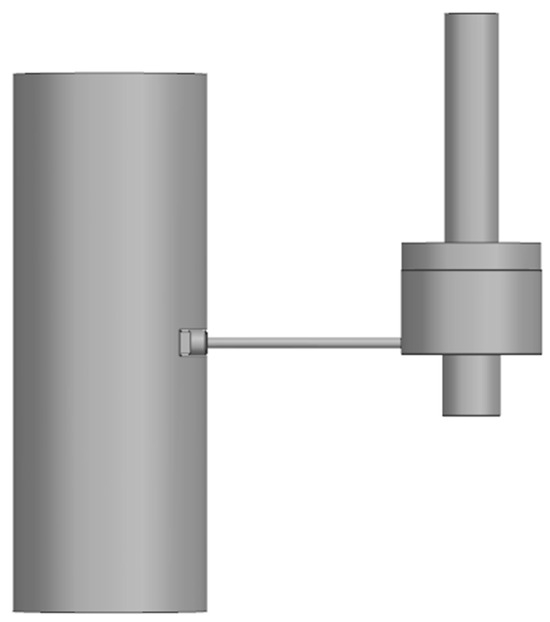
Figure 1
Figure 1
<p>Split linear Stirling cryocooler.</p> Full article ">Figure 2
<p>Flexure bearings used in Stirling cryocooler compressors.</p> Full article ">Figure 3
<p>(<b>a</b>) Small gaps in a typical flexure-based Stirling cryocooler; (<b>b</b>) flexure bearing.</p> Full article ">Figure 4
<p>Experiment-based design procedure for flexure-based Stirling cryocooler compressors.</p> Full article ">Figure 5
<p>Experimental setup for preliminary compressor prototype.</p> Full article ">Figure 6
<p>Harmonic responses of the piston measured during constant-current sine tests of the preliminary compressor prototype conducted at 1 A amplitude level and different excitation frequencies.</p> Full article ">Figure 7
<p>Considerable wear at the inner face of the magnet holder due to friction between the magnet holder and the cylinder.</p> Full article ">Figure 8
<p>Simplified models of the preliminary compressor prototype: (<b>a</b>) System A; (<b>b</b>) System B; (<b>c</b>) System C; (<b>d</b>) System D.</p> Full article ">Figure 9
<p>Response-controlled testing with base excitation.</p> Full article ">Figure 10
<p>Quasi-linear FRFs measured by response-controlled testing with base excitation: (<b>a</b>) System A; (<b>b</b>) System B; (<b>c</b>) System C.</p> Full article ">Figure 11
<p>Natural frequencies and viscous modal damping ratios identified from measured quasi-linear FRFs of simplified compressor models.</p> Full article ">Figure 12
<p>A simplified model corresponding to the enhanced compressor design: (<b>a</b>) schematic view; (<b>b</b>) response-controlled test configuration.</p> Full article ">Figure 13
<p>Natural frequency and viscous modal damping ratio obtained from quasi-linear FRFs of simplified model corresponding to the enhanced compressor design.</p> Full article ">Figure 14
<p>(<b>a</b>) Schematic view of the enhanced compressor design; (<b>b</b>) enhanced flexure bearing design.</p> Full article ">Figure 15
<p>Experimental setup for the enhanced compressor design.</p> Full article ">Figure 16
<p>(<b>a</b>) Frequency response curves measured from constant-current tests; (<b>b</b>) HFS constructed from measured frequency response curves.</p> Full article ">Figure 17
<p>Constant-response FRFs extracted by cutting the HFS with constant-displacement amplitude planes.</p> Full article ">Figure 18
<p>Variation in the nonlinear modal parameters of the enhanced compressor prototype with respect to the response level: (<b>a</b>) natural frequency; (<b>b</b>) modal damping ratio.</p> Full article ">Figure 19
<p>Variation in the modal constant of the enhanced compressor prototype with respect to the response level.</p> Full article ">Figure 20
<p>Comparison of the constant-current frequency response curves synthesized by using the identified nonlinear modal parameters with the ones directly measured by constant-current sine tests.</p> Full article ">Figure 21
<p>Extrapolated HFS.</p> Full article ">Figure 22
<p>Variation in the nonlinear modal parameters obtained from the extrapolated HFS: (<b>a</b>) natural frequency; (<b>b</b>) modal damping ratio.</p> Full article ">Figure 23
<p>Variation in the modal constant obtained from the extrapolated HFS.</p> Full article ">Figure 24
<p>Comparison of the constant-current frequency response curves synthesized by using the nonlinear modal parameters identified from the extrapolated HFS with the ones directly measured by constant-current sine tests.</p> Full article ">
<p>Split linear Stirling cryocooler.</p> Full article ">Figure 2
<p>Flexure bearings used in Stirling cryocooler compressors.</p> Full article ">Figure 3
<p>(<b>a</b>) Small gaps in a typical flexure-based Stirling cryocooler; (<b>b</b>) flexure bearing.</p> Full article ">Figure 4
<p>Experiment-based design procedure for flexure-based Stirling cryocooler compressors.</p> Full article ">Figure 5
<p>Experimental setup for preliminary compressor prototype.</p> Full article ">Figure 6
<p>Harmonic responses of the piston measured during constant-current sine tests of the preliminary compressor prototype conducted at 1 A amplitude level and different excitation frequencies.</p> Full article ">Figure 7
<p>Considerable wear at the inner face of the magnet holder due to friction between the magnet holder and the cylinder.</p> Full article ">Figure 8
<p>Simplified models of the preliminary compressor prototype: (<b>a</b>) System A; (<b>b</b>) System B; (<b>c</b>) System C; (<b>d</b>) System D.</p> Full article ">Figure 9
<p>Response-controlled testing with base excitation.</p> Full article ">Figure 10
<p>Quasi-linear FRFs measured by response-controlled testing with base excitation: (<b>a</b>) System A; (<b>b</b>) System B; (<b>c</b>) System C.</p> Full article ">Figure 11
<p>Natural frequencies and viscous modal damping ratios identified from measured quasi-linear FRFs of simplified compressor models.</p> Full article ">Figure 12
<p>A simplified model corresponding to the enhanced compressor design: (<b>a</b>) schematic view; (<b>b</b>) response-controlled test configuration.</p> Full article ">Figure 13
<p>Natural frequency and viscous modal damping ratio obtained from quasi-linear FRFs of simplified model corresponding to the enhanced compressor design.</p> Full article ">Figure 14
<p>(<b>a</b>) Schematic view of the enhanced compressor design; (<b>b</b>) enhanced flexure bearing design.</p> Full article ">Figure 15
<p>Experimental setup for the enhanced compressor design.</p> Full article ">Figure 16
<p>(<b>a</b>) Frequency response curves measured from constant-current tests; (<b>b</b>) HFS constructed from measured frequency response curves.</p> Full article ">Figure 17
<p>Constant-response FRFs extracted by cutting the HFS with constant-displacement amplitude planes.</p> Full article ">Figure 18
<p>Variation in the nonlinear modal parameters of the enhanced compressor prototype with respect to the response level: (<b>a</b>) natural frequency; (<b>b</b>) modal damping ratio.</p> Full article ">Figure 19
<p>Variation in the modal constant of the enhanced compressor prototype with respect to the response level.</p> Full article ">Figure 20
<p>Comparison of the constant-current frequency response curves synthesized by using the identified nonlinear modal parameters with the ones directly measured by constant-current sine tests.</p> Full article ">Figure 21
<p>Extrapolated HFS.</p> Full article ">Figure 22
<p>Variation in the nonlinear modal parameters obtained from the extrapolated HFS: (<b>a</b>) natural frequency; (<b>b</b>) modal damping ratio.</p> Full article ">Figure 23
<p>Variation in the modal constant obtained from the extrapolated HFS.</p> Full article ">Figure 24
<p>Comparison of the constant-current frequency response curves synthesized by using the nonlinear modal parameters identified from the extrapolated HFS with the ones directly measured by constant-current sine tests.</p> Full article ">
Open AccessArticle
Methodology for Designing Vibration Devices with Asymmetric Oscillations and a Given Value of the Asymmetry of the Driving Force
by
Mihail D. Gerasimov, Nickolai S. Lubimyi, Andrey A. Polshin, Boris S. Chetverikov and Anastasia Chetverikova
Vibration 2025, 8(1), 3; https://doi.org/10.3390/vibration8010003 - 15 Jan 2025
Abstract
In mechanical engineering, the building industry, and many other branches of industry, vibration machines are widely used, in which circular and directed oscillations predominate in the form of movement of the working equipment. This article examines methods for generating asymmetric oscillations, which are
[...] Read more.
In mechanical engineering, the building industry, and many other branches of industry, vibration machines are widely used, in which circular and directed oscillations predominate in the form of movement of the working equipment. This article examines methods for generating asymmetric oscillations, which are estimated by a numerical parameter, namely by the coefficient of asymmetry of the magnitude of the driving force when changing the direction of action in a directed motion within each period of oscillations. It is shown that for generating asymmetric mechanical vibrations, vibration devices are used, consisting of vibrators of directed vibrations, called stages. These stages form the total asymmetric driving force. The behavior of the total driving force of asymmetric vibrations and the working equipment of the vibration machine are described by analytical equations, which represent certain laws of motion of the mechanical system. This article presents a numerical analysis of methods for obtaining laws of motion for a two-stage, three-stage, and four-stage vibration device with asymmetric oscillations. An analysis of the methodology for obtaining a generalized law of motion for a vibration device with asymmetric oscillations is performed based on the application of polyharmonic oscillation synthesis methods. It is shown that the method of forming the total driving force of a vibration device based on the coefficients of the terms of the Fourier series has limited capabilities. This article develops, substantiates, and presents a generalized method for calculating and designing a vibration device with asymmetric oscillations by the value of the total driving force and a given value of the asymmetry coefficient in a wide range of rational designs of vibration machines. The proposed method is accompanied by a numerical example for a vibration device with an asymmetry coefficient of the total driving force equal to 10.
Full article
(This article belongs to the Special Issue Nonlinear Vibration of Mechanical Systems)
►▼
Show Figures
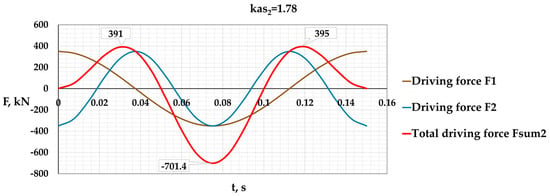
Figure 1
Figure 1
<p>Adding two (<span class="html-italic">F</span><sub>1</sub> and <span class="html-italic">F</span><sub>2</sub>) directed oscillations to obtain the total oscillation by initial conditions [<a href="#B31-vibration-08-00003" class="html-bibr">31</a>]. The asymmetry coefficient of the driving force is <math display="inline"><semantics> <mrow> <msub> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mn>2</mn> </mrow> </msub> <mo>=</mo> <mi>k</mi> </mrow> <mrow> <mi>d</mi> <mn>2</mn> </mrow> </msub> <mo>=</mo> <mn>1.78</mn> </mrow> </semantics></math>, (<span class="html-italic">F<sub>sum</sub></span><sub>2</sub>).</p> Full article ">Figure 2
<p>Addition of three directional oscillations (<span class="html-italic">F</span><sub>1</sub> and <span class="html-italic">F</span><sub>2</sub>, <span class="html-italic">F</span><sub>3</sub>) to obtain a total oscillation (<span class="html-italic">F<sub>sum</sub></span><sub>3</sub>) with asymmetry of the driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mn>3</mn> </mrow> </msub> <mo>=</mo> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>d</mi> <mn>3</mn> </mrow> </msub> <mo>=</mo> <mn>3.0</mn> </mrow> </semantics></math>, [<a href="#B46-vibration-08-00003" class="html-bibr">46</a>].</p> Full article ">Figure 3
<p>Addition of four directional oscillations (<span class="html-italic">F</span><sub>1</sub> and <span class="html-italic">F</span><sub>2</sub>, <span class="html-italic">F</span><sub>3</sub>, <span class="html-italic">F</span><sub>4</sub>) to obtain a total oscillation with asymmetry of the driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>d</mi> </mrow> </msub> <mo>=</mo> <mn>4.0</mn> </mrow> </semantics></math>, (<math display="inline"><semantics> <mrow> <msub> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mn>4</mn> </mrow> </msub> <mo>=</mo> <mi>k</mi> </mrow> <mrow> <mi>d</mi> <mn>4</mn> </mrow> </msub> <mo>=</mo> <mn>3.89</mn> </mrow> </semantics></math>, (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> <mn>4</mn> </mrow> </msub> </mrow> </semantics></math>)).</p> Full article ">Figure 4
<p>Graph of the change in the asymmetry coefficient (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mi>n</mi> </mrow> </msub> </mrow> </semantics></math>) of the total driving force of the vibration device, formed on the basis of the terms of the Fourier series of the function <math display="inline"><semantics> <mrow> <mo>=</mo> <msup> <mrow> <mi>c</mi> <mi>o</mi> <mi>s</mi> </mrow> <mrow> <mn>12</mn> </mrow> </msup> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>x</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> </mrow> </semantics></math> for the first six terms (<span class="html-italic">n</span> = 1…6).</p> Full article ">Figure 5
<p>A diagram of a vibration mechanism consisting of <span class="html-italic">n</span> pairs of unbalanced vibrators, each pair of which forms a vibration block, a stage that generates directed oscillations.</p> Full article ">Figure 6
<p>Support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>.</p> Full article ">Figure 7
<p>The sum of support reactions of all seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>.</p> Full article ">Figure 8
<p>Support reactions of each of the seven pairs of vibrators with coefficients <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> <mi>i</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, calculated using Equation (26).</p> Full article ">Figure 9
<p>The sum of support reactions of all seven pairs of vibrators with coefficients <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, calculated using Equation (26).</p> Full article ">Figure 10
<p>Fejer kernel, (<b>a</b>) is for N = 7, (<b>b</b>) is for several Fejer kernels [<a href="#B39-vibration-08-00003" class="html-bibr">39</a>,<a href="#B40-vibration-08-00003" class="html-bibr">40</a>,<a href="#B41-vibration-08-00003" class="html-bibr">41</a>].</p> Full article ">Figure 11
<p>Calculation of simplexes in the process of determining the optimal values of parameters <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mn>1</mn> </mrow> </msub> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msub> </mrow> </semantics></math>.</p> Full article ">Figure 12
<p>Values of parameters at the vertices of simplexes and the corresponding values of the dynamic coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>d</mi> </mrow> </msub> </mrow> </semantics></math>.</p> Full article ">Figure 13
<p>Calculation graphs of the magnitude of the driving forces of a vibration device with asymmetric oscillations with the total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 10 kN and the specified asymmetry coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> </mrow> </msub> </mrow> </semantics></math> = 7.0. (<b>a</b>) is support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 1 kN and the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>b</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>c</b>) is the support reactions of each of the seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, (<b>d</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 13 Cont.
<p>Calculation graphs of the magnitude of the driving forces of a vibration device with asymmetric oscillations with the total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 10 kN and the specified asymmetry coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> </mrow> </msub> </mrow> </semantics></math> = 7.0. (<b>a</b>) is support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 1 kN and the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>b</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>c</b>) is the support reactions of each of the seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, (<b>d</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 13 Cont.
<p>Calculation graphs of the magnitude of the driving forces of a vibration device with asymmetric oscillations with the total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 10 kN and the specified asymmetry coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> </mrow> </msub> </mrow> </semantics></math> = 7.0. (<b>a</b>) is support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 1 kN and the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>b</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>c</b>) is the support reactions of each of the seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, (<b>d</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 14
<p>Graph of change in total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> <mo>=</mo> <mi>f</mi> <mo>(</mo> <mi>t</mi> <mo>)</mo> </mrow> </semantics></math>.</p> Full article ">Figure 15
<p>(<b>a</b>) The test bench with synchronized pairs of imbalances for multi-stage production of asymmetric oscillations: 1 is a base, 2 is a body, 3 is a guide rod, 4 is the sliders, 5 is the imbalances, 6 is a driving force sensor. (<b>b</b>) A driving force magnitude recording sensor.</p> Full article ">
<p>Adding two (<span class="html-italic">F</span><sub>1</sub> and <span class="html-italic">F</span><sub>2</sub>) directed oscillations to obtain the total oscillation by initial conditions [<a href="#B31-vibration-08-00003" class="html-bibr">31</a>]. The asymmetry coefficient of the driving force is <math display="inline"><semantics> <mrow> <msub> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mn>2</mn> </mrow> </msub> <mo>=</mo> <mi>k</mi> </mrow> <mrow> <mi>d</mi> <mn>2</mn> </mrow> </msub> <mo>=</mo> <mn>1.78</mn> </mrow> </semantics></math>, (<span class="html-italic">F<sub>sum</sub></span><sub>2</sub>).</p> Full article ">Figure 2
<p>Addition of three directional oscillations (<span class="html-italic">F</span><sub>1</sub> and <span class="html-italic">F</span><sub>2</sub>, <span class="html-italic">F</span><sub>3</sub>) to obtain a total oscillation (<span class="html-italic">F<sub>sum</sub></span><sub>3</sub>) with asymmetry of the driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mn>3</mn> </mrow> </msub> <mo>=</mo> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>d</mi> <mn>3</mn> </mrow> </msub> <mo>=</mo> <mn>3.0</mn> </mrow> </semantics></math>, [<a href="#B46-vibration-08-00003" class="html-bibr">46</a>].</p> Full article ">Figure 3
<p>Addition of four directional oscillations (<span class="html-italic">F</span><sub>1</sub> and <span class="html-italic">F</span><sub>2</sub>, <span class="html-italic">F</span><sub>3</sub>, <span class="html-italic">F</span><sub>4</sub>) to obtain a total oscillation with asymmetry of the driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>d</mi> </mrow> </msub> <mo>=</mo> <mn>4.0</mn> </mrow> </semantics></math>, (<math display="inline"><semantics> <mrow> <msub> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mn>4</mn> </mrow> </msub> <mo>=</mo> <mi>k</mi> </mrow> <mrow> <mi>d</mi> <mn>4</mn> </mrow> </msub> <mo>=</mo> <mn>3.89</mn> </mrow> </semantics></math>, (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> <mn>4</mn> </mrow> </msub> </mrow> </semantics></math>)).</p> Full article ">Figure 4
<p>Graph of the change in the asymmetry coefficient (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> <mi>n</mi> </mrow> </msub> </mrow> </semantics></math>) of the total driving force of the vibration device, formed on the basis of the terms of the Fourier series of the function <math display="inline"><semantics> <mrow> <mo>=</mo> <msup> <mrow> <mi>c</mi> <mi>o</mi> <mi>s</mi> </mrow> <mrow> <mn>12</mn> </mrow> </msup> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>x</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> </mrow> </semantics></math> for the first six terms (<span class="html-italic">n</span> = 1…6).</p> Full article ">Figure 5
<p>A diagram of a vibration mechanism consisting of <span class="html-italic">n</span> pairs of unbalanced vibrators, each pair of which forms a vibration block, a stage that generates directed oscillations.</p> Full article ">Figure 6
<p>Support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>.</p> Full article ">Figure 7
<p>The sum of support reactions of all seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>.</p> Full article ">Figure 8
<p>Support reactions of each of the seven pairs of vibrators with coefficients <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> <mi>i</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, calculated using Equation (26).</p> Full article ">Figure 9
<p>The sum of support reactions of all seven pairs of vibrators with coefficients <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mi>k</mi> </mrow> </msub> <mo>=</mo> <mn>1.0</mn> </mrow> </semantics></math> and initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, calculated using Equation (26).</p> Full article ">Figure 10
<p>Fejer kernel, (<b>a</b>) is for N = 7, (<b>b</b>) is for several Fejer kernels [<a href="#B39-vibration-08-00003" class="html-bibr">39</a>,<a href="#B40-vibration-08-00003" class="html-bibr">40</a>,<a href="#B41-vibration-08-00003" class="html-bibr">41</a>].</p> Full article ">Figure 11
<p>Calculation of simplexes in the process of determining the optimal values of parameters <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mn>1</mn> </mrow> </msub> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>a</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msub> </mrow> </semantics></math>.</p> Full article ">Figure 12
<p>Values of parameters at the vertices of simplexes and the corresponding values of the dynamic coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>d</mi> </mrow> </msub> </mrow> </semantics></math>.</p> Full article ">Figure 13
<p>Calculation graphs of the magnitude of the driving forces of a vibration device with asymmetric oscillations with the total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 10 kN and the specified asymmetry coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> </mrow> </msub> </mrow> </semantics></math> = 7.0. (<b>a</b>) is support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 1 kN and the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>b</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>c</b>) is the support reactions of each of the seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, (<b>d</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 13 Cont.
<p>Calculation graphs of the magnitude of the driving forces of a vibration device with asymmetric oscillations with the total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 10 kN and the specified asymmetry coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> </mrow> </msub> </mrow> </semantics></math> = 7.0. (<b>a</b>) is support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 1 kN and the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>b</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>c</b>) is the support reactions of each of the seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, (<b>d</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 13 Cont.
<p>Calculation graphs of the magnitude of the driving forces of a vibration device with asymmetric oscillations with the total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 10 kN and the specified asymmetry coefficient <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>k</mi> </mrow> <mrow> <mi>a</mi> <mi>s</mi> </mrow> </msub> </mrow> </semantics></math> = 7.0. (<b>a</b>) is support reactions of each of the seven pairs of vibrators with the value <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> </mrow> </semantics></math> = 1 kN and the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>b</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>; (<b>c</b>) is the support reactions of each of the seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>, (<b>d</b>) is the sum of the support reactions of all seven pairs of vibrators with the initial phases <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>φ</mi> </mrow> <mrow> <mi>k</mi> <mn>0</mn> </mrow> </msub> <mo>=</mo> <mstyle scriptlevel="0" displaystyle="true"> <mfrac> <mrow> <mi>π</mi> </mrow> <mrow> <mn>2</mn> </mrow> </mfrac> </mstyle> <mrow> <mo>(</mo> <mi>k</mi> <mo>−</mo> <mn>1</mn> <mo>)</mo> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 14
<p>Graph of change in total driving force <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>F</mi> </mrow> <mrow> <mi>s</mi> <mi>u</mi> <mi>m</mi> </mrow> </msub> <mo>=</mo> <mi>f</mi> <mo>(</mo> <mi>t</mi> <mo>)</mo> </mrow> </semantics></math>.</p> Full article ">Figure 15
<p>(<b>a</b>) The test bench with synchronized pairs of imbalances for multi-stage production of asymmetric oscillations: 1 is a base, 2 is a body, 3 is a guide rod, 4 is the sliders, 5 is the imbalances, 6 is a driving force sensor. (<b>b</b>) A driving force magnitude recording sensor.</p> Full article ">
Open AccessArticle
Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials
by
Kadir Gunaydin, Orhan Gülcan and Aykut Tamer
Vibration 2025, 8(1), 2; https://doi.org/10.3390/vibration8010002 - 13 Jan 2025
Abstract
►▼
Show Figures
Different additive manufacturing modalities enable the production of multi-material components which can be used in a wide range of industrial applications. The prediction of the mechanical properties of these components via finite element modelling rather than through testing is critical in terms of
[...] Read more.
Different additive manufacturing modalities enable the production of multi-material components which can be used in a wide range of industrial applications. The prediction of the mechanical properties of these components via finite element modelling rather than through testing is critical in terms of cost and time. However, due to the higher computational time spent on the modelling of lattice structures, different methods have been investigated to accurately predict mechanical properties. For this purpose, this study proposes the use of a homogenization method in the two most common types of multi-material lattices: honeycomb and re-entrant auxetics. Modal analyses were performed, and the first six mode shapes were extracted from explicit and implicit models. The results were compared in terms of mode shapes and natural frequencies. The results showed that homogenization can be successfully applied to multi-material honeycomb and re-entrant auxetic lattices without compromising the accuracy. It was shown that the implicit models predict the natural frequencies with an error range of less than 6.5% when compared with the explicit models in all of the mode shapes for both honeycomb and re-entrant auxetic lattices. The Modal Assurance Criteria, which is an indication of the degree of similarity between the mode shapes of explicit and implicit models, was found to be higher than 0.996, indicating very high similarity.
Full article
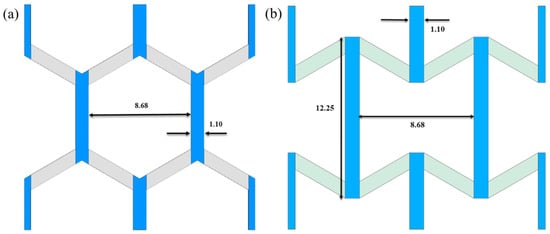
Figure 1
Figure 1
<p>Unit cell topologies: (<b>a</b>) honeycomb, (<b>b</b>) re-entrant. Units are in mm.</p> Full article ">Figure 2
<p>Elastic modulus convergence plot in z direction for honeycomb lattice structure.</p> Full article ">Figure 3
<p>Test articles: (<b>a</b>) honeycomb, (<b>b</b>) re-entrant.</p> Full article ">Figure 4
<p>Meshed unit cells: (<b>a</b>) honeycomb, (<b>b</b>) re-entrant.</p> Full article ">Figure 5
<p>Meshed lattice structures: (<b>a</b>) honeycomb explicit, (<b>b</b>) honeycomb implicit, (<b>c</b>) re-entrant explicit, (<b>d</b>) re-entrant implicit.</p> Full article ">
<p>Unit cell topologies: (<b>a</b>) honeycomb, (<b>b</b>) re-entrant. Units are in mm.</p> Full article ">Figure 2
<p>Elastic modulus convergence plot in z direction for honeycomb lattice structure.</p> Full article ">Figure 3
<p>Test articles: (<b>a</b>) honeycomb, (<b>b</b>) re-entrant.</p> Full article ">Figure 4
<p>Meshed unit cells: (<b>a</b>) honeycomb, (<b>b</b>) re-entrant.</p> Full article ">Figure 5
<p>Meshed lattice structures: (<b>a</b>) honeycomb explicit, (<b>b</b>) honeycomb implicit, (<b>c</b>) re-entrant explicit, (<b>d</b>) re-entrant implicit.</p> Full article ">
Open AccessArticle
Parameter Estimation of Nonlinear Structural Systems Using Bayesian Filtering Methods
by
Kalil Erazo
Vibration 2025, 8(1), 1; https://doi.org/10.3390/vibration8010001 - 31 Dec 2024
Abstract
►▼
Show Figures
This paper examines the performance of Bayesian filtering system identification in the context of nonlinear structural and mechanical systems. The objective is to assess the accuracy and limitations of the four most well-established filtering-based parameter estimation methods: the extended Kalman filter, the unscented
[...] Read more.
This paper examines the performance of Bayesian filtering system identification in the context of nonlinear structural and mechanical systems. The objective is to assess the accuracy and limitations of the four most well-established filtering-based parameter estimation methods: the extended Kalman filter, the unscented Kalman filter, the ensemble Kalman filter, and the particle filter. The four methods are applied to estimate the parameters and the response of benchmark dynamical systems used in structural mechanics, including a Duffing oscillator, a hysteretic Bouc–Wen oscillator, and a hysteretic Bouc–Wen chain system. Based on the performance, accuracy, and computational efficiency of the methods under different operating conditions, it is concluded that the unscented Kalman filter is the most effective filtering system identification method for the systems considered, with the other filters showing large estimation errors or divergence, high computational cost, and/or curse of dimensionality as the dimension of the system and the number of uncertain parameters increased.
Full article
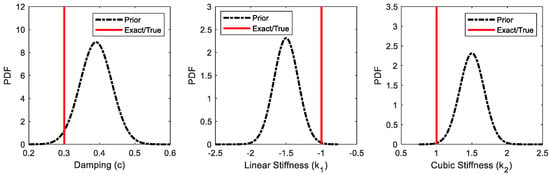
Figure 1
Figure 1
<p>Parameters prior distributions for the Duffing oscillator example (in SI units).</p> Full article ">Figure 2
<p>Damping coefficient (<math display="inline"><semantics> <mrow> <mi mathvariant="normal">c</mi> <mo>)</mo> </mrow> </semantics></math> estimates (in Ns/m).</p> Full article ">Figure 3
<p>Linear stiffness coefficient (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">k</mi> </mrow> <mrow> <mn>1</mn> </mrow> </msub> </mrow> </semantics></math>) estimates (in N/m).</p> Full article ">Figure 4
<p>Cubic stiffness coefficient (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">k</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msub> </mrow> </semantics></math>) estimates (in N/m<sup>3</sup>).</p> Full article ">Figure 5
<p>Oscillator displacement estimates (in m).</p> Full article ">Figure 6
<p>Oscillator velocity estimates (in m/s).</p> Full article ">Figure 7
<p>Parameters prior distributions for the hysteretic oscillator example (in SI units).</p> Full article ">Figure 8
<p>Hysteresis shape parameter (<math display="inline"><semantics> <mrow> <mi>β</mi> </mrow> </semantics></math>) estimates (non-dimensional).</p> Full article ">Figure 9
<p>Yielding displacement parameter (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">D</mi> </mrow> <mrow> <mi mathvariant="normal">y</mi> </mrow> </msub> </mrow> </semantics></math>) estimates (in m).</p> Full article ">Figure 10
<p>Elastic-to-Plastic transition parameter (<math display="inline"><semantics> <mrow> <mi>ν</mi> </mrow> </semantics></math>) estimates (non-dimensional).</p> Full article ">Figure 11
<p>Oscillator displacement estimates (in m).</p> Full article ">Figure 12
<p>Oscillator force–displacement hysteretic response estimates (in SI units).</p> Full article ">Figure 13
<p>Hysteretic five-degrees-of-freedom chain system.</p> Full article ">Figure 14
<p>Hysteresis parameter (<math display="inline"><semantics> <mrow> <mi>β</mi> </mrow> </semantics></math>) mean estimates for all degrees of freedom (non-dimensional).</p> Full article ">Figure 15
<p>Yielding displacement parameter (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">D</mi> </mrow> <mrow> <mi mathvariant="normal">y</mi> </mrow> </msub> </mrow> </semantics></math>) mean estimates for all degrees of freedom (in m).</p> Full article ">Figure 16
<p>Elastic-to-Plastic transition parameter (<math display="inline"><semantics> <mrow> <mi>ν</mi> </mrow> </semantics></math>) mean estimates for all degrees of freedom (non-dimensional).</p> Full article ">
<p>Parameters prior distributions for the Duffing oscillator example (in SI units).</p> Full article ">Figure 2
<p>Damping coefficient (<math display="inline"><semantics> <mrow> <mi mathvariant="normal">c</mi> <mo>)</mo> </mrow> </semantics></math> estimates (in Ns/m).</p> Full article ">Figure 3
<p>Linear stiffness coefficient (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">k</mi> </mrow> <mrow> <mn>1</mn> </mrow> </msub> </mrow> </semantics></math>) estimates (in N/m).</p> Full article ">Figure 4
<p>Cubic stiffness coefficient (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">k</mi> </mrow> <mrow> <mn>2</mn> </mrow> </msub> </mrow> </semantics></math>) estimates (in N/m<sup>3</sup>).</p> Full article ">Figure 5
<p>Oscillator displacement estimates (in m).</p> Full article ">Figure 6
<p>Oscillator velocity estimates (in m/s).</p> Full article ">Figure 7
<p>Parameters prior distributions for the hysteretic oscillator example (in SI units).</p> Full article ">Figure 8
<p>Hysteresis shape parameter (<math display="inline"><semantics> <mrow> <mi>β</mi> </mrow> </semantics></math>) estimates (non-dimensional).</p> Full article ">Figure 9
<p>Yielding displacement parameter (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">D</mi> </mrow> <mrow> <mi mathvariant="normal">y</mi> </mrow> </msub> </mrow> </semantics></math>) estimates (in m).</p> Full article ">Figure 10
<p>Elastic-to-Plastic transition parameter (<math display="inline"><semantics> <mrow> <mi>ν</mi> </mrow> </semantics></math>) estimates (non-dimensional).</p> Full article ">Figure 11
<p>Oscillator displacement estimates (in m).</p> Full article ">Figure 12
<p>Oscillator force–displacement hysteretic response estimates (in SI units).</p> Full article ">Figure 13
<p>Hysteretic five-degrees-of-freedom chain system.</p> Full article ">Figure 14
<p>Hysteresis parameter (<math display="inline"><semantics> <mrow> <mi>β</mi> </mrow> </semantics></math>) mean estimates for all degrees of freedom (non-dimensional).</p> Full article ">Figure 15
<p>Yielding displacement parameter (<math display="inline"><semantics> <mrow> <msub> <mrow> <mi mathvariant="normal">D</mi> </mrow> <mrow> <mi mathvariant="normal">y</mi> </mrow> </msub> </mrow> </semantics></math>) mean estimates for all degrees of freedom (in m).</p> Full article ">Figure 16
<p>Elastic-to-Plastic transition parameter (<math display="inline"><semantics> <mrow> <mi>ν</mi> </mrow> </semantics></math>) mean estimates for all degrees of freedom (non-dimensional).</p> Full article ">
Open AccessArticle
Mitigating Motion Sickness by Anticipatory Cues
by
Anna J. C. Reuten, Jelte E. Bos, Marieke H. Martens, Jessica Rausch and Jeroen B. J. Smeets
Vibration 2024, 7(4), 1266-1278; https://doi.org/10.3390/vibration7040065 - 21 Dec 2024
Abstract
►▼
Show Figures
Car passengers suffer much more from motion sickness compared to car drivers, presumably because drivers can better anticipate the car’s motions. Visual and auditory cues that announce upcoming motions have been demonstrated to mitigate motion sickness. In automated vehicles, vibrotactile cues might be
[...] Read more.
Car passengers suffer much more from motion sickness compared to car drivers, presumably because drivers can better anticipate the car’s motions. Visual and auditory cues that announce upcoming motions have been demonstrated to mitigate motion sickness. In automated vehicles, vibrotactile cues might be more desirable. However, prior studies provided mixed evidence regarding their effectiveness. In this study, we directly compared the effectiveness of anticipatory auditory and vibrotactile cues. We determined their effectiveness by examining self-reported motion sickness from anticipatory sessions with auditory or vibrotactile cues announcing the onset and direction of upcoming motion relative to a control session. Our preregistered analysis did not show a significant difference in mitigation between the cues but also no significant overall effect. As this lack of an effect may be due to limited statistical power, we performed an internal meta-analysis. This analysis demonstrated a small overall effect of anticipatory cues. We conclude that it is worthwhile to investigate how their effectiveness can be enhanced.
Full article

Figure 1
Figure 1
<p>Experimental apparatus. (<b>a</b>) The cabin of the linear sled offered an enclosed space that removed airflow and visual cues on motion. (<b>b</b>) Interior view of the cabin. The purple dots indicate the positions of six actuators used to present the vibrotactile cues. Replicated from Reuten et al. [<a href="#B21-vibration-07-00065" class="html-bibr">21</a>].</p> Full article ">Figure 2
<p>Presentation of the cues in relation to the motion stimulus. Bluish colors indicate the auditory sessions and reddish colors indicate the vibrotactile sessions. Filled bars represent cues indicating a forward motion; open bars represent cues indicating a backward motion. In the anticipatory sessions (<math display="inline"><semantics> <mrow> <mi>A</mi> </mrow> </semantics></math>, darker colors), the cues were presented 1 s in advance of motion onset and always indicated the initial motion direction. In the control sessions (<math display="inline"><semantics> <mrow> <mi>C</mi> </mrow> </semantics></math>, lighter colors), the cues were presented 2 to 6.5 s after motion onset and independent of the initial motion direction.</p> Full article ">Figure 3
<p>(<b>a</b>) The development of MISC scores averaged across participants for each of the four sessions. After a participant reaches the stop-criterion, they no longer contribute to the average of that session, resulting in a decrease in the average MISC. We excluded data on those time points in the anticipatory sessions when a participant reached the stop-criterion in the corresponding control session (similar to our measure <math display="inline"><semantics> <mrow> <mi>R</mi> </mrow> </semantics></math>). The inset displays the number of participants reaching the stop-criterion per time point. (<b>b</b>) The reduction values for individual participants (<math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math>) calculated for the auditory (blue) and vibrotactile (red) anticipatory sessions. The error bars are 95% confidence intervals. (<b>c</b>) The overall weighted average of the reduction (<math display="inline"><semantics> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> </semantics></math>) in motion sickness generated by each anticipatory cue. The error bars are 95% one-sided confidence intervals (coherent with our one-sided analysis). The size of the data points in panels b and c reflects the sum of MISC scores underlying the data. The horizontal lines at zero correspond to no reduction.</p> Full article ">Figure 4
<p>Results of the user experience questionnaire. Participants indicated (<b>a</b>) when they thought the cues were presented, (<b>b</b>) how often they perceived the cues, (<b>c</b>) how they evaluated the cues along a range of user dimensions (error bars indicate standard deviations), (<b>d</b>) which cue helped to mitigate motion sickness, (<b>e</b>) which cue they preferred to announce upcoming motions, and (<b>f</b>) if they would want to use the cue they preferred in their (automated) car. For the questions in panels a, d and e, the participants were given additional answer options that none of them selected.</p> Full article ">Figure 5
<p>Results of an internal meta-analysis with the reduction values calculated for each participant (<math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math>) in three comparable studies on anticipatory cueing (Kuiper et al. [<a href="#B9-vibration-07-00065" class="html-bibr">9</a>], Reuten et al. [<a href="#B21-vibration-07-00065" class="html-bibr">21</a>], and the current study). The dashed line represents the overall reduction <math display="inline"><semantics> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> </semantics></math> across all studies. Further details as in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>.</p> Full article ">Figure 6
<p>Exploratory analyses to investigate whether the between-participant variability in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>b and <a href="#vibration-07-00065-f005" class="html-fig">Figure 5</a> is characteristic of idiosyncratic benefits or the result of uncontrollable variability. (<b>a</b>) The reduction values for a sham comparison (the auditory control relative to the vibrotactile control session), for which one expects <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> = 0. The dashed line represents the overall reduction <math display="inline"><semantics> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> </semantics></math>, which is indeed close to zero. Further details as in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>b. (<b>b</b>) The <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> values for the anticipatory auditory session are plotted against those in the anticipatory vibrotactile session. In this panel, the size of the data points is determined by the square root of the product of auditory and vibrotactile <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>w</mi> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> values. The large between-participant variability in the sham comparison in Panel A and the absence of a correlation in Panel B suggest that the differences in <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> between participants in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>b and <a href="#vibration-07-00065-f005" class="html-fig">Figure 5</a> are more likely to reflect uncontrollable variability.</p> Full article ">
<p>Experimental apparatus. (<b>a</b>) The cabin of the linear sled offered an enclosed space that removed airflow and visual cues on motion. (<b>b</b>) Interior view of the cabin. The purple dots indicate the positions of six actuators used to present the vibrotactile cues. Replicated from Reuten et al. [<a href="#B21-vibration-07-00065" class="html-bibr">21</a>].</p> Full article ">Figure 2
<p>Presentation of the cues in relation to the motion stimulus. Bluish colors indicate the auditory sessions and reddish colors indicate the vibrotactile sessions. Filled bars represent cues indicating a forward motion; open bars represent cues indicating a backward motion. In the anticipatory sessions (<math display="inline"><semantics> <mrow> <mi>A</mi> </mrow> </semantics></math>, darker colors), the cues were presented 1 s in advance of motion onset and always indicated the initial motion direction. In the control sessions (<math display="inline"><semantics> <mrow> <mi>C</mi> </mrow> </semantics></math>, lighter colors), the cues were presented 2 to 6.5 s after motion onset and independent of the initial motion direction.</p> Full article ">Figure 3
<p>(<b>a</b>) The development of MISC scores averaged across participants for each of the four sessions. After a participant reaches the stop-criterion, they no longer contribute to the average of that session, resulting in a decrease in the average MISC. We excluded data on those time points in the anticipatory sessions when a participant reached the stop-criterion in the corresponding control session (similar to our measure <math display="inline"><semantics> <mrow> <mi>R</mi> </mrow> </semantics></math>). The inset displays the number of participants reaching the stop-criterion per time point. (<b>b</b>) The reduction values for individual participants (<math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math>) calculated for the auditory (blue) and vibrotactile (red) anticipatory sessions. The error bars are 95% confidence intervals. (<b>c</b>) The overall weighted average of the reduction (<math display="inline"><semantics> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> </semantics></math>) in motion sickness generated by each anticipatory cue. The error bars are 95% one-sided confidence intervals (coherent with our one-sided analysis). The size of the data points in panels b and c reflects the sum of MISC scores underlying the data. The horizontal lines at zero correspond to no reduction.</p> Full article ">Figure 4
<p>Results of the user experience questionnaire. Participants indicated (<b>a</b>) when they thought the cues were presented, (<b>b</b>) how often they perceived the cues, (<b>c</b>) how they evaluated the cues along a range of user dimensions (error bars indicate standard deviations), (<b>d</b>) which cue helped to mitigate motion sickness, (<b>e</b>) which cue they preferred to announce upcoming motions, and (<b>f</b>) if they would want to use the cue they preferred in their (automated) car. For the questions in panels a, d and e, the participants were given additional answer options that none of them selected.</p> Full article ">Figure 5
<p>Results of an internal meta-analysis with the reduction values calculated for each participant (<math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math>) in three comparable studies on anticipatory cueing (Kuiper et al. [<a href="#B9-vibration-07-00065" class="html-bibr">9</a>], Reuten et al. [<a href="#B21-vibration-07-00065" class="html-bibr">21</a>], and the current study). The dashed line represents the overall reduction <math display="inline"><semantics> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> </semantics></math> across all studies. Further details as in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>.</p> Full article ">Figure 6
<p>Exploratory analyses to investigate whether the between-participant variability in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>b and <a href="#vibration-07-00065-f005" class="html-fig">Figure 5</a> is characteristic of idiosyncratic benefits or the result of uncontrollable variability. (<b>a</b>) The reduction values for a sham comparison (the auditory control relative to the vibrotactile control session), for which one expects <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> = 0. The dashed line represents the overall reduction <math display="inline"><semantics> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> </semantics></math>, which is indeed close to zero. Further details as in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>b. (<b>b</b>) The <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> values for the anticipatory auditory session are plotted against those in the anticipatory vibrotactile session. In this panel, the size of the data points is determined by the square root of the product of auditory and vibrotactile <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>w</mi> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> values. The large between-participant variability in the sham comparison in Panel A and the absence of a correlation in Panel B suggest that the differences in <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>R</mi> </mrow> <mo>¯</mo> </mover> </mrow> <mrow> <mi>i</mi> </mrow> </msub> </mrow> </semantics></math> between participants in <a href="#vibration-07-00065-f003" class="html-fig">Figure 3</a>b and <a href="#vibration-07-00065-f005" class="html-fig">Figure 5</a> are more likely to reflect uncontrollable variability.</p> Full article ">
Open AccessArticle
Stress Distribution and Transverse Vibration of Flywheel Within Linear Elastic Range
by
Desejo Filipeson Sozinando, Kgotso Koketso Leema, Vhahangwele Colleen Sigonde, Bernard Xavier Tchomeni and Alfayo Anyika Alugongo
Vibration 2024, 7(4), 1248-1265; https://doi.org/10.3390/vibration7040064 - 13 Dec 2024
Abstract
►▼
Show Figures
Flywheels have been largely used in rotating machine engines to save inertial energy and to limit speed fluctuations. A stress distribution problem is created due to the centrifugal forces that are formed when the flywheel is spinning around, which leads to different levels
[...] Read more.
Flywheels have been largely used in rotating machine engines to save inertial energy and to limit speed fluctuations. A stress distribution problem is created due to the centrifugal forces that are formed when the flywheel is spinning around, which leads to different levels of pressure and decompression inside its structure. Lack of balance leads to high energy losses through various mechanisms, which deteriorate both the flywheel’s expectancy and their ability to rotate at high speeds. Deviation in the design of flywheels from their optimum performance can cause instability issues and even a catastrophic failure during operation. This paper aims to analytically examine the stress distribution of radial and tangential directions along the flywheel structure within a linear elastic range. The eigenvalues and eigenvectors, which are representative of free vibrational features, were extracted by applying finite element analysis (FEA). Natural frequencies and their corresponding vibrating mode shapes and mass participation factors were identified. Furthermore, Kirchhoff–Love plate theory was employed to model the transverse vibration of the system. A general solution for the radial component of the equation of flywheel motion was derived with the help of the Bessel function. The results show certain modes of vibration identified as particularly influential in specific directions. Advanced time-frequency analysis techniques, including but not limited to continuous wavelet transform (CWT) and Hilbert–Huang transform (HHT), were applied to extract transverse vibration features of the flywheel system. It was also found that using CWT, low-frequency vibrations contribute to the majority of the energy in the extracted signal spectrum, while HHT exposes the high-frequency components of vibration that may cause significant structural damage if not addressed in time.
Full article
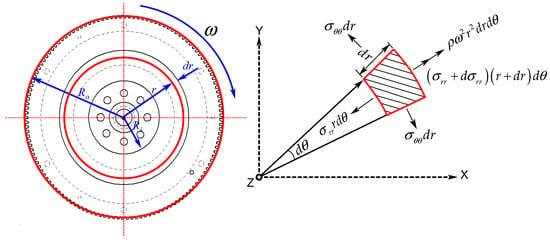
Figure 1
Figure 1
<p>Rotating flywheel and its element.</p> Full article ">Figure 2
<p>Stress distributions: (<b>a</b>) radial variation; (<b>b</b>) tangential variation.</p> Full article ">Figure 3
<p>(<b>a</b>) Variation in tangential vs. radial stresses; (<b>b</b>) displacement along flywheel radius.</p> Full article ">Figure 4
<p>Flowchart of the methodology implied in the FEA simulation.</p> Full article ">Figure 5
<p>First four deformation modes of vibration.</p> Full article ">Figure 6
<p>Waterfall response of mass participation factor.</p> Full article ">Figure 7
<p>Percentage of mass participation factor in the X, Y, and Z directions.</p> Full article ">Figure 8
<p>Four normal vibrational modes in waveform and polar spectrum of flywheel.</p> Full article ">Figure 9
<p>Transverse deflection: (<b>a</b>) time domain; (<b>b</b>) FFT response; (<b>c</b>) CWT spectrum.</p> Full article ">Figure 10
<p>Transverse velocity: (<b>a</b>) time domain; (<b>b</b>) FFT response; (<b>c</b>) CWT spectrum.</p> Full article ">Figure 11
<p>Block diagram of the IF extraction based on HHT.</p> Full article ">Figure 12
<p>Extraction of IMFs and IF based on HHT.</p> Full article ">
<p>Rotating flywheel and its element.</p> Full article ">Figure 2
<p>Stress distributions: (<b>a</b>) radial variation; (<b>b</b>) tangential variation.</p> Full article ">Figure 3
<p>(<b>a</b>) Variation in tangential vs. radial stresses; (<b>b</b>) displacement along flywheel radius.</p> Full article ">Figure 4
<p>Flowchart of the methodology implied in the FEA simulation.</p> Full article ">Figure 5
<p>First four deformation modes of vibration.</p> Full article ">Figure 6
<p>Waterfall response of mass participation factor.</p> Full article ">Figure 7
<p>Percentage of mass participation factor in the X, Y, and Z directions.</p> Full article ">Figure 8
<p>Four normal vibrational modes in waveform and polar spectrum of flywheel.</p> Full article ">Figure 9
<p>Transverse deflection: (<b>a</b>) time domain; (<b>b</b>) FFT response; (<b>c</b>) CWT spectrum.</p> Full article ">Figure 10
<p>Transverse velocity: (<b>a</b>) time domain; (<b>b</b>) FFT response; (<b>c</b>) CWT spectrum.</p> Full article ">Figure 11
<p>Block diagram of the IF extraction based on HHT.</p> Full article ">Figure 12
<p>Extraction of IMFs and IF based on HHT.</p> Full article ">
Open AccessArticle
Theoretical and Experimental Vibration Generation in a Coaxial Pulse-Tube Cryocooler
by
Hongyan Wei, Yulan Li, Yuqiang Xun and Huaqiang Zhong
Vibration 2024, 7(4), 1226-1247; https://doi.org/10.3390/vibration7040063 - 11 Dec 2024
Abstract
►▼
Show Figures
The microphonic noise induced by the vibration from cryocoolers has been found to cause energy resolution degradation in vibration-sensitive instruments. In this paper, theoretical and experimental research on the vibration generation mechanism of an aerospace-grade coaxial pulse-tube cryocooler (CPTC) is presented. Accordingly, suggestions
[...] Read more.
The microphonic noise induced by the vibration from cryocoolers has been found to cause energy resolution degradation in vibration-sensitive instruments. In this paper, theoretical and experimental research on the vibration generation mechanism of an aerospace-grade coaxial pulse-tube cryocooler (CPTC) is presented. Accordingly, suggestions for suppressing the vibration of the pulse-tube cryocooler are provided. A vibration model for the Oxford-type dual-opposed linear compressor is established, and the mechanism of vibration induced by the compressor is theoretically analyzed. A numerical simulation indicates that deviations in the compressor’s inductance coefficient, electromagnetic force coefficient, and flexure spring stiffness coefficient significantly affect the axial vibration of the compressor. The theoretical and experimental studies show that the high-order harmonic vibrations of the compressor are determined by both the resonance of the flexure springs and the high-order harmonics of the driving power supply. Through experiments and simulations, it is revealed that the dynamic gas pressure only induces vibration axially at the cold tip, while the radial vibration at the cold tip is determined by the heat head ‘s vibration and the structural response characteristics of the cold finger.
Full article
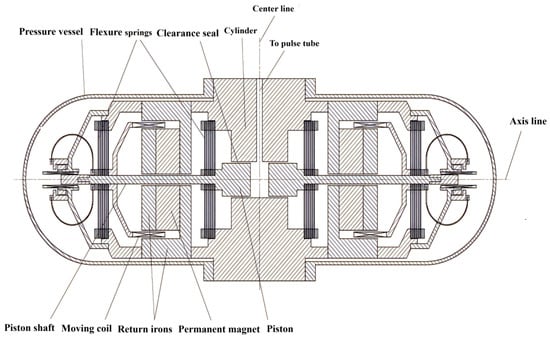
Figure 1
Figure 1
<p>Schematic of the Oxford-style dual-opposed moving-coil linear compressor.</p> Full article ">Figure 2
<p>Schematic of a single-degree-of-freedom mechanical force system in a compressor.</p> Full article ">Figure 3
<p>Equivalent circuit diagram in a compressor.</p> Full article ">Figure 4
<p>Diagram of the Simulink model for the dual-opposed compressor’s vibration analysis.</p> Full article ">Figure 5
<p>Schematic diagram of the cold finger vibration model.</p> Full article ">Figure 6
<p>Schematic diagram of gas micro cluster flow inside the cold finger.</p> Full article ">Figure 7
<p>Stress distribution diagrams of the cold finger on the transverse and longitudinal sections under radial pressure (<b>a</b>) and axial pressure (<b>b</b>).</p> Full article ">Figure 8
<p>Schematic diagram of axial strain displacement under the action of axial pressure waves (<b>a</b>) and radial pressure (<b>b</b>) at the cold tip.</p> Full article ">Figure 9
<p>Strain displacement generated by pressure waves at the cold tip.</p> Full article ">Figure 10
<p>Variation in cold tip axial vibration acceleration with pressure amplitude.</p> Full article ">Figure 11
<p>Test system of the drive power supply’s harmonic distortion.</p> Full article ">Figure 12
<p>NF (<b>a</b>) and ITM 7383 (<b>b</b>) power voltage quality.</p> Full article ">Figure 13
<p>Test system of compressor drive power distortion vs. vibration force.</p> Full article ">Figure 14
<p>Characterization of compressor operating current (<b>a</b>) and compressor vibration force (<b>b</b>) under different drive powers.</p> Full article ">Figure 15
<p>Compressor vibration force under different drive powers.</p> Full article ">Figure 16
<p>Illustration of the flexure spring configuration.</p> Full article ">Figure 17
<p>The test platform of flexure springs’ resonance impact (<b>a</b>) and laser displacement monitoring points (<b>b</b>).</p> Full article ">Figure 18
<p>Flexure springs’ axial displacement with varying frequency.</p> Full article ">Figure 19
<p>Flexure springs’ axial displacement on the left (<b>a</b>) and right (<b>b</b>) with varying frequency.</p> Full article ">Figure 20
<p>Axial vibration force spectrum of compressor during flexure spring resonance.</p> Full article ">Figure 21
<p>Flexure spring driving displacement at 108.8 Hz (resonance) (<b>a</b>) and compressor’s vibration force FFT spectrum (<b>b</b>).</p> Full article ">Figure 22
<p>Flexure spring driving displacement at 77.2 Hz (resonance) (<b>a</b>) and compressor vibration force FFT spectrum (<b>b</b>).</p> Full article ">Figure 23
<p>Flexure spring driving displacement at 136.8 Hz (resonance) (<b>a</b>) and compressor’s vibration force FFT spectrum (<b>b</b>).</p> Full article ">Figure 24
<p>System for testing the cold finger’s vibration acceleration.</p> Full article ">Figure 25
<p>FFT spectral distribution of vibration acceleration in cold finger radial (<b>a</b>), vertical (<b>b</b>) and axial (<b>c</b>) directions under a charge pressure 0 MPa.</p> Full article ">Figure 26
<p>Cold tip’s radial vibration acceleration gains factor (<b>a</b>) and FFT spectra of radial vibration acceleration at heat head 2 (<b>b</b>) and cold tip (<b>c</b>) under different charge pressures.</p> Full article ">Figure 27
<p>Cold tip’s axial vibration acceleration gain factor: (<b>a</b>) FFT spectra of axial vibration acceleration at heat head 2 (<b>b</b>) and cold tip (<b>c</b>) under different charge pressures.</p> Full article ">Figure 28
<p>Cold tip’s vertical vibration acceleration gains factor (<b>a</b>) and FFT spectra of vertical vibration acceleration at heat head 2 (<b>b</b>) and cold tip (<b>c</b>) under different charge pressures.</p> Full article ">Figure 29
<p>Axial vibration acceleration at the cold tip under different driving powers.</p> Full article ">
<p>Schematic of the Oxford-style dual-opposed moving-coil linear compressor.</p> Full article ">Figure 2
<p>Schematic of a single-degree-of-freedom mechanical force system in a compressor.</p> Full article ">Figure 3
<p>Equivalent circuit diagram in a compressor.</p> Full article ">Figure 4
<p>Diagram of the Simulink model for the dual-opposed compressor’s vibration analysis.</p> Full article ">Figure 5
<p>Schematic diagram of the cold finger vibration model.</p> Full article ">Figure 6
<p>Schematic diagram of gas micro cluster flow inside the cold finger.</p> Full article ">Figure 7
<p>Stress distribution diagrams of the cold finger on the transverse and longitudinal sections under radial pressure (<b>a</b>) and axial pressure (<b>b</b>).</p> Full article ">Figure 8
<p>Schematic diagram of axial strain displacement under the action of axial pressure waves (<b>a</b>) and radial pressure (<b>b</b>) at the cold tip.</p> Full article ">Figure 9
<p>Strain displacement generated by pressure waves at the cold tip.</p> Full article ">Figure 10
<p>Variation in cold tip axial vibration acceleration with pressure amplitude.</p> Full article ">Figure 11
<p>Test system of the drive power supply’s harmonic distortion.</p> Full article ">Figure 12
<p>NF (<b>a</b>) and ITM 7383 (<b>b</b>) power voltage quality.</p> Full article ">Figure 13
<p>Test system of compressor drive power distortion vs. vibration force.</p> Full article ">Figure 14
<p>Characterization of compressor operating current (<b>a</b>) and compressor vibration force (<b>b</b>) under different drive powers.</p> Full article ">Figure 15
<p>Compressor vibration force under different drive powers.</p> Full article ">Figure 16
<p>Illustration of the flexure spring configuration.</p> Full article ">Figure 17
<p>The test platform of flexure springs’ resonance impact (<b>a</b>) and laser displacement monitoring points (<b>b</b>).</p> Full article ">Figure 18
<p>Flexure springs’ axial displacement with varying frequency.</p> Full article ">Figure 19
<p>Flexure springs’ axial displacement on the left (<b>a</b>) and right (<b>b</b>) with varying frequency.</p> Full article ">Figure 20
<p>Axial vibration force spectrum of compressor during flexure spring resonance.</p> Full article ">Figure 21
<p>Flexure spring driving displacement at 108.8 Hz (resonance) (<b>a</b>) and compressor’s vibration force FFT spectrum (<b>b</b>).</p> Full article ">Figure 22
<p>Flexure spring driving displacement at 77.2 Hz (resonance) (<b>a</b>) and compressor vibration force FFT spectrum (<b>b</b>).</p> Full article ">Figure 23
<p>Flexure spring driving displacement at 136.8 Hz (resonance) (<b>a</b>) and compressor’s vibration force FFT spectrum (<b>b</b>).</p> Full article ">Figure 24
<p>System for testing the cold finger’s vibration acceleration.</p> Full article ">Figure 25
<p>FFT spectral distribution of vibration acceleration in cold finger radial (<b>a</b>), vertical (<b>b</b>) and axial (<b>c</b>) directions under a charge pressure 0 MPa.</p> Full article ">Figure 26
<p>Cold tip’s radial vibration acceleration gains factor (<b>a</b>) and FFT spectra of radial vibration acceleration at heat head 2 (<b>b</b>) and cold tip (<b>c</b>) under different charge pressures.</p> Full article ">Figure 27
<p>Cold tip’s axial vibration acceleration gain factor: (<b>a</b>) FFT spectra of axial vibration acceleration at heat head 2 (<b>b</b>) and cold tip (<b>c</b>) under different charge pressures.</p> Full article ">Figure 28
<p>Cold tip’s vertical vibration acceleration gains factor (<b>a</b>) and FFT spectra of vertical vibration acceleration at heat head 2 (<b>b</b>) and cold tip (<b>c</b>) under different charge pressures.</p> Full article ">Figure 29
<p>Axial vibration acceleration at the cold tip under different driving powers.</p> Full article ">
Open AccessArticle
Analysis of Displacement Transmissibility and Bifurcation Behavior in Nonlinear Systems with Friction and Nonlinear Spring
by
Deog Jae Hur and Sung Chul Hong
Vibration 2024, 7(4), 1210-1225; https://doi.org/10.3390/vibration7040062 - 3 Dec 2024
Abstract
In this paper, a nonlinear vibration system with friction and linear and nonlinear springs is modeled and analyzed. The analysis examined how the combination of nonlinear variables affects the displacement of the system using the slowly varying amplitude and phase (SVAP) method. The
[...] Read more.
In this paper, a nonlinear vibration system with friction and linear and nonlinear springs is modeled and analyzed. The analysis examined how the combination of nonlinear variables affects the displacement of the system using the slowly varying amplitude and phase (SVAP) method. The break-loose frequency at which relative motion begins was obtained as a function of the friction ratio, and it was found that the displacement transmissibility differed depending on the change in design parameters. The displacement transmissibility response showed a unique phenomenon in which bifurcation occurred in the front resonant branch before the maximum response point when the linear damping coefficient was small and the friction coefficient was large, and the displacement transfer curve was separated at a specific parameter value. This phenomenon can be divided into three parameter zones considering the bifurcation pattern and stability of the displacement transmissibility curve. In addition, a 3-D spatial zone of dimensionless parameters was presented, which can predict stability during the design process, along with the drawing method and procedure. This can be conveniently utilized in the process of setting the parameters of the isolators considering the stability of the response during the design. In the analysis and design process of vibration isolators with friction damping, this study has important implications for practical applications.
Full article
(This article belongs to the Special Issue Nonlinear Vibration of Mechanical Systems)
►▼
Show Figures
Figure 1
Figure 1
<p>Base excited nonlinear vibration system including friction damping.</p> Full article ">Figure 2
<p>Sticking and slip regions in <math display="inline"><semantics> <mrow> <mi>Ω</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane and the separating threshold line.</p> Full article ">Figure 3
<p>Absolute displacement transmissibility of linear spring system (<math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>). (<b>a</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.00 for <math display="inline"><semantics> <mrow> <mi>η</mi> </mrow> </semantics></math> = 0, 0.2, 0.4, 0.5, 1.0, (<b>b</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.03 for <math display="inline"><semantics> <mrow> <mi>η</mi> </mrow> </semantics></math> = 0, 0.2, 0.4, 0.5, 1.0.</p> Full article ">Figure 4
<p>Absolute displacement transmissibility of a nonlinear system with respect to friction and frequency ratio for a spring stiffness ratio of <span class="html-italic">μ</span> = 0.2. The dashed lines denote the unstable branch regions, and the circle markers indicate the locations of the LP bifurcations. (<b>a</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.00, (<b>b</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.04, (<b>c</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.08, (<b>d</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.2 for <span class="html-italic">η</span> = 0, 0.2, 0.4, 0.6, 1.0.</p> Full article ">Figure 5
<p>Three types of displacement transmissibility responses that occur depending on system design parameters; the dotted line is an unstable region; and the end point of the dotted line is the LP Bifurcation point. (<b>a</b>) Type I with a concave or narrow-waist shape due to the LP bifurcation points (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.02</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>b</b>) Type II separated into a host branch and a sub-branch (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.08</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>c</b>) Type III without bifurcation in front resonant branch curve (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math>).</p> Full article ">Figure 5 Cont.
<p>Three types of displacement transmissibility responses that occur depending on system design parameters; the dotted line is an unstable region; and the end point of the dotted line is the LP Bifurcation point. (<b>a</b>) Type I with a concave or narrow-waist shape due to the LP bifurcation points (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.02</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>b</b>) Type II separated into a host branch and a sub-branch (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.08</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>c</b>) Type III without bifurcation in front resonant branch curve (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math>).</p> Full article ">Figure 6
<p>Transition of TR curves and the trajectory of LP bifurcations in the <math display="inline"><semantics> <mrow> <mi>Ω</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane, with <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.02</mn> <mo>.</mo> </mrow> </semantics></math> (<b>a</b>) Transmissibility curve due to frequency ratio for η = 0.7, 0.6565, 0.6, 0.5, 0.4, 0.5, 1.0 and Limit Point, (<b>b</b>) Trajectory of Limit Points due to friction ratio at the left figure.</p> Full article ">Figure 7
<p>Trajectories of LP Bifurcations according to various damping ratios <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> for <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math> in the <math display="inline"><semantics> <mrow> <mi>Ω</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane. The dashed line means the boundary between stick and slip.</p> Full article ">Figure 8
<p>Tracking diagram of <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>C</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math>, <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>K</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math>, and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>R</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> points in <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane with <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math> and regions delineated by them. (Sky blue is zone I, white is zone II, coral is zone III).</p> Full article ">Figure 9
<p>Tracking diagram of <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>C</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>K</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> points in <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane with <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.5</mn> </mrow> </semantics></math> and regions delineated by them. (Sky blue is zone I, white is zone II, coral is zone III).</p> Full article ">Figure 10
<p>Tracking diagram of <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>C</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>K</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> points in <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>−</mo> <mi>μ</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> space and regions delineated by them. (Zone I is a volume where the sky blue colored areas are connected in the nonlinear stiffness ratio <math display="inline"><semantics> <mrow> <mi>μ</mi> </mrow> </semantics></math> direction, zone II is a volume where the white-colored areas are connected, and zone III is a volume where the coral-colored areas are connected).</p> Full article ">
<p>Base excited nonlinear vibration system including friction damping.</p> Full article ">Figure 2
<p>Sticking and slip regions in <math display="inline"><semantics> <mrow> <mi>Ω</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane and the separating threshold line.</p> Full article ">Figure 3
<p>Absolute displacement transmissibility of linear spring system (<math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0</mn> </mrow> </semantics></math>). (<b>a</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.00 for <math display="inline"><semantics> <mrow> <mi>η</mi> </mrow> </semantics></math> = 0, 0.2, 0.4, 0.5, 1.0, (<b>b</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.03 for <math display="inline"><semantics> <mrow> <mi>η</mi> </mrow> </semantics></math> = 0, 0.2, 0.4, 0.5, 1.0.</p> Full article ">Figure 4
<p>Absolute displacement transmissibility of a nonlinear system with respect to friction and frequency ratio for a spring stiffness ratio of <span class="html-italic">μ</span> = 0.2. The dashed lines denote the unstable branch regions, and the circle markers indicate the locations of the LP bifurcations. (<b>a</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.00, (<b>b</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.04, (<b>c</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.08, (<b>d</b>) Transmissibility curve due to frequency ratio at <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> = 0.2 for <span class="html-italic">η</span> = 0, 0.2, 0.4, 0.6, 1.0.</p> Full article ">Figure 5
<p>Three types of displacement transmissibility responses that occur depending on system design parameters; the dotted line is an unstable region; and the end point of the dotted line is the LP Bifurcation point. (<b>a</b>) Type I with a concave or narrow-waist shape due to the LP bifurcation points (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.02</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>b</b>) Type II separated into a host branch and a sub-branch (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.08</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>c</b>) Type III without bifurcation in front resonant branch curve (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math>).</p> Full article ">Figure 5 Cont.
<p>Three types of displacement transmissibility responses that occur depending on system design parameters; the dotted line is an unstable region; and the end point of the dotted line is the LP Bifurcation point. (<b>a</b>) Type I with a concave or narrow-waist shape due to the LP bifurcation points (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.02</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>b</b>) Type II separated into a host branch and a sub-branch (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.08</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.6</mn> </mrow> </semantics></math>), (<b>c</b>) Type III without bifurcation in front resonant branch curve (<math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> <mo>,</mo> <mo> </mo> <mi>η</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math>).</p> Full article ">Figure 6
<p>Transition of TR curves and the trajectory of LP bifurcations in the <math display="inline"><semantics> <mrow> <mi>Ω</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane, with <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>=</mo> <mn>0.02</mn> <mo>.</mo> </mrow> </semantics></math> (<b>a</b>) Transmissibility curve due to frequency ratio for η = 0.7, 0.6565, 0.6, 0.5, 0.4, 0.5, 1.0 and Limit Point, (<b>b</b>) Trajectory of Limit Points due to friction ratio at the left figure.</p> Full article ">Figure 7
<p>Trajectories of LP Bifurcations according to various damping ratios <math display="inline"><semantics> <mrow> <mi>ζ</mi> </mrow> </semantics></math> for <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math> in the <math display="inline"><semantics> <mrow> <mi>Ω</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane. The dashed line means the boundary between stick and slip.</p> Full article ">Figure 8
<p>Tracking diagram of <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>C</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math>, <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>K</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math>, and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>R</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> points in <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane with <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.2</mn> </mrow> </semantics></math> and regions delineated by them. (Sky blue is zone I, white is zone II, coral is zone III).</p> Full article ">Figure 9
<p>Tracking diagram of <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>C</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>K</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> points in <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> plane with <math display="inline"><semantics> <mrow> <mi>μ</mi> <mo>=</mo> <mn>0.5</mn> </mrow> </semantics></math> and regions delineated by them. (Sky blue is zone I, white is zone II, coral is zone III).</p> Full article ">Figure 10
<p>Tracking diagram of <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>C</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> and <math display="inline"><semantics> <mrow> <msub> <mrow> <mi>K</mi> </mrow> <mrow> <mi>p</mi> </mrow> </msub> </mrow> </semantics></math> points in <math display="inline"><semantics> <mrow> <mi>ζ</mi> <mo>−</mo> <mi>μ</mi> <mo>−</mo> <mi>η</mi> </mrow> </semantics></math> space and regions delineated by them. (Zone I is a volume where the sky blue colored areas are connected in the nonlinear stiffness ratio <math display="inline"><semantics> <mrow> <mi>μ</mi> </mrow> </semantics></math> direction, zone II is a volume where the white-colored areas are connected, and zone III is a volume where the coral-colored areas are connected).</p> Full article ">
Open AccessArticle
Research on the Seismic Response of Hybrid Concrete/Steel Structures Equipped with the Seesaw System
by
George A. Papagiannopoulos, Panagiota S. Katsimpini and George D. Hatzigeorgiou
Vibration 2024, 7(4), 1190-1209; https://doi.org/10.3390/vibration7040061 - 1 Dec 2024
Abstract
►▼
Show Figures
This research investigates the seismic performance of structures equipped with the seesaw system in relation to conventional structures within two- and five-storey mixed concrete and steel buildings. Through time history analysis, the study assesses structural responses to severe ground motion accelerograms, taking into
[...] Read more.
This research investigates the seismic performance of structures equipped with the seesaw system in relation to conventional structures within two- and five-storey mixed concrete and steel buildings. Through time history analysis, the study assesses structural responses to severe ground motion accelerograms, taking into account both fixed-base conditions and soil–structure interaction (SSI) scenarios. The focus is on essential performance indicators such as maximum and residual displacements, inter-storey drift ratios, and floor accelerations. By comparing the structures with the seesaw system with bare structures, the research seeks to quantify the benefits of this novel design in mitigating seismic effects. A significant component of this study is the examination of various seismic incidence angles, specifically 0°, 90°, 180°, and 270°. This extensive approach facilitates a comprehensive evaluation of structural behavior under diverse directional loadings, thereby capturing a wide range of potential seismic responses. The analysis of these different incidence angles is vital for understanding how the orientation of structural elements, particularly steel columns in the mixed system, affects the seismic performance of the building. Additionally, incorporating SSI effects yields a more precise depiction of structural behavior during earthquakes, considering the impact of soil flexibility on the overall system response.
Full article
Figure 1
Figure 1
<p>Hybrid structure equipped with the seesaw system.</p> Full article ">Figure 2
<p>Two-storey structure with the seesaw system.</p> Full article ">Figure 3
<p>Five-storey structure with the seesaw system.</p> Full article ">Figure 4
<p>Connection between steel and concrete columns.</p> Full article ">Figure 5
<p>Two-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 6
<p>Five-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 7
<p>Modelling of SSI with rigid elements.</p> Full article ">Figure 8
<p>Plastic hinges two-storey structure with the seesaw system.</p> Full article ">Figure 9
<p>Plastic hinges two-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 10
<p>IDR (%) for two-storey structure.</p> Full article ">Figure 11
<p>Base shear (kN) for two-storey structure.</p> Full article ">Figure 12
<p>Acceleration (g) for two-storey structure.</p> Full article ">Figure 13
<p>RIDR (%) for two-storey structure.</p> Full article ">Figure 14
<p>Cable and damper forces for two-storey structure.</p> Full article ">Figure 15
<p>Plastic hinges five-storey structure with the seesaw system.</p> Full article ">Figure 16
<p>Plastic hinges five-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 17
<p>IDR (%) for five-storey structure.</p> Full article ">Figure 18
<p>Base shear (kN) for five-storey structure.</p> Full article ">Figure 19
<p>Acceleration (g) for five-storey structure.</p> Full article ">Figure 20
<p>RIDR (%) for five-storey structure.</p> Full article ">Figure 21
<p>Cable and damper forces for five-storey structure.</p> Full article ">Figure 22
<p>Variation of top horizontal displacement of the two storey structure for different angles of incidence.</p> Full article ">Figure 23
<p>Variation of top horizontal displacement of the five-storey structure for different angles of incidence.</p> Full article ">
<p>Hybrid structure equipped with the seesaw system.</p> Full article ">Figure 2
<p>Two-storey structure with the seesaw system.</p> Full article ">Figure 3
<p>Five-storey structure with the seesaw system.</p> Full article ">Figure 4
<p>Connection between steel and concrete columns.</p> Full article ">Figure 5
<p>Two-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 6
<p>Five-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 7
<p>Modelling of SSI with rigid elements.</p> Full article ">Figure 8
<p>Plastic hinges two-storey structure with the seesaw system.</p> Full article ">Figure 9
<p>Plastic hinges two-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 10
<p>IDR (%) for two-storey structure.</p> Full article ">Figure 11
<p>Base shear (kN) for two-storey structure.</p> Full article ">Figure 12
<p>Acceleration (g) for two-storey structure.</p> Full article ">Figure 13
<p>RIDR (%) for two-storey structure.</p> Full article ">Figure 14
<p>Cable and damper forces for two-storey structure.</p> Full article ">Figure 15
<p>Plastic hinges five-storey structure with the seesaw system.</p> Full article ">Figure 16
<p>Plastic hinges five-storey structure with the seesaw system considering SSI effects.</p> Full article ">Figure 17
<p>IDR (%) for five-storey structure.</p> Full article ">Figure 18
<p>Base shear (kN) for five-storey structure.</p> Full article ">Figure 19
<p>Acceleration (g) for five-storey structure.</p> Full article ">Figure 20
<p>RIDR (%) for five-storey structure.</p> Full article ">Figure 21
<p>Cable and damper forces for five-storey structure.</p> Full article ">Figure 22
<p>Variation of top horizontal displacement of the two storey structure for different angles of incidence.</p> Full article ">Figure 23
<p>Variation of top horizontal displacement of the five-storey structure for different angles of incidence.</p> Full article ">
Open AccessArticle
Stirred Not Shaken: A Longitudinal Pilot Study of Head Kinematics and Cognitive Changes in Horseracing
by
Emma Edwards, Bert Bond, Timothy P. Holsgrove, Jerry Hill, Ryan Baker and Genevieve K. R. Williams
Vibration 2024, 7(4), 1171-1189; https://doi.org/10.3390/vibration7040060 - 27 Nov 2024
Abstract
The purpose of this longitudinal pilot study was to add to the body of research relating to head kinematics/vibration in sport and their potential to cause short-term alterations in brain function. In horseracing, due to the horse’s movement, repeated low-level accelerations are transmitted
[...] Read more.
The purpose of this longitudinal pilot study was to add to the body of research relating to head kinematics/vibration in sport and their potential to cause short-term alterations in brain function. In horseracing, due to the horse’s movement, repeated low-level accelerations are transmitted to the jockey’s head. To measure this, professional jockeys (2 male, 2 female) wore an inertial measurement unit (IMU) to record their head kinematics while riding out. In addition, a short battery of tests (Stroop, Trail Making Test B, choice reaction time, manual dexterity, and visual function) was completed immediately before and after riding. Pre- and post-outcome measures from the cognitive test battery were compared using descriptive statistics. The average head kinematics measured across all jockeys and days were at a low level: resultant linear acceleration peak = 5.82 ± 1.08 g, mean = 1.02 ± 0.01 g; resultant rotational velocity peak = 10.37 ± 3.23 rad/s, mean = 0.85 ± 0.15 rad/s; and resultant rotational acceleration peak = 1495 ± 532.75 rad/s2, mean = 86.58 ± 15.54 rad/s2. The duration of an acceleration event was on average 127.04 ± 17.22 ms for linear accelerations and 89.42 ± 19.74 ms for rotational accelerations. This was longer than those noted in many impact and non-impact sports. Jockeys experienced high counts of linear and rotational head accelerations above 3 g and 400 rad/s2, which are considered normal daily living levels (average 300 linear and 445 rotational accelerations per hour of riding). No measurable decline in executive function or dexterity was found after riding; however, a deterioration in visual function (near point convergence and accommodation) was seen. This work lays the foundation for future large-scale research to monitor the head kinematics of riders, measure the effects and understand variables that might influence them.
Full article
(This article belongs to the Special Issue Vibrations in Sports)
►▼
Show Figures
Figure 1
Figure 1
<p>Schematic of the typical workload in a year and a typical week during the season for a UK professional flat jockey.</p> Full article ">Figure 2
<p>Position of the inertial measurement unit attached on the mastoid process behind a jockey’s right ear.</p> Full article ">Figure 3
<p>Heat maps of average daily exposure to head accelerations at the three time points, yellow asterisks (*) mark the peak values measured on those days. (<b>a</b>) Linear head acceleration counts above 3 g where the x-axis is the acceleration in g and the y-axis is each day of the data collection; (<b>b</b>) Rotational head acceleration counts above 400 rad/s, where the x-axis is rotational acceleration in rad/s<sup>2</sup> and the y-axis is each day of the data collection.</p> Full article ">
<p>Schematic of the typical workload in a year and a typical week during the season for a UK professional flat jockey.</p> Full article ">Figure 2
<p>Position of the inertial measurement unit attached on the mastoid process behind a jockey’s right ear.</p> Full article ">Figure 3
<p>Heat maps of average daily exposure to head accelerations at the three time points, yellow asterisks (*) mark the peak values measured on those days. (<b>a</b>) Linear head acceleration counts above 3 g where the x-axis is the acceleration in g and the y-axis is each day of the data collection; (<b>b</b>) Rotational head acceleration counts above 400 rad/s, where the x-axis is rotational acceleration in rad/s<sup>2</sup> and the y-axis is each day of the data collection.</p> Full article ">
Open AccessArticle
Non-Linear Dynamic Analysis of Timber Frame Structure with Bolted-Fastener Connections
by
Thomas Catterou, Yann Sousseau, Sidi Mohammed Elachachi, Myriam Chaplain and Carole Faye
Vibration 2024, 7(4), 1156-1170; https://doi.org/10.3390/vibration7040059 - 26 Nov 2024
Abstract
►▼
Show Figures
Understanding the dynamics of timber structures is essential for the timber structural engineering field, where it is necessary to build predictive numerical models and digital twins. Three similar-sized representative post-beam bracing frames with wood–metal assemblies were tested. Experimental modal analysis gave some indication
[...] Read more.
Understanding the dynamics of timber structures is essential for the timber structural engineering field, where it is necessary to build predictive numerical models and digital twins. Three similar-sized representative post-beam bracing frames with wood–metal assemblies were tested. Experimental modal analysis gave some indication of the non-linear behaviour of the structure. Then, the frame was submitted to a logarithmic sine sweep, which highlighted some specificities of the non-linear modes: dependence on the sweep direction and amplitude, jump, etc. These phenomena can be explained by friction and shocks in the assemblies. An accurate model of these non-linearities could lead to resilient and more earthquake-resistant timber structures, as the equivalent damping of a non-linear structure is way lower than for a linear one.
Full article

Figure 1
Figure 1
<p>(<b>a</b>) Testing bracing frame structure; (<b>b</b>) wood–metal joints.</p> Full article ">Figure 2
<p>Test configuration.</p> Full article ">Figure 3
<p>Locations of sensors and hammer hits.</p> Full article ">Figure 4
<p>Mode shapes of the experimental first flexural mode (<b>left</b>) and numerical first flexural mode (<b>right</b>).</p> Full article ">Figure 5
<p>Transfer function of the structure subjected to white noise on the frequency range [0, 20 Hz].</p> Full article ">Figure 6
<p>Stability diagram of the experimental modal analysis conducted on the first frame.</p> Full article ">Figure 7
<p>Transfer function <math display="inline"><semantics> <msub> <mi>H</mi> <mrow> <mi>i</mi> <mo>,</mo> <mi>j</mi> </mrow> </msub> </semantics></math> of the impact response of the structure for hammer impacts at points 1 (<b>a</b>) and 3 (<b>b</b>). The letter <span class="html-italic">i</span> corresponds to the impact points and <span class="html-italic">j</span> to the measurement points, as defined in <a href="#vibration-07-00059-f003" class="html-fig">Figure 3</a>.</p> Full article ">Figure 8
<p>Examples of the time evolution of the acceleration for the first frame with table displacement amplitudes of ±0.5 cm (<b>left</b>) and ±2.5 cm (<b>right</b>). Red: shaking table acceleration. Blue: top structure acceleration—sweep down. Green: top structure acceleration—sweep up. The time is expressed according to the frequency of the input signal during the sweep up and the sweep down.</p> Full article ">Figure 9
<p>Frequency response functions of the three frames for three input signal amplitudes. The magnitude of the FRF corresponds to the transmissibility, the ratio between the acceleration at the top of the structure, and the acceleration of the input signal.</p> Full article ">Figure 10
<p>Time–frequency plots of the acceleration at the top of the structure of the frame 3 and for an input amplitude of ±2.5 cm. The colours correspond to the difference in dB of the signal compared with the maximum value of the signal.</p> Full article ">Figure 11
<p>Time–frequency plots of the acceleration at the top of the structure of the three frames for different load magnitudes. The colours correspond to the difference in dB of the signal compared with the maximum value of the signal.</p> Full article ">Figure 12
<p>Input displacement and structure displacement at the beginning of the sub-harmonic resonance.</p> Full article ">Figure A1
<p>Simplified technical drawing of the braced frame.</p> Full article ">Figure A2
<p>Simplified technical drawing of the assemblies.</p> Full article ">
<p>(<b>a</b>) Testing bracing frame structure; (<b>b</b>) wood–metal joints.</p> Full article ">Figure 2
<p>Test configuration.</p> Full article ">Figure 3
<p>Locations of sensors and hammer hits.</p> Full article ">Figure 4
<p>Mode shapes of the experimental first flexural mode (<b>left</b>) and numerical first flexural mode (<b>right</b>).</p> Full article ">Figure 5
<p>Transfer function of the structure subjected to white noise on the frequency range [0, 20 Hz].</p> Full article ">Figure 6
<p>Stability diagram of the experimental modal analysis conducted on the first frame.</p> Full article ">Figure 7
<p>Transfer function <math display="inline"><semantics> <msub> <mi>H</mi> <mrow> <mi>i</mi> <mo>,</mo> <mi>j</mi> </mrow> </msub> </semantics></math> of the impact response of the structure for hammer impacts at points 1 (<b>a</b>) and 3 (<b>b</b>). The letter <span class="html-italic">i</span> corresponds to the impact points and <span class="html-italic">j</span> to the measurement points, as defined in <a href="#vibration-07-00059-f003" class="html-fig">Figure 3</a>.</p> Full article ">Figure 8
<p>Examples of the time evolution of the acceleration for the first frame with table displacement amplitudes of ±0.5 cm (<b>left</b>) and ±2.5 cm (<b>right</b>). Red: shaking table acceleration. Blue: top structure acceleration—sweep down. Green: top structure acceleration—sweep up. The time is expressed according to the frequency of the input signal during the sweep up and the sweep down.</p> Full article ">Figure 9
<p>Frequency response functions of the three frames for three input signal amplitudes. The magnitude of the FRF corresponds to the transmissibility, the ratio between the acceleration at the top of the structure, and the acceleration of the input signal.</p> Full article ">Figure 10
<p>Time–frequency plots of the acceleration at the top of the structure of the frame 3 and for an input amplitude of ±2.5 cm. The colours correspond to the difference in dB of the signal compared with the maximum value of the signal.</p> Full article ">Figure 11
<p>Time–frequency plots of the acceleration at the top of the structure of the three frames for different load magnitudes. The colours correspond to the difference in dB of the signal compared with the maximum value of the signal.</p> Full article ">Figure 12
<p>Input displacement and structure displacement at the beginning of the sub-harmonic resonance.</p> Full article ">Figure A1
<p>Simplified technical drawing of the braced frame.</p> Full article ">Figure A2
<p>Simplified technical drawing of the assemblies.</p> Full article ">
Open AccessArticle
Novel Nonlinear Suspension Based on Concept of Origami Metastructures: Theoretical and Experimental Investigations
by
Antonio Zippo, Giovanni Iarriccio, Moslem Molaie and Francesco Pellicano
Vibration 2024, 7(4), 1126-1155; https://doi.org/10.3390/vibration7040058 - 22 Nov 2024
Abstract
►▼
Show Figures
This study presents a comprehensive investigation of an innovative mechanical system inspired by recent advancements in metamaterials; more specifically, the work is focused on origami-type structures due to their intriguing mechanical properties. Originating from specific fields such as aerospace for their lightweight and
[...] Read more.
This study presents a comprehensive investigation of an innovative mechanical system inspired by recent advancements in metamaterials; more specifically, the work is focused on origami-type structures due to their intriguing mechanical properties. Originating from specific fields such as aerospace for their lightweight and foldable characteristics, origami mechanical devices exhibit unique nonlinear stiffness; in particular, when suitably designed, they show Quasi-Zero Stiffness (QZS) characteristics within a specific working range. The QZS property, aligned with the High Static Low Dynamic (HSLD) stiffness concept, suggests promising applications such as a low-frequency mechanical passive vibration isolator. The study explores the vibration isolation characteristics of origami-type suspensions, with a particular emphasis on their potential application as low-frequency passive vibration isolators. The Kresling Origami Module (KOM) has been selected for its compactness and compatibility with 3D printers. A detailed analysis using 3D CAD, Finite Element Analysis, and experimental testing has been carried out. The investigation includes the analysis of the influence of geometric parameters on the nonlinear force–displacement curve. Multibody simulations validate the low-frequency isolation properties within the QZS region, as well as disparities in dynamic properties beyond the QZS range. The study underscores the transformative potential of origami-type metamaterials in enhancing low-frequency vibration isolation technology. It also highlights challenges related to material properties and loading mass variations, providing valuable insights for future developments in this promising field.
Full article
Figure 1
Figure 1
<p>QZS force–displacement behavior (black curve). Start of QZS behaviour (dotted blue line). End of QZS behaviour (dotted red line).</p> Full article ">Figure 2
<p>Kresling unit cell.</p> Full article ">Figure 3
<p>Representing the geometry of all five cases. (<b>a</b>) KOM-0, (<b>b</b>) KOM-I, (<b>c</b>) KOM-II, (<b>d</b>) KOM-III, (<b>e</b>) KOM-IV.</p> Full article ">Figure 3 Cont.
<p>Representing the geometry of all five cases. (<b>a</b>) KOM-0, (<b>b</b>) KOM-I, (<b>c</b>) KOM-II, (<b>d</b>) KOM-III, (<b>e</b>) KOM-IV.</p> Full article ">Figure 4
<p>Elements for meshing the geometries.</p> Full article ">Figure 5
<p>Element selection for FEA; <span style="color:red">▬</span> shell element; <span style="color:blue">▬</span> solid element.</p> Full article ">Figure 6
<p>Comparing all eight cases in terms of the following: (<b>a</b>) Force–Displacement; (<b>b</b>) Stiffness–Displacement <span style="color:blue">▬</span> KOM-I; <span style="color:blue">▬</span> <span style="color:blue">●</span> <span style="color:blue">▬</span> KOM-Ia; <span style="color:red">▬</span> KOM-II; <span style="color:red">▬</span> <span style="color:red">●</span> <span style="color:red">▬</span> KOM-IIa; ▬ KOM-III; ▬ ● ▬ KOM-IIIa; <span style="color:#00B050">▬</span> KOM-IV; <span style="color:#00B050">▬</span> <span style="color:#00B050">●</span> <span style="color:#00B050">▬</span> KOM-Iva.</p> Full article ">Figure 7
<p>Strain analysis simulation parameters.</p> Full article ">Figure 8
<p>A scheme of the middle plane shift angle.</p> Full article ">Figure 9
<p>Evaluating the effect of the angular shift: <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>20</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>30</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>40</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>50</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>.</p> Full article ">Figure 10
<p>A scheme where the distance between middle and base planes is illustrated.</p> Full article ">Figure 11
<p>Evaluating the effect of middle plane height. (<b>a</b>) Force–Displacement, (<b>b</b>) Stiffness–Displacement: <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>10</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>14</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>18</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>22</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>26</mn> <mo> </mo> <mi>mm</mi> <mo>.</mo> </mrow> </semantics></math>.</p> Full article ">Figure 12
<p>A scheme of the base length.</p> Full article ">Figure 13
<p>Evaluating the effect of base length, <math display="inline"><semantics> <mi>l</mi> </semantics></math>; (<b>a</b>) Force–Displacement, (<b>b</b>) Stiffness–Displacement: <span style="color:#00FFFF">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>6</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>10</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>14</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>18</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>22</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>26</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>.</p> Full article ">Figure 14
<p>Evaluating the effect of base length, <math display="inline"><semantics> <mi>t</mi> </semantics></math>; <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.2</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.3</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.4</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.5</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.6</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 15
<p>KOM multibody model.</p> Full article ">Figure 16
<p>FEA for KOM-IIb in the compression stroke: (<b>a</b>) Force–displacement; (<b>b</b>) Stiffness-displacement diagram.</p> Full article ">Figure 17
<p>Working regions for the compression stroke.</p> Full article ">Figure 18
<p>Magnitude and Phase FRF comparison.</p> Full article ">Figure 19
<p>The KOM-III models under compressive load (numerical results) <span style="color:#00FFFF">▬</span> KOM-III.1; <span style="color:blue">▬</span> KOM-III.2; <span style="color:red">▬</span> KOM-III.3; ▬ KOM-III.4; <span style="color:#00B050">▬</span> KOM-III.5; <span style="color:#FF00FF">▬</span> KOM-III.6; <span style="color:#FF9900">▬</span> KOM-III.7; <span style="color:#990000">▬</span> KOM-III.8.</p> Full article ">Figure 20
<p>KOM under compressive load for the three different materials by means of FEA. (<b>a</b>) materials nominal mechanical properties [<a href="#B30-vibration-07-00058" class="html-bibr">30</a>]. (<b>b</b>) Force-Displacement. (<b>c</b>) Stiffness-Displacement.</p> Full article ">Figure 21
<p>KOM-III.3 prototype.</p> Full article ">Figure 22
<p>Compressive test setup.</p> Full article ">Figure 23
<p>Experimental results: (<b>a</b>) Force–displacement; (<b>b</b>) Average Force; (<b>c</b>) Stiffness–Displacement <span style="color:#00FFFF">▬</span> try-1; <span style="color:blue">▬</span> try-2; <span style="color:red">▬</span> try-3; <span style="color:#990000">▬</span> try-4; <span style="color:#00B050">▬</span> try-5; <span style="color:#FF00FF">▬</span> try-6.</p> Full article ">Figure 24
<p>Simulation results Force—Displacement at different E values <span style="color:#FF9900">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>1</mn> </msub> <mo>=</mo> <mn>7</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:#990000">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>2</mn> </msub> <mo>=</mo> <mn>8</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>3</mn> </msub> <mo>=</mo> <mn>9</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>4</mn> </msub> <mo>=</mo> <mn>10</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>5</mn> </msub> <mo>=</mo> <mn>11</mn> <mo> </mo> <mi>Pa</mi> </mrow> </semantics></math>; <span style="color:#00FFFF">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>6</mn> </msub> <mo>=</mo> <mn>12</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>7</mn> </msub> <mo>=</mo> <mn>14</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; ▬ Exp. Data.</p> Full article ">Figure 25
<p>Comparison between the following: (<b>a</b>) Force–displacement; (<b>b</b>) Stiffness–displacement characteristics: <span style="color:red">▬</span> Experimental results; ▬ FEA results.</p> Full article ">Figure 26
<p>FRF comparison between multibody model based on FEM and experimental stiffness.</p> Full article ">
<p>QZS force–displacement behavior (black curve). Start of QZS behaviour (dotted blue line). End of QZS behaviour (dotted red line).</p> Full article ">Figure 2
<p>Kresling unit cell.</p> Full article ">Figure 3
<p>Representing the geometry of all five cases. (<b>a</b>) KOM-0, (<b>b</b>) KOM-I, (<b>c</b>) KOM-II, (<b>d</b>) KOM-III, (<b>e</b>) KOM-IV.</p> Full article ">Figure 3 Cont.
<p>Representing the geometry of all five cases. (<b>a</b>) KOM-0, (<b>b</b>) KOM-I, (<b>c</b>) KOM-II, (<b>d</b>) KOM-III, (<b>e</b>) KOM-IV.</p> Full article ">Figure 4
<p>Elements for meshing the geometries.</p> Full article ">Figure 5
<p>Element selection for FEA; <span style="color:red">▬</span> shell element; <span style="color:blue">▬</span> solid element.</p> Full article ">Figure 6
<p>Comparing all eight cases in terms of the following: (<b>a</b>) Force–Displacement; (<b>b</b>) Stiffness–Displacement <span style="color:blue">▬</span> KOM-I; <span style="color:blue">▬</span> <span style="color:blue">●</span> <span style="color:blue">▬</span> KOM-Ia; <span style="color:red">▬</span> KOM-II; <span style="color:red">▬</span> <span style="color:red">●</span> <span style="color:red">▬</span> KOM-IIa; ▬ KOM-III; ▬ ● ▬ KOM-IIIa; <span style="color:#00B050">▬</span> KOM-IV; <span style="color:#00B050">▬</span> <span style="color:#00B050">●</span> <span style="color:#00B050">▬</span> KOM-Iva.</p> Full article ">Figure 7
<p>Strain analysis simulation parameters.</p> Full article ">Figure 8
<p>A scheme of the middle plane shift angle.</p> Full article ">Figure 9
<p>Evaluating the effect of the angular shift: <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>20</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>30</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>40</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>θ</mi> <mo>=</mo> <msup> <mrow> <mn>50</mn> </mrow> <mi mathvariant="normal">o</mi> </msup> </mrow> </semantics></math>.</p> Full article ">Figure 10
<p>A scheme where the distance between middle and base planes is illustrated.</p> Full article ">Figure 11
<p>Evaluating the effect of middle plane height. (<b>a</b>) Force–Displacement, (<b>b</b>) Stiffness–Displacement: <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>10</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>14</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>18</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>22</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <mi>h</mi> <mo>=</mo> <mn>26</mn> <mo> </mo> <mi>mm</mi> <mo>.</mo> </mrow> </semantics></math>.</p> Full article ">Figure 12
<p>A scheme of the base length.</p> Full article ">Figure 13
<p>Evaluating the effect of base length, <math display="inline"><semantics> <mi>l</mi> </semantics></math>; (<b>a</b>) Force–Displacement, (<b>b</b>) Stiffness–Displacement: <span style="color:#00FFFF">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>6</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>10</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>14</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>18</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>22</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <mi>l</mi> <mo>=</mo> <mn>26</mn> <mo> </mo> <mi>mm</mi> </mrow> </semantics></math>.</p> Full article ">Figure 14
<p>Evaluating the effect of base length, <math display="inline"><semantics> <mi>t</mi> </semantics></math>; <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.2</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.3</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; ▬ <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.4</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.5</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <mi>t</mi> <mo>=</mo> <mn>0.6</mn> <mrow> <mo> </mo> <mi>mm</mi> </mrow> </mrow> </semantics></math>.</p> Full article ">Figure 15
<p>KOM multibody model.</p> Full article ">Figure 16
<p>FEA for KOM-IIb in the compression stroke: (<b>a</b>) Force–displacement; (<b>b</b>) Stiffness-displacement diagram.</p> Full article ">Figure 17
<p>Working regions for the compression stroke.</p> Full article ">Figure 18
<p>Magnitude and Phase FRF comparison.</p> Full article ">Figure 19
<p>The KOM-III models under compressive load (numerical results) <span style="color:#00FFFF">▬</span> KOM-III.1; <span style="color:blue">▬</span> KOM-III.2; <span style="color:red">▬</span> KOM-III.3; ▬ KOM-III.4; <span style="color:#00B050">▬</span> KOM-III.5; <span style="color:#FF00FF">▬</span> KOM-III.6; <span style="color:#FF9900">▬</span> KOM-III.7; <span style="color:#990000">▬</span> KOM-III.8.</p> Full article ">Figure 20
<p>KOM under compressive load for the three different materials by means of FEA. (<b>a</b>) materials nominal mechanical properties [<a href="#B30-vibration-07-00058" class="html-bibr">30</a>]. (<b>b</b>) Force-Displacement. (<b>c</b>) Stiffness-Displacement.</p> Full article ">Figure 21
<p>KOM-III.3 prototype.</p> Full article ">Figure 22
<p>Compressive test setup.</p> Full article ">Figure 23
<p>Experimental results: (<b>a</b>) Force–displacement; (<b>b</b>) Average Force; (<b>c</b>) Stiffness–Displacement <span style="color:#00FFFF">▬</span> try-1; <span style="color:blue">▬</span> try-2; <span style="color:red">▬</span> try-3; <span style="color:#990000">▬</span> try-4; <span style="color:#00B050">▬</span> try-5; <span style="color:#FF00FF">▬</span> try-6.</p> Full article ">Figure 24
<p>Simulation results Force—Displacement at different E values <span style="color:#FF9900">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>1</mn> </msub> <mo>=</mo> <mn>7</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:#990000">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>2</mn> </msub> <mo>=</mo> <mn>8</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:#FF00FF">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>3</mn> </msub> <mo>=</mo> <mn>9</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:blue">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>4</mn> </msub> <mo>=</mo> <mn>10</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:red">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>5</mn> </msub> <mo>=</mo> <mn>11</mn> <mo> </mo> <mi>Pa</mi> </mrow> </semantics></math>; <span style="color:#00FFFF">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>6</mn> </msub> <mo>=</mo> <mn>12</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; <span style="color:#00B050">▬</span> <math display="inline"><semantics> <mrow> <msub> <mi>E</mi> <mn>7</mn> </msub> <mo>=</mo> <mn>14</mn> <mo> </mo> <mi>MPa</mi> </mrow> </semantics></math>; ▬ Exp. Data.</p> Full article ">Figure 25
<p>Comparison between the following: (<b>a</b>) Force–displacement; (<b>b</b>) Stiffness–displacement characteristics: <span style="color:red">▬</span> Experimental results; ▬ FEA results.</p> Full article ">Figure 26
<p>FRF comparison between multibody model based on FEM and experimental stiffness.</p> Full article ">
Open AccessArticle
Vibration-Based Diagnostics of Non-Ceramic Insulators: Characterization of Signals
by
Dániel Balogh, Richárd Cselkó and Gergely Márk Csányi
Vibration 2024, 7(4), 1111-1125; https://doi.org/10.3390/vibration7040057 - 18 Nov 2024
Abstract
►▼
Show Figures
This paper presents an experimental method for testing composite insulators based on vibration testing. The method used investigated the propagation, signal shape, and distortion of excited mechanical waves under the influence of defects. The aim of the method was to identify defects in
[...] Read more.
This paper presents an experimental method for testing composite insulators based on vibration testing. The method used investigated the propagation, signal shape, and distortion of excited mechanical waves under the influence of defects. The aim of the method was to identify defects in the core of a composite insulator that cannot be economically detected by currently available diagnostic methods in field conditions. Therefore, this experiment aimed to distinguish between the mechanical waves’ characteristics of damaged and intact insulators using inexpensive tools. This article seeks to provide a basis for mechanical vibration diagnostics of composite insulators by demonstrating that damage to the core can result in a perceptible difference in the characteristics of mechanical waves when testing within the frequency range of audible sound.
Full article

Figure 1
Figure 1
<p>(<b>a</b>) Long-rod insulator on a transmission line [<a href="#B3-vibration-07-00057" class="html-bibr">3</a>]; (<b>b</b>) hollow-core insulators in a substation [<a href="#B1-vibration-07-00057" class="html-bibr">1</a>].</p> Full article ">Figure 2
<p>Structure of a composite insulator.</p> Full article ">Figure 3
<p>The measurement setup.</p> Full article ">Figure 4
<p>Photos taken during the measurement.</p> Full article ">Figure 5
<p>Degradation stages of the insulators.</p> Full article ">Figure 6
<p>Cumulative energy curves of insulator Type 1.</p> Full article ">Figure 7
<p>Signal waveforms in the time domain of insulator Type 1.</p> Full article ">Figure 8
<p>Spectra of insulator Type 1.</p> Full article ">Figure 9
<p>Cumulative energy curves of insulator Type 2.</p> Full article ">Figure 10
<p>Spectra of insulator Type 2.</p> Full article ">Figure 11
<p>Cumulative energy curves of insulator Type 1.</p> Full article ">Figure 12
<p>Signal waveforms in the time domain of insulator Type 1.</p> Full article ">Figure 13
<p>Spectra of insulator Type 1.</p> Full article ">Figure 14
<p>Signal waveform in the time domain of insulator Type 2.</p> Full article ">Figure 15
<p>Spectra of insulator Type 2, zoomed to 0–750 Hz range.</p> Full article ">
<p>(<b>a</b>) Long-rod insulator on a transmission line [<a href="#B3-vibration-07-00057" class="html-bibr">3</a>]; (<b>b</b>) hollow-core insulators in a substation [<a href="#B1-vibration-07-00057" class="html-bibr">1</a>].</p> Full article ">Figure 2
<p>Structure of a composite insulator.</p> Full article ">Figure 3
<p>The measurement setup.</p> Full article ">Figure 4
<p>Photos taken during the measurement.</p> Full article ">Figure 5
<p>Degradation stages of the insulators.</p> Full article ">Figure 6
<p>Cumulative energy curves of insulator Type 1.</p> Full article ">Figure 7
<p>Signal waveforms in the time domain of insulator Type 1.</p> Full article ">Figure 8
<p>Spectra of insulator Type 1.</p> Full article ">Figure 9
<p>Cumulative energy curves of insulator Type 2.</p> Full article ">Figure 10
<p>Spectra of insulator Type 2.</p> Full article ">Figure 11
<p>Cumulative energy curves of insulator Type 1.</p> Full article ">Figure 12
<p>Signal waveforms in the time domain of insulator Type 1.</p> Full article ">Figure 13
<p>Spectra of insulator Type 1.</p> Full article ">Figure 14
<p>Signal waveform in the time domain of insulator Type 2.</p> Full article ">Figure 15
<p>Spectra of insulator Type 2, zoomed to 0–750 Hz range.</p> Full article ">
Open AccessArticle
Numerical Investigation of the Nonlinear Drill String Dynamics Under Stick–Slip Vibration
by
Mohammad Javad Moharrami, Hodjat Shiri and Clóvis de Arruda Martins
Vibration 2024, 7(4), 1086-1110; https://doi.org/10.3390/vibration7040056 - 15 Nov 2024
Abstract
►▼
Show Figures
This paper presents a comprehensive analysis of the influence of rotary table velocity, weight-on-bit, and viscous damping on the drill string stick–slip vibration. The analysis allows for studying the qualitative and quantitative variation of the dynamic response of the drill pipes and drill
[...] Read more.
This paper presents a comprehensive analysis of the influence of rotary table velocity, weight-on-bit, and viscous damping on the drill string stick–slip vibration. The analysis allows for studying the qualitative and quantitative variation of the dynamic response of the drill pipes and drill collars/bit. To achieve this goal, a robust and practical finite element (FE) model of the full-scaled drill string was developed based on a velocity-weakening formulation of the nonlinear bit–rock interaction. A detailed investigation of damping parameters was carried out. The performance of the developed model was verified through comparisons with a lumped-parameter model and a field test example. Parametric studies on the stick–slip response of the entire drill string under different field operational conditions were conducted. The dynamical time series of the system response were analyzed in terms of the phase planes, response spectra, and descriptive statistics of the drill pipes and drill collars. The findings of the study revealed that for a realistic drill string geometry, the angular velocity (i.e., mean, peak-to-peak amplitude, and standard deviation) and dominant frequency of self-excited torsional stick–slip oscillations along the drill pipes and drill collars/bit are mainly governed by the rotary table velocity. Furthermore, it was shown that the contribution of higher harmonics in the torsional stick–slip response of the drill pipes is more substantial than the drill collars/bit.
Full article
Figure 1
Figure 1
<p>Schematic of a typical offshore drilling system.</p> Full article ">Figure 2
<p>A sketch of the considered full drill string (<b>left</b>) and the corresponding FEM model developed in ABAQUS with boundary conditions at the surface and the bit (<b>right</b>).</p> Full article ">Figure 3
<p>Effect of frequency band on the Rayleigh damping variations.</p> Full article ">Figure 4
<p>Lumped-parameter model representation of the drill string.</p> Full article ">Figure 5
<p>Friction model at the bit: switch friction model (enhanced Karnopp friction model) + Stribeck model.</p> Full article ">Figure 6
<p>Example stick–slip time series and phase planes of the bit angular velocity obtained from (<b>a</b>) the FEM model and (<b>b</b>) the lumped-parameter model using Equations (7) and (11) with parameter values given in <a href="#vibration-07-00056-t003" class="html-table">Table 3</a>. <span class="html-italic">Ω<sub>r</sub></span> = 7.33 rad/s (dashed lines), <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> = 0.03 (with <span class="html-italic">α</span> = 0.070416 1/s and <span class="html-italic">β</span> = 0.00132142 s).</p> Full article ">Figure 7
<p>Example of stick–slip vibration occurring in the field test under constant rotational velocity <span class="html-italic">Ω<sub>r</sub></span> = 9.42 rad/s. Field test result from [<a href="#B48-vibration-07-00056" class="html-bibr">48</a>].</p> Full article ">Figure 8
<p>Definition of the peak-to-peak amplitude (2<span class="html-italic">A</span>) of angular velocity under stick–slip conditions for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> = 40 kN.</p> Full article ">Figure 9
<p>Time series and phase planes of the angular velocity at the drill bit for <span class="html-italic">W<sub>b</sub></span> = 40 kN, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">Ω<sub>r</sub></span> of (<b>a</b>) 2.09, (<b>b</b>) 5.24, (<b>c</b>) 7.33, and (<b>d</b>) 11.52 rad/s.</p> Full article ">Figure 10
<p>Time series and phase planes of the angular velocity at 1900 m above the drill bit for <span class="html-italic">W<sub>b</sub></span> = 40 kN, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">Ω<sub>r</sub></span> of (<b>a</b>) 2.09, (<b>b</b>) 5.24, (<b>c</b>) 7.33, and (<b>d</b>) 11.52 rad/s.</p> Full article ">Figure 11
<p>Response spectra of angular velocity at the drill bit (<b>left</b>) and 1900 m above the bit (<b>right</b>) with <span class="html-italic">W<sub>b</sub></span> = 40 kN, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">Ω<sub>r</sub></span> of (<b>a</b>) 2.09, (<b>b</b>) 5.24, (<b>c</b>) 7.33, and (<b>d</b>) 11.52 rad/s. Dashed lines indicate natural frequencies.</p> Full article ">Figure 12
<p>Time series and phase planes of the angular velocity at the bit for <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> of (<b>a</b>) 10, (<b>b</b>) 30, (<b>c</b>) 40, and (<b>d</b>) 50 kN.</p> Full article ">Figure 13
<p>Time series and phase planes of the angular velocity at 1650 m above the bit for <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> of (<b>a</b>) 10, (<b>b</b>) 30, (<b>c</b>) 40, and (<b>d</b>) 50 kN.</p> Full article ">Figure 14
<p>Response spectra of angular velocity at the drill bit (<b>left</b>) and 1650 m above the bit (<b>right</b>) for <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> of (<b>a</b>) 10 kN, (<b>b</b>) 30 kN, (<b>c</b>) 40 kN, and (<b>d</b>) 50 kN. Dashed lines indicate natural frequencies.</p> Full article ">Figure 15
<p>Time series and phase planes of the angular velocity at the bit for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.05, (<b>b</b>) 0.10, (<b>c</b>) 0.20, (<b>d</b>) 0.27, and 0.30.</p> Full article ">Figure 16
<p>Time series and phase planes of the angular velocity at 1400 m above the bit for <span class="html-italic">Ω</span><sub>r</sub> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.05, (<b>b</b>) 0.10, (<b>c</b>) 0.20, (<b>d</b>) 0.27, and 0.30.</p> Full article ">Figure 17
<p>Response spectra of angular velocity at the drill bit (<b>left</b>) and 1400 m above the bit (<b>right</b>) for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.05, (<b>b</b>) 0.10, (<b>c</b>) 0.20, and (<b>d</b>) 0.27.</p> Full article ">Figure 18
<p>Time series (<b>left</b>) and phase planes (<b>right</b>) of the bit response obtained from the FEM model (solid lines) and the lumped-parameter model (dashed lines) for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.10 and (<b>b</b>) 0.13.</p> Full article ">Figure 19
<p>Variation of the peak-to-peak amplitude of angular velocity along the drill string under different stick–slip conditions. (<b>a</b>) <span class="html-italic">W<sub>b</sub></span> = 40 kN and <span class="html-italic">ξ</span> = 0.03, (<b>b</b>) <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s and <span class="html-italic">ξ</span> = 0.03, and (<b>c</b>) <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s and <span class="html-italic">W<sub>b</sub></span> = 40 kN.</p> Full article ">Figure 20
<p>Variation of the standard deviation of angular velocity along the drill string under different stick–slip conditions. (<b>a</b>) <span class="html-italic">W<sub>b</sub></span> = 40 kN and <span class="html-italic">ξ</span> = 0.03, (<b>b</b>) <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s and <span class="html-italic">ξ</span> = 0.03, and (<b>c</b>) <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s and <span class="html-italic">W<sub>b</sub></span> = 40 kN.</p> Full article ">
<p>Schematic of a typical offshore drilling system.</p> Full article ">Figure 2
<p>A sketch of the considered full drill string (<b>left</b>) and the corresponding FEM model developed in ABAQUS with boundary conditions at the surface and the bit (<b>right</b>).</p> Full article ">Figure 3
<p>Effect of frequency band on the Rayleigh damping variations.</p> Full article ">Figure 4
<p>Lumped-parameter model representation of the drill string.</p> Full article ">Figure 5
<p>Friction model at the bit: switch friction model (enhanced Karnopp friction model) + Stribeck model.</p> Full article ">Figure 6
<p>Example stick–slip time series and phase planes of the bit angular velocity obtained from (<b>a</b>) the FEM model and (<b>b</b>) the lumped-parameter model using Equations (7) and (11) with parameter values given in <a href="#vibration-07-00056-t003" class="html-table">Table 3</a>. <span class="html-italic">Ω<sub>r</sub></span> = 7.33 rad/s (dashed lines), <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> = 0.03 (with <span class="html-italic">α</span> = 0.070416 1/s and <span class="html-italic">β</span> = 0.00132142 s).</p> Full article ">Figure 7
<p>Example of stick–slip vibration occurring in the field test under constant rotational velocity <span class="html-italic">Ω<sub>r</sub></span> = 9.42 rad/s. Field test result from [<a href="#B48-vibration-07-00056" class="html-bibr">48</a>].</p> Full article ">Figure 8
<p>Definition of the peak-to-peak amplitude (2<span class="html-italic">A</span>) of angular velocity under stick–slip conditions for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> = 40 kN.</p> Full article ">Figure 9
<p>Time series and phase planes of the angular velocity at the drill bit for <span class="html-italic">W<sub>b</sub></span> = 40 kN, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">Ω<sub>r</sub></span> of (<b>a</b>) 2.09, (<b>b</b>) 5.24, (<b>c</b>) 7.33, and (<b>d</b>) 11.52 rad/s.</p> Full article ">Figure 10
<p>Time series and phase planes of the angular velocity at 1900 m above the drill bit for <span class="html-italic">W<sub>b</sub></span> = 40 kN, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">Ω<sub>r</sub></span> of (<b>a</b>) 2.09, (<b>b</b>) 5.24, (<b>c</b>) 7.33, and (<b>d</b>) 11.52 rad/s.</p> Full article ">Figure 11
<p>Response spectra of angular velocity at the drill bit (<b>left</b>) and 1900 m above the bit (<b>right</b>) with <span class="html-italic">W<sub>b</sub></span> = 40 kN, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">Ω<sub>r</sub></span> of (<b>a</b>) 2.09, (<b>b</b>) 5.24, (<b>c</b>) 7.33, and (<b>d</b>) 11.52 rad/s. Dashed lines indicate natural frequencies.</p> Full article ">Figure 12
<p>Time series and phase planes of the angular velocity at the bit for <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> of (<b>a</b>) 10, (<b>b</b>) 30, (<b>c</b>) 40, and (<b>d</b>) 50 kN.</p> Full article ">Figure 13
<p>Time series and phase planes of the angular velocity at 1650 m above the bit for <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> of (<b>a</b>) 10, (<b>b</b>) 30, (<b>c</b>) 40, and (<b>d</b>) 50 kN.</p> Full article ">Figure 14
<p>Response spectra of angular velocity at the drill bit (<b>left</b>) and 1650 m above the bit (<b>right</b>) for <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s, <span class="html-italic">ξ</span> = 0.03, and <span class="html-italic">W<sub>b</sub></span> of (<b>a</b>) 10 kN, (<b>b</b>) 30 kN, (<b>c</b>) 40 kN, and (<b>d</b>) 50 kN. Dashed lines indicate natural frequencies.</p> Full article ">Figure 15
<p>Time series and phase planes of the angular velocity at the bit for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.05, (<b>b</b>) 0.10, (<b>c</b>) 0.20, (<b>d</b>) 0.27, and 0.30.</p> Full article ">Figure 16
<p>Time series and phase planes of the angular velocity at 1400 m above the bit for <span class="html-italic">Ω</span><sub>r</sub> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.05, (<b>b</b>) 0.10, (<b>c</b>) 0.20, (<b>d</b>) 0.27, and 0.30.</p> Full article ">Figure 17
<p>Response spectra of angular velocity at the drill bit (<b>left</b>) and 1400 m above the bit (<b>right</b>) for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.05, (<b>b</b>) 0.10, (<b>c</b>) 0.20, and (<b>d</b>) 0.27.</p> Full article ">Figure 18
<p>Time series (<b>left</b>) and phase planes (<b>right</b>) of the bit response obtained from the FEM model (solid lines) and the lumped-parameter model (dashed lines) for <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s, <span class="html-italic">W<sub>b</sub></span> = 40 kN, and <span class="html-italic">ξ</span> of (<b>a</b>) 0.10 and (<b>b</b>) 0.13.</p> Full article ">Figure 19
<p>Variation of the peak-to-peak amplitude of angular velocity along the drill string under different stick–slip conditions. (<b>a</b>) <span class="html-italic">W<sub>b</sub></span> = 40 kN and <span class="html-italic">ξ</span> = 0.03, (<b>b</b>) <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s and <span class="html-italic">ξ</span> = 0.03, and (<b>c</b>) <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s and <span class="html-italic">W<sub>b</sub></span> = 40 kN.</p> Full article ">Figure 20
<p>Variation of the standard deviation of angular velocity along the drill string under different stick–slip conditions. (<b>a</b>) <span class="html-italic">W<sub>b</sub></span> = 40 kN and <span class="html-italic">ξ</span> = 0.03, (<b>b</b>) <span class="html-italic">Ω<sub>r</sub></span> = 6.3 rad/s and <span class="html-italic">ξ</span> = 0.03, and (<b>c</b>) <span class="html-italic">Ω<sub>r</sub></span> = 5.24 rad/s and <span class="html-italic">W<sub>b</sub></span> = 40 kN.</p> Full article ">
Open AccessArticle
Modular Modeling of a Half-Vehicle System Using Generalized Receptance Coupling and Frequency-Based Substructuring (GRCFBS)
by
Behzad Hamedi and Saied Taheri
Vibration 2024, 7(4), 1063-1085; https://doi.org/10.3390/vibration7040055 - 11 Nov 2024
Cited by 2
Abstract
►▼
Show Figures
This paper presents an advanced modular modeling approach for vertical vibration analysis of dynamic systems using the Generalized Receptance Coupling and Frequency-Based Substructuring (GRCFBS) method. The focus is on a four-DoF half-vehicle model comprising three key subsystems: front suspension, rear suspension, and the
[...] Read more.
This paper presents an advanced modular modeling approach for vertical vibration analysis of dynamic systems using the Generalized Receptance Coupling and Frequency-Based Substructuring (GRCFBS) method. The focus is on a four-DoF half-vehicle model comprising three key subsystems: front suspension, rear suspension, and the vehicle’s trimmed body. The proposed technique is designed to predict dynamic responses in reconfigurable systems across various applications, including automotive, robotics, mechanical machinery, and aerospace structures. By coupling the receptance matrices (FRFs) of individual vehicle modules, the overall system receptance matrix is efficiently derived in a disassembled configuration. Two generalized coupling methods, originally developed by Jetmundsen and D.D. Klerk, are employed to determine the complete vehicle’s receptance matrix from its subsystems. Validation is achieved by comparing the results with established methods, such as direct solution and modal analysis, demonstrating high accuracy and reliability for complex dynamic systems. This modular approach allows for the creation of reduced-order models focused on key measurement points without the need for detailed system representation. The method offers significant advantages in early-stage vehicle development, providing critical insights into system vibration behavior.
Full article
Figure 1
Figure 1
<p>Half-car model.</p> Full article ">Figure 2
<p>Initial substructuring scheme of a car system to three substructures.</p> Full article ">Figure 3
<p>Reduced-order substructuring scheme to two substructures.</p> Full article ">Figure 4
<p>Magnitude and phase graph: receptance component of H11.</p> Full article ">Figure 5
<p>Magnitude and phase graph: receptance component of H22.</p> Full article ">Figure 6
<p>Magnitude and phase graph: receptance component of H33.</p> Full article ">Figure 7
<p>Magnitude and phase graph: receptance component of H44.</p> Full article ">Figure 8
<p>Magnitude and phase graph: receptance component of H13.</p> Full article ">Figure 9
<p>Magnitude and phase graph: receptance component of H31.</p> Full article ">Figure 10
<p>Magnitude and phase graph: receptance component of H42.</p> Full article ">Figure 11
<p>Magnitude and phase graph: receptance component of H24.</p> Full article ">Figure 12
<p>Magnitude and phase graph: receptance component of H21.</p> Full article ">Figure 13
<p>Magnitude and phase graph: receptance component of H12.</p> Full article ">
<p>Half-car model.</p> Full article ">Figure 2
<p>Initial substructuring scheme of a car system to three substructures.</p> Full article ">Figure 3
<p>Reduced-order substructuring scheme to two substructures.</p> Full article ">Figure 4
<p>Magnitude and phase graph: receptance component of H11.</p> Full article ">Figure 5
<p>Magnitude and phase graph: receptance component of H22.</p> Full article ">Figure 6
<p>Magnitude and phase graph: receptance component of H33.</p> Full article ">Figure 7
<p>Magnitude and phase graph: receptance component of H44.</p> Full article ">Figure 8
<p>Magnitude and phase graph: receptance component of H13.</p> Full article ">Figure 9
<p>Magnitude and phase graph: receptance component of H31.</p> Full article ">Figure 10
<p>Magnitude and phase graph: receptance component of H42.</p> Full article ">Figure 11
<p>Magnitude and phase graph: receptance component of H24.</p> Full article ">Figure 12
<p>Magnitude and phase graph: receptance component of H21.</p> Full article ">Figure 13
<p>Magnitude and phase graph: receptance component of H12.</p> Full article ">
Open AccessSystematic Review
Vibration Signal Analysis for Intelligent Rotating Machinery Diagnosis and Prognosis: A Comprehensive Systematic Literature Review
by
Ikram Bagri, Karim Tahiry, Aziz Hraiba, Achraf Touil and Ahmed Mousrij
Vibration 2024, 7(4), 1013-1062; https://doi.org/10.3390/vibration7040054 - 31 Oct 2024
Cited by 1
Abstract
►▼
Show Figures
Many industrial processes, from manufacturing to food processing, incorporate rotating elements as principal components in their production chain. Failure of these components often leads to costly downtime and potential safety risks, further emphasizing the importance of monitoring their health state. Vibration signal analysis
[...] Read more.
Many industrial processes, from manufacturing to food processing, incorporate rotating elements as principal components in their production chain. Failure of these components often leads to costly downtime and potential safety risks, further emphasizing the importance of monitoring their health state. Vibration signal analysis is now a common approach for this purpose, as it provides useful information related to the dynamic behavior of machines. This research aimed to conduct a comprehensive examination of the current methodologies employed in the stages of vibration signal analysis, which encompass preprocessing, processing, and post-processing phases, ultimately leading to the application of Artificial Intelligence-based diagnostics and prognostics. An extensive search was conducted in various databases, including ScienceDirect, IEEE, MDPI, Springer, and Google Scholar, from 2020 to early 2024 following the PRISMA guidelines. Articles that aligned with at least one of the targeted topics cited above and provided unique methods and explicit results qualified for retention, while those that were redundant or did not meet the established inclusion criteria were excluded. Subsequently, 270 articles were selected from an initial pool of 338. The review results highlighted several deficiencies in the preprocessing step and the experimental validation, with implementation rates of 15.41% and 10.15%, respectively, in the selected prototype studies. Examination of the processing phase revealed that time scale decomposition methods have become essential for accurate analysis of vibration signals, as they facilitate the extraction of complex information that remains obscured in the original, undecomposed signals. Combining such methods with time–frequency analysis methods was shown to be an ideal combination for information extraction. In the context of fault detection, support vector machines (SVMs), convolutional neural networks (CNNs), Long Short-Term Memory (LSTM) networks, k-nearest neighbors (KNN), and random forests have been identified as the five most frequently employed algorithms. Meanwhile, transformer-based models are emerging as a promising venue for the prediction of RUL values, along with data transformation. Given the conclusions drawn, future researchers are urged to investigate the interpretability and integration of the diagnosis and prognosis models developed with the aim of applying them in real-time industrial contexts. Furthermore, there is a need for experimental studies to disclose the preprocessing details for datasets and the operational conditions of the machinery, thereby improving the data reproducibility. Another area that warrants further investigation is differentiation of the various types of fault information present in vibration signals obtained from bearings, as the defect information from the overall system is embedded within these signals.
Full article
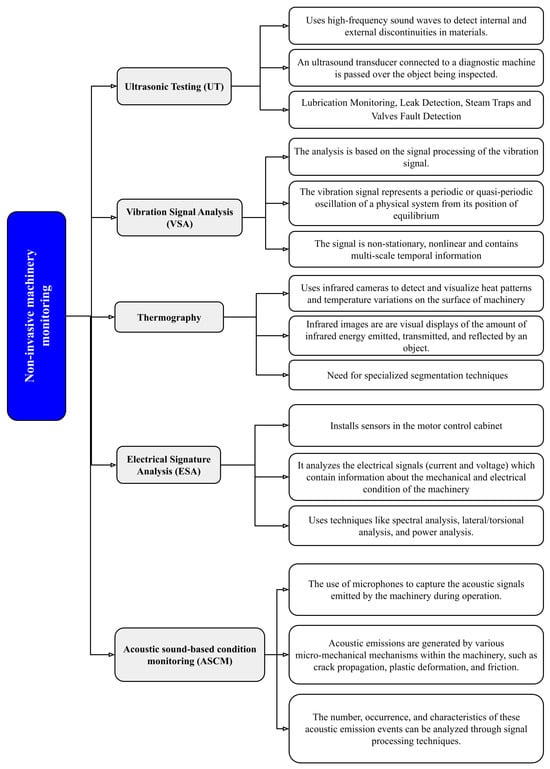
Figure 1
Figure 1
<p>Non-intrusive monitoring approaches for rotating machinery.</p> Full article ">Figure 2
<p>Global process of fault detection through NDTs.</p> Full article ">Figure 3
<p>PRISMA flow diagram [<a href="#B22-vibration-07-00054" class="html-bibr">22</a>].</p> Full article ">Figure 4
<p>Overall flowchart of the methodology.</p> Full article ">Figure 5
<p>Concept map of the term concepts researched.</p> Full article ">Figure 6
<p>Types of studies retrieved.</p> Full article ">Figure 7
<p>Studies retrieved per keyword.</p> Full article ">Figure 8
<p>UpSet plot of the distribution of data across different categories.</p> Full article ">Figure 9
<p>Evolution of the studies retrieved.</p> Full article ">Figure 10
<p>Signal processing methods.</p> Full article ">Figure 11
<p>Heatmap of signal processing techniques and their use from 2020 to 2023 in the selected studies.</p> Full article ">Figure 12
<p>Signal post-processing methods.</p> Full article ">Figure 13
<p>Machine learning methods.</p> Full article ">Figure 14
<p>Frequency of use of machine learning algorithms in the studies reviewed.</p> Full article ">Figure 15
<p>Bubble chart depicting the relationship between the complexity and accuracy of the algorithms discussed regarding their computational cost (bubble size).</p> Full article ">
<p>Non-intrusive monitoring approaches for rotating machinery.</p> Full article ">Figure 2
<p>Global process of fault detection through NDTs.</p> Full article ">Figure 3
<p>PRISMA flow diagram [<a href="#B22-vibration-07-00054" class="html-bibr">22</a>].</p> Full article ">Figure 4
<p>Overall flowchart of the methodology.</p> Full article ">Figure 5
<p>Concept map of the term concepts researched.</p> Full article ">Figure 6
<p>Types of studies retrieved.</p> Full article ">Figure 7
<p>Studies retrieved per keyword.</p> Full article ">Figure 8
<p>UpSet plot of the distribution of data across different categories.</p> Full article ">Figure 9
<p>Evolution of the studies retrieved.</p> Full article ">Figure 10
<p>Signal processing methods.</p> Full article ">Figure 11
<p>Heatmap of signal processing techniques and their use from 2020 to 2023 in the selected studies.</p> Full article ">Figure 12
<p>Signal post-processing methods.</p> Full article ">Figure 13
<p>Machine learning methods.</p> Full article ">Figure 14
<p>Frequency of use of machine learning algorithms in the studies reviewed.</p> Full article ">Figure 15
<p>Bubble chart depicting the relationship between the complexity and accuracy of the algorithms discussed regarding their computational cost (bubble size).</p> Full article ">
Open AccessArticle
Active Vibration Control Performance Comparison Based on Middle Pedestal Stiffness Using a Mobility Model and the Narrowband Fx-LMS Technique
by
Anmok Jeong, Kyuchul Jung, Youngcheol Park, Junyeong Heo and Hakjun Lee
Vibration 2024, 7(4), 999-1012; https://doi.org/10.3390/vibration7040053 - 29 Oct 2024
Abstract
►▼
Show Figures
Vibrations generated from equipment mounted on ships radiate into the water and affect covert operation capabilities. Accordingly, various studies are being conducted to reduce vibration transmitted from mounted equipment. In this study, a system consisting of mounting equipment, a 3-axis active mount, a
[...] Read more.
Vibrations generated from equipment mounted on ships radiate into the water and affect covert operation capabilities. Accordingly, various studies are being conducted to reduce vibration transmitted from mounted equipment. In this study, a system consisting of mounting equipment, a 3-axis active mount, a middle pedestal, and a lower mount of the middle pedestal was modeled using a finite element analysis program, and a mobility model was constructed by calculating the frequency response function between the positions required for analysis. The error signal (primary path) obtained using the mobility model and the response at the operating point by the control force of the actuator (secondary path) are applied to the narrowband Fx-LMS algorithm for vibration control, and the control performance was compared. Through coupling analysis of the middle pedestal, the control influence according to the rigidity of the middle pedestal was analyzed. As a result of the control simulation, the time required for vibration control was controlled approximately 6 times faster in the model, with increased stiffness of the middle pedestal, and the vibration reduction performance was predicted to improve by a minimum of 0.9 dB and a maximum of 13.3 dB. Through this study, a simulation model that can provide a guide for the design of the middle pedestal of a ship was obtained, and it is expected that it can be utilized for a preliminary design review before manufacturing the middle pedestal of a ship.
Full article
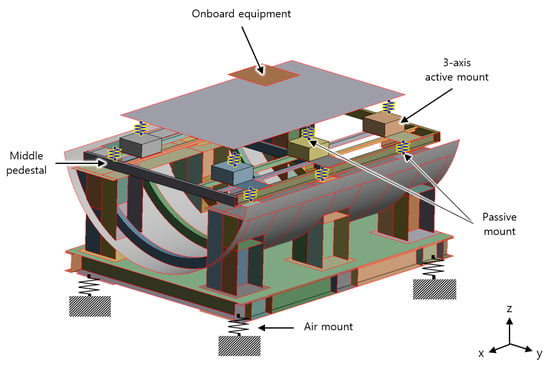
Figure 1
Figure 1
<p>Ship vibration reduction test equipment.</p> Full article ">Figure 2
<p>3-axis active mount configuration (front view).</p> Full article ">Figure 3
<p>Mechanism for vibration reduction.</p> Full article ">Figure 4
<p>FEM modeling and boundary condition.</p> Full article ">Figure 5
<p>Block diagram of Fx-LMS.</p> Full article ">Figure 6
<p>Vibration control simulation process for ship vibration reduction test equipment.</p> Full article ">Figure 7
<p>Excitation point and response point for primary path signal acquisition.</p> Full article ">Figure 8
<p>Excitation point and response point for secondary path signal acquisition.</p> Full article ">Figure 9
<p>Characteristic curve of inertial actuator.</p> Full article ">Figure 10
<p>Excitation and response position for coupling analysis of middle pedestal.</p> Full article ">Figure 11
<p>Response at active mount position 1~3 when exciting active mount 1 in the x direction (Case 1).</p> Full article ">Figure 12
<p>Response at active mount position 1~3 when exciting active mount 1 in the z direction (Case 1).</p> Full article ">Figure 13
<p>Response at active mount position 1~3 when exciting active mount 1 in the x direction. (<b>a</b>) Case 1 (<b>left</b>: frequency response, <b>right</b>: phase angle), (<b>b</b>) Case 2 (<b>left</b>: frequency response, <b>right</b>: phase angle).</p> Full article ">Figure 14
<p>Control results according to the middle pedestal stiffness.</p> Full article ">
<p>Ship vibration reduction test equipment.</p> Full article ">Figure 2
<p>3-axis active mount configuration (front view).</p> Full article ">Figure 3
<p>Mechanism for vibration reduction.</p> Full article ">Figure 4
<p>FEM modeling and boundary condition.</p> Full article ">Figure 5
<p>Block diagram of Fx-LMS.</p> Full article ">Figure 6
<p>Vibration control simulation process for ship vibration reduction test equipment.</p> Full article ">Figure 7
<p>Excitation point and response point for primary path signal acquisition.</p> Full article ">Figure 8
<p>Excitation point and response point for secondary path signal acquisition.</p> Full article ">Figure 9
<p>Characteristic curve of inertial actuator.</p> Full article ">Figure 10
<p>Excitation and response position for coupling analysis of middle pedestal.</p> Full article ">Figure 11
<p>Response at active mount position 1~3 when exciting active mount 1 in the x direction (Case 1).</p> Full article ">Figure 12
<p>Response at active mount position 1~3 when exciting active mount 1 in the z direction (Case 1).</p> Full article ">Figure 13
<p>Response at active mount position 1~3 when exciting active mount 1 in the x direction. (<b>a</b>) Case 1 (<b>left</b>: frequency response, <b>right</b>: phase angle), (<b>b</b>) Case 2 (<b>left</b>: frequency response, <b>right</b>: phase angle).</p> Full article ">Figure 14
<p>Control results according to the middle pedestal stiffness.</p> Full article ">
Open AccessArticle
Unidirectional Flow Through Time-Dependent Cross-Sectional Areas of a Compliant Tube and a Valve: A Nonlinear Model
by
Christos Manopoulos, Sokrates Tsangaris, Christina Georgantopoulou and Dimitrios Mathioulakis
Vibration 2024, 7(4), 987-998; https://doi.org/10.3390/vibration7040052 - 29 Oct 2024
Abstract
This work investigates the conditions for net flow generation by a straight tube with a cross-sectional area harmonically varying in time that connects two tanks—a problem that is mainly found in the design of impedance pumps. By assuming a quasi-one-dimensional flow and applying
[...] Read more.
This work investigates the conditions for net flow generation by a straight tube with a cross-sectional area harmonically varying in time that connects two tanks—a problem that is mainly found in the design of impedance pumps. By assuming a quasi-one-dimensional flow and applying continuity and momentum equations, a first-order differential equation with respect to the flow rate is derived and presented for the first time, including a nonlinear term that is responsible for net flow rate generation. Namely, the net flow rate is found to be nonzero (as is the nonlinear term) if the cross-sectional areas of the two tanks are unequal and one of them is smaller than that of the straight tube. In this case, the flow is directed from the smaller to the larger tank and the net flow rate increases with the frequency of the tube’s cross-sectional area variation. In contrast, when the tanks’ cross-sections are equal, the net flow is generated only if a valve is installed, e.g., at one end of the tube, due to the large asymmetries imposed in the hydraulic losses with respect to the tube mid-length. Compared with constant valve opening, the net flow rate is augmented significantly if the valve opening is time-dependent. By employing the same equation, the flow rate of an intra-aortic counter-pulsating balloon pump is also examined, in which the valve (representing the aortic valve) opens during the shrinkage of the tube, and it is shown that the net flow rate increases with the frequency and amplitude of the tube’s cross-sectional area. Conclusively, the harmonic oscillation in time of a tube’s wall can cause unidirectional flow only if asymmetric losses are present with respect to its mid-length.
Full article
(This article belongs to the Special Issue Nonlinear Vibration of Mechanical Systems)
►▼
Show Figures
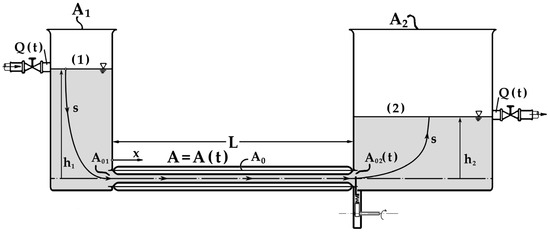
Figure 1
Figure 1
<p>Hydraulic installation.</p> Full article ">Figure 2
<p>Gate valve loss coefficient [<a href="#B24-vibration-07-00052" class="html-bibr">24</a>] (p. 273).</p> Full article ">Figure 3
<p>Net flow rate versus tank cross-sectional areas. <span class="html-italic">W</span> = 5, <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>A</mi> </mrow> <mo>~</mo> </mover> </mrow> <mrow> <mi>b</mi> </mrow> </msub> <mo>=</mo> <mn>0.1</mn> </mrow> </semantics></math>.</p> Full article ">Figure 4
<p>Net flow rate versus Womersley number.</p> Full article ">Figure 5
<p>Net flow rate versus valve loss coefficient. Valve opening constant.</p> Full article ">Figure 6
<p>Tube (dashed line) and gate valve (continuous line) cross-sectional areas versus non-dimensional time. <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi mathvariant="normal">A</mi> </mrow> <mo>~</mo> </mover> </mrow> <mrow> <mn>02</mn> <mo>,</mo> <mi mathvariant="normal">m</mi> <mi mathvariant="normal">i</mi> <mi mathvariant="normal">n</mi> </mrow> </msub> <mo>=</mo> <mn>0.084</mn> </mrow> </semantics></math>.</p> Full article ">Figure 7
<p>Net flow rate versus valve minimum cross-sectional area. Static and dynamic cases.</p> Full article ">Figure 8
<p>Dimensionless net flow rate versus <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi mathvariant="normal">A</mi> </mrow> <mo>~</mo> </mover> </mrow> <mrow> <mi mathvariant="normal">b</mi> </mrow> </msub> </mrow> </semantics></math> and <span class="html-italic">W</span>.</p> Full article ">Figure 9
<p>Net flow rate versus frequency and tube oscillation amplitude.</p> Full article ">
<p>Hydraulic installation.</p> Full article ">Figure 2
<p>Gate valve loss coefficient [<a href="#B24-vibration-07-00052" class="html-bibr">24</a>] (p. 273).</p> Full article ">Figure 3
<p>Net flow rate versus tank cross-sectional areas. <span class="html-italic">W</span> = 5, <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi>A</mi> </mrow> <mo>~</mo> </mover> </mrow> <mrow> <mi>b</mi> </mrow> </msub> <mo>=</mo> <mn>0.1</mn> </mrow> </semantics></math>.</p> Full article ">Figure 4
<p>Net flow rate versus Womersley number.</p> Full article ">Figure 5
<p>Net flow rate versus valve loss coefficient. Valve opening constant.</p> Full article ">Figure 6
<p>Tube (dashed line) and gate valve (continuous line) cross-sectional areas versus non-dimensional time. <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi mathvariant="normal">A</mi> </mrow> <mo>~</mo> </mover> </mrow> <mrow> <mn>02</mn> <mo>,</mo> <mi mathvariant="normal">m</mi> <mi mathvariant="normal">i</mi> <mi mathvariant="normal">n</mi> </mrow> </msub> <mo>=</mo> <mn>0.084</mn> </mrow> </semantics></math>.</p> Full article ">Figure 7
<p>Net flow rate versus valve minimum cross-sectional area. Static and dynamic cases.</p> Full article ">Figure 8
<p>Dimensionless net flow rate versus <math display="inline"><semantics> <mrow> <msub> <mrow> <mover accent="true"> <mrow> <mi mathvariant="normal">A</mi> </mrow> <mo>~</mo> </mover> </mrow> <mrow> <mi mathvariant="normal">b</mi> </mrow> </msub> </mrow> </semantics></math> and <span class="html-italic">W</span>.</p> Full article ">Figure 9
<p>Net flow rate versus frequency and tube oscillation amplitude.</p> Full article ">
Open AccessArticle
A Mechanical Fault Identification Method for On-Load Tap Changers Based on Hybrid Time—Frequency Graphs of Vibration Signals and DSCNN-SVM with Small Sample Sizes
by
Yanhui Shi, Yanjun Ruan, Liangchuang Li, Bo Zhang, Yichao Huang, Mao Xia, Kaiwen Yuan, Zhao Luo and Sizhao Lu
Vibration 2024, 7(4), 970-986; https://doi.org/10.3390/vibration7040051 - 28 Oct 2024
Cited by 1
Abstract
►▼
Show Figures
In engineering applications, the accuracy of on-load tap changer (OLTC) mechanical fault identification methods based on vibration signals is constrained by the quantity and quality of the samples. Therefore, a novel small-sample-size OLTC mechanical fault identification method incorporating short-time Fourier transform (STFT), synchrosqueezed
[...] Read more.
In engineering applications, the accuracy of on-load tap changer (OLTC) mechanical fault identification methods based on vibration signals is constrained by the quantity and quality of the samples. Therefore, a novel small-sample-size OLTC mechanical fault identification method incorporating short-time Fourier transform (STFT), synchrosqueezed wavelet transform (SWT), a dual-stream convolutional neural network (DSCNN), and support vector machine (SVM) is proposed. Firstly, the one-dimensional time-series vibration signals are transformed using STFT and SWT to obtain time–frequency graphs. STFT time–frequency graphs capture the global features of the OLTC vibration signals, while SWT time–frequency graphs capture the local features of the OLTC vibration signals. Secondly, these time–frequency graphs are input into the CNN to extract key features. In the fusion layer, the feature vectors from the STFT and SWT graphs are combined to form a fusion vector that encompasses both global and local time–frequency features. Finally, the softmax classifier of the traditional CNN is replaced with an SVM classifier, and the fusion vector is input into this classifier. Compared to the traditional fault identification methods, the proposed method demonstrates higher identification accuracy and stronger generalization ability under the conditions of small sample sizes and noise interference.
Full article
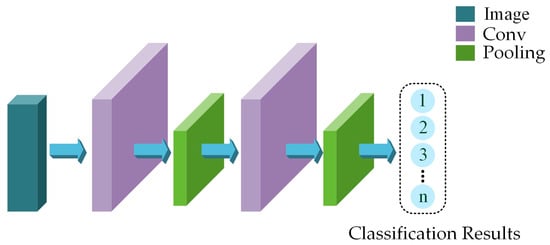
Figure 1
Figure 1
<p>Structure of CNN.</p> Full article ">Figure 2
<p>SVM classification principles: (<b>a</b>) imbalanced classes; (<b>b</b>) balanced classes.</p> Full article ">Figure 3
<p>DSCNN-SVM structure.</p> Full article ">Figure 4
<p>Identification process.</p> Full article ">Figure 5
<p>Picture of the experimental testing setup.</p> Full article ">Figure 6
<p>Sensor installation and fault condition setting: (<b>a</b>) sensor installation; (<b>b</b>) jamming; (<b>c</b>) insulated panel looseness; (<b>d</b>) lower static contact looseness; (<b>e</b>) upper static contact looseness; (<b>f</b>) moving contact looseness; (<b>g</b>) contact erosion; (<b>h</b>) contact wear.</p> Full article ">Figure 7
<p>UCG-type OLTC vibration signals under different operating conditions: (<b>a</b>) normal condition time-domain signal; (<b>b</b>) normal condition frequency-domain signal; (<b>c</b>) jamming time-domain signal; (<b>d</b>) jamming frequency-domain signal; (<b>e</b>) insulated panel looseness time-domain signal; (<b>f</b>) insulated panel frequency-domain signal; (<b>g</b>) lower static contact looseness time-domain signal; (<b>h</b>) lower static contact looseness frequency-domain signal; (<b>i</b>) upper static contact looseness time-domain signal; (<b>j</b>) upper static contact looseness frequency-domain signal; (<b>k</b>) moving contact looseness time-domain signal; (<b>l</b>) moving contact looseness frequency-domain signal; (<b>m</b>) contact erosion time-domain signal; (<b>n</b>) contact erosion frequency-domain signal; (<b>o</b>) contact wear time-domain signal;. (<b>p</b>) contact wear frequency-domain signal.</p> Full article ">Figure 8
<p>SWT time–frequency graphs: (<b>a</b>) normal; (<b>b</b>) jamming; (<b>c</b>) insulated panel looseness; (<b>d</b>) lower static contact looseness; (<b>e</b>) upper static contact looseness; (<b>f</b>) moving contact looseness; (<b>g</b>) contact erosion; (<b>h</b>) contact wear.</p> Full article ">Figure 9
<p>STFT time–frequency graphs: (<b>a</b>) Normal; (<b>b</b>) Jamming; (<b>c</b>) Insulated panel looseness; (<b>d</b>) Lower static contact looseness; (<b>e</b>) Upper static contact looseness; (<b>f</b>) Moving contact looseness; (<b>g</b>) Contact erosion; (<b>h</b>) Contact wear.</p> Full article ">Figure 10
<p>Comparison of different imaging methods.</p> Full article ">Figure 11
<p>Comparison of validation accuracy and loss function for different methods: (<b>a</b>) loss function curve; (<b>b</b>) accuracy curve.</p> Full article ">Figure 12
<p>Time–frequency graphs of OLTC vibration signals under different noise levels: (<b>a</b>) STFT time–frequency graphs without noise; (<b>b</b>) STFT time–frequency graphs with 10 db noise; (<b>c</b>) SWT time–frequency graphs without noise; (<b>d</b>) SWT time–frequency graphs with 10 db noise.</p> Full article ">
<p>Structure of CNN.</p> Full article ">Figure 2
<p>SVM classification principles: (<b>a</b>) imbalanced classes; (<b>b</b>) balanced classes.</p> Full article ">Figure 3
<p>DSCNN-SVM structure.</p> Full article ">Figure 4
<p>Identification process.</p> Full article ">Figure 5
<p>Picture of the experimental testing setup.</p> Full article ">Figure 6
<p>Sensor installation and fault condition setting: (<b>a</b>) sensor installation; (<b>b</b>) jamming; (<b>c</b>) insulated panel looseness; (<b>d</b>) lower static contact looseness; (<b>e</b>) upper static contact looseness; (<b>f</b>) moving contact looseness; (<b>g</b>) contact erosion; (<b>h</b>) contact wear.</p> Full article ">Figure 7
<p>UCG-type OLTC vibration signals under different operating conditions: (<b>a</b>) normal condition time-domain signal; (<b>b</b>) normal condition frequency-domain signal; (<b>c</b>) jamming time-domain signal; (<b>d</b>) jamming frequency-domain signal; (<b>e</b>) insulated panel looseness time-domain signal; (<b>f</b>) insulated panel frequency-domain signal; (<b>g</b>) lower static contact looseness time-domain signal; (<b>h</b>) lower static contact looseness frequency-domain signal; (<b>i</b>) upper static contact looseness time-domain signal; (<b>j</b>) upper static contact looseness frequency-domain signal; (<b>k</b>) moving contact looseness time-domain signal; (<b>l</b>) moving contact looseness frequency-domain signal; (<b>m</b>) contact erosion time-domain signal; (<b>n</b>) contact erosion frequency-domain signal; (<b>o</b>) contact wear time-domain signal;. (<b>p</b>) contact wear frequency-domain signal.</p> Full article ">Figure 8
<p>SWT time–frequency graphs: (<b>a</b>) normal; (<b>b</b>) jamming; (<b>c</b>) insulated panel looseness; (<b>d</b>) lower static contact looseness; (<b>e</b>) upper static contact looseness; (<b>f</b>) moving contact looseness; (<b>g</b>) contact erosion; (<b>h</b>) contact wear.</p> Full article ">Figure 9
<p>STFT time–frequency graphs: (<b>a</b>) Normal; (<b>b</b>) Jamming; (<b>c</b>) Insulated panel looseness; (<b>d</b>) Lower static contact looseness; (<b>e</b>) Upper static contact looseness; (<b>f</b>) Moving contact looseness; (<b>g</b>) Contact erosion; (<b>h</b>) Contact wear.</p> Full article ">Figure 10
<p>Comparison of different imaging methods.</p> Full article ">Figure 11
<p>Comparison of validation accuracy and loss function for different methods: (<b>a</b>) loss function curve; (<b>b</b>) accuracy curve.</p> Full article ">Figure 12
<p>Time–frequency graphs of OLTC vibration signals under different noise levels: (<b>a</b>) STFT time–frequency graphs without noise; (<b>b</b>) STFT time–frequency graphs with 10 db noise; (<b>c</b>) SWT time–frequency graphs without noise; (<b>d</b>) SWT time–frequency graphs with 10 db noise.</p> Full article ">
Highly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Conferences
Special Issues
Special Issue in
Vibration
Whole-Body Vibration and Hand-Arm Vibration Related to ISO-TC108-SC4 Published Standards
Guest Editors: Setsuo Maeda, Marco TarabiniDeadline: 31 March 2025
Special Issue in
Vibration
Nonlinear Vibration of Mechanical Systems
Guest Editors: Francesco Pellicano, Yuri Mikhlin, Konstantin Avramov, Antonio ZippoDeadline: 15 June 2025
Special Issue in
Vibration
Machine Learning Applications to Vibration Problems
Guest Editor: Maria ChierichettiDeadline: 20 July 2025
Special Issue in
Vibration
Railway Dynamics and Ground-Borne Vibrations
Guest Editors: Aires Colaço, Hassan Liravi, Pedro Alves CostaDeadline: 20 September 2025