Tangotiger Blog

Wednesday, October 02, 2019

Statcast Lab: Cain v Taylor

This is the point at which Cain got the ball.

  ?

Runner is about 75 feet from 3B. Taylor Sprint Speed is 29 ft/s, meaning he needs 75/29 = 2.6 seconds

Cain will have to make an almost 200 foot throw. He has a somewhat below average arm at 85 mph. Here's where we need to leave the world of mph and enter the world of feet / sec. 85mph is 125 ft/s. That's at release. The ball will slow down in flight. Roughly speaking, it'll lose 10% every 60 feet. 

In this case, we'd do 200/60 = 3.33, and 0.9^3.33 = 70%. So at arrival, the speed of the ball is 70% of 125 ft/s or 88 ft/s. So the average speed of the ball in flight is about 106 ft/s. And so, a 200 foot throw will get there in about 200/106 = 1.9 seconds. (It's not this straightforward, but it's close enough.)

The exchange time (pickup to release) for a throw is about 0.5 to 0.75 seconds, which means that the ball would have reached the VICINITY of 3B in 2.4 to 2.65 seconds. It would have been close if the throw was on target. Which of course, it might not be.

How successful would Cain have been? Probably 60% if the throw is on target. And maybe it's on target 70% of the time? So, about 40% of the time he gets the runner maybe?

In the meantime, it would allow the batter to reach second base as the tying run. But, there were two outs! Making the third out at thirdbase is a cardinal sin for baserunners. Which makes it very appealing for the defense.

Let's work some MORE numbers.

http://tangotiger.net/we.html

Bottom of the 8th, 2 outs, down by 2 runs. Our choices are:

• runners on 1B and 3B (our baseline)

or

• runner on 2B and 3B
• end of inning

So, our baseline is a win expectancy for the Nationals of 15.8%.

• If Cain went for it and missed, then the win expectancy is 19.2%.
• If Cain got the out, then the win expectancy for the Nats is 7.1%.

In other words, the tradeoff is that the Nats gets +3.4% if Cain doesn't hit the target in time, or the Nats are -8.7% if Cain gets Taylor to end the inning.

All Cain has to do is make the play 28% of the time. That is:

• 28% of the time, the Nats lose 8.7% 
• 72% of the time, the Nats gain 3.4%

And that's breakeven.

Remember, we guessed that Cain would have gotten Taylor about 40% of the time, and he only needed to get him 30% of the time.

Cain should have gone to third.

Statcast Lab: Park Bias Report in Pitch Speed

?Continuing my look at uncovering park biases, if any, I now turn my attention to Pitch Speed.

The typical way I have done this in the past is the WOWY (with or without you) approach.  It's fairly straightforward, if a bit tricky to code.  You look at pitchers at each park, and compare themselves to their own speeds in the rest-of-league parks.  So, at Fenway and away from Fenway (and not just Redsox pitchers, but ALL pitchers who pitched at Fenway and away from Fenway).  You figure out their difference in speeds, weighted by the lesser of their number of pitches in the "two" parks.  Here's how that looks for 2018 and 2019. (click to embiggen)

?

Now, simply that we get non-zero values doesn't represent a bias.  We have to figure out how much random variation could have contributed to that.  We see in the above that Yankee Stadium appears at the top in both years, while Globe Life Park was up one year and down the other.  This is a good sign that we've got some level of random variation.  A correlation of the two gives us an r of 0.50.  This means that about half of what you see (using this method) is signal and the other half is noise.  So seeing +0.30 in 2019 for Yankee Stadium would mean there is a bias of 0.15 mph.  Every other park in 2019 is less than +/- 0.1 mph.  

This is a very weak bias.  And it's not even clear that this bias would necessarily be at the tracking level. There could be environmental reasons where the release speed is higher in one park or the other.

As I've linked above, and you have seen in my blog the past few months, I have a clearer method to look for park bias: we compare the home pitchers to the away pitchers in the same park.  If for example Citi Field is (literally) home to fireballers, we would not expect the tracking of the away pitchers to also have a high pitch speed.  But, if the Mets pitchers aren't that (pun intended) hot, but the tracking is showing them high, we'd expect the away pitchers to also have their speeds read hot.  

So, a flat line shows zero bias, and a sloped line at 45 degrees shows complete bias.  Here's how it looks in 2018 and 2019, limited to fastballs and sinkers only (click to embiggen):

?

?

To say I was sabermetrically ecstatic when I ran this a few minutes ago is to put it mildly.  Citi Field tracks the home pitchers hot, and the away pitchers not.  Which is what you'd expect on a team of fireballers.  Yankee Stadium does show the away pitchers slightly hot, consistent with the WOWY approach I just presented.

However, we can't just look at individual points.  The key is to look at all 60 points.  And all 60 points are scattered all over the place, with no correlation at all between the fastball speeds of home pitchers to their peers in the same park.

Also note that range in speeds of home pitchers is quite wide, at +/- 1.5 mph, while the away pitchers (made up of basically every other pitcher in the league) at +/- 0.5 mph (or -0.6 to +0.4).

As I do a year-end analysis of all the data points you've seen me post about in the past few years, I will run these home/away park bias reports, so we can see the extent to which biases exist (if any).  And how we need to correct it (as we saw with the Catcher Framing)

Monday, September 23, 2019

Statcast Lab: What impact does Verlander’s historically low BABIP have on our evaluation?

In other words, do we need to worry about DIPS (or FIP)?  No.

Justin Verlander has allowed 487 batted balls, and gotten 349 outs. If we focus only on the quality of contact (launch angle+speed), we'd have expected he gets 345 outs. So, he got only 4 more outs than expected outside of his influence. If you wanted to stop reading here, you'd be fine: Verlander's results are consistent with his individual contributions.

***

What did we not control for? The fielding talent of his fielders, the team alignment of his fielders, and the spray direction of his batted balls. Naturally, all 3 of them are interlinked.

We can focus on the fielding talent of his fielders first. When he was on the mound, his fielders were a little bit above average. How much above average? +4 outs. That is, based on how much distance they had to cover, and how much time they had to get there, the Astros fielders got 4 more outs than average.

In other words, we can explain how he got his 4 extra outs. And therefore, we give Verlander credit for getting 345 outs on 487 batted balls. The league average is 65.5%, and so on 487 batted balls, a league average pitcher would have gotten 319 outs. Since he actually got 345 (after accounting for the talent of his fielders), Verlander is +26 outs.

Now, what about the fielding alignment and spray direction? So, this is an interesting question. The Astros rarely shift on RHH with Verlander pitching, while they always shift on LHH with Verlander pitching. Since Verlander is obviously well aware of the fielding alignment behind him, he is pitching to that alignment. If he can get the hitters to hit to where the fielders are, I'd contend this tells us more about Verlander than the fielders.

Now watch this. With RHH, Verlander got 181 outs, while getting almost 4 outs of support from his fielder's fielding talent. So, that's 177 outs otherwise. And based on quality of contact (speed+angle only), we expected 177 outs.

With LHH, Verlander got 168 outs, with no extra fielding support. Based on quality of contact, we expected 168 outs.

In other words, whether massively shifting all the time, or never shifting, the number of outs that Verlander got is entirely determined by the quality of contact. That is, we can safely ignore the fielding alignment, if we can also ignore the spray direction.

Verlander has a .246 wOBA and a .247 xwOBA. That he happens to have an historically low .218 BABIP is inconsequential.

Statcast Lab: Swing/Take and a Primer on Run Value

Run values of HR

How do we know that a HR will add an average of around 1.4 runs? You can look at it from a pretty high level view and simply look at how many runs a team scores when they hit 0 HR and when they hit 1 HR. When I did this some 15 years ago, the answer was 3.08 runs scored in games with 0 HR and 4.62 runs in games with 1 HR. Taking the huge leap of "all other things equal" (ceteris paribus), that difference of 1.54 runs we would attribute entirely to that 1 HR. In games with 2 HR, there were 6.12 runs score, or 1.50 more runs than the 4.62 runs that scored with 1 HR. So, we attribute that 1.50 runs entirely to that 1 HR.

Now, that huge leap of "all other things equal" can be verified. And indeed, in games where there are no HR, those games also feature a bit less of other hits and walks. In other words, things are not equal. Once we account for that, the end result is closer to 1.4 runs being added by the HR.

RE24

We can get there in other ways. We can look at the 24 base-out states. Bases Empty, 0 outs? That's a base-out state. Runner on 3B, 1 out? That's a base-out state. Runners on the corners, 2 outs? That's a base-out state. There are 8 different combination of base states, and obviously 3 states for the out. And so we have 8 x 3 base-out states. 

Each base-out state has its own run potential. Bases empty 0 outs is about 0.5 runs. That's because in a 4.5 runs per 9 inning environment, you would score 0.5 runs per inning. Meaning that your initial state, the bases empty, 0 outs state, is therefore worth 0.5 runs. What we care about at the START of a state is the POTENTIAL to score, the expectancy. And each of the 24 base-out states has its own run potential, what we call the Run Expectancy chart.

And as you transition from one base-out state to another, that difference we attribute to the event that caused that change. In other words, the event is a causative agent, and we track the change in run expectancy for each event.

A HR with the bases empty 0 outs for example will change the run expectancy from 0.5 runs to 0.5 runs (or a delta of 0 runs), but we added 1 run to the bank. So, the change in run potential + actual runs is exactly 1.0. With bases loaded 2 outs, the starting run expectancy is around 0.8 runs, and the ending run expectancy (bases empty 2 outs, since the HR cleared the bases) is 0.1 runs (plus the 4 runs in the bank). So the change in run expectancy is 4 plus 0.1 minus 0.8 = 3.3 runs. We therefore give 3.3 runs to the HR. 

You go through all 24 base-out states, for every HR that was hit, and you will find that the average change in run expectancy is 1.4 runs. So, the RE24 for a HR is 1.4 runs. We repeat this for all events, and we get the run value of each event, from almost -0.3 runs for an out to +1.4 runs for a HR. 

However, we are going to maintain the run values of each event for each base-out state. We will give credit to a bases loaded 2-out HR far more than a bases empty HR.

RE12

Now, there are also 12 ball-strike (plate count) states. Going from a 0-0 count to a 0-1 count for example decreases the run expectancy by about 0.05 runs. And so we attribute that change in run potential to the strike. A first pitch strike is therefore worth close to 0.05 runs. If this was a 3-2 count, and you get a strike (and hence a strikeout), you would go from around +0.06 runs to -0.27 runs, or a change of -0.33 runs. This I call the RE12 run values.

RE288

We can now MERGE the 24 base-out states with the 12 plate count states (RE24x12 or RE288) to get a run potential for every pitch at every base-out state. A bases empty 0-2 count has a run potential of 0.42 runs. A HR will bring this back to a bases empty 0-0 count (worth 0.51 runs in this chart), along with the HR (1 run), for a difference of 1.09 runs. So an 0-2 HR is worth +1.09 runs.

We can therefore give a run value to every single pitch that we have, over 700,000 such run values. And once we do that, we can aggregate those run values along any dimension we like. Like for example, where in the strike zone the pitch crosses. We created 4 Attack Regions.

Attack Regions

Each of those regions represents something real in baseball. 

• The Heart of the Plate is what the batter is waiting for and the pitcher is avoiding. Pitchers throw about 25% of their pitches here. Batters will generally swing at these pitches almost 75% of the time. And if they don't swing, it's a called strike. 
• The Shadow Zone is the area that straddles the strike zone on both sides: called pitches here are basically 50/50 ball/strikes. Swings generally results in below average results (notably swing and misses). Pitchers are really targetting this region, with over 40% of their pitches coming here, and batters swinging just over 50% of the time.
• The Chase Region is where pitchers are trying to get batters to chase. Almost 25% of their pitches are here, and batters swing almost 25% of those pitches, almost always with poor results. But when they take, it's a called ball.
• The Waste Area are pitches well off the plate, into the batters boxes. Less than 10% of pitches are thrown here, with a bit over 5% of batters still swinging. Virtually no pitcher is actively targetting the Waste Area. And no batter at all ever wants to swing at such a pitch.

We can therefore show the run values for each of these 4 regions, like so.

Swing/Take and more

Furthermore, we can also aggregate the run values along Swing/Take. Alvarez adds 14 runs by swinging 593 times and adds 21 runs by taking 768 times. 

And finally, we can aggregate based on BOTH the Attack Region AND the Swing/Take. Alvarez adds 7 runs by swinging 296 times at pitches in The Shadow Zone.

And you can check it out for any hitter (and pitcher!) right here on Savant.

And for switch-hitters, we also allow you to toggle between LHH and RHH if you so choose, by clicking on the batter image.

What's next? Aggregating by pitch types (fastball, changeup, curve, etc). Or aggregating by plate count. Or aggregating by base-out state. Or by any/all combinations discussed in this blog post. Of course, at some point, you will slice/dice the combinations to such an extent that nothing useful will materialize, so you'll have to be careful. But we're working towards giving you that capability.

In the meantime, you can check out analysis from around the web, like this terrific piece that came up (somehow) minutes after the site became live.

Monday, September 02, 2019

Statcast Lab: How to test for park bias

?About six months ago, in introducing a simple way to create the Catcher Framing metric, I also showed how to quickly test for park bias in that metric.  It actually can apply to any metric.  In any sport.

Let's apply this concept to the exit speed of a batted ball.  The key to the concept is that we presume no relationship in talent between the home batters (and opposing pitchers) compared to the away batters (and home pitchers).  What we do is for each park we figure the average exit speed for the home batters (or the bottom of the inning) and the away batters (or the top of the inning).  In Fenway 2019 for example, the exit speed on the bottom of the inning was 90.7 mph (or +1.9 mph above league average) and in the top of the inning it was -0.1 mph from league average.  We repeat this for all 30 parks, for the five years of Statcast.

If there is no correlation at all, and there shouldn't be based on our assumption of fact, we'll get an r close to 0.  If we do get a larger correlation, that would point to some sort of park bias. That bias could be the tracking system.  It could also be the players responding to the peculiarities of the park.  And what do we get?  r=0.06.  In effect, an r close to 0, and therefore showing no park bias.

Aspiring saberists can use this technique, in any of the sports, to look for biases in metrics, whether measured like I am doing here, or calculated, as I did with the Catcher Framing.

?

Saturday, August 24, 2019

Statcast Lab: do players who radically change their Launch Angle change their Exit Velocity?

?No.

This is what I did.  I looked at all batters in 2018-19 who had at least 100 batted balls in each season.  For each hitter, I tracked the frequency of their launch angle in the sweet spot (8 to 32 degrees, where all the solid hits and HR come), less than 8 degrees (basically GB and very low line drives) and more than 32 degrees (basically high FB or popups).

I classified each hitter based on their change from 2018 and 2019 in the frequency of the above, and dumped them into 5 groups.  The group that lowered their launch angle the most had a drop of an average of -3.5 degrees.  Those that raised the launch angle the most increased by an average of +4.4 degrees.  The other three groups were: -0.8, +0.1, +2.0.

Now, why would we think there might be a change?  Well, it's the mishits.  The top-end exit velocity, we wouldn't expect much to any change.  But the more you deviate your swing plane from the oncoming pitch plane, the less flush you might hit the ball, and so, prone to mishits, which means it'll reduce your exit velocity.  Of course, you are also prone to a complete swing and miss, which will turn a mishit (and its reduced exit velocity) to no-hit, and so removed from the sample!

Anyway, here's the change in exit velocity for our 5 groups:

• +0.3 mph: Lowered Angle (Major)
• -0.1 mph: Lowered Angle (Minor)
• +0.4 mph: Neutral change in Angle
• +0.2 mph: Uppered Angle (Minor)
• +0.5 mph: Uppered Angle (Major)

As you can see, no real trend here.  We do see an overall increase in speed in 2018 to 2019 of about 0.3 mph, which is consistent with a 0.4 mph that I reported earlier.

My next step will be to look if the exit velocity distribution changes by launch angle.  You would THINK that if you lowered your launch angle, then your higher exit velocity will now happen at the lower launch angles.  And similarly, if you increase your launch angle, the higher exit velocity will now happen at the higher launch angles. But, there's reasons to think that it shouldn't matter.  I haven't looked at the data, so as soon as I do, I'll post my findings.

Tuesday, August 20, 2019

Statcast Lab: Refuse the Walk

?A few days ago, some people were talking about approaches on 3-2 counts.  I expanded that to look at any 3-ball count.  And I focused on pitches that were in the Chase Region or Waste Area.  Basically, these are pitches that are automatic walks (you are in a 3-X count, and the pitcher is throwing it well off the plate).  But not all batters will take all the time.  A batter is essentially "refusing" to take the walk at this point.  Here are the "walkaway" rates for hitters who are in a 3-ball count the most often.

There are three things that can happen: 

1. Smartly accepts ball 4
2. Luckily rejects ball 4, by somehow getting a basehit
3. Poorly rejecting ball 4, by whiffing or making an out

That last column, the walkaway rate, is simply the count of poorly-rejected divided by the number of opportunities.

?

(Click to embiggen)

Wednesday, August 07, 2019

Statcast Lab: Barrel Classification - Potential Updates

?I asked Statcast Intern Kristen to review my original classification of Barrels and the other 5 batted ball outcomes.

Here's her report (pdf).  Other than to make one tiny almost inconsequential factual correction, the entirety of the report is hers, and went through no edits on my part.  Based on her findings, in the offseason, we'll need to tweak our definitions.

Friday, July 26, 2019

The ball, the batter, the pitcher, or the fielder?

If a ball is hit 390 feet to dead center, how do we want to handle the CF positioned 300 feet (0% catch prob) from home compared to being positioned 340 feet (100% catch prob) from home.  And how do we want to handle the batter?  Is it a ball hit 390 feet and so is a HR almost 50% of the time?  Or is it a ball that lands 15 feet short of the fence, and so is a HR 0% of the time? And what about the pitcher in all this? Do we care about the ball, the batter, the pitcher, or the fielder?  Or all of them?  Are they intertwined or independent?

Trying to get “one” answer to multiple legitimate questions is how we get into trouble.  If you make the metric so specific that it can ONLY answer one question, you’ve boxed yourself in.

This is why I like FIP: it does what it does, no more, no less.  And it allows other things to be built on top of it.  So in my view, I like speed+angle, because those are the two things the batter has the most influence on.  And it’s “scaled” to hits or wOBA.  “Hit Probability” is too specific a term for what the metric is doing.  We may call it “hit probability”, but it’s more “Speed and Angle impact to hit probability”.  That's the metric.  If we wanted to include EVERYTHING, then guess what: the hit probability is what you see, it was either caught or not.  You have to decide what you want to peel away, and more importantly WHY.

If you follow the FIP approach, what you care about is the influence of the player has on a typical play, not THAT ball, and certainly not THAT play.  There's no right or wrong answer.  You just need to define your question very specifically, and live with the consequences of its implication.  FIP takes a minimalist approach, doesn't try to do too much, and so, is flexible.  That's why speed+angle is what we use for batted balls.

Wednesday, June 19, 2019

How much better is it to have movement on your pitches?

UPDATE: (2019/06/20 10:10)

Following a comment by Saber Watchdog Hareeb, who pointed out a potential bias by temperature (since I did not control for park), I looked into it, and he was totally right.  The bias was noticeable.  As a result, I updated the methodology below to control for temperature and elevation, and excluded Coors altogether.  The text and charts have been updated to reflect the new data. The overall conclusion in terms of direction mostly remains, but the magnitude is reduced in terms of the effect of movement, but not in terms of the effect of runs (overall, but it did have an effect on each pitch type). Thanks Hareeb!

Methodology

Following up on the research method I developed when I looked at speeds of pitches, I am now turning my attention to movement.

Let me give you a brief introduction to that methodology, which has changed ever so slightly:

1. Start with all pitches thrown in 2018
2. Remove all untracked pitches and all knucklers
3. Collapse all pitches into one of these six categories, our Arsenal of Pitches: Risers, Sinkers, Cutters, Changeups, Sliders, Curves
4. Tag every pitch has whether it was low-elevation (under 300 feet) or high-elevation (over 300 feet).  Within each, create three even buckets of Low-, Medium- and High-Temperature.
5. Remove any pitcher that threw fewer than 500 pitches (~30IP)
6. Remove any pitches where a pitcher threw less than 10 pitches of one of the above types
7. Remove all pitches at Coors

What we are left with is therefore: all 464 pitchers in 2018, who threw at least 500 pitches, of which at least 10 were classified as one of riser, sinker, cutter, changeup, slider, curve

Separation

Now we start our separation. We use total inches of movement as our focus. By total inches of movement, I mean the difference in location of the pitch in 2D space at plate crossing, compared to where it would have crossed, if we removed the effect of spin.

For each Arsenal of Pitches (so for example, focusing on Verlander's 816 Sliders) at each Park Grouping (so for example, high-elevation, high-temperature we have 42 Verlander sliders), we break them up into 5 groups based on how much the pitch moved. For the 10% (or 4) pitches that had the most movement, we put them in Group 1. For the 10% pitches that moved the least, we put them in Group 5. For the 40% (17 pitches) that had average movement (for Verlander), we put them in Group 3. We round out Group 2 (20% of pitches, above average movement), and Group 4 (20% of pitches, below average movement).

In other words, we have progressively less movement, as we go from Group 1 to Group 5. And the percentage of pitches in each group follows a 10/20/40/20/10 shape.

This is what it looks like so far. We have 420 of 464 pitchers who threw Risers (4-seam fastballs). Those pitchers averaged 1390 pitches, of which 527 were Risers. They are broken up into 5 groups as shown (the sum of which is 527 pitches).

Movement

Now, how much movement is there from Group 1 to Group 5? Roughly speaking, there's about 1.7 inches of movement between each Group. For Risers and Sinkers, group to group, the difference is about 1.5 inches. While for Curves, the difference is about 2.0 inches group to group. Cutters, Sliders, Changeups are 1.7 to 1.9 inches. Overall, the average is 1.7 inches of difference group to group, or 6.6 inches from high to low groups.

Here's that full chart.

So far, we've selected a large group of pitchers, with a separation by pitch type, and further segmented into amount of movement. The key here, since I did not hit you over the head with it, is that we have proportionate representation of our pitchers. We don't have Verlander's Riser all part of Group 1 and Group 2, even though he throws very hard. No. Only 10% of his Risers are in Group 1. Just like 10% of Jason Vargas "fastballs" are in Group 1. In this way, we are not biasing our data. Proportionate representation. This is the key to this study.

You will notice that we did not control by speed of pitch. Is it possible that the amount of movement is tied in to the speed of the pitch? Sure, it's possible. But we can check. And while theoretically it is possible. In practice, once we group the pitches, there is no bias in pitch speed. This is the other key to the study, but more happenstance, that we are reducing the chance of bias for ancillary reasons. Here's the results of that. Maybe an issue with Cutters, as well as with Curves.

The speed-bias on curves is interesting: the faster it is thrown, the less time in the air, and so, less time for the ball to move. Of course, it's also less time for the batter to react. We're not talking about much of a bias anyway, but we'll deal with that in a future iteration.

Impact by Movement

Anyway, now that we're all happy with where are, now we want to find the IMPACT of movement. To do that, we need a metric. And that metric will be Run Values. A HR has a certain amount of run value (+1.4 runs), a strikeout has a certain amount of run value (around -0.27 runs). Every event has a certain run value. But, we also have non-outcome events, notably balls and strikes. Throwing a strike reduces the potential for future runs, while throwing a ball increases that potential. Generally speaking, it's about +.06 for a ball and -.06 runs for a strike. Basically.

All we have to do now is for every pitch, simply add up the run values based on the event on that pitch (HR, walk, strike, etc). I'll first give you the overall results, then we'll dig deeper for every Arsenal of Pitches. The results are presented in terms of run value per 100 pitches.

Note that a negative number means runs are reduced, the way a lower ERA is better for the pitcher. In other words, negative is good for the pitcher.

The difference between a pitch with the most movement and a pitch with the least movement (ceteris paribus, or all other things equal) is almost 0.80 runs per 100 pitches. You'll remember that the difference in movement from pitches with the most movement to the least movement was 6.6 inches. In other words, each one inch of movement leads to 0.12 runs per 100 pitches of value. And since there's about 150 pitches per 9 IP, that essentially means each one inch of movement will affect your ERA by 0.18.

Arsenal Impact

Now, let's drill down at the Arsenal of Pitches level. Let's start with Risers (4-seam fastballs). Here we see that the change in run value is fairly dramatic. We are comparing 93mph fastballs that move 21 inches to 93mph fastballs that move 15 inches, thrown by the same pitchers in each group. And the run value is -0.46 for fastballs with the most movement to +0.80 runs for fastballs with the least is a dramatic 1.26 runs per 100 pitches of difference. So, fastballs need to move alot. And the more they move, the far more impact they have. 

Sinkers follow a very similar pattern. The effect of Changeups is a bit more muted, with about half the effect, but it follows a similar pattern of Risers and Sinkers.

The effect of Sliders is much more muted. Generally speaking, sliders that move more have more impact. But it's more in terms of a threshold. As you can see in Groups 1, 2, 3, they all have similar run values. A slider needs to move, but it doesn't need too much movement. If we compare Group 3 (-0.59 runs) to Group 5 (-0.27 runs), that's a difference of 0.32 runs (per 100 pitches), compared to a difference of movement of 3.8 inches. That's in the ballpark of 0.08 runs per inch. So, we definitely don't want a non-moving slider.

Curves follow a very similar pattern to Sliders. You want a curve to move, but you don't need too much movement. 

My guess: a curve that moves "too much" is probably a pitch that's going to be way outside the strike zone. In other words, Curve balls are probably going to be thrown to the edge of the strike zone to begin with. Throw them with too much movement, then suddenly, they are way off the plate, and the batter won't be fooled.

A curve that doesn't move enough, essentially a "hanging curve", does have a very notable effect. The difference in run value between Group 3 (-0.19 runs) and Group 5 (+0.34 runs) is 0.53 runs for 4.0 inches of movement. So, this is fairly notable, 0.13 runs per inch.

Cutters are a different story. Their impact does not seem to be tied to their movement. Or if it is, it is not a clean distribution. I would say that Cutters are exception cases, and need special handling.

Conclusion

Overall, I'm quite pleased with the results. The general direction is maintained, that the more movement, the more effective. We learned that some pitches (pitches that tail, meaning Risers, Sinkers, Changeups) are tied heavily to their movement, and pitches that hook (Curves, Sliders) are tied to a minimum level of hook needed. And we learned we need more learning when it comes to Cutters.

Another thing to note is the naming of pitches. This has been an issue for me, that pitchers call their pitches whatever they want to call it, and our policy is to call the pitches what the pitchers call it. So two pitchers can throw the same pitch, at the same speed with the same movement, and one will call it a slider and the other a cutter. Or one will call it a slider, and the other a curve. At some point, I'm going to create my own naming system (without using the words cutter, slider, curve) so as to not conflict with current convention.

Monday, June 17, 2019

Statcast Lab: Creating the Jump Metric

?How do I create a metric, and more specifically, how did the Jump metric come about? There is alot of art and science to the process of metric creation. For the pure artists, sorry, but we need some science. For the pure scientists, sorry, but we need some art.

What I am always trying to do, is organize, classify, categorize the data. We do this so we can actually speak the data. For example, we can create a function of exit speed to create a "hardest hitter". That function would likely be a quadratic function of some sort. Or, we can say "batted ball hit at least 95 mph". As much as the scientists want that function, and as much as I want it as well which you can see it here, it's too hard to speak that. 95+ is ubiquitous. And, just as important, it's an excellent proxy for that function. If we can speak it, with little loss of accuracy, then speak it. In other occasions, I can't do it, and so, I go all-in on creating a function (or series of functions), which is what Catch Probability is. Though even there, I try to come up with a shorthand, such as each foot affects the Catch Probability by 4%.

For Jump specifically, the primary decision is whether to represent the unit in time or distance. Do we want to show that Kiermaier is a certain number of seconds quicker than average, or a certain number of feet quicker than average. And by seconds, I mean, tenths of seconds. As I tried both ways, it become clear, I had to represent it in feet. No one can appreciate what 0.1 or 0.2 seconds means. Everyone can appreciate what 3 feet means. If a player JUST misses a catch, we don't say "he missed it by 0.1 seconds". We DO say "he missed it by a step" (or 3 feet). We can freeze a play and see that distance, but not that time. Anyway, so it become clear that the result had to be in feet.

Once that decision is made, then the other choice is a given: the selection must be made in seconds. In other words, if the unit you create is expressed by time, then the data must be partitioned by distance. And if your unit is expressed in distance, then partition the data by time. This is critical. If you don't see it, you will when you create your own metrics.

Knowing that time is the partition, now we need to select thresholds. We do this because we need to organize, classify, categorize the data. Virtually all catches are made with 3+ seconds from pitch release to catch. This becomes my first point of reference: let's focus on Jump solely based on performance in the first (up to) 3 seconds. It might have been 2 or 2.5 or 2.8. As I tried different ways, 3 seconds became the threshold.

The next thing is what we mean by Jump. And we actually had a few components. After many discussions with the rest of the Statcast team, principally Mike, Jason, Travis, Cory, Matt, we finally settled on three: Reaction, Route, Burst.

It was especially with discussions with Mike that cemented the process. We had a few discussions on whether going "the right way" is needed for Reaction and Burst. Once we decided that Route would encapsulate going "the right way", the other two pieces fell into place quickly.

Burst was interesting because at the same time, Travis was working on speed components for batter-runners, other than Sprint Speed. And since Sprint Speed uses the same scale, and can be compared between batter-runner, runners-on-base, fielders, it was highly desirable, if not necessary, that the same applies for Burst. We quickly settled on 1.5 seconds as the time window for Burst, for batter-runner. And given that I had already established 3 seconds for the Jump window, chopping that into two windows, of 0 to 1.5 (Reaction) and 1.5 to 3.0 (Burst), came into being very quickly. In addition, the Burst Distances for fielders at 1.5 to 3.0 is similar to the Burst Distances for time threshold for batter-runner that we chose. It all came into place.

Reaction was purely distance travelled in the first 1.5 seconds, regardless of direction. Burst was the next 1.5 seconds, also regardless of direction. Route was the bridging metric that was the difference between distance travelled and distance covered. And therefore, Jump is the total distance covered (not travelled) in the first 3 seconds, in the correct direction.

Now, just because all of this came into place and seemed to make sense wasn't enough. We need the metric to actually represent something about the fielder. Once we saw Jackie Bradley Jr being on the leaderboards with both quick reaction and indirect route, year after year, we knew we had it. And then seeing the results of other players, the very strong correlation year to year, it all came into place.

The last step was actually the longest: productionize the metric. We had to get this into the pipeline for our various endpoints. We had to get Daren to add his magic with Savant to take what is essentially tabular data and make it resonate with the fans. Mike had to do all the research to come up with a sabermetric staple of an article, one that is both relevant and timeless.

Anyway, so that's the process for metric creation in general, and for Jump in particular.

Wednesday, May 15, 2019

Statcast Lab: impact of the wall and/or going back on Catch Probability

?One of the team members was asking me how is it possible that the wall and/or going back can have such a dramatic effect on Catch Probability.  And he showed me an example, which was a pretty dramatically different number.  There are four main variables for Catch Probability:

1. How far does the fielder have to run from his starting point to the (eventual) landing point?
2. How much time does he have to get there?
3. Does he need to run back?
4. Is the wall an impediment to making the play?

For this illustration, I will show you the actual results, as well as the estimated catch probability, for plays where the fielder has to run 80 to 90 feet, with an opportunity time (pitch release to landing) of 4.5 to 5.0 seconds, with the 4 combinations of wall and/or back.

??

To read the first line: we have 1101 plays since 2016 where the fielder had to cover 80 to 90 feet in 4.5 to 5.0 seconds, where he did not have to run back, nor was the wall an impediment.  The Estimated Catch Probability was 54%, while the actual catch rate under those conditions was 55%.  The last line shows that the outfielder had to run back and that the wall was an impediment.  Under those conditions, they caught the ball 3% of the time, compared to an estimated 4%.  

I used the above example because that was the test case that I was asked.  The results were pretty good.  Almost as good if I check similar conditions, like so:

??

This one is an extra 0.5 seconds of opportunity time to make the play.  Not nearly as good, but still pretty good.  Also note that those 0.5 seconds adds 30% to 60% of making the out.

The rough rule of thumb is that for plays in the sweetspot, 1 foot = 4% and 0.1 seconds = 10%.  It obviously tapers off when the catch probability is closer to 0% and 100%. 

Below you will find all the data plotted out.

Read More

Wednesday, May 08, 2019

Statcast Outside Lab: Trust the barrels

?There's alot of current and aspiring saberists out there.  You'll usually find them at Fangraphs, like Eli and Craig.  But you'll also find them in their own corner of the blogging world, like Hareeb, who tackles the case of Harrison Bader.  

A couple of days ago, someone noted on Twitter that Bader had a weird combination of LOTS of barrels (which by definition requires at a minimum a high exit velocity) and a LOW AVERAGE exit velocity.  For the two things to be true, Bader would have to have tons of batted balls both at the high and low exit velocity.  Which he does

Back to Hareeb, who then asks which is more indicative of talent, the high barrels or the low exit velocity. I already knew the answer (hint: there's a reason a metric gets created), but I didn't know the extent that it would be true.  He first looks at barrels, avg EV and wOBAcon independently.  He astutely notes:

That’s not a huge win, but it is a win, but since these are three ways of measuring a similar thing (quality of contact), they’re likely to be highly correlated

In other words, he realizes that the correlation is the first step not the last step.  This is why in hockey, NetShots are highly correlated with future NetGoals: part of the NetShots is made up of past NetGoals.  So, both past NetGoals and past NetShots would be correlated to future NetGoals.  The RIGHT thing to do is look at NonGoalShots separate from Goals.  But I digress.

He continues his research with this conclusion:

That’s.. a gigantic effect.  Knowing barrel/contact% provides a HUGE amount of information on top of average exit velocity going forward to the next season. 

...

Knowing barrels on top of average EV tells you a lot.  Knowing average EV on top of barrels tells you a little.

In other words, it's the same spirit as to how I discussed the idea of separating goals and non-goal shots.  He went about it in a clever way, looking at outliers to see the effect. 

Anyway, terrific stuff, the kind of saber work we used to do at the old Baseball Boards (RIP), and we tried to continue ever since.

Monday, April 29, 2019

Statcast Lab: Strike Zone charts

?Just a small thing: if you are interesting in downloading the strike zone charts we are using, they are available here:

 http://tangotiger.net/strikezone/

Artwork by @ee11iott

Saturday, April 20, 2019

How much better is it to throw your fastball at 95mph than 91mph?

?This is what I did: For each pitcher in 2018, I selected all his fastballs (four seamer, two seamer, sinkers), and ordered them from fastest to slowest.  I took each pitcher's 10% fastest pitches and put them in Group 1.  I took each pitcher's 10% slowest pitches and put them in Group 5.  I took each pitcher's next 20% fastest and put them in Group 2, and his next 20% slowest and put them in Group 4.  Finally, his middle 40% pitches by speed are in Group 3.  So, all pitches from Group 1 to Group 5, fastest to slowest.

There were just over 300 pitchers with 500+ fastballs, and that becomes my group of pitchers.  The average speed of each group of pitches follows:

• 95mph: Group 1
• 94mph: Group 2
• 93mph: Group 3
• 92mph: Group 4
• 91mph: Group 5

Oh, one more thing.  For each pitch, I establish a "run value". It's the classic Pete Palmer Linear Weights, but at the pitch level, rather than the plate appearance level.  The more negative the run value, the more runs are suppressed.  Negative is good for pitcher.

So, for each group, I simply figured the average run value, per 100 pitches (roughly a full start).  And the simple average among these 300 pitchers was as follows:

• -0.09 runs: Group 1
• -0.22 runs: Group 2
• -0.10 runs: Group 3
• +0.08 runs: Group 4
• +0.38 runs: Group 5

Now, this is very interesting.  While throwing faster does in fact get better results, it's not totally dispositive.  It is possible that at the very highest speed, the pitcher is losing... something.  Maybe control? I'll have to do a breakdown.  (Or better yet, the aspiring saberist out there can do that.) Otherwise, for the other groups of speed (Groups 2 through 5), there's a 0.1 to 0.3 runs of gain, per 100 pitches, per 1 mph.  

In terms of per 9 IP, you can multiply all that by 1.5. So, Group 5 to Group 4 is an improvement of about 0.45 runs per 9IP for that one extra mph.  From Group 4 to Group 3, it's 0.27 runs per 9IP.  From Group 3 to Group 2, it's 0.18 runs per 9IP.  From Group 2 to Group 1, it goes the other way.

So, it depends how you want to look at it.  If you look at Group 5 to Group 1, that's 4 extra mph, and an improvement of 0.47 runs per 100 pitches, or 0.70 runs per 9IP, or about 0.18 runs per 9IP per mph.  If you look at it from Group 4 to Group 2, that's 2 extra mph and an improvement of 0.30 runs per 100 pitches, or 0.45 runs per 9IP, or about 0.22 runs per 9IP.

Therefore, I think we can safely say that it's about 0.20 runs per 9IP per mph.

***

What is interesting about this is that this is consistent with findings from a decade ago.  In the Rule of 17, pitchers as starting pitchers give up 17% more runs than those same pitchers would give up as relievers.  Which roughly translates to about 0.70 runs.  And those pitchers, as relievers will throw 3 or 4 mph faster than as starters.

***

In the comments, I'll take a look at the other pitches in the arsenal to see if this effect applies to them as well.  Stay tuned.

Sunday, March 24, 2019

WOWY Framing, part 2 of N: with or without Bartolo

In 2018, Bartolo Colon threw 500 pitches in The Shadow Zone.  Among the 156 pitchers with at least 300 such pitches, his 56.8% called strike rate was fourth highest.  The range was 58.3% down to 35.9%, with a mean of 47.3%.  

The Shadow Zone is the region between the Heart of the Plate (the region where batters want to see pitches, and so virtually every take is called a strike) and the Chase Zone (the region where the pitchers are hoping the batters chase pitches, and so virtually every take is called a ball).  That Shadow Zone nestled between the two is pretty wide, straddling both sides along the edge of the strike zone.

As a result, we can further subdivide The Shadow Zone into Inner Shadow Zone (meaning the part of the Shadow Zone that is part of the textbook strike zone), and the Outer Shadow Zone (or the part just outside the strike zone).  When we do that, we see that Bartolo gets 83% called strike rate in the Inner Shadow and 30% in the Outer Shadow.  The league average is 79% and 22% respectively.  That puts Bartolo above average in both regions.

As we know, the catcher plays a role in getting the called strikes.  Bartolo had three catchers last year.  This is how many pitches he threw to each of them in the Inner Shadow, and how often he got the called strike rate:

• 0.832 (203) Chirinos, Robinson
• 0.795 (44) Perez, Carlos
• 0.857 (7) Kiner-Falefa, Isiah

With each of them, he got above average called strikes.  Is this about Bartolo?  Or, did Bartolo happen to have three catchers each of them above average?

Welcome to WOWY, With or Without You.  Chirinos faced 29 (!) different pitchers.  The one he paired with the most was Bartolo, which means he had 28 pitchers without Bartolo.  From Cole Hamels and his 145 pitches in the Inner Shadow down to Zac Curtis and his 1 pitch.  Without Bartolo on the mound, these 28 pitchers threw 1277 pitches in the Inner Shadow.  Their called strike rate was 73%.  Since we can take a reasonably small step to call these 28 pitchers "average", we can therefore compare Bartolo to these 28 pitchers through the "common catcher", and say that Bartolo is +10% in terms of getting the called strike rate.

We can repeat this exercise with his other two catchers.  Kiner-Falefa got 72% called strike rate without Bartolo and Perez got 73% called strike rate without Bartolo.

So, adding everything up, and his catchers, without Bartolo, caught 1959 pitches in the Inner Shadow from 40 other pitchers, of which 73% were called strikes.

By going through this process, we can establish how much of an effect each pitcher has on each catcher.  Bartolo therefore is about +10% in the Inner Shadow.

There are two other things I haven't mentioned.  One is the park.  But in this particular case, Bartolo threw in about the same parks as his peers (the other pitchers of his catchers), so that's not really an issue.

The other is Random Variation.  Because as much as we have OBSERVED Bartolo to be +10% on 254 pitches in the Inner Shadow, it is still only 254 and so subject to Random Variation.  When we remove the effect of that, it cuts his impact by about half. And so I credit him with +5%.

When we repeat for the Outer Shadow, his 30% called strike rate is compared to his peers (through the common-catchers) of 19%.  That's +11%, which I cut down in half in his case to 5.5%.

And therein lies the problem.  By treating them independently, I'm not taking advantage of the fact that each region can inform on the other.  And so, I really do not want to cut each one in half.  It'll probably be 30%.  But let's talk about that next time.

Saturday, March 23, 2019

WOWY Framing, part 1 of N

Rewind

About 15 years ago, I introduced a concept I subsequently called WOWY (With Or Without You). The idea has its roots to the way the NHL originally introduced plus/minus. Back then, they compared a player's plus as a percentage of all goals scored by his team in his games, and similarly for the minus. My slight adjustment to what the NHL used to do was to compare a player's plus/minus to that of his team without him on the ice. So, team performance with the player, compared to team performance without the player. The difference, after accounting for Random Variation (and other systematic biases), we'd attribute to the player himself.

You can see what I did with pitchers, with and without their catchers. I did it for the baserunning stats (SB, CS, WP, PB, BK, PK). Strangely, I noted this as an afterthought, and never followed up:

I'm not including blocking the plate or framing the pitches, though that last part might be doable (though I'd have to look at the pitcher's age as well; I'm guessing that the above numbers aren't too dependent on the pitcher's age, which may or may not be a good guess.)

I clearly should have taken the next step and simply tried it with walks and strikeouts. And given the results we have all seen on catcher framing at the pitch level, it's likely we WILL find something notable here, using only walks and strikeouts. Enough that we'll be able to do framing across the Retrosheet years. That's the hope anyway. I'll get to it this year.

Now

For now, I'll turn my attention to WOWY Framing, using pitch locations. I'm going to show how simple and straightforward the process is. And then I'll make it A BIT more complex. And maybe in the future, we'll continue to make it a bit more complex that that. There is an R package that helps this process along greatly, and once I can code an R program without an error, I'll finally do that. Until then, we'll SQL our way through this.

The first step, before we even identify the major variables, is to create a baseline. There's no point to dive in and start figuring out all the variables, if you don't know what your starting point is. And at its most basic, framing is simply about getting called strikes at pitches at the edge of the strike zone. Yes, there is more to it than that. That's how you scare away researchers. "Yeah, but..." Let's not scare them away yet. There's plenty of time for that. For now, let's just bring everyone on board.

A few months back, I showed how often each catcher caught a strike, in what we call The Shadow Zone, which is the region that borders the strike zone.

The average called strike rate in this region is around 47 or 48%, with a range of about +/- 5 or 6%. Jeff Mathis had 55% called strikes on 1726 pitches, where the NOMINAL average is 47%. In other words, if this nominal average is the TRUE average, he's getting 0.08 more strikes per pitch in the Shadow Zone. Which when we multiply by his 1726 pitches gets us 130 more called strikes. On the bottom end is Mitch Garver with 127 fewer called strikes, in the "same" Shadow Zone.

Now, it's not EXACTLY the same Shadow Zone, and we'll get to that in a sec.

Mountains and Pools

My buddies at @SteamerPro and @Fangraphs released their Framing numbers, which is about 4 levels higher than what I've just done. Their version is essentially Mount Everest. Which gives us a chance to compare how close we are with our base version. Is our base version at sea level, or is our base version at Base Camp?

That's a correlation of r=0.88. This means that simply using the called strike rates in The Shadow Zone, without any kind of adjustment whatsoever, we're already at Base Camp. 

This becomes an important point here. If we are going to show the catcher framing numbers, with all its (necessary) adjustments, we should AT LEAST show the called strike rates in The Shadow Zone. This is akin to needing to show ERA *and* ERA-. We can't just show Freeland's ERA- of 61, between Nola at 59 and Scherzer at 62. We really need to show their ERA as well (2.85, 2.37, 2.53 respectively). While we undoubtedly need to adjust for parks, and for Coors especially, we also need to show that Freeland's ERA- is LARGELY a product of just plain ole ERA; the park adjustment, while real, is not causing an ERA of 4.56 to be considered equal to Nola and Scherzer.

So, just as a matter of form and suggestion, it would behoove Fangraphs and the other Catcher Framing providers to ALSO show the baseline. Furthermore, it would allow us to talk about this in REAL terms. Mathis caught 55% called strikes on the edges of the strike zone to lead the league. That, by itself, is enough of a talking point. It gets everyone into the wading pool. We can go deeper if we need to, and eventually go to the deep end of the pool for all the adjustments. But, baby steps first. Let's start with splashing our feet.

Shallow Now

Having introduced you to the wading pool, let's now go to the shallow end. We can do a WOWY that will control for the venue, on the idea that the tracking mechanisms of each park is not identical. And so, when we see a 47% called strike rate, it might be slightly different at each park. The park in SF had a 48.9% called strike rate. And when we isolate all the pitcher-catchers who pitched with or against the Giants, and then took those pitcher-catchers at the other 29 ballparks, we see that THOSE battery mates had a 46.6% called strike rate. In other words, we OBSERVE a 2.3% difference. Which we need to regress, since some of that is just Random Variation. And I estimate that true difference to be 1.46%. On the other end is Global Life Park at -1.67%. Coors Field is next at -1.47%, and we'll talk about them with Iannetta soon.

Having established the effect of each park, we can now do our pitcher-catcher WOWY, and adjust out the venues. And when we do that, we end up with the leaders and trailers of Bartolo Colon (hi Julia!), and James Paxton (hi Ellen!).

Paxton had 42% called strike rate in The Shadow Zone, against an expectation of 51%, given his catchers, and adjusting for the venue. That's a 9% shortfall, of which our TRUE estimate is about 6%.

Colon had 57% of his pitches called strike in The Shadow Zone, against an expectation of 43%, or 14% higher, of which our true estimate is about 9%. Note that we haven't even talked about the PARTS of The Shadow Zone, or the pitch trajectory (and Colon being a notoriously fastball-first and essentially fastball-mostly pitcher, could very well have a much higher expectation than the 43% we are seeing).

Anyway, having now determined adjustment factors for venues and pitchers we can now go back and look at each of our catchers Base Camp numbers, or wading pool numbers, and bring them into the shallow end. And when we do that we get this at the top and bottom end (converting each extra called strike at 0.12 runs per pitch):

?

• strike_shadow is the wading pool number
• adj_strike_shadow applies basic adjustment for venue and pitcher (Mathis had favorable context here)
• runs1 converts the extra basic strikes called into runs with a basic 0.12 runs per pitch multiplier
• runs2 uses the adjusted numbers
• Steamer is our Deep End number (thanks to Jared)

As you can see, not much of an adjustment. The correlation does get us a bit closer to Steamer's Deep End numbers (we are now at r=0.89).

Tomorrow

Tomorrow, I'll take the next step, and break up The Shadow Zone into two zones: the part that is inside the strike zone, and the part that is outside the strike zone. Just to whet your appetite, the called strike rate on the inner part of The Shadow Zone is 79% and in the outer part it is 22%. In other words, maybe we'll find pitchers like Bartolo might throw more pitches in the inner part of The Shadow Zone and so that 57% of his we see might be a product of that. Or not. I don't know, since I haven't checked. And I'm going to bed now. See you tomorrow.

Thursday, March 07, 2019

Statcast Lab: App for Pitcher Similarity Scores (pitch level)

This is a cool app we rolled out at Savant.  It is a pitch-level similarity.

The way it works is as follows.  Start with one game, say deGrom's first start.  We look at each pitch in deGrom's first start, based on the speed and movement.  Then we simply ask: of the other 700,000 pitches thrown in the league, which pitches looked like this one.  Then, we total up for each game how many of these pitches looked like deGrom's first start.  If a pitcher had a start that looked like it could be deGrom's, that's a match. Then we repeat with deGrom's 2nd and 3rd and all his starts, always asking the same question. And we repeat this for all pitchers.  (At the moment, it's limited to pitchers with at least 12 games of more than 60 pitches.)

What is fascinating with this approach is that it self-validates: the pitcher whose games look the most like deGrom's first start is all the other games thrown by deGrom.  And this is true of every single pitcher.  The fun is which other pitchers have similar games in terms of speed and movement.

Scherzer is interesting because when we limit ourselves to speed and movement, he doesn't really stand out.  So, there's more to being similar than just the speed and movement of pitches.  So, be careful how far you take this.

The app is fun on its own.  Click and drag all over the place.  The pitch types follow the standard Statcast color scheme.  The app itself was designed by Statcast Viz Jock @ee11iott.

***

Note: we'll also be rolling out a sim score app based on OUTCOMES, so, strikeouts, walks, barrels, topped balls, etc.  That one will comport more to the way you might think of similarity scores.  And this particular app will be for both batters and pitchers.

Tuesday, March 05, 2019

Statcast Lab: xDistance

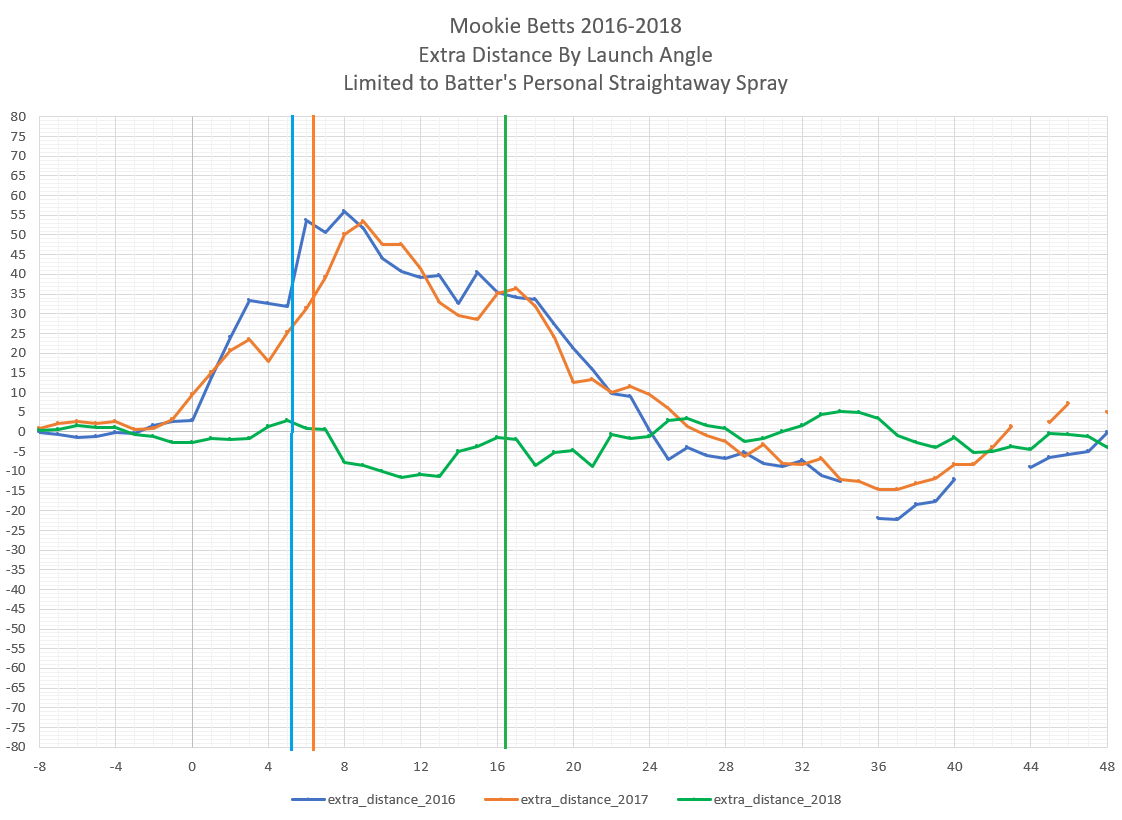
Focus on a hitter's hardest hit balls. Those are likely those that he got all of it, and so likely what he intended to do.  The launch angle that resulted is probably what he's after.  For Mookie Betts in 2016-2017, that launch angle was at 5 degrees (blue vertical below) and 6 degrees (orange vertical line below).  In 2018, it was very different at 16 degrees (green vertical line below).

Focusing on a hitter's hardest hit balls also gives us his intended spray direction.  We can take all the batted balls at +/- 10 degrees of his intended spray direction to give us his personal straightaway spray direction.  Interestingly, in 2016, that was -8 degrees, which is about typical for an MLB hitter, targetting a spot halfway between the shortstop and the 2b bag. In 2017 he pulled more, at -13 degrees, so targetting more directly toward the SS, or the gap between LF and CF.  And in 2018, he did the same at -13 degrees.  If we focus on these batted balls, balls that he hit at his presumed straightaway, we get the distance of each batted ball.

We can then determine what the distance hit for his actual speed+angle by the league, what we can call his xDistance.  And then simply compare his actual distance to the xDistance, for the Extra Distance.  That's what the chart below is showing.  And we can see that in 2016-17, at the line drive angles, meaning 4-20 degrees, Betts was getting plenty of Extra Distance.  Which if you are hitting slightly under is what you would get.  In 2018, he must have retooled his swing, since he did not get extra distance on his line drive angles.  Indeed, he was short a bit.

But it's not all about the distance.  What you care about as well is the frequency of hitting balls in the sweet spot launch angles of 8-32 (and hopefully hitting it hard at those angles).  And Betts was among the league leaders in both Hard Hit % and Sweet Spot Angle % (11th and 27th respectively).  New teammate JD Martinez was 4th and 20th respectively.

?

Sunday, February 24, 2019

Statcast Lab: Active Spin Percentage

Knucklers, football

A knuckleball will move in haphazard ways with almost no spin. You can thank the seams of the baseball for that. Otherwise, a spinless smooth ball will not move beyond its straight line trajectory other than for gravity.

A perfect spiral football will also not move left or right. You can thank the axis being pointed along its direction. What is the axis of a football? First, remember that a ball spins around its axis. And we are all familiar with how a football spins. If you hold a football, your thumb will be pointed toward you, near the back tip of the football. So, the axis of the football is aligned with the direction the football is going in, which is exactly opposite to where your thumb is pointing. Thumb points toward you, football goes exactly in the opposite direction. And so, such a football has no left/right movement.

Fastball, curveball

A pure fastball is thrown with your thumb (i.e., the axis of a baseball) perpendicular to the direction of motion. Your fingers point in the direction of motion, while your thumb points exactly opposite to the spin axis.

The backspin of the ball is counteracting part of the effect of gravity, and so will end up higher than it otherwise would be without backspin. That's an upward deflection. A curveball is thrown with topspin, adding to gravity with additional downward deflection. When thrown with pure top or backspin, then the entire movement of these deflections can be estimated based on the number of revolutions the ball makes toward the plate. In other words, 100% of the spin contributes to movement. We call the spin that contributes to movement as Active Spin. You can also throw a pitch with some side-action so that some of the deflection will go up or down, and some will go side to side. All of this is Active Spin.

Interlude: In other literature, you will see terms like "useful spin" or "spin efficiency". In my view, these are not the best terms. The opposite of useful is useless, and a pitch with not high spin efficiency will have low efficiency. Both these terms would imply, to a lay user, that useless spin and low efficiency is bad. By instead using the term Active Spin, the opposite of Active is Inactive. Neither word implies anything good or bad. Hence, Active Spin provides a meaningful word without being ambiguous.

How do you get Inactive Spin? That's a football. For a football, none of the spin contributes to movement, and so, a football has 100% Inactive Spin. In order for a baseball to have Inactive Spin, you would twist your arm slightly so that the baseball is thrown more like a football. The more the baseball is thrown like a football, the more the spin of a baseball will go from Active Spin to Inactive Spin.

Active Spin Percentage

The technology currently used in MLB parks and elsewhere to track the trajectory of the pitch also measures the spin rate--or RPM--of the pitch, which allows us to easily convert that into number of revolutions in its flight. We can also infer the amount of movement of a ball based on its estimated trajectory of measured points along that trajectory.

Alan Nathan was generous enough to provide the physics-based math equations that allow us to estimate how much movement we'd expect for each pitch based mostly on the amount of spin. By comparing the calculated movement to the estimated max-movement, we end up with an estimated Active Spin Percentage: the percentage of a pitch's spin that contributes to movement. In other words, a pitch that is 100% Active Spin is thrown with pure backspin or pure topspin, or any spin as long as the axis (your thumb) is perpendicular to the direction of motion. And a pitch that is 0% Active Spin is essentially thrown like a football, with your thumb parallel to the direction of motion.

Sample players

Verlander throws his fastball with essentially 100% Active Spin. When we calculate it pitch by pitch, we get a range of around 85 to 115%, which is what happens when we compare estimated values with inferred values. So, there's a margin of error we have to appreciate, of which most of it goes away when we are talking about 1000+ pitches.

Interlude: if one SD (standard deviation) is say about 5% of error, then if you have 100 pitches, it chops that down to 0.5%. That's because you can reduce the amount of error by the square root of the number of pitches: square root of 100 is 10, so divide 5% by 10, and you get 0.5%. Similarly, if you have 2500 pitches (of which the square root is 50), it chops it down to 0.1% (5 divided by 50).

Patrick Corbin for example throws his excellent slider with 22% of Active Spin. Is that good or bad? Given that he might have the best slider in MLB, it's good. Would 24% or 20% be better? I don't know. It's likely that 22% is perfect. When you are the best at something, then you've probably figure it out.

Interestingly, we have his curveball at 17%, which is a FAR CRY from almost all other curveballs. Garrett Richards for example is at 97%. It's an almost certainty that Corbin is throwing a "slow" slider, and not a curveball. But in the world of nomenclature, we live with what we've got. The reality is that, analytically, you can't include Corbin's 73mph "curve" with Richards' 81mph curve or Wainwright's 73mph curve.

?

A special thanks to Alan Nathan for a review of this post. Anything that the reader disagrees with, he is disagreeing with me.