Tangotiger Blog

Monday, October 19, 2020

Statcast Lab: How much space should you place between infielders, part 2 of N

This blog post is focused on RHH, with three infielders on the left side. Part 1 is here.

The wOBA is .354, which is 25 points higher than the .329 when you have two infielders on the left side. This is extremely high, and calls into question the entire concept of putting three infielders to the left side against a RHH. But is there some combination where we can put three infielders to the left side successfully?

First some spatial breakdowns.

Thirdbase:

• Small gap: less than 6 degrees from the 3B line
• Normal gap: 6 to 8 degrees from the 3B line
• Large gap: more than 8 degrees from the 3B line

Shortstop:

• Small gap: less than 14 degrees from the thirdbase (player)
• Normal gap: 14 to 16 degrees from the thirdbase
• Large gap: more than 16 degrees from the thirdbase

Secondbase:

• Small gap: less than 16 degrees from the shortstop
• Normal gap: 16 to 18 degrees from the shortstop
• Large gap: more than 18 degrees from the shortstop

Now, is there a combination where we get even league-average results (.329 wOBA)? Of the 27 combinations, there are 4 combinations that we have better than league average results. The sample size however is small to the point that it’s not even one standard deviation from the mean. But, we’re looking for any little win here.

Best Combos

The thirdbase is playing close to the line, the shortstop is playing close to the 3B, and the 2B is 8 degrees from the bag. With only 54 attempts, that wOBA was .272.

The next best combo (61 attempts, .289 wOBA): third base close to the line, the shortstop normally spaced from thirdbase, and the secondbase closer to the shortstop (10 degrees from the bag). In other words, if you shift the 3B over, make sure to get that 2B shifted over as well.

The third best combo (193 attempts, .308 wOBA): third base in a normal spot, the shortstop with extra spacing from thirdbase, and the secondbase closer to the shortstop. Now, I should remind you when I say “normal spot” I mean in terms of having three infielders to one side.

The last good combo (44 attempts, .290 wOBA): third base close to the line, the shorstop close to the thirdbase, and secondbase in a normal spacing from shortstop.

That’s it, nothing else good. As for the bad combos, there’s a bunch of them.

Worst Combos

The sixth worst is the “normal” spacing for each fielder. It’s obviously the most common, and the wOBA was .343.

The worst has the 3B and SS in the normal spot, and the secondbase closer to the bag. In other words: they went to the risk of putting three infielders to one side, but (they thought they) hedged their bets by keeping the secondbase close to the bag. That is actually the worst thing they can do. The wOBA was .372 on 968 attempts.

The next worst had the 3B away from the line, the SS staying close to the 3B, and 2B normally spaced from SS. That’s a wOBA of .394 (worse than above) but only 300 attempts. In terms of z-score, terrible but not as terrible as above.

The third worst: .370 wOBA with the 3B and SS in their normal spot and the 2B too close to the SS.

The fourth worst: .397 wOBA (highest of all, but only 236 attempts): 3B close to the line, SS wider spaced from 3B, 2B normally spaced from SS.

Overall

If you are going to put three infielders to one side, you have to move that 3B close to the line. Three infielders means you are playing to pull, so you need to close the gap to the line. Don’t put too much space between the 3B and SS. The 2B is a bit harder to pin down, but he has to be off the 2B bag to a good, but not great degree.  Specifically, we get a .310 wOBA on 371 opportunities when you have this fielding alignment: 3B at -40 degrees, SS at -26 degrees, 2B at -8 degrees.  More broadly: 3B has to be within 5 degrees of the line, the SS within 15 degrees of 3B and the 2B 15-20 degrees from the SS.  That's your best bet to getting a winning spatial-based alignment against RHH with three infielders.

But if you really have to do something: don’t put three infielders to the left side against a RHH so often. Or even maybe ever.

Statcast Lab: How much space should you place between infielders, part 1 of N

This blog post is focused on RHH, with two infielders to either side of the bag.

I looked at the fielding position of all thirdbase relative to the 3B line, and broke them up into three groups:

• Small gap: less than 7 degrees from the 3B line
• Normal gap: 7 to 10 degrees from the 3B line
• Large gap: more than 10 degrees from the 3B line

I did similarly for the shortstop:

• Small gap: less than 16 degrees from the thirdbase (player)
• Normal gap: 16 to 21 degrees from the thirdbase
• Large gap: more than 21 degrees from the thirdbase

And for the secondbase:

• Small gap: less than 23 degrees from the shortstop
• Normal gap: 23 to 28 degrees from the shortstop
• Large gap: more than 28 degrees from the shortstop

That gives us 27 possible combinations of spatially-based alignments. There actually was one combination that was never tried: 3B close to the line, the SS close to the 3B and the 2B close to the SS. But that’s a technicality, as to make that happen, it’s just about impossible with only two fielders on the left-side. So, we have really 26 possible combinations. Three combinations were tried less than 20 times across the league, so we are now down to 23 possible combinations.

The league average wOBA was .329 (I include errors as singles). The most popular combination was the Normal/Normal/Normal gap. The league wOBA was .335. It was also the third highest wOBA of the 23 possible combinations. A simple rule is: do something that’s not normal. Of course, you can’t be too abnormal.

Worst combos

The worst combination yielded a wOBA of .383 (54 points higher than league average). That one was based on the thirdbase being close to the line, the SS at a normal gap from the 3B, and the 2B at a large gap from the SS. In other words, both the 3B and SS shifted over by about three degrees, while the 2B didn’t move. That opened up the gap between SS and 2B too much. Result: highest wOBA and worst spatially-based fielding alignment.

The second worst combination: .362 wOBA (33 points higher than league average). In this case, the 3B and 2B played in their normal spot, but the SS was playing closer to the 3B. In other words: the gap between SS and 2B was too wide.

The third worst combination was everyone playing their normal spot.

The fourth worst combination, albeit at a wOBA of .337, was the 3B and SS in their normal spot, and the 2B shifted over to the right side. In other words: the gap between SS and 2B too wide. So at this point, we learned our lesson: don’t open up that spot between SS and 2B.

Best combos

Let’s now look at the best combinations. A very low .302 wOBA (27 points lower than league average). How did that happen? Open up the gap between 3B and SS. In other words, the “normal” SS spot needs to have a new normal, and they need to be moved away from 3B and toward 2B. This is consistent with what we just learned about the Worst Combos.

The second best combination: .309 wOBA (20 points better than league average). This one had the 3B farther from the line, while the SS and 2B shifted over as well. In other words, don’t play to pull so much.

The third best combination: .313 wOBA (16 points better than league average). This one had the 3B and SS in their normal spots, but the 2B was closer to the bag. In other words, close some of that gap between SS and 2B.

Other combos

There were other combos that showed positive results for the defense, but the sample size was a bit low. We can however try to combine some of those combinations to come up with additional rules.

• When the 3B plays close to the line, make sure you don’t shift the SS closer too much to compensate, and definitely don’t allow the gap between SS and 2B to get larger. If you follow that rule, then you end up with 20 points better than league average.

Next up, we’ll look at what happens when you put three infielders to the left side against RHH. Those who have followed my blog over the years know that this is a risky thing to do. But maybe there’s some combination that lets us get something positive out of it. Stay tuned…

Sunday, August 09, 2020

DER and BABIP tweetstorm

This was a tweetstorm from a few days ago.

***

Since start of 2020 season, fielders have converted into outs 71.1% of the 7630 balls of hit into play

In 2019, there was NO STRETCH where fielders converted as many plays into outs. The average was 69.1%

2020 is 3.8 standard deviations from 2019

DER is essentially 1 - BABIP

***

We are talking 2019 to 2020. I don’t know what level of talent influx you can have in the offseason that is targetted to fielding.

Fielding alignment might be one reason.

***

It’s not just a 2019-20 difference. This is consistent back to 2016 (and earlier).

HR rates are no different in 2020 than in 2016-19:

***

Those that have “angle” in it is using tracked data. The remaining (editor’s note: which is very very limited in 2020) is using stringer data. The tracked and untracked data will be biased, so be careful in making too strong a conclusion.

***

From 2010-2019, the DER for SP was .691, the same as for RP.

In 2020:
.718 SP
.703 RP

So, Starting Pitchers are driving the big change

***

This shows how often balls assigned to outfielders are converted into outs.

It removes balls assigned to infielders as well as any "impossible to make" plays.  As you can see, a slightly more number of plays being made by outfielders meaning slightly better positioning, or balls luckily getting closer to the outfielders.  This is only one standard deviation, so, not THAT much of an impact. And since it's a different tracking software, it could be slightly different as a result.

So, probably not due to OF positioning.

Saturday, August 08, 2020

Does Successful Shifters Keep Shifting?

Executive Summary:

No, they increased their shifting as much as any other group.  And they did not get any more additional benefit out of it.

Study:

This study, Do Successful Launch Anglers keep Angling? (yes!) is one of my favorites. The framework is simple enough. And since I liked it, and it’s simple enough, I reused it for the next study: Do Successful Zoners keep Zoning? (no!).

I will continue its use for this new study in the trilogy: Does Successful Shifters Keep Shifting?

As we know, Shifting is everywhere.  From 2017 to today, shifting has gone in a smooth progression from 12% to 35%.  This is fantastic for researchers, since we always look for these kinds of changes.  BABIP (number of hits per ball in play) however has held steady from 1993-2019, from .290 to .299.  In the "shift era", it's been at .293 to .298.  In other words, for all its radical change in usage, we don't see evidence of a change in outcomes.  

So this year, BABIP is down to pre-1993 levels at .276. From 1973 to 1992, BABIP has held steady from .274 to .285.  And people are tempted to pair that enormous drop to the new jump in shifting.  But the jump in shifting between 2019 and 2020 is similar to that of 2018 to 2019.  You can't claim jump in shifting results in better production from 2019-2020 and turn a blind eye to the lack of change in production in 2018-2019.

As fascinating as the change in BABIP is (you can see my tweetstorm for that), let's focus on the question at hand: Does Successful Shifters Keep Shifting?

I will be looking at the change in wOBA and the change in shifts to see if there's a relationship there.  Doing it the simple way, and we see no relationship at all.

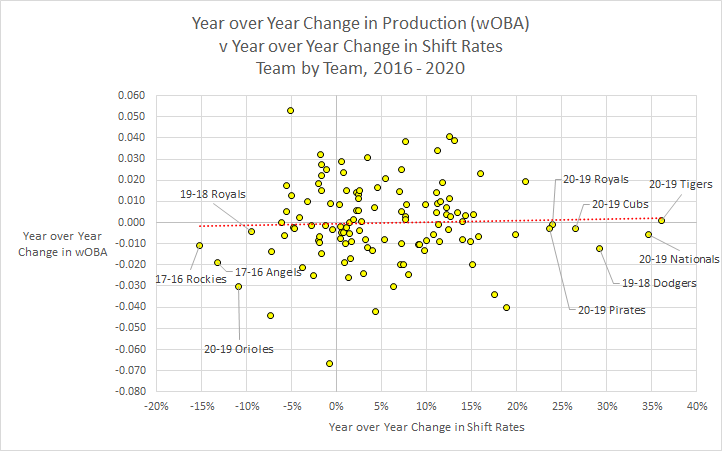
But let's do it as part of the trilogy framework.  We look at each team year-to-year since 2016.  This will give us 90 teams.  (30 for 2016-17, 30 for 2017-18, 30 for 2018-19).  Of those, we split them up into three groups based on their overall change in production, using wOBA (relative to league).

For the 28 teams that improved their wOBA the most, they dropped their wOBA by 16 points.

For the 28 teams that got their worst wOBA change, they increased their wOBA by 16 points.

The middle 34 teams had a 1 point drop in wOBA.

In the year AFTER that (so for the 2016-17 teams, we look at their 2018 production), the 28 most successful teams further dropped their wOBA... but by 1 point.  The 28 least successful teams remained flat.  The middle 34 teams had a 1 point increase.

In other words, once you look beyond the observation window, and look at the data that is unbiased, we find no evidence of anything continuing.  That is, there's no "momentum" to the change in performance.  If you got better or worse year to year, the result of the year after that window is league average.

But what about the change in shifting?  Well those teams that had the biggest drop in wOBA increased their shifting rate (7%) by about the same amount that those whose wOBA got worse (+5% increase in shifting). The middle teams increased shifting by 8%.  In other words, we can't pair change in production to any future change in shifting patterns.

Now, is this true for the teams that increased or decreased their amount of shifting?  This is where the rest of the trilogy framework comes in.

The Most Successful Teams

So, let's go back to the 28 most successful teams in improving their wOBA year to year and ask this question: what was their wOBA in the year after the window, if we break it down by their change in shifting approach?

For those 28 that most improved their performance, we have this breakdown:

7 teams paired that, while decreasing shifting year to year (-6% points)

12 paired that while slightly increasing shifting (+4% points)

9 paired that while massively increasing shifting (+14% points)

That's our year to year window.  What happened to these teams in the year AFTER the window?  All increased shifting at about the same rate (5% to 8%).  In terms of production, it's a bit of a jumble.  The teams that in the window reduced shifting, ended up with an increase in wOBA of 7 points, while the teams that increased shifting ended up with a further drop in wOBA of 2 points.  The teams that were in-between had the best improvement at 6 points.

In other words, for these 28 teams that had the most success in the window, that success had a small relationship to continued success based on "more shifting is good".

The Least Successful Teams

What about the 28 teams whose production dropped the most in the year to year window?  We have this breakdown:

9 teams paired that, while decreasing shifting year to year (-3% points)

12 paired that while slightly increasing shifting (+3% points)

7 paired that while massively increasing shifting (+13% points)

So we have three very different mindsets.  Did the mindset of those teams portend anything?  In this case, it was a reverse from the most successful teams.  The 9 teams that had the biggest increase in wOBA while pairing that with a decreasing number of shifts, had in the year after this window... no change in wOBA.  

The 7 teams with the biggest increase in wOBA while also massively increasing shifting, had in the year after this window continued their jump in shifting (aka, doubled-down) and... further increased their wOBA by 5 points.

Summary

So what did we learn?  We can't really focus on NUMBER of shifts.  It's very (very very) possible that teams are overdoing the shifting, that they are shifting too indiscriminately.  This is almost certainly the case against RHH.  

In one respect, this is much like the Launch Angle Revolution.  It's not "higher is better".  That's because there's an optimum range for launch angle production (8 to 32 degrees).  If you end up getting more batted balls at the 32+ level at the expense of fewer batted balls in the 8-32 sweetspot, then guess what: you are going to be worse.

And so with shifting, there's going to be a sweetspot for how often to shift.  More is not always good.  More can actually be bad, once you are beyond the sweetspot.

Thursday, June 25, 2020

Could Dave Winfield have been a poor fielding outfielder?

A Bill James guest writer suggests that WAR must be broken, yada yada yada the same song and dance. The only evidence he offers is Gold Gloves. Here is my response.

Just as a for instance, in 1990, Dave Winfield is shown as -19 runs relative to the average RF, which is a terrible terrible number. Is it possible?

Well, Winfield had 1.70 putouts per 9 innings. The other Angels RF, Dante Bichette, had 2.22 po/9. The league average RF was 2.23. That’s our starting point, based on the facts. And the facts are that Winfield caught 0.5 fewer balls per 9 innings than his peers.

Winfield played for 920 innings, which is the equivalent of 102 9-inning games. And 102 games x 0.5 balls per game is 51 balls. That’s based on the facts. So far, all I’ve done is state facts.

Catching 51 fewer balls than your peers is a terrible terrible number. Very very terrible. How many runs should that be? Knowing nothing about anything, that should be about 40 runs. Total Zone at Baseball Reference suggests 19 runs.

How about for his career? Using facts only: 2.01 putouts per game in RF compared to the average of 2.15. Using facts, that 0.14 fewer putouts per game. And 15960 innings is 1773 games. Still only facts. And 1773 x .14 = almost 250 fewer outs. Those are the facts.

How many runs should that be? Knowing nothing about nothing, I’d say 200 runs.

Wednesday, June 24, 2020

Common baseline for Fielders

Roughly speaking, first basemen convert 75% of the plays they are responsible for into outs.

Roughly speaking, center fielders convert 75% of the plays they are responsible for into outs.

Does this mean the average 1B is equal to the average CF in converting plays into outs? No. Obviously we have a degree of difficulty. If this was Darin Erstad, it would be closer to 85% if he played 1B and 80% if he played CF. What we need is a common baseline. We are NOT talking about “what if Keith Hernandez played CF”. That’s not what we are talking about. We are taking one player, or a small group of players, taking those players, and moving them around the field. We are creating a common baseline. Let’s call this non-existant player Willie Kelly. Willie Kelly is not even an average fielder. He’s a below average fielder. He makes for a terrible shortstop, and acceptable fielder at 1B.

What we do is ask: how many plays would Willie Kelly make at each position.

• The average 1B makes 75% of the plays. Willie Kelly makes 70%
• The average 3B makes 70%, while Willie Kelly makes 60%
• The average 2B makes 65%, while Willie Kelly makes 55%
• The average SS makes 65%, while Willie Kelly makes 53%
• The average CF makes 75%, while Willie Kelly makes 65%
• The average RF makes 67%, while Willie Kelly makes 59%
• The average LF makes 65%, while Willie Kelly makes 59%

Now, don’t hold me to all those numbers. I rounded some here and there, as I’m just going to make a point. And the point is that each fielder has his own context, his own degree of difficulty. And you can’t just look at outs per play. You can’t look at the average for that position. You need a common baseline. You can make the argument that you want a fairly low common baseline, someone like Willie Kelly. Or maybe you want something a bit higher than that. Maybe a better baseline is William Kelliman. Maybe this is what we want:

• The average 1B makes 75% of the plays. William Kelliman makes 73%
• The average 3B makes 70%, while William Kelliman makes 65%
• The average 2B makes 65%, while William Kelliman makes 60%
• The average SS makes 65%, while William Kelliman makes 59%
• The average CF makes 75%, while William Kelliman makes 70%
• The average RF makes 67%, while William Kelliman makes 63%
• The average LF makes 65%, while William Kelliman makes 63%

Still, the point remains: common baseline. And I think this is what Bill James is after in his article. And if so, he’s right. If that’s not what he’s after, that’s fine, because the above is how I approach it. That’s how I evaluate fielding: against a common baseline.

What you CANNOT do is look at the BATTING production for each fielder and use that. Pete Palmer was wrong about very few things. This was one of them. But as Bill noted in his article:

When Pete Palmer first explained this idea to me, in a letter probably in 1976, I thought, “OK, well, that’s clever; we can use that until we figure out some way to determine the ACTUAL defensive value of a shortstop.” The problem is, we never did. As Sabermetrics grew, it just skipped over that problem. Pete had offered a way to work around the absence of knowledge, so people said, “OK, that’s good; let’s go with that.”

Bill is right. It was a useful stand-in, a placeholder until we can figure it out. And Bill actually had a better approach, one based on the Fielding Spectrum. And that is basically the approach I follow, somewhat roughing out those edges. And my approach is basically what the others have refined on their side for WAR. What Bill does is pretty close to what I do. What Fangraphs does is pretty close to what I do. And what Reference does is pretty close to what I do. We have a pretty close agreement. It just hasn’t been really laid down too strongly on paper, if only because there are still some rough edges, notably with catchers.

Anyway, that’s where we are.

UPDATE (for clarification):

We are leaving Keith Hernandez at 1B and comparing him to Willie Kelly.

We are leaving Ozzie Smith at SS and comparing him to Willie Kelly.

We are never, EVER comparing Ozzie and Keith both at SS or both at 1B.  That’s what we are NOT doing.

This is no different than “common opponents” comparison of two teams that never face each other.  That’s what we are doing here.

Sunday, May 24, 2020

Catcher WOWY

In 1979, in games started by Gary Carter, the Expos allowed 463 runs and made 3705 outs, for a runs per 27 outs of 3.37. That season, in games started by his backups, the Expos allowed 5.08 runs per 9 IP.  That difference is a whopping 1.71 runs per 9 IP, or 66% as much as his mates.

However, Carter had 136 starts compared to the 24 from his mates.  In terms of the WEIGHT of that 1.71 difference, we would use the harmonic mean, which is 41 games (or 1073 outs).

We can go through every season of his career and repeat this process.  And in his career, his weighted runs allowed is 86% of that of his mates (3.66 RA / 9IP with Carter starting compared to 4.28 when his mates start).  In other words, his team has allowed 0.62 fewer runs to score per 9 IP, when Gary Carter started the game behind the plate, compared to his mates that season.

Gary Carter started 1954 games (or if you use outs, the equivalent of 1964 9-inning games).  And 0.62 runs per game times 1964 games (unrounded) is 1204 fewer runs allowed.  That is the best figure in the last 100 years.

Using this method, here are the top 11:

• 1204 runs reduced: Gary Carter
• 1004: Mickey Cochrane
• 961: Tony Pena
• 871: Yadi Molina
• 807: Brad Ausmus
• 757: Andy Seminick (who??)
• 750: Rick Ferrell (who??)
• 701: Johnny Bench
• 682: Jason Varitek
• 652: Al López (who?? he did have MVP votes in 7 seasons)
• 647: Russell Martin

Fans of WOWY will recognize this as...well, WOWY.

The main problems, at least for THIS iteration, are as follows:

• Are the backups of Gary Carter disproportionately worse than the backups of Cochrane and Pena and so on?
• Was Gary Carter paired disproportionately with the best pitchers on his staff, compared to his mates?
• How much can Random Variation affect these results?

The Random Variation one is a big one.  In the Gary Carter starts, his teams allowed 7246 runs.  And since this is 1204 lower than his mates, his mates would come in at a pro-rated 8450 runs.  Just because we've OBSERVED 8450 (pro-rated) runs doesn't mean that's the true rate.  How much Random Variation is there in runs allowed?  I should figure it out at this point, but let's say it's one standard deviation is 3 runs per game.  With 1964 starts, you take the square root and multiply by 3 runs and that gives you 133 runs.  Since we have observations on both Carter and his mates, the Random Variation of the DIFFERENCE is 133 times root 2, or 188 runs.  So, based on that number 3 that I totally made up, we can reduce the 1204 by twice 188 runs due to Random Variation (for 2 standard deviations).  That still leaves us with a whopping 828 runs lowered.  So, whatever you can say RAndom Variation contributes to the noise in that 1204 runs, it won't be able to wipe away even half of it.  Most of it is real.

Anyway, that's all I've got for Iteration 1.  If an Aspiring Saberist wants to take it from here, go for it.

***

Note: reason I started this was because of Ryan Doumit, since he was getting hurt by the framing numbers.  Using this method, his teams allowed 188 more runs.  And if you go all the way to the bottom of his Fangraphs page:

And look right under the Defense column, all the way to the last line, you will see this number: -178 runs.  In other words, this WOWY method (188 runs) supports the evaluation of Doumit and his framing numbers (178 runs)!

***

Note 2: since someone will ask, Mike Piazza was better than his mates by 322 runs.  Make of it what you will.  I just know whatever number this method spit out, someone is going to complain.

Saturday, April 18, 2020

How do fielding systems work? (part 2)

If you haven’t read it, I recommend reading Part 1 first.

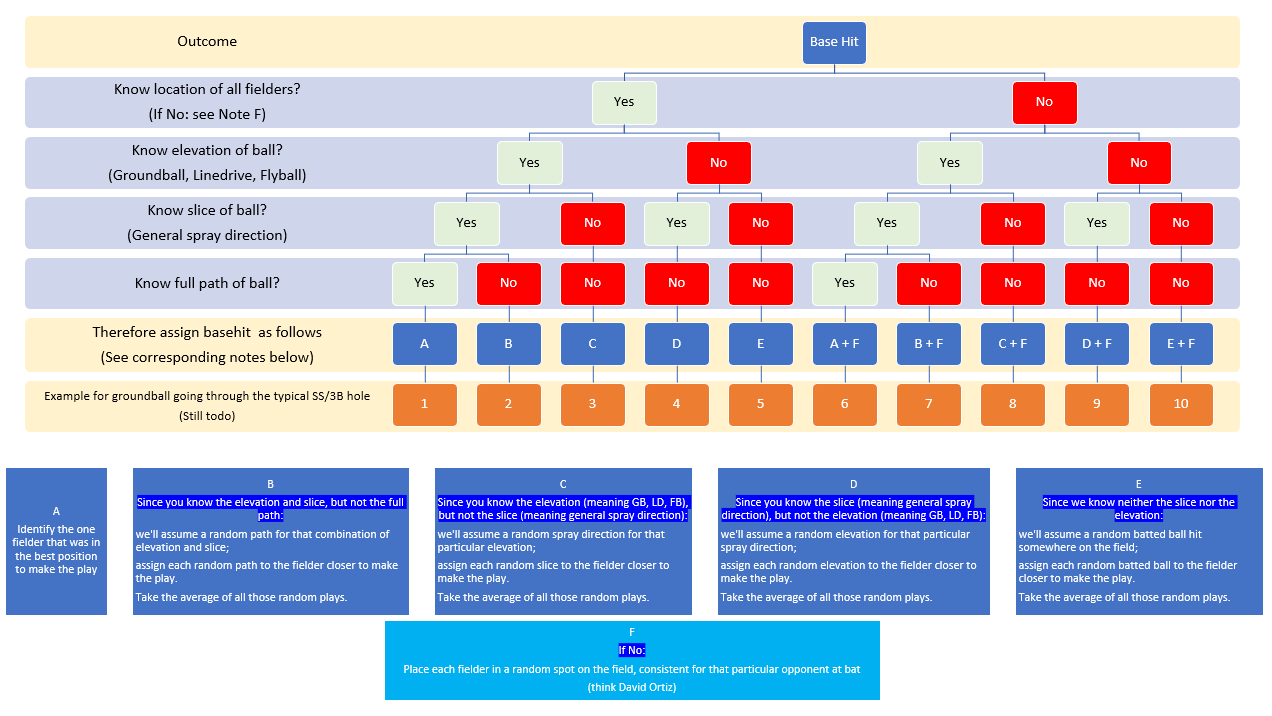
Let’s walk through this play (link on Savant, go watch that first please), and the ten paths we can follow in assigning ownership of this batted ball to the fielder.

First we’ll take the five paths: If you know the location of all the fielders.

A: We know everything about this batted ball, so this base hit belongs 100% to the 3B

B: We know it’s a groundball, and it was hit in the traditional-SS slice, so this base hit belongs 100% to the 3B

C: We know it’s a groundball, but we don’t know its slice. Therefore, we assign responsibility to the four infielders based on the bat-side of the batter. I won’t run the numbers, but for illustration purposes, it’ll be something like:

• 0.20 1B
• 0.40 2B
• 0.30 SS
• 0.10 3B

In other words, without knowing where the ball is hit, other than it’s a groundball, but we do know where the fielders are standing, we are taking an educated guess.

D: We know its slice is the SS/LF-gap, but we don’t know whether it’s hit on the ground or in the air. For illustration purposes, it’ll be something like:

• 0.35 LF
• 0.35 CF
• 0.30 3B

In other words, another educated guess as to the ownership of this basehit.

E: We know nothing about this batted ball, other than it’s a base hit. So, ownership will be something like:

• 0.10 1B
• 0.15 2B
• 0.15 SS
• 0.10 3B
• 0.10 LF
• 0.15 CF
• 0.25 RF

So, all that was knowing the location of the fielders, and knowing various degrees of information of the batted ball.

Now, let’s look at the next five paths based on not knowing where any of the fielders are.

And therefore, what we SHOULD do is take all known seven-fielder alignments (from the standard alignment that we all know to the overshift that has become prevalent, and everything in between), and run through our scenarios for all those hundreds of possible alignments. And then weight our results based on how frequent those alignments occur, for our given batter, park and game situation.

But for Blog Purposes Only, we’ll just choose ONE fielder alignment, the standard fielding alignment for LHH. And we do this especially because many fielding systems (implicitly) operate under this assumption.

A+F: We know everything about this batted ball, but we don’t know anything about the fielders. So, we assign ownership of this ball 100% to the SS. That’s right, the SS. That’s because that’s where the SS normally would be. Remember, we don’t know where the fielders are, so we have to place them somewhere.

B+F: We know it’s a groundball, and hit toward the SS slice: we assign ownership of this ball 100% to the SS. You are seeing the problem, right?

C+F: We know it’s a groundball, but that’s it. Since it’s a LHH, we’ll split along these lines:

• 0.25 1B
• 0.55 2B
• 0.15 SS
• 0.05 3B

D+F: We know its slice is the SS/LF-gap, but we don’t know whether it’s hit on the ground or in the air. For illustration purposes, it’ll be something like:

• 0.35 LF
• 0.35 CF
• 0.30 SS

In this case, the 3B goes away, and the SS takes his place.

E+F: We know nothing about the ball, or the fielders. Just that it’s a basehit. So, we split fairly evenly:

• 0.10 1B
• 0.15 2B
• 0.15 SS
• 0.10 3B
• 0.15 LF
• 0.20 CF
• 0.15 RF

***

So, what does all this mean? Well, it means that the less you know, the more you will shift ownership of the base hit from the 3B to one or more of the other fielders. And therefore, it automatically means that you are going to be wrong, to some degree or other.

How wrong? Well, when we know everything about everything on this play, it should be 100% ownership to the 3B. So as you go through the ten paths above, you can see how wrong you are, by seeing how much away from that 100% 3B you are.

For this particular play, it looks like this, in terms of ownership of the play going to the 3B:

• 100%: A
• 100%: B
• 30%: D
• 10%: C
• 10%: E
• 10%: E+F
• 5%: C+F
• 0%: A+F
• 0%: B+F
• 0%: D+F

So, the only time you are 100% right requires you to know the location of the fielders, and as much as the trajectory as you can.

And when you know nothing about the location of the fielders, the BEST you can hope is to be wrong 90% of the time, with a good chance of being wrong 100% of the time, ESPECIALLY if you know too much about that batted ball!

Tuesday, April 14, 2020

How do fielding systems work?

It starts with identifying for every batted ball the assignment of those plays based on whether they are outs, errors, or base hits.  

1. For outs, it is relatively straightforward: whoever is the first touch fielder is assigned the play.  It's not 100% true, but it's close to that. (An example of where it would not be is when a 1B pulls down an errant throw. So in those cases, we transfer ownership from first-touch to last-touch.)
2. For errors, it is relatively straightforward: whoever is awarded the error is assigned the play.
3. For hits, it's a bit more complicated. I started writing it out, but it started to become complicated.  So then I had the idea to do a flow chart.  Hopefully, the chart below makes it easy enough to follow, without it being overwhelming.

Next time, I'll come up with examples.  And then after that, show you how the expected out rates are established.

Click to embiggen

Sunday, April 05, 2020

Splitting responsibility between pitchers and fielders

Batters

From 2015-2019, the spread in BACON (batting average on contact) is one standard deviation of 40 points. This is for all batters with at least 100 balls hit into play (HIP). The average number of HIP was 294, and therefore we can establish that Random Variation would account for a spread of 28 points.

If we observe a 40 point spread, and we know that Random Variation accounts for a 28 point spread, then the remaining difference is 29 point spread. (That’s 29^2 = 40^2 - 28^2.) Of that 29 point spread, 13 points can be accounted for by the park. And therefore, the difference of a 29 point spread and a 13 point spread is a 26 point spread.

In other words, the TRUE TALENT spread in BACON for batters is one standard deviation = 0.026.

Thanks to a suggestion by Straight Arrow Reader GuyM, I repeated the above for xBACON. In other words, rather than taking the observed batting average on contact, I instead rely on the Statcast speed+angle quality of contact equivalency. The observed spread was much lower, at 31 points.

Random Variation accounts for 17 points.

A little sidenote. For binary results of BACON, one standard deviation for one batted ball is root of .343*(1-.343), whereby the .343 represents the average BACON. And so, one standard deviation is 0.47. However, for xBACON, it is not a binary outcome. Taking the standard deviation of every xBACON value, we get 0.29. (Which also happens to be the standard deviation of a uniform distribution.)

Park variation on xBACON accounts for 6 points.

So, with a quality of contact 31 point spread, a random 17 point spread, a park 6 point spread, that leaves us with a true 26 point spread. Which is the same number that we got from the outcome method.

Pitchers and Fielders

I repeated all this for pitchers, but this time I removed all HR. So rather than all contacted balls, it is only balls in the field of play (BIP). The true spread based on the observed outcome is 17 points, while the true spread based on the quality of contact is 13 points.

Now, why would these be so different, while the batter ones were identical? Fielders(*). While we accounted for the parks, we did not account for the fielders. And how can we account for the fielders? Well, the quality of contact establishes the spread for the pitchers. That’s 13 points. And therefore, the missing variable, what gets us from a spread of 13 points (using quality of contact) to a spread of 17 points (using observed outcomes) is the fielders. And since 11^2 = 17^2 - 13^2, then we can say that the spread in fielding is one standard deviation = 0.011.

(*) I may say Fielders here, but I actually mean Fielding.  That's because the way I handle Fielding, it's a combination of Fielder skill and Fielding Alignment (which I treat as a team influence).

In other words we have this:

• 36^2 (Observed Spread)
• = 29^2 (Spread from Random Variation, given 250 BIP)
• + 13^2 (Spread from Pitching)
• + 11^2 (Spread from Fielding)
• + 13^2 (Spread from Parks)

In other words, we can establish that each of the pitcher, fielding, and park are roughly similar in impact to the outcome of a ball in play. But more than all of them combined is good ole Random Variation.

And so, if you tried to partition responsibility based on a “left over” approach, whereby you account for two of Pitching, Fielding, Parks, and assign the remaining result, that last variable will absorb the entirety of the Random Variation. Which is almost certainly what you don’t want to do.

My preference is to just leave Random Variation unassigned. But if you must assign it to something, you may as well do it proportionally to the other three variables (Pitching, Fielding, Park).

Friday, April 03, 2020

Systematic bias in fielding metrics: when old school stats are actually more reliable

Thought exercise

Suppose you have 10 teams that ALWAYS shift their infielders. Not half the time like the Dodgers,who lead the league. I mean all the time. Against LHH, the 3B plays in short RF, and the SS plays on the right side of the bag. Against RHH, the 2B plays on the left side of the bag. I’ll call these teams The Shifters.

And suppose you have 20 teams that NEVER shift their infielders. Not 13% like the Cubs, lowest in the league. I mean NEVER. In other words, all the infielders are where tradition would dictate. I’ll call these teams The Traditionalists.

Now, since The Shifters and The Traditionalists are playing against the same teams, they all face a similar distribution of batted balls. Suppose that The Shifters are getting a few more outs out of their infielders against LHH, but they’ve overshifted and getting a few less outs against RHH. In other words, overall, there’s the same number of outs.

Let’s further suppose that the 3B on The Shifters are converting 3 outs per game, and the 3B on The Traditionalists are ALSO converting 3 outs per game. It’s just that the 3B on The Shifters, against a LHH, are getting them all from short RF, while against RHH they are all closer to the 3B line. The 3B outs against The Traditionalists are all where you’d expect them.

Enter The Zone

The way “zone” systems work is that they assign a “zone of responsibility”. They decide which zone each OFFICIAL POSITION is responsible for. The “official position” is technically the fielding position on the batting lineup. And they figure that out based on those zones that each position is converting plays into outs. Since the short RF position has plays being converted into outs not-often (only 10 of the 30 teams have their 3B there against LHH, and none against RHH), that zone does not belong to any infielder.

So, these zone systems have a numerator (outs) and denominator (plays) for all the zones where an OFFICIAL POSITION owns. What happens to outs made “out of zone”. In some systems, it gets added to the numerator only. In other systems, it gets added to both numerator and denominator. What happens to hits “out of zone” of the 3B? Well, those either go to the “in zone” of one of the infielders, or they just go away altogether. In other words, a basehit by a LHH to short RF against The Shifters that is not in-zone to the 2B is ALSO NOT in-zone to the 3B. This basehit disappears. The denominator for The Shifters just got lower.

For a zone-based system with a league of 10 The Shifters and 20 The Traditionalists, this is a systematic bias. And the more data you have, the worse it is. That’s because the more data you have, the less Random Variation there is, and the more the Systematic Bias will expose itself.

Exit The Zone

An old-school system doesn’t have this issue. That’s because EVERY batted ball is assigned to a fielder. All basehits are, effectively, shared among all seven fielders, regardless of where the fielders are, or the ball went. You may think this is a problem. And, in the short-run, it is. But given 5 or 10 or 15 years of data, that Random Variation will get reduced substantially. And so, if you have 3 outs per game being made by 3B among The Shifters and 3 outs per game by 3B among The Traditionalists, they will all look the same. That’s because the OFFICIAL POSITION is what is being held responsible not where they are standing. This makes no sense on a single play level. This is still a systematic bias. It’s just a different kind of systematic bias than a zone-system.

Where are we today?

Now, all of that is theoretical. The point of all that is to understand how things work. Where are we in 2019? I don’t know. That’s where The Aspiring Saberist comes into play. Hopefully, that’s one of you reading all this.

With regards to the way Statcast works: we remove positioning altogether. And so, the area of responsibility is where you are actually standing for that particular play. If a 3B is in short RF, he is not a 3B. He is “fielder in short RF”. We don’t care about his official fielding position on the batting lineup card. Just saying that should make it clear why we can’t use his official fielding position on the batting lineup card. That’s not how responsibility works. Where you stand IS what you are responsible for. So, whether your official fielding position on the batting lineup card is 2B, SS, or 3B, and you are standing in short RF, then we use that Fielder Role to establish responsibility. Your Role establishes your Responsibility.

Wednesday, March 25, 2020

Statcast Lab: Is there a different run value needed based on the infield slice?

One of the things that we’ve done in the long past is to give a different run value for 1B/3B, compared to 2B/SS. The idea was simple enough to understand: if a 2B or SS allowed a hit, it was likely a single. And if it was a 1B/3B, there’s a chance that it could be an extra base hit down the line.

Seems reasonable enough. So, what we ended up doing, in the long past, was to give .75 runs per play for 2B/SS and .80 runs for 1B/3B. Again, seems reasonable enough.

I looked at the Outs Above Average (for infielders only; I’ll do outfielders later today or tomorrow). And while the direction of that theory holds, the magnitude does not hold quite as much. For the 2B/SS roles, the impact of their play is -.005 runs, compared to the average infield play. While for the 1B/3B roles, the impact of their play is +.010 runs, compared to the average infield play. (The overall WEIGHTED average is 0, and you get there because there’s about 2X the plays at 2B/SS compared to 1B/3B).

So, the end result is that the gap in runs between the middle infielders and the corner infielders is about .015 runs, not the presumed long past value of .050 runs.

Why would that be? It’s probably easiest to say that 5% of the “assigned hits” are extrabase hits. But as we know, there’s alot more than just 5% hits that are extrabase hits, even if we limit it to the infield. For example, almost 10% of groundballs are extra base hits. So why the discrepancy? Well, half of those groundball extra base hits are “automatic hits”. In other words, they are hits not because the fielder wasn’t good enough to get there, but rather, his POSITIONING didn’t allow him for a chance to get there. And since Outs Above Average takes as an assumption of fact that the positioning of the player is not a skill of the player (easier to believe these days with shifting), then those auto-hits are not opportunities for the player. They end up being noise.

When we get to Layered Hit Probability (and by extension Layered wOBA), we will recover those “lost” hits, and be able to properly assign them to “team fielding alignment”. But, for the Outs Above Average metric, those aren’t in play (no pun intended).

Ok, so you may be thinking,we lost half, so maybe instead of the long past value of .050 runs, maybe it should be .025 runs? That is a good thought. Except, alot of those remaining extra base hits that are assigned to the fielder are “really difficult”. In other words, they remain in the pool for the player, but the hit probability is so low that they have limited damage to the fielder.

So, if you want a quick summary: the kind of hit that an infielder is responsible for is almost always a single. And because of that, when you look at outs saved, the translation to runs saved will be almost identical for middle infielders as for corner infielders.

Next time, I’ll compare IF to OF.

Tuesday, January 14, 2020

Statcast: Do fielders perform worse when they are in a Shift formation?

?The theory would be that by being out of position, a fielder will have less familiarity with a situation and so will perform worse than his "natural" location. If this is true, we should see it in Outs Above Average. I did something fairly simple: what is the OAA for a TEAM INFIELD if we have the shift on? And what is the OAA for a TEAM INFIELD if all the fielders are in their standard location?

Note: A shift is any formation where you have 3 or more infielders to one side of the bag.

So, there is an effect and in the direction you'd expect. But not the magnitude. When an infield is playing in its standard formation, they convert 0.0003 more outs per play. With about 2000 plays a season, that works out to 0.6 more outs per season. Hardly a number to worry over, even if you can make the case that it is "true" that they perform "worse".

HOWEVER. However, because shifts are disproportionately set with a LHH, we can break down the OAA of the team infield between LHH and RHH. And when we do that, well, things start to change. With a RHH, the infield does perform better in its standard formation, by a whopping 0.006 outs per play, which is 12 plays per season. Since a shift with RHH essentially means moving the second baseman from the right side to the left side, it is that positioning that we can narrow down as the culprit. This is also consistent with other research I've shown in the past where the performance of RHH on shifts is noticeably worse for the fielding team.

As for LHH, the OAA is slightly BETTER when the infield is in a shift formation, by 0.0026 outs per play, or 5 outs per season. At this point, the "familiarity" issue likely no longer applies, given that one-third of LHH plate appearances are being shifted. This may also explain why LHH on shifts is somewhat better for the fielding team: in addition to getting the fielders in a better spot, they perform slightly better when in those spots.

This is all preliminary, so it'll be interesting to break this down in the coming weeks and months.

Update: I should note that I did not control for the quality of fielders.  So, if a team that shifts more happens to do so with better fielders with LHH, then that would explain the results we see.  And if a team that shifts more happens to do so with WORSE fielders with RHH, that would ALSO explains the results we see.  As I said, this is the first step.

Thursday, January 09, 2020

Statcast Lab: How much do we want to adjust for the direction of a batted ball?

This is what has been perplexing me for months.  Is this a bias we want to remove, or retain?  That shows the OAA (Outs Above Average) for balls hit in the hole.  The black line is pretty sweet at 0.  But the bLue (for left, or 3B) is above average and the Red (for right or SS) is below average.  And this IS what we'd expect: for balls that both players can reach, the 3B will have a better shot at getting the runner than the SS, simply based on the running direction.  The 3B is closing the distance as he gets the ball, while the SS is enlarging it by the time he releases it.

Therefore, do we want to adjust this "bias"?  When Fred Lynn, LHH, faces a RHP, he has an advantage over Jim Rice, RHH.  But, we don't adjust that away, since being a LHH is part of Lynn.

We could make the argument that since the Rockies are positioning Story and Arenado, that Story has no choice.  So, we can't penalize him.  But, all fielders have some leeway, pitch to pitch to move around, as they respond to expected pitch types and locations and runner leads.

So, a ball may be hit halfway between Story and Arenado, but that's only AFTER Story and Arendo take their spot on the field.  Because of the nuanced nature of being able to move two or three steps in response to the pitch call and runner movement, what we'd actually want is the pre-nuanced, club-controlled spot for each fielder.  Which is unknown.

If we remove the bias altogether, and make SS and 3B equal on these plays, we are saying that SS and 3B are equal in getting to balls in the hole.  Which we can only say if we add the condition of "compared to other players at their locations, not to each other".

And that chart above is going to look kinda confusing if you see the black, red, and blue lines all sitting one right on top of the other.

What would YOU like to see?

When is a gimme not a gimme? Statcast Infield Defense style.

Tatis on similar plays: 111 plays made only 101 outs (91%) compared to an expected 107, or -6.

In the outfield, the vast majority of the OAA is based on 2+ star plays.

In the infield, HALF the value is on 90%+ plays.  This is because the chance of a misplay is so much greater on groundballs than airballs.

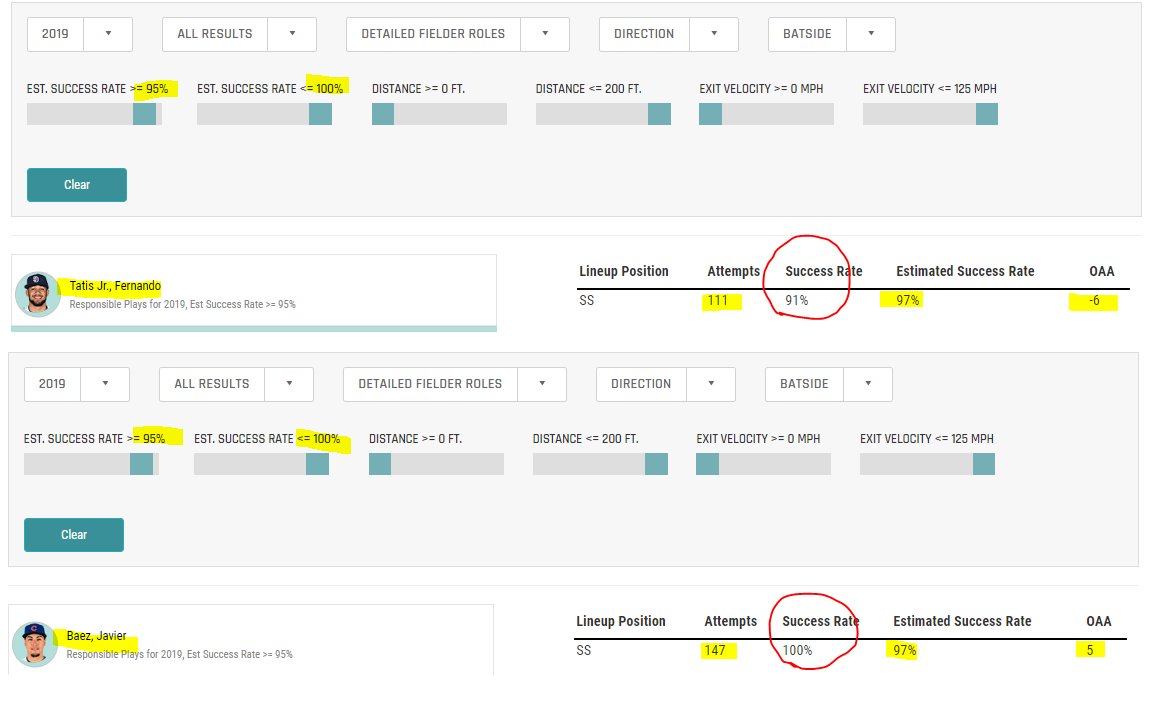
Making the routine play has tremendous value.

In case you missed it, you can slice/dice right here.

Statcast Infield Defense: Q&A

?Lots of excellent question everywhere on the newly released Infield Defense metric.  Twitter, Reddit, and at BTF among the places I've seen so far.

What I'll do is create a Q&A based on the questions or issues being raised.  I'll start with BTF, and go as far as I can before I go to bed, then pick it up in the morning.  I'll create one Q&A per comment.  So, check it out below in a few minutes.

Wednesday, January 08, 2020

Statcast Lab: History of the Fielding, now with Statcast Infield Defense

?Primer article by Mike on MLB.com

Savant main page by Daren, along with drill down and player pages, with Jason bringing the data together.

My tech blog post: a slimmed down web version, and the expanded downloadable PDF.

Sunday, November 24, 2019

Statcast: Catcher Framing and Called Strike Rate in The Shadow Zone

?In an excellent article on Catcher Framing, Mike created this image at the team level, which shows the percentage of called strikes in The Shadow Zone. 

He further pointed out:

The top team, Arizona, and the bottom team, Chicago, each had a nearly identical amount of takes in that area, 4,819 for the D-backs and 4,803 for the White Sox. Yet the D-backs, led by good framing from Carson Kelly and Alex Avila, had over 400 more called strikes there.

This puts the impact in stark terms.  Looking at the called strike rate in The Shadow Zone, one catching team can get 200 more strikes than the average team, while another catching team can get 200 fewer strikes.  How much value CAN a strike have?  I can tell you the answer is 0.125 runs per called strike, and so, we're talking about +/- 25 runs.

But, let's describe it in something a bit cruder, but with more relevance. If you think of 3 strikes being a strike out, and 9 strikes being an inning, then 200 called strikes would be about 22 perfect innings.  Each inning generates an average of 0.5 runs, and so, a clean inning saves you 0.5 runs.  If you have 22 of those, then you've saved 11 runs.  That's the crude way.  The better way is 0.125 runs per called strike.

As for simply relying on the called strike rate in The Shadow Zone, we can compare that to the runs saved on the strike calls per 100 pitches.  As you can see, an extremely strong relationship.  Indeed, an r of close to 0.95.  So, if you are having a tough time buying into Catcher Framing and runs and how all that is derived, you can take the first step and simply look at its most basic: percentage of pitches called strike in The Shadow Zone.  If you can do that, you'll be 90% of the way there.

?

(Click to embiggen)

Monday, October 21, 2019

Statcast Lab: Catcher Framing, WOWY at the Individual Game-Level

On Sept 15, 2008, at PNC Park, Dodgers catcher Russell Martin caught 19 called pitches in the inside part of the Shadow Zone. That would be zones 11 through 19, within the green dotted line.

While today, those are called strikes almost 80% of the time, it wasn't the case back in 2008. That could be any combination of the umpires improving over time and the tracking system improving over time. So, it would be more accurate to say that he caught those 19 pitches in the reported region noted above. Of those 19, 14 were called strikes.

In that same ballpark on that same day, his teammate A.J. Ellis was also catcher, as was opposing catcher Ryan Doumit. Those catchers caught 18 pitches in the same reported region, but got only 4 pitches called strikes (or 22.2%). Had Martin got the same calls, he would have gotten 19 x 22.2% = 4.2 strikes, instead of his actual 14. In other words, he got 9.8 more called strikes than the other catchers that day in that park.

On April 2nd against the Giants at Dodger Stadium, in the outside part of the Shadow Zone, with Bengie Molina as his opposing catcher, he got 3 strikes out of 20 pitches compared to Molina of 7 for 13. That made Martin MINUS 7.8 strikes that day.

And so we can go through every single game in the same way, and tally up the results. In the Heart of the Plate, he was +63 strikes (+35 at Dodger Stadium, +28 away). However, we would NOT expect any venue bias because of the way we are directly comparing Martin to the other catchers in the same venue on the same day.

• In the inside part of the Shadow Zone, he was +43 at home, +45 away, for a total of +88.
• In the outside part of the Shadow Zone: +29 home, +7 away.
• In the Chase Zone: +39 home, -6 away.
• In the Waste Area: +1 home, 0 away.

All tallied up: +147 home, +74 away, +221 total. Each strike is about 1/8th of a run, and so those +221 strikes translates to +28 runs.

In a more elaborate process that considers more variables and the zone in a more granular fashion, Fangraphs shows +30 runs.

When I repeat this for every year, Martin's career comes out to +171 runs. Fangraphs has a very similar +166 runs.

As much as it strains the credulity to think that Martin's framing could have led to +28 runs, I also can't reject that conclusion. I can reduce that number somewhat for the uncertainty level of the measurement. But given the way I controlled for the metric, by directly comparing Martin to the other catchers in the same park on the same day, that's a tough call as well.

I could repeat the above by focusing on each individual bin and controlling for the pitcher, and potentially the batter. But that basically will put me on a path to replicate Fangraphs. And given that without doing any of that I ALREADY match Fangraphs, all I'd be doing is further matching Fangraphs.

So, I don't want to agree with the numbers, but I am forced to.

I should note that we don't see these wide numbers in the past few years. That could be any combination of the umpires improving and the tracking system improving.  It could also be that teams are now very aware not to have a Ryan Doumit behind the plate, so it could be improvement in catcher selection and coaching of catchers.  In other words, whatever inefficiencies exist, it's being slowly closed on all sides.

Wednesday, October 02, 2019

Statcast Lab: Cain v Taylor

This is the point at which Cain got the ball.

  ?

Runner is about 75 feet from 3B. Taylor Sprint Speed is 29 ft/s, meaning he needs 75/29 = 2.6 seconds

Cain will have to make an almost 200 foot throw. He has a somewhat below average arm at 85 mph. Here's where we need to leave the world of mph and enter the world of feet / sec. 85mph is 125 ft/s. That's at release. The ball will slow down in flight. Roughly speaking, it'll lose 10% every 60 feet. 

In this case, we'd do 200/60 = 3.33, and 0.9^3.33 = 70%. So at arrival, the speed of the ball is 70% of 125 ft/s or 88 ft/s. So the average speed of the ball in flight is about 106 ft/s. And so, a 200 foot throw will get there in about 200/106 = 1.9 seconds. (It's not this straightforward, but it's close enough.)

The exchange time (pickup to release) for a throw is about 0.5 to 0.75 seconds, which means that the ball would have reached the VICINITY of 3B in 2.4 to 2.65 seconds. It would have been close if the throw was on target. Which of course, it might not be.

How successful would Cain have been? Probably 60% if the throw is on target. And maybe it's on target 70% of the time? So, about 40% of the time he gets the runner maybe?

In the meantime, it would allow the batter to reach second base as the tying run. But, there were two outs! Making the third out at thirdbase is a cardinal sin for baserunners. Which makes it very appealing for the defense.

Let's work some MORE numbers.

http://tangotiger.net/we.html

Bottom of the 8th, 2 outs, down by 2 runs. Our choices are:

• runners on 1B and 3B (our baseline)

or

• runner on 2B and 3B
• end of inning

So, our baseline is a win expectancy for the Nationals of 15.8%.

• If Cain went for it and missed, then the win expectancy is 19.2%.
• If Cain got the out, then the win expectancy for the Nats is 7.1%.

In other words, the tradeoff is that the Nats gets +3.4% if Cain doesn't hit the target in time, or the Nats are -8.7% if Cain gets Taylor to end the inning.

All Cain has to do is make the play 28% of the time. That is:

• 28% of the time, the Nats lose 8.7% 
• 72% of the time, the Nats gain 3.4%

And that's breakeven.

Remember, we guessed that Cain would have gotten Taylor about 40% of the time, and he only needed to get him 30% of the time.

Cain should have gone to third.