人工知能フレームワーク入門(第2回):TensorFlowの基本的な使い方

人工知能関連のソフトウェアを実装するに当たって広く使われているのがGoogleが提供するオープンソースの数値演算・人工知能関連ライブラリである「TensorFlow」だ。今回はこのTensorFlowのアーキテクチャや、基本的な行列演算、CSVファイルからのデータ読み込み、機械学習プログラムの実装を行う流れを紹介する。
TensorFlowのアーキテクチャ
前回記事で紹介したとおり、TensorFlowは人工知能や強化学習を利用するシステムで使われるさまざまな部品を提供するライブラリだ。提供される機能としてはさまざまな行列・ベクトル演算、非線形演算関数、データファイルの読み書き、最適化問題を解くためのソルバー、ニューラルネットワークで使われる各種演算処理など多岐にわたる。
TensorFlowが一般的な数値演算ライブラリと異なるのは、計算グラフ(Computation Graph)というものを用いて処理を実行する点だ。計算グラフは有向グラフによって演算処理を表現したもので、グラフの頂点(ノード、node)が実行する演算内容、辺が各ノードの入出力を表す。
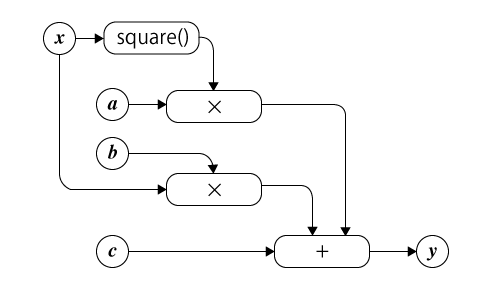
たとえばy = ax2 + bx + cという二次関数は、計算グラフでは図1のように表現される。

ここで、「square()」は入力された値の二乗(平方)を出力する操作、「×」は入力された値の積を出力する操作、「+」は入力された値の和を出力する操作を示しており、xの2乗とaの積、xとbの積、cを足し合わせたものがyになる、という関係性が定義されている。
ちなみに、TensorFlowでは「Tensor(テンソル)」という形式で数値を扱うようになっている。テンソルは行列やベクトル、スカラーといったデータを一元的に扱うための概念だが、とりあえず多次元配列として表現できるものすべてを扱えるものがテンソルであると認識しておけば良いだろう。
TensorFlowでは演算処理を行うためにまずテンソルを使った計算グラフを定義し、続いてその計算グラフに値を入れて計算処理を実行する、という流れで処理を記述する。TensorFlowという名前は、このようにテンソルを計算グラフでフロー処理する、ということから命名されている。
以下ではこういったTensorFlowのアーキテクチャを理解するための例として、シンプルな最適化問題を実装したプログラムを紹介しよう。
TensorFlowで線形回帰分析を行う
前述のとおり、TensorFlowは強化学習だけでなく、さまざまな数値演算や最適化問題を解くためにも利用できる。ここでは、TensorFlowを使って線形回帰分析を行う例を紹介する。
与えられたデータの組からその関連性を示す式を推測することを回帰分析と呼ぶ。これは、具体的にはn個のデータの組(x1, y_1)、(x2, y_2)、……、(xn, y_n)が与えられた際に、以下の関係性を満たす関数fを推測という問題となる。
yn = f(xn) + en
ここでenは誤差項と呼ばれるもので、(e1, e_2, ... e_n)は互いに独立で分散は一定、期待値は0という前提条件がある。
特に関数fが一次関数の場合は線形回帰分析と呼ばれ、さまざまな分野で用いられている。線形回帰では、xnおよびynがそれぞれスカラーの場合、関数fは次のように表現できる。
yn = f(xn) = axn + b
ここでaおよびbは係数(パラメータ)であり、線形回帰分析はこのaおよびbの値を推定するという問題となる。そのためにもっとも一般的な手法が、最小二乗法と呼ばれるものだ。
最小二乗法は、enの2乗和を最小にするaおよびbを推定結果とするというものだ。ここで、enは次のように表記できる。
en = yn - f(xn) = yn - axn - b
これを踏まえると、これは以下のRSSを最小化するという問題に帰結できる(図2)。

TensorFlowのインポートと計算グラフの定義
それでは、上記の最小化問題を解くためのPythonプログラムを作成していこう。今回作成したプログラムの全文はOSDNの「TensorFlowサンプルコード」リポジトリで公開しているので、適宜参照してほしい。
まず、TensorFlowを利用するにはtensorflowモジュールをインポートする必要がある。このとき、「import tensorflow as tf」のようにして、tensorflowモジュールを「tf」という名称で参照できるようにするのが慣例だ。
#!/usr/bin/env python # -*- coding: utf-8 -*- import tensorflow as tf
続いて、計算グラフの定義を行っていく。まず、計算に使用する変数とプレースホルダを定義する。TensorFlowにおいては、計算グラフを処理している最中に変更できる/変更される値を変数と呼び、tf.get_variable()メソッドなどで定義できる。
今回の例ではaおよびbが変数となるので、次のようにこれら変数を定義する。
# 変数とプレースホルダの定義
a = tf.get_variable("a", shape=[1], dtype=tf.float32)
b = tf.get_variable("b", shape=[1], dtype=tf.float32)
get_variable()メソッドは複数の引数を取り、第一引数には変数名を指定する。ここで指定する変数名はメソッドの戻り値を格納する変数と必ずしも一致しなくともよいが、混乱を避けるため同じものを使用すると良いだろう。
また、shape引数はテンソルの形状(要素数)を指定するものだ。TensorFlowではすべての変数がテンソルとして扱われる。TensorFlowにおいてはテンソルの実体は1つ以上の次元を持つ配列であり、その形状は次のような配列で表現される。
[<1つめの次元の要素数>, <2つめの次元の要素数>, ... <3つめの次元の要素数>]
このルールに則ると、n要素のベクトルの形状は次のような表記となる。
[n]
また、m×n行列の形状は次のように表記できる。
[m, n]
今回、変数aはスカラーであり、これは要素数が1のベクトルに相当する。そのため、shape引数には「[1]」を指定する。
dtype引数にはデータの型(データタイプ)を指定する。指定できるデータタイプはtf.DTypeで定義されているので詳しくはそちらを参照してほしいが、今回は32ビット単精度浮動小数点である「tf.float32」を指定している。
次に、「プレースホルダ」を定義する。プレースホルダは、システムに入力されたデータを代入するための特殊な変数だ。今回の問題ではx、yがこれに相当する。プレースホルダはtf.placeholder()メソッドなどで定義できる。
x = tf.placeholder(name="x", dtype=tf.float32) y = tf.placeholder(name="y", dtype=tf.float32)
tf.placeholder()メソッドも形状を指定するshape引数や名前を指定するname引数を指定できるが、これらは省略可能だ。shape引数を省略すると、データの代入時に自動的に形状が決定されるようになる。
変数を定義したら、続いてこれらを使って計算グラフを構築する。計算グラフの構築は「+」や「-」、「*」などの演算子や、TensorFlowが提供する数値演算関数を使って変数の関係性を記述することで行える。たとえば誤差(y - a*x - b)の2乗和は、tf.square()メソッドを使用して記述できる。
square_error = tf.square(y - a*x - b)
なお、この文は「square_error変数に(y - a*x - b)の2乗を行った結果を代入する」という操作のように見えるが、実際にはこの文の評価時点では計算は実行されず、「square_error変数の値は(y - a*x - b)の2乗となる」という関係性を定義するだけである点には注意したい。実際の計算は、後述するセッションの実行時に行われる。
さて、今回の最適化問題では前述の通り誤差の2乗和に注目し、それを最小化するaおよびbを求めるという問題となる。それには、xおよびyのn個の組(x1, y_1), (x_2, y_2), ... (x_n, y_n)を与えてそれぞれの誤差の2乗を求め、それを足し合わせて誤差の2乗和を求めるという操作が必要となる。残差の2乗和(residual sum of squares、RSS)は、引数で与えられたテンソルの各要素の和を求める操作(reduce操作)を行うtf.reduce_sum()メソッドを使って次のように定義できる。
rss = tf.reduce_sum(square_error)
このようなシンプルな記述だけで残差の2乗和を計算できる理由だが、まず計算グラフの実行時に、変数xおよびyにxおよびyの組(x1, y_1)、(x2, y_2)、……、(xn, y_n)を次のように代入することを考えよう(図3)。

なお、TensorFlowにおいて、ベクトルは1次元(1行n列)のテンソルとして扱われる。そのため、ここではこのように転置形式での表現としている。
さて、aおよびbは一次元・要素数1のテンソル(スカラー)であるため、この場合「y - a*x - b」は次のようなテンソルとなる(図4)。

tf.square()メソッドは引数で与えたテンソルの各要素の二乗を要素として持つテンソルを返すメソッドで、tf.square(y - a*x - b)は次のようなテンソルを返すことになる(図5)。

前述のとおりtf.reduce_sum()メソッドは引数として与えたテンソルの各要素の和を求めるメソッドであるため、最終的にこれで残差の2乗和を得ることができる。
最適化アルゴリズムの準備
今回の目的は、RSSを最小とするaおよびbを求めるというものだった。そのためにはいくつかのアルゴリズムがあるが、ここでは最急降下法という手法を利用する。最急降下法とは、指定された関数の最小値をその関数の微分を使って求めるアルゴリズムだ。TensorFlowでは「tf.train」というモジュールでさまざまな最適化アルゴリズムが提供されており、最急降下法もこのモジュール経由で利用できる。
TensorFlowで最適化アルゴリズムを利用するには、そのアルゴリズムに対応したクラスのインスタンスを作成する必要がある。最急降下法では、「tf.train.GradientDescentOptimizer」というクラスがこれに該当する。tf.train.GradientDescentOptimizerクラスのイニシャライザは引数として学習率(解を探索する反復処理の際に、1反復あたりどの程度値を変更するかを指定するパラメータ)を与える必要があるので、適当な値を与えてインスタンスを生成する。学習率が大きいほど少ない反復数で解が求められるが、大きすぎると発散して適切な解が求まらない可能性があるので注意したい。
このクラスにはminimize()メソッドが定義されており、最小化したいパラメータを引数として指定してこのメソッドを実行することで最小化を行う計算グラフが構築される。解の探索は、この戻り値を後述するセッションで実行することで行える。
optimizer = tf.train.GradientDescentOptimizer(1.0e-5) minimize = optimizer.minimize(rss)
データセットの読み込み
今回のような最適化問題や学習問題では、問題を解くために既知のデータセットが必要となる。TensorFlowではさまざまな形式のデータを読み込むための仕組みが用意されているが、今回は簡単に用意できるCSV(Comma Separated Values)形式のデータを使用する。CSV形式はその名の通りカンマと改行でデータを区切る形式で、1行が1つのエントリとなる。
今回は以下のようなコードを用意して実験に使用するCSV形式のデータセットを生成した。このプログラムは引数として生成するデータ数を取り、その結果を標準出力に出力する。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import sys
import random
# 出力結果を一定にするため、常に同じ乱数の種を指定する
RANDOM_SEED = 314
random.seed(RANDOM_SEED)
# パラメータを指定する
a = 10
b = -4
X_RANGE = (-10, 10)
ERROR_RANGE = (-20, 20)
# 引数の数をチェックし、引数がなかったら終了する
if len(sys.argv) < 2:
sys.stderr.write("{} <number of output>\n".format(sys.argv[0]))
sys.exit(-1)
# 引数で指定された数だけループを回す
for n in range(0, int(sys.argv[1])):
# x, y, eを計算して出力する
x = random.random() * (X_RANGE[1] - X_RANGE[0]) + X_RANGE[0]
y = a * x + b
e = random.random() * (ERROR_RANGE[1] - ERROR_RANGE[0]) + ERROR_RANGE[0]
print("{},{}".format(x, y+e))
このプログラムを実行すると、次のようにxとyの組が出力される。
$ python generate_data.py 10 -6.07137449737,-80.2551145383 -9.94722476148,-98.3468044864 -5.31536766867,-68.8456912003 0.935515446704,3.34732255339 2.67689997374,9.93584617098 -7.84367057476,-92.6878007753 -9.440201529,-108.882840126 -4.90147291839,-64.6489382967 -3.01925520288,-21.5067231304 0.33737940858,2.03882556259
今回は100個のデータを生成し、これを「dataset.csv」というファイルに出力した。
$ python generate_data.py 100 > dataset.csv
ちなみにこのデータをプロットしてみると図6のようになる。ここで横軸がxの値、縦軸が各xに対応するyの値だ。

さて、CSVデータなどのテキストデータをTensorFlowで読み込むには、tf.train.string_input_producerとtf.TextLineReaderを利用する。これらを利用したファイル入力も、TensorFlow上では計算グラフを利用する。
まず、ファイルからテキスト形式で1行ずつデータを読み込むためのtf.TextLineReaderクラスのインスタンスを作成する。
reader = tf.TextLineReader()
次に、tf.train.string_input_producer()に引数として読み込みたいファイルのファイル名を格納した配列(ここでは「["dataset.csv"]」)を与える。このメソッドは指定したファイルからデータを読み出すためのキューを戻り値として返す。
file_queue = tf.train.string_input_producer(["dataset.csv"])
このキューをtf.TextLineReaderクラスのread()メソッドに引数として与えると、戻り値として読み込んだデータが渡される。
key, value = reader.read(file_queue)
ここで、keyには何行目のデータかという情報が、valueには実際に読み込んだデータが格納される。読み込んだCSV型式データは、tf.decode_csv()メソッドを使ってデコードできる。
col1, col2 = tf.decode_csv(value, [[], []])
ここで、第2引数(record_defaults引数)には読み出すデータのデフォルト値を指定する。デフォルト値を設定しない場合は、このように空の配列を指定する必要がある。
以上でCSVファイルから1行ずつデータを読み出すことができるのだが、今回の計算グラフでは前述のとおりプレースホルダ変数xおよびyに複数の値をまとめて格納する必要がある。そのため、tf.train.batch()という、指定した数のデータを取得し、それをまとめたテンソルを出力するメソッドを使用する。今回の例では次のようにして100個のデータを取得し、それをdata_xおよびdata_yというテンソルに格納している。
data_x, data_y = tf.train.batch([col1, col2], 100)
ここで第一引数では入力とするテンソル、第2引数では取得するデータ数を指定している。これで、data_xおよびdata_yにxとそれに対応するyの値の組が格納される。
ちなみにこの操作を計算グラフで表したものが次の図7だ。string_input_producerで読み込んだデータが、reader.read()、decode_csv()、batch()の順に処理されるという流れが分かる。

セッションの開始
TensorFlowでは、定義した計算グラフにデータを投入して実行することをセッションと呼び、セッションの開始や終了などはセッションを管理するためのクラスであるtf.Session経由で実行する仕組みとなっている。計算グラフに関する処理を開始するには、まずこのtf.Sessionクラスのインスタンスを作成する必要がある。
sess = tf.Session()
tf.Sessionクラスには引数で指定した処理を実行するrun()メソッドが用意されている。このメソッドの第1引数に実行したい処理や計算グラフを、第2引数に計算グラフへ入力する値を指定することで、その処理が開始される。また、引数にテンソルを指定した場合は計算グラフに基づいてそのテンソルの値が計算される。どちらの場合も、その結果がメソッドの戻り値として返される。
さて、実際の計算を行う前に、いくつかの前処理が必要となる。まず必要なのが変数の初期化だ。これは、次のようにtf.global_variables_initializerを実行すれば良い。
sess.run(tf.global_variables_initializer())
「global_variables」(グローバル変数)と名前が付いていることから推測できるとおり、TensorFlowでは独自の変数スコープを持っており、グローバル変数以外にもローカル変数(local_variable)やモデル変数(model_variables)などがある。
次に必要な前処理は、スレッドを管理するためのコーディネータ(coordinator)の準備だ。TensorFlowではtf.train.Coordinatorクラスがこの処理を担っている。
coord = tf.train.Coordinator()
セッションとコーディネータを用意したら、ファイル読み出しで使用するキューを開始するtf.train.start_queue_runners()メソッドを実行する。これによってファイルからデータを読み出せるようになる。
threads = tf.train.start_queue_runners(sess=sess, coord=coord)
以上の前処理が完了すると、ファイルの読み出しや定義した計算グラフの実行が可能となる。
続いて、計算グラフにデータを投入して計算処理を実行していこう。まず、ファイルからのデータ読み出しを行う。
dataset_x, dataset_y = sess.run([data_x, data_y])
計算グラフ上、data_xおよびdata_yはファイルからの入力を格納する変数として定義されているので、これによってファイルの読み出しが行われ、その結果がdataset_xおよびdataset_y変数に格納される。
また、aおよびbの初期値も設定しておく。変数に値を設定するには複数の方法があるが、ここではload()メソッドを使用した。ここではともに初期値を0.0としている。
a.load([0.0], sess) b.load([0.0], sess)
続いて、ループを回して解の探索処理を実行する。
# 初期状態のRSSを取得
result = sess.run(rss, {x: dataset_x, y: dataset_y})
print("RSS:", result)
# ループ開始
for i in range(10000):
for j in range(1000):
sess.run(minimize, {x: dataset_x, y: dataset_y})
# RSSを取得し、以前のものと比べて小さくなっていなかったら終了
result_after = sess.run(rss, {x: dataset_x, y: dataset_y})
print("RSS:", result_after)
if (result_after >= result):
break
result = result_after
print("done.")
ここでは、まず最初に初期状態でのRSSの値を取得して表示したのち、1000回の探索処理を実行する。続いてその前に取得しておいたRSSの値と探索処理実行後のRSSの値を比較し、RSSの値が収束するまでこの処理を繰り返している。なお、ここでは値が収束せず発散した場合に備えて、ループは最大1万回繰り返したら終了するよう設定している。
処理が完了したら、キューで使用されているスレッドに対し終了リクエストを送信するtf.train.Coordinatorクラスのrequest_stop()メソッドを実行し、続いてjoin()メソッドを実行してスレッドが終了するまで待機する。
# スレッドの終了待機 coord.request_stop() coord.join(threads)
最後に、推定結果などを出力する。今回は比較のため、データセット生成の際に使用したaおよびbの値を使って計算したRSSも出力するようにしている。ここでは変数に指定した値を代入するload()メソッドを使用している。
# 結果の出力
print("results: [a, b] =", sess.run([a, b]))
print("RSS is", sess.run(rss, {x: dataset_x, y: dataset_y}))
# データセット生成に使用したa、bの値を使用した場合のRSSを計算する
a.load([10.0], sess)
b.load([-4.0], sess)
print("true [a, b] is", sess.run([a, b]))
さて、このコードを実際に実行した結果は以下のようになった。
$ python liner_regression.py 2017-12-18 19:06:21.374642: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX RSS: 386664.0 RSS: 12661.7 RSS: 12597.6 RSS: 12596.2 RSS: 12596.2 RSS: 12596.2 RSS: 12596.2 done. results: [a, b] = [array([ 10.20032501], dtype=float32), array([-6.00651455], dtype=float32)] RSS is 12596.2 true [a, b] is [array([ 10.], dtype=float32), array([-4.], dtype=float32)] true RSS is 13227.2
テストデータ生成に使用したaおよびbの値は10および-4だが、推定結果は10.20033264および-6.00628662となっている。特にbについてはややズレた値となっているが、RSSの値についてはテストデータ生成に使用したa、bの値で計算した場合は13227.2だったのに対し、推定されたa、bの値で計算した場合は12596.2となっているため、最適化問題としてはこのa、bの値は適切と考えられる。
3層のニューラルネットワークを使った学習
さて、ここまでで説明したサンプルコードは強化学習とは関係のない、単なる最適化問題だった。続いては、3層のニューラルネットワークを使った分類システムをTensorFlowで実装してみよう。
今回の問題は、図8のような3×5ドットで表現される数字を学習させて認識できるようにするというものだ。ここで、各ドットは0か1の2つの状態を持つこととする。

ニューラルネットワークモデルの設計
前述のとおり、ニューラルネットは入力層と中間層、出力層から構成される。ニューラルネットをモデルとして使用するには、まず入力層に何をどのように入力するか、そして出力層は何をどのように出力するかを決める必要がある。
まず入力層だが、今回は3×5ドット(合計15ドット)のそれぞれの値をそのまま入力にすることとする。つまり入力層は15のノードから構成されることになる(図9)。

次に出力層だが、今回の問題では入力された数字が0~9のどれかを推定するという問題であるため、各数字に対する推定された確度を出力として取ることにする(図10)。この場合、確度が最も高い数字が最終的に推定された数字となる。

中間層については、今回は1層なのでそのノード数のみを設定すれば良い。今回は第1層と同じ15ノードに設定した。これらをまとめると、今回使用するニューラルネットの構成は図11のようになる。

テストデータの作成
学習に使用するテストデータは、次のようなプログラムで作成した(コード全文)。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# 10要素を持つ配列を作る
DATA = [0] * 10
DATA[0] = [1, 1, 1,
1, 0, 1,
1, 0, 1,
1, 0, 1,
1, 1, 1]
:
:
DATA[9] = [1, 1, 1,
1, 0, 1,
1, 1, 1,
0, 0, 1,
1, 1, 1]
for i in range(0, 10):
s = ",".join([str(x) for x in DATA[i]])
print("{},{}".format(i, s))
出力するデータはプログラム内にハードコードされており、それをCSV形式で標準出力に出力するだけのプログラムとなっている。出力されるデータは次のようになる。
0,1,1,1,1,0,1,1,0,1,1,0,1,1,1,1 1,0,1,0,0,1,0,0,1,0,0,1,0,0,1,0 2,1,1,1,0,0,1,1,1,1,1,0,0,1,1,1 3,1,1,1,0,0,1,1,1,1,0,0,1,1,1,1 4,1,0,1,1,0,1,1,1,1,0,0,1,0,0,1 5,1,1,1,1,0,0,1,1,1,0,0,1,1,1,1 6,1,1,1,1,0,0,1,1,1,1,0,1,1,1,1 7,1,1,1,0,0,1,0,0,1,0,0,1,0,0,1 8,1,1,1,1,0,1,1,1,1,1,0,1,1,1,1 9,1,1,1,1,0,1,1,1,1,0,0,1,1,1,1
ここでは各行の第1カラムが表現する数字、第2カラム以降がその3×5ドットでの表現となっている。今回はこのデータを「digits_data.csv」として保存した。
また、同様に検証用のデータを出力するコードも用意した(コード全文)。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# 10要素を持つ配列を作る
DATA = [0] * 10
DATA[0] = [0, 1, 0,
1, 0, 1,
1, 0, 1,
1, 0, 1,
0, 1, 0]
:
:
DATA[9] = [0, 1, 1,
1, 0, 1,
0, 1, 1,
0, 0, 1,
1, 1, 0]
for i in range(0, 10):
s = ",".join([str(x) for x in DATA[i]])
print("{},{}".format(i, s))
こちらでは、学習用のデータを微妙に変形させたものを出力するようになっている(図12)。

このデータを出力したものは次のようになる。こちらは「test_data.csv」として保存した。
0,0,1,0,1,0,1,1,0,1,1,0,1,0,1,0 1,1,0,0,1,0,0,1,0,0,1,0,0,1,0,0 2,1,1,0,0,0,1,0,0,1,0,1,0,1,1,1 3,1,1,0,0,0,1,0,1,0,0,0,1,1,1,0 4,0,1,1,1,0,1,1,1,1,0,0,1,0,0,1 5,1,1,1,1,0,0,1,1,0,0,0,1,1,1,0 6,0,1,1,1,0,0,1,1,0,1,0,1,1,1,1 7,1,1,1,1,0,1,0,0,1,0,1,0,1,0,0 8,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0 9,0,1,1,1,0,1,0,1,1,0,0,1,1,1,0
TensorFlowでのモデルの記述
それでは、この分類問題を解くコードをTensorFlowを使って記述してみよう(コード全文)。
まずはtensorflowモジュールの読み込みと、いくつかの前処理を行う。今回は入力層のサイズ(INPUT_SIZE)や第2層のサイズ(W1_SIZE)、出力層のサイズ(OUTPUT_SIZE)を変数として定義しておいてあとで変更できるようにした。また、tf.set_random_seed()メソッドで乱数の種を指定し、乱数を使った処理で毎回同じ結果が得られるようにしておく。
#!/usr/bin/env python # -*- coding: utf-8 -*- import tensorflow as tf INPUT_SIZE = 15 W1_SIZE = 15 OUTPUT_SIZE = 10 tf.set_random_seed(1234)
続いて、モデルを計算グラフとして実装する。まず、使用するプレースホルダx1およびyを定義する。x1は入力されたデータを格納するものであり、ニューラルネットワークの第1層に相当する。yは学習時に使用する正答データを格納するものだ。
x1 = tf.placeholder(dtype=tf.float32) y = tf.placeholder(dtype=tf.float32)
続いて、入力層と中間層(第2層)の関係を記述する。前回説明したとおり、入力層xと中間層x2には次の関係がある。
xn+1 = f ( Wn xn + bn )
今回、活性化関数(f()には汎用的な活性化関数として使われるシグモイド関数を使用する。シグモイド関数はTensorFlow内ではtf.sigmoidとして提供されている。これをTensorFlowで記述すると、次のようになる。
W1 = tf.get_variable("W1",
shape=[INPUT_SIZE, W1_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.05))
b1 = tf.get_variable("b1",
shape=[W1_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.05))
x2 = tf.sigmoid(tf.matmul(x1, W1) + b1)
ここでは、get_variableのinitializer引数としてtf.random_normal_initializerを指定することで、それぞれの変数の各要素をランダムな値に初期化するよう設定している。
また、前述のとおりTensorFlowでは1次元のテンソル(ベクトル)は1行n列の行列として扱われるため、「W1×x1」ではなく「x1×W1」という操作になる点に注意したい(TensorFlow上でのW1、x1は数式上のW1、x1を転置したものとなり、(W × x)T = xT × WTという関係があるため)。
続いて中間層と出力層の関係を記述する。出力層では、活性化関数にソフトマックス関数を使用する。ソフトマックス関数は分類問題でよく使われる活性化関数で、確率の形で出力を行えるのが特徴だ。TensorFlowではtf.nn.softmaxとして提供されている。
W2 = tf.get_variable("W2",
shape=[W1_SIZE, OUTPUT_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.05))
b2 = tf.get_variable("b2",
shape=[OUTPUT_SIZE],
dtype=tf.float32,
initializer=tf.random_normal_initializer(stddev=0.05))
x3 = tf.nn.softmax(tf.matmul(x2, W2) + b2)
以上でニューラルネットワークモデルの記述は完了だ。
続いて学習に使用する「コスト関数」を定義する。コスト関数は入力に対する出力と期待される出力がどれほど違うかを評価する関数で、この値が小さいほど正解に近い値が出力されていることになる。
今回はコスト関数として交差エントロピー(cross entropy)を使用する。こちらも分類問題でよく使われるコスト関数で、出力層の活性化関数にソフトマックス関数を利用する場合、その交差エントロピーは次の式で定義できる(図13)。

これは、TensorFlowでは次のように記述できる。前述のとおりyは正答データ、x3は出力層の出力だ。
cross_entropy = -tf.reduce_sum(y * tf.log(x3))
また、重みやしきい値を計算するためのアルゴリズムには線形回帰分析の例と同じく最急降下法を使用する。
optimizer = tf.train.GradientDescentOptimizer(0.01) minimize = optimizer.minimize(cross_entropy)
データの読み込み
データの読み込み部分のコードは次のようになる。基本的な流れは線形回帰分析の例と同じだが、tf.train.string_input_producer()の引数に2つのファイルを指定することで、1つ目のファイル(digits_data.csv)の読み出しが完了したら続けて2つ目のファイル(test_data.csv)が読み込まれるようにしている。
## データセットを読み込むためのパイプラインを作成する
# リーダーオブジェクトを作成する
reader = tf.TextLineReader()
# 読み込む対象のファイルを格納したキューを作成する
file_queue = tf.train.string_input_producer(["digits_data.csv", "test_data.csv"])
# キューからデータを読み込む
key, value = reader.read(file_queue)
# 読み込んだCSV型式データをデコードする
# [[] for i in range(16)] は
# [[], [], [], [], [], [], [], [],
# [], [], [], [], [], [], [], []]に相当
data = tf.decode_csv(value, record_defaults=[[] for i in range(16)])
# 10件ずつデータを読み出す
# 第1カラム(data[0])はその入力が示す数字だが、
# ニューラルネットワークの出力は10要素の1次元テンソルとなる。
# そのため、10×10の対角行列を作成し、そのdata[0]行目を取り出す操作を行うことで
# 1次元テンソルに変換する。dataは浮動小数点小数型なので、このとき
# int32型にキャストして使用する
data_x, data_y = tf.train.batch([
tf.stack(data[1:]),
tf.reshape(tf.slice(tf.eye(10), [tf.cast(data[0], tf.int32), 0], [1, 10]), [10])
], 10)
# セッションの作成
sess = tf.Session()
# 変数の初期化を実行する
sess.run(tf.global_variables_initializer())
# コーディネータの作成
coord = tf.train.Coordinator()
# キューの開始
threads = tf.train.start_queue_runners(sess=sess, coord=coord)
# ファイルからのデータの読み出し
# 1回目のデータ読み込み。1つ目のファイルから10件のデータが読み込まれる
# 1つ目のファイルには10件のデータがあるので、これで全データが読み込まれる
dataset_x, dataset_y = sess.run([data_x, data_y])
# 2回目のデータ読み込み。1つ目のファイルのデータはすべて読み出したので、
# 続けて2つ目のファイルから読み込みが行われる。
testdata_x, testdata_y = sess.run([data_x, data_y])
以上でモデルの定義、最適化アルゴリズムの定義、データ読み込みが完了したので、学習を実行する。ここでは1万回の反復を行い、100回ごとに交差エントロピーを出力させている。
# 学習を開始
for i in range(100):
for j in range(100):
sess.run(minimize, {x1: dataset_x, y: dataset_y})
print("CROSS ENTROPY:", sess.run(cross_entropy, {x1: dataset_x, y: dataset_y}))
# キューの終了
coord.request_stop()
coord.join(threads)
1万回の反復処理が完了したら、学習に使用したデータとテスト用のデータをそれぞれニューラルネットワークに入力し、その結果を表示する。ここでは、結果を出力するためにいくつかの計算グラフを定義している。
まず、ニューラルネットワークの出力のうち、もっとも値が大きいもののインデックスがニューラルネットワークによって認識された数字となる。これは、入力されたテンソルの各要素を調べ、最も大きい値が格納されているインデックスを出力するtf.argmax()メソッドを使用することで得ることができる。また、指定された2つの引数を比較し、一致していればtrueを返すtf.equal()メソッドを使ってこれを正答(y_value)と比較し、結果をcorrect変数に格納している。この結果correct変数の各要素には、それに対応する入力から得られた出力と期待される値が一致すれば1、そうでなければ0が格納される。
y_value = tf.placeholder(dtype=tf.int64) correct = tf.equal(tf.argmax(x3,1), y_value)
そして、平均値を求めるtf.reduce_mean()メソッドを使ってその結果をaccuracy変数に格納している。
accuracy = tf.reduce_mean(tf.cast(correct, "float"))
あとはこの計算グラフを実行し、その結果を出力すれば良い。
# 学習に使用したデータを入力した場合の
# ニューラルネットワークの出力を表示
print("----result----")
print("raw output:")
print(sess.run(x3,feed_dict={x1: dataset_x}))
print("answers:", sess.run(tf.argmax(x3, 1), feed_dict={x1: dataset_x}))
# このときの正答率を出力
print("accuracy:", sess.run(accuracy, feed_dict={x1: dataset_x, y_value: values_y}))
# テスト用データを入力した場合の
# ニューラルネットワークの出力を表示
print("----test----")
print("raw output:")
print(sess.run(x3,feed_dict={x1: testdata_x}))
print("answers:", sess.run(tf.argmax(x3, 1), feed_dict={x1: testdata_x}))
# このときの正答率を出力
print("accuracy:", sess.run(accuracy, feed_dict={x1: testdata_x, y_value: testvalues_y}))
このコードを実行すると、次のような結果が得られる。
(tensorflow)[hylom@localhost neural2]$ python neural2.py
2017-12-18 23:23:12.087531: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.1 SSE4.2 AVX
CROSS ENTROPY: 22.8904
CROSS ENTROPY: 22.5683
:
:
CROSS ENTROPY: 0.116918
CROSS ENTROPY: 0.115264
----result----
raw output:
[[ 9.89305258e-01 3.48086786e-07 9.78920027e-04 2.49647910e-05
2.13613166e-05 2.06840468e-07 2.41131074e-05 1.23194186e-04
9.28282831e-03 2.38813824e-04]
[ 2.94680174e-08 9.96034682e-01 6.61908824e-04 1.40104117e-03
8.57159478e-07 1.46419811e-03 2.76955048e-04 1.52372129e-04
1.58756393e-06 6.36128152e-06]
[ 3.44952277e-04 4.14907525e-04 9.93275166e-01 2.43327580e-03
3.21461130e-07 1.09102496e-06 1.76503940e-03 8.09512421e-05
1.68369443e-03 6.47618492e-07]
[ 9.91601883e-06 1.52321102e-03 1.81644573e-03 9.87996638e-01
6.80497978e-05 1.99604576e-04 1.05434583e-06 2.67369067e-03
6.19375423e-05 5.64947119e-03]
[ 1.00315929e-05 8.65341553e-06 2.76658767e-07 4.42210803e-05
9.94412005e-01 5.60278204e-05 8.36801135e-08 1.32524222e-03
4.93831118e-04 3.64963012e-03]
[ 5.46079832e-07 6.65704429e-04 1.50655223e-05 4.78135044e-04
2.38829714e-04 9.85909641e-01 6.43138448e-03 1.46542016e-06
3.30118201e-04 5.92919067e-03]
[ 6.85097484e-06 1.59843621e-04 1.16553239e-03 1.18100670e-05
5.09733354e-06 6.25634426e-03 9.85670149e-01 1.24493980e-07
6.70839753e-03 1.58877265e-05]
[ 1.51459977e-03 1.38651289e-04 6.57034980e-05 2.40329397e-03
9.34386451e-04 9.27556627e-08 7.35047023e-10 9.94822860e-01
3.79101220e-06 1.16636460e-04]
[ 9.02480353e-03 1.94091062e-05 2.25256197e-03 1.51166416e-04
3.27065150e-04 8.64764734e-05 5.76172397e-03 2.58601904e-05
9.77574408e-01 4.77657281e-03]
[ 4.52210297e-05 5.11556209e-05 5.81775521e-06 5.73801342e-03
2.98693031e-03 5.99237392e-03 9.15621149e-06 7.70450715e-05
4.51842602e-03 9.80575860e-01]]
answers: [0 1 2 3 4 5 6 7 8 9]
accuracy: 1.0
----test----
raw output:
[[ 9.38309610e-01 2.68126951e-06 4.50509688e-04 1.07168262e-05
1.27424864e-04 1.42898375e-06 1.44315854e-04 2.24396237e-04
5.91430999e-02 1.58574653e-03]
[ 7.18060434e-02 1.83268367e-05 2.53646099e-03 3.83009683e-06
3.96678050e-04 1.01415045e-03 5.14905870e-01 9.19274498e-06
4.08872277e-01 4.37148061e-04]
[ 1.34058250e-03 1.59970801e-02 5.00211790e-02 6.74580514e-01
3.25707770e-05 1.16575666e-05 1.46798277e-06 2.57541865e-01
2.60613433e-05 4.46988706e-04]
[ 3.07822702e-05 2.43430231e-02 2.73652817e-03 8.98540020e-01
1.27675390e-04 3.05516971e-03 2.77303861e-05 5.80019830e-03
6.95849536e-04 6.46428764e-02]
[ 2.99746716e-05 1.68535436e-04 1.59192689e-06 4.56232636e-04
9.37456250e-01 7.73597567e-04 7.52728511e-07 5.11147594e-03
2.35828198e-03 5.36433458e-02]
[ 1.20298557e-06 4.73243184e-04 2.07929916e-05 3.84590268e-04
1.74728164e-04 9.76833880e-01 1.21743660e-02 8.31870409e-07
7.68368947e-04 9.16798413e-03]
[ 5.66605468e-06 1.22323021e-04 1.03206956e-03 1.62812339e-05
2.15192540e-06 6.00737100e-03 9.86170053e-01 5.31856941e-08
6.61445176e-03 2.94541624e-05]
[ 1.07661299e-01 6.10275427e-04 6.98183489e-04 1.20380325e-02
1.59844067e-02 8.75887690e-06 2.14941011e-07 8.36410761e-01
1.13241281e-03 2.54557319e-02]
[ 3.76990647e-03 2.06009674e-04 6.37627614e-04 3.91925241e-05
1.53088651e-03 6.40906655e-05 3.18452553e-03 1.30789718e-04
9.84003246e-01 6.43367274e-03]
[ 3.18376733e-05 1.37926705e-04 4.87122907e-06 4.25673742e-03
1.23894424e-03 4.51130932e-03 8.75021942e-06 9.40964164e-05
3.80500942e-03 9.85910535e-01]]
answers: [0 6 3 3 4 5 6 7 8 9]
accuracy: 0.8
ここでは、学習に使用したデータについては100%の精度、別のテストデータでは80%の精度で文字を認識できていることが分かる。
3層ニューラルネットワークの限界
学習されたシステムを使った結果では、今回のテストデータに対する認識精度は80%となった。この数字だけみると悪くないようにも見えるが、「1」の例のように、2次元的には似た形でも、ニューラルネットワークに入力するデータが大きく変わるようなケースではうまく認識ができていない。
また、最初に定義した乱数の種を変更して重みやしきい値の初期値を変更すると、テストデータの認識率も大きく変わってしまう。このように、単純に3層のニューラルネットを利用するだけでは、正答率はあまり高くすることができない。これが、ニューラルネットの研究が一時停滞した原因でもある。しかし、前回述べたとおりこの問題は4層以上のニューラルネットワークを使った深層学習で解決することができる。次回は、そういった4層以上のニューラルネットワークの利用について解説する。