Numeración egipcia

Para escribir un número ordinal, los egipcios utilizaron tres formas diferentes:

Indicaban el número ordinal: primero, mediante el jeroglífico tpy

Para escribir los números ordinales: segundo a noveno, usaban los números cardinales, añadiendo el sufijo nu:

Los números ordinales décimo en adelante, se indicaban mediante el participio del verbo llenar: mḥt

En contra de lo que pueda parecer, la escritura jeroglífica de los números apenas fue empleada en la vida diaria. La mayor parte de los textos administrativos y contables estaban escritos en papiro o en ostraca en vez de grabarse en piedra y eran textos de numerales escritos en hierático desde el periodo arcaico. Los papiros de Abusir, datados durante el Imperio Antiguo de Egipto, son un conjunto importante de textos que utilizan numerales hieráticos.

La notación hierática emplea un sistema numérico diferente, utilizando signos para los números del 1 al 9, para decenas (múltiplos de diez, del 10 al 90), centenas (del 100 al 900) y millares (del mil al nueve mil). Un número grande, como 9999, se podría escribir empleando este sistema con solo cuatro signos, combinando los signos de 9000, 900, 90 y 9, en vez de usar los 36 jeroglíficos.

Esta diferencia es más aparente que real ya que estos «signos individuales» eran realmente simples ligaduras. En los más antiguos textos hieráticos los números individuales están escritos de forma clara, pero durante el Imperio Antiguo se desarrollaba una serie de escrituras para grupos de signos que contuvieran más de un numeral. Como la escritura hierática seguía desarrollándose con el tiempo, estos grupos de signos se simplificaron para agilizar la escritura, hasta llegar a la escritura demótica. De cualquier forma, es incorrecto hablar de estas ligaduras como un sistema numérico distinto, como sería también incorrecto hablar de un diferente alfabeto comparando textos jeroglíficos con ligaduras hieráticas, ya que estos «signos individuales» eran realmente simples ligaduras. Desde el tercer milenio a. C. los egipcios usaron un sistema de escribir los números en base diez utilizando los jeroglíficos para representar los distintos órdenes de unidades.

Se usaban tantos de cada uno cómo fuera necesario y se podían escribir indistintamente de izquierda a derecha, al revés o de arriba abajo, cambiando la orientación de las figuras según el caso. Al ser indiferente el orden se escribían a veces según criterios estéticos, y solían ir acompañados de los jeroglíficos correspondientes al tipo de objeto (animales, prisioneros, vasijas etc.) cuyo número indicaban.

Estos signos fueron utilizados hasta la incorporación de Egipto al imperio romano. Pero su uso quedó reservado a las inscripciones monumentales, en el uso diario fue sustituido por la escritura hierática y demótica, formas más simples que permitían mayor rapidez y comodidad a los escribas.

Dos de los papiros más conocidos en escritura hierática son el Papiro matemático de Moscú y el Papiro Rhind.

Operaciones elementales con cifras egipcias

Para puntear los signos menos (-) y más (+) se usaban los jeroglíficos: 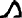o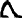

Si los pies estaban orientados en dirección de la escritura significaba suma, al contrario resta.

Los números racionales también podían ser expresados, pero solo como sumas de fracciones unitarias, con la unidad por numerador, excepto para 2/3 y 3/4. El indicativo de fracción es representado por el jeroglífico de la «boca» (j), y significa "parte":

Las fracciones se escribían con este operador, p.e. el numerador 1, y el denominador positivo debajo. Así, 1/3 se escribía:

${\displaystyle ={\frac {1}{3}}}$

Había signos especiales para 1/2, para 2/3 (de uso frecuente) y 3/4 (de uso menos frecuente):

${\displaystyle ={\frac {1}{2}}}$

${\displaystyle ={\frac {2}{3}}}$

${\displaystyle ={\frac {3}{4}}}$

Si el "denominador" era muy grande y el signo de la "boca" no cabía encima, esta se situaba justo encima del comienzo del "denominador".

Aparte de 2/3 y 3/4 los egipcios no conocían fracciones con numerador distinto a uno. Por ejemplo, la fracción 3/5 se representaba como 1/2 + 1/10 y similar a este ejemplo se descomponían todas las fracciones como suma de fracciones con la unidad como numerador.

${\displaystyle ={\frac {1}{331}}}$

• Matemáticas en el Antiguo Egipto
• Sistema de numeración
• Cultura del Antiguo Egipto

• Numerales en jeroglificos.es
• Introduction (Introducción)
• O'Connor, John J.; Robertson, Edmund F., «Egyptian numerals» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, https://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_numerals/ .
• Numbers and dates (Números y fechas)
• Hieratic numerals (Numerales hieráticos)