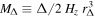Abstract
The inner slope (γDM) of the dark matter (DM) density profile of cosmological halos carries information about the properties of DM and/or baryonic processes affecting the halo gravitational potential. Cold DM cosmological simulations predict steep inner slopes, γDM ≃ 1. We test this prediction on the MACS J1206.2-0847 cluster at redshift z = 0.44, whose DM density profile has been claimed to be cored at the center. We determine the cluster DM density profile from 2 kpc from the cluster center to the virial radius (∼2 Mpc), using the velocity distribution of ≃500 cluster galaxies and the internal velocity dispersion profile of the Brightest Cluster Galaxy (BCG), obtained from VIMOS@VLT and MUSE@VLT data. We solve the Jeans equation of dynamical equilibrium using an upgraded version of the MAMPOSSt method. The total mass profile is modeled as a sum of a generalized Navarro–Frenk–White profile that describes the DM component, allowing for a free inner slope of the density profile, a Jaffe profile that describes the BCG stellar mass component, and a nonparametric baryonic profile that describes the sum of the remaining galaxy stellar mass and of the hot intra-cluster gas mass. Our total mass profile is in remarkable agreement with independent determinations based on X-ray observations and strong lensing. We find 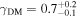 (68% confidence levels), consistent with predictions from recent Lambda cold dark matter cosmological numerical simulations.
(68% confidence levels), consistent with predictions from recent Lambda cold dark matter cosmological numerical simulations.
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Investigating the mass distribution of cosmological halos is important to understand the halo assembly process through the interplay of dark matter (DM) and baryons (e.g., Blumenthal et al. 1986; El-Zant et al. 2001; Lackner & Ostriker 2010; Correa et al. 2015a), and to constrain the properties of DM itself and of gravitational interactions (e.g., Arabadjis et al. 2002; Markevitch et al. 2004; Sartoris et al. 2014; Pizzuti et al. 2022). Cold DM-only cosmological simulations find that DM halo mass density profiles follow the universal Navarro–Frenk–White (NFW) model,
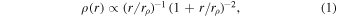
over a wide range of halo masses, from the center to the virial radius (Navarro et al. 1996, 1997). The logarithmic slope of the NFW model changes from  at r = 0, to 3 at large radii, and its characteristic radius, rρ
, corresponds to the radius r2 where γDM = 2.
at r = 0, to 3 at large radii, and its characteristic radius, rρ
, corresponds to the radius r2 where γDM = 2.
In the following studies, based on simulations with higher resolution than the original one by Navarro et al. (1996), the universality of halo ρ(r) has been questioned (e.g., Ricotti et al. 2007; Del Popolo 2010), and a generalized form of the initial NFW model (gNFW hereafter) has been proposed by Wyithe et al. (2001),
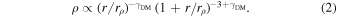
In this case, rρ ≡ r2/(2 − γDM). The gNFW model allows a free value of the inner slope of the halo DM profile, γDM. Based on the recent C-EAGLE hydrodynamic simulations (Barnes et al. 2017), He et al. (2020) constrain the average inner slope of the DM density profile of cluster-size halos, and its scatter, finding γDM = 1.07 ± 0.06.
The inner slope γDM of halo ρ(r) can depend on the nature of DM. Numerical simulations have shown that there are several alternative models to the cold dark matter (CDM) scenario, such as warm, fuzzy, decaying, and self-interacting DM, that can produce halos with γDM < 1 (Hu et al. 2000; Spergel & Steinhardt 2000; Bode et al. 2001; Peter et al. 2010). Self-interacting DM halo profiles, in particular, are well fit by cored isothermal profiles (Robertson et al. 2021).
The inner structure of halos and the value of γDM can also differ from the predictions of CDM-only simulations because of collisional processes that concern the baryonic components. In particular, γDM > 1 can result from the process of adiabatic contraction caused by the central condensation of cooled gas, and from the process of mass accretion (Blumenthal et al. 1986; Gnedin et al. 2004; Laporte et al. 2012; Diemer & Kravtsov 2014; Schaller et al. 2015). On the other hand, the processes of dynamical friction and active galactic nuclei (AGN) feedback can flatten the central slope of the DM profile (γDM < 1, El-Zant et al. 2001, 2004; Martizzi et al. 2012; Ragone-Figueroa et al. 2012; Peirani et al. 2017).
Clusters of galaxies are particularly well suited for the study of the DM density profiles, since their mass budget is dominated by DM at most radii (see, e.g., Biviano & Salucci 2006), at variance with galaxies whose mass profile at the center is dominated by baryons (Robertson et al. 2021). The cluster mass profile can be constrained through X-ray and Sunyaev–Zel'dovich (Sunyaev & Zeldovich 1969) observations of the hot intra-cluster medium (ICM), weak gravitational lensing, and the kinematics of cluster galaxies (e.g., Pratt et al. 2019). The best probes of the cluster gravitational potential close to its center are strong gravitational lensing (e.g., Mellier et al. 1993; Zitrin et al. 2012) and the internal kinematics of the brightest cluster galaxy (BCG; see, e.g., Dressler 1979; Kelson et al. 2002). The output of all these measurements is the cluster total mass profile, to which one must subtract the contribution of baryons to extract the DM profile. Most baryons outside the very cluster center are contributed by the ICM, while the BCG stellar mass dominates the baryon budget close to the center, where it makes a non-negligible, and in some cases dominant, contribution to the total mass budget (see, e.g., Biviano & Salucci 2006). Therefore, measuring the BCG stellar mass profile is fundamental to obtaining a reliable estimate of γDM.
Previous observational determinations of γDM for clusters of galaxies span a wide range of values. Kelson et al. (2002) studied the dynamics of the cluster A2199 by combining the kinematics of the BCG and intra-cluster light stars with that of the cluster members, while assuming isotropic velocity distributions. They found that a cored DM halo reproduces the observed kinematics better than an NFW profile. Based on a strong lensing analysis of three clusters, Limousin et al. (2022) find that cored inner mass density profiles are favored over cuspy models. Using a combination of strong gravitational lensing and BCG kinematics, Newman et al. (2013b) estimate γDM = 0.50 ± 0.13 averaging over seven clusters, in agreement with previous results by the same collaboration (Sand et al. 2002, 2008; Newman et al. 2009, 2011). All seven clusters, and another two from a previous investigation (Sand et al. 2004, hereafter S04), have γDM < 1 with various levels of statistical confidence. A larger value is found by Annunziatella et al. (2017), who estimate γDM = 1.36 ± 0.01 for the cluster MACS J0416-2403, based on BCG kinematics, X-ray, and strong lensing. However, their estimate is based on the assumption of a single power-law mass profile for de-projection, and this assumption could lead to an overestimate of γDM if the intrinsic 3D mass profile steepens with radius, as expected for clusters of galaxies. By combining the BCG with the cluster kinematics (as traced by its member galaxies), Sartoris et al. (2020) find γDM = 0.99 ± 0.04 for the cluster Abell S1063.
The mass profile inner slope of the cluster MACS J1206.2-0847 (MACS 1206 hereafter), has been determined by five different studies. Umetsu et al. (2012), Caminha et al. (2017), and Young et al. (2015) have determined the inner slope of the total mass density profile, γtot, the first two based on strong lensing, and the latter based on the Sunyaev–Zel'dovich emission. The strong lensing analyses found γtot ≈ 0.9–1.0, while the analysis of Young et al. (2015) found a smaller value, 0.7 (no error bars provided). S04 and Manjón-García et al. (2020) have determined γDM based on strong lensing, in combination with the internal kinematics of the BCG in the case of S04. Of the two values, one is given without an error estimate (Manjón-García et al. 2020) and the other is zero, and significantly smaller than the NFW value (S04). The result of S04 is supported by the strong lensing analysis of Limousin et al. (2022), who find that a cored inner mass density profile is a better fit to the data than a cuspy model.
Given the rather extreme γDM value measured for MACS 1206 by S04, and supported by the analysis of Limousin et al. (2022), it is interesting to have a new, independent determination of it with a kinematic data set of superior quality. In this paper, we apply the procedure of Sartoris et al. (2020) to our new data for the cluster galaxy redshifts and the BCG velocity dispersion profile, that come from the CLASH-VLT ESO Large Program (D 186.A-0798, P.I. P. Rosati, Rosati et al. 2014) and from additional archival observations obtained with the integral field spectrograph MUSE@VLT (Caminha et al. 2017).
The structure of this paper is the following. In Sections 2 and 3, we describe our data set, and the method of analysis, respectively. We provide our results in Section 4 with the relevant discussion in Section 5. In Section 6, we provide a summary of our results and our conclusions. Throughout this paper, we adopt the following cosmological parameters: Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1. At the cluster redshift, z = 0.44, 1' corresponds to 340 kpc.
2. Data Set
Our data set consists of 3110 sources with measured redshift, 2650 obtained with VIMOS@VLT within the CLASH-VLT ESO Large Program (D 186.A-0798, P.I. P. Rosati, Rosati et al. 2014), 410 obtained with MUSE@VLT (Caminha et al. 2017), 15 14 observed with FORS@VLT (Presotto et al. 2014), 11 observed with IMACS-GISMO at the Magellan telescope (Daniel Kelson, private communiction) and another 25 gathered from the literature (Jones et al. 2004; Lamareille et al. 2006; Ebeling et al. 2009). Details of the construction of the spectroscopic catalog can be found in Balestra et al. (2016). The uncertainties in the redshift measurements correspond to uncertainties in the rest-frame velocities of cluster galaxies of 153, 75, and 15 km s−1 for the measurements obtained with VIMOS-LR, VIMOS-MR, and MUSE, respectively. In addition, we have obtained very accurate MUSE measurements of the surface brightness and velocity dispersion profiles of the BCG.
2.1. Selection of Cluster Members
We adopt the BCG position as the cluster center, both in spatial coordinates,  , and in redshift, z = 0.4398. The BCG position is within 13 kpc of the X-ray peak position and the center of mass is determined by the gravitational lensing analysis (Umetsu et al. 2012). We considered three independent techniques for the selection of cluster members based on their location in the cluster projected phase space:
, and in redshift, z = 0.4398. The BCG position is within 13 kpc of the X-ray peak position and the center of mass is determined by the gravitational lensing analysis (Umetsu et al. 2012). We considered three independent techniques for the selection of cluster members based on their location in the cluster projected phase space:
- 1.CLUMPS, based on the identification of peaks in the velocity distribution of galaxies as a function of the cluster-centric distance (see Biviano et al. 2021, for a full description of the method);
- 2.
- 3.Clean, based on the estimate of the line-of-sight velocity dispersion profile resulting from assuming an NFW mass density profile and a given velocity anisotropy profile (see Mamon et al. 2013, for a full description of the method).
As explained in Section 3, we restrict our dynamical analysis to radii R ≤ 2.2 Mpc, which excludes the galaxies (1842 in total) shown in the gray region in Figure 1. In this inner region, CLUMPS, P + G, and Clean identify 476, 485, and 482 member galaxies, respectively. In the following, we compare the CLUMPS and P + G samples, while we do not consider the Clean sample because it is intermediate between the two. The distribution of galaxies in the cluster projected phase space and their spatial distribution are shown in Figures 1 and 2, respectively. In both figures, we distinguish interlopers and cluster members selected by CLUMPS and P+G.
Figure 1. Rest-frame line-of-sight velocity (kilometers per second) vs. projected cluster-centric distance (kiloparsec) of galaxies in the cluster region. Red squares indicate members selected by the CLUMPS method alone (seven galaxies), blue stars indicate members selected by the P+G method alone (31 galaxies), green dots indicate members selected by both P+G and CLUMPS (680 galaxies), and magenta crosses indicate galaxies that are not selected as members by either of the two methods (2392 galaxies). The black vertical dashed line indicates the value of the virial radius, 1.96 Mpc, according to Umetsu et al. (2012). Galaxies in the gray regions are excluded from the dynamical analysis (see Section 3). The pink region within dotted segments is the region of the phase space occupied by a likely foreground group of galaxies (discussed in Section 4 and previously identified by Young et al. 2015).
Download figure:
Standard image High-resolution imageFigure 2. Spatial distribution of member and nonmember galaxies shown in the projected phase-space diagram of Figure 1, with the same symbols and colors (all other spectroscopic galaxies in the field are not shown). The dashed red circle represents the virial radius, while the white area includes galaxies used for the dynamical analysis. The inset is a blow-up of the central megaparsec, where the pink open boxes mark the galaxies in the foreground group (see the pink region in Figure 1).
Download figure:
Standard image High-resolution imageThe difference in the number of selected members between the CLUMPS and P+G methods is <2%, mostly due to a few galaxies at small projected distances and relatively large negative line-of-sight velocities from the cluster center. We used the Kernel Mixture Modeling (KMM) algorithm (McLachlan & Basford 1988; Ashman et al. 1994) to check for bimodality in the velocity distributions of the two samples of members, as a possible indication of the presence of a group of galaxies in the foreground or background of the cluster. Only for the P + G sample, we found significant evidence for bimodality. The 12 galaxies near the cluster center that P + G identifies as members and CLUMPS does not (blue stars within the pink region in Figure 1) are assigned by KMM a probability of 90% belonging to a different group than the main cluster. In Section 4, we provide additional evidence that these galaxies are indeed members of a foreground group, that was previously identified by Young et al. (2015).
Given the KMM results, we consider the CLUMPS sample of members our reference sample on which we perform our dynamical analysis. We also perform the same dynamical analysis on the P+G sample of members to assess the impact of a different member selection on our results.
2.2. BCG
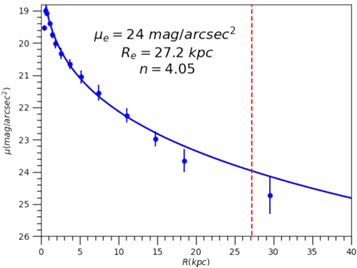
We fitted the BCG surface brightness profile in the I band with a Sérsic model (Sérsic 1963), by using GALFIT (Peng et al. 2011) and the procedure described in Tortorelli & Mercurio (2023). The cluster region where the BCG is located is a crowded environment, and it is characterized by the presence of the intra-cluster light. For these reasons, to obtain a robust fit of the 2D galaxy surface brightness of the BCG, we used the methodology described in Tortorelli et al. (2018) and Tortorelli & Mercurio (2023). This is based on an iterative approach that analyzes images of increasing size (to deal with nearest neighbors) and on multiple background estimation (to deal with the intra-cluster light flux contamination). All the pixels belonging to the BCG image, with a flux above the measured background, were considered in the Sérsic fit. We found the best fit with an index n = 4.05, an effective radius Re = 27.2 kpc, and a total luminosity LBCG = 4.92 × 1011 L⊙. We show in Figure 3 that the aperture magnitudes centered on the galaxy are very well reproduced by the Sérsic profile computed with the best-fitting structural parameters. To measure aperture magnitudes we did not correct for the point-spread-function, and this is the reason why the first point in Figure 3 is lower than the value expected from the best-fit Sérsic model and we used a radial range less extended than the region fitted to obtain the 2D surface brightness profile. The Sérsic index is very close to n = 4, corresponding to a de Vaucouleurs profile (de Vaucouleurs 1948). This is very convenient since the de-projection of the de Vaucouleurs profile is well approximated by the Jaffe profile (Jaffe 1983),
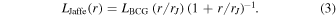
where rJ = Re /0.763.
Figure 3. Best-fit Sérsic profile (solid blue line) to the BCG obtained by using galfit (see the text). Blue points represent the surface brightnesses obtained measuring aperture magnitudes, without applying corrections for the point-spread function to guide the eye for the fit. The vertical dashed red line shows the position of the effective radius, Re = 27.2 kpc.
Download figure:
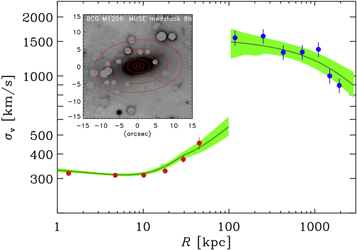
Standard image High-resolution imageThe velocity dispersion profile of the BCG has been obtained from MUSE observations (see Figure 4), by adopting the methodology described in Sartoris et al. (2020). We extracted spectra of the BCG in elliptical radial bins from the MUSE data cube, by masking out several interloper galaxies (see the light-gray filled circles in the inset of Figure 4). The spatial resolution is limited by the seeing of 06 (see Caminha et al. (2017), sampled with 0
2 pixels), while the velocity resolution is ∼10 km s−1 for high signal-to-noise ratio (S/N) spectra. The stellar line-of-sight velocity dispersion in each bin is then measured with the pPXF public software (Cappellari 2017), adopting the same setup parameters and stellar library as in Sartoris et al. (2020). The precision and accuracy of pPXF in measuring velocity dispersions in different S/N regimes are discussed and tested in Bergamini et al. (2019). The six elliptical annuli shown in Figure 4 correspond to radial bins along the semimajor axis, with a = [0.0–0.6, 0.6–1.5, 1.5–3.0, 3.0–5.0, 5.0–8.0, 8.0–12.0] arcseconds. The ellipses follow the BCG light with a rotation angle of 185° and axes ratio of a/b = 1.6. The circularized radius of each bin is the midpoint of each annulus with equal area, i.e.,
 . Thanks to the 8.5 hr long exposure of the MUSE observations, the mean S/N of the spectra extracted in each bin ranges from 90–100, for the two central bins (R = 1.35, 4.72 kpc), to 21 and 11 for the two outer bins (R = 29.2, 44.9 kpc), respectively. The pPXF cross-correlation procedure not only provides the velocity dispersion in each bin but also the mean velocity, for which we found a scatter of a few kilometers per second, revealing no significant rotational support for the BCG.
. Thanks to the 8.5 hr long exposure of the MUSE observations, the mean S/N of the spectra extracted in each bin ranges from 90–100, for the two central bins (R = 1.35, 4.72 kpc), to 21 and 11 for the two outer bins (R = 29.2, 44.9 kpc), respectively. The pPXF cross-correlation procedure not only provides the velocity dispersion in each bin but also the mean velocity, for which we found a scatter of a few kilometers per second, revealing no significant rotational support for the BCG.
Figure 4. Observed line-of-sight velocity dispersion profiles of the BCG (red dots) and of the cluster, as traced by the galaxies (blue dots). Error bars are 1σ. The green curve and shaded regions are the median and 68% c.l. predicted by Model 1 (see Table 1 in Section 4). The inset shows the MUSE image of the BCG with the overlaid elliptical annuli used to measure the internal velocity dispersion out to R ≃ 50 kpc. The light-gray circles are sources masked out in the spectral extraction.
Download figure:
Standard image High-resolution image2.3. Intra-cluster Gas
We estimated the gas mass based on dedicated Chandra ACIS-I exposures (ObsIDs 20544, 209229, 21078, 21079, 21081). We reprocessed them with a standard pipeline based on CIAO 4.10 (Fruscione et al. 2006) and CALDB 4.7.8 to create a new events-2 file which includes filtering for grade, status, bad pixels, and time intervals for anomalous background levels. We obtained a cumulative good time interval of 174.0 ks. All the point sources detected with the CIAO routine wavdetect were masked and not considered in the following analysis. An exposure-corrected image in the 0.7–2 keV band was used to extract a surface brightness profile that was geometrically deprojected (assuming a Galactic absorption nH = 3.7 × 1020 particles cm−2) to recover an electron density profile ne
(r). A local background 94 far from the X-ray peak, and with no contamination from the cluster emission, was used. The gas mass is then
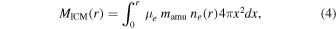
where μe = 1.16 is the mean electron mass weight appropriate for a fully ionized plasma with 30% solar abundances (Asplund et al. 2009), and mamu = 1.66 × 10−24 g is the atomic mass unit.
A full spectral analysis provided the measurements of the gas temperature in azimuthally averaged bins up to ∼800 kpc. By following the backward approach to reconstruct the hydrostatic mass as described in Ettori et al. (2010), we constrained the total mass profile using an NFW model with best-fit parameters 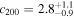 and
and  Mpc.
Mpc.
3. Dynamical Analysis Method
To determine the cluster mass profile we performed a simultaneous maximum likelihood fit to the BCG velocity dispersion profile, and to the velocity distribution of cluster members as a function of radius, out to 2.2 Mpc. This radius corresponds to a 2σ upper limit to the virial radius r200
16
estimate of the cluster from the gravitational lensing analysis of Umetsu et al. (2012). We used an extension of the MAMPOSSt method
17
originally developed by Mamon et al. (2013), which we already used in the dynamical analysis of the AS1063 cluster (Sartoris et al. 2020). In this extension of the original code, MAMPOSSt estimates the likelihood  of the observed projected phase-space distribution of cluster members, and combines this likelihood with the likelihood resulting from the χ2 fit to the observed, line-of-sight BCG stellar velocity dispersion profile, (using Equations (9) and (26) in Mamon et al. 2013). The inputs to MAMPOSStare the individual cluster-centric radial distances and rest-frame velocities of the cluster members (identified as described in Section 2.1), and the surface brightness and velocity dispersion profiles of the BCG in radial concentric bins.
of the observed projected phase-space distribution of cluster members, and combines this likelihood with the likelihood resulting from the χ2 fit to the observed, line-of-sight BCG stellar velocity dispersion profile, (using Equations (9) and (26) in Mamon et al. 2013). The inputs to MAMPOSStare the individual cluster-centric radial distances and rest-frame velocities of the cluster members (identified as described in Section 2.1), and the surface brightness and velocity dispersion profiles of the BCG in radial concentric bins.
The final likelihood of the model is given by the sum 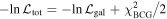 (based on the theorem of Wilks 1938). The following profiles enter the
(based on the theorem of Wilks 1938). The following profiles enter the 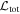 determination:
determination:
- 1.The number density profile of the BCG stars, νBCG(r),
- 2.The number density profile of the cluster members, νgal(r),
- 3.The cluster total mass profile, M(r),
- 4.The velocity anisotropy profile of the BCG stars, βBCG(r),
- 5.The velocity anisotropy profile of the cluster galaxies, βgal(r),
where 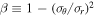 and σθ
and σr
are the tangential and radial components of the velocity dispersion, respectively. In the following, we describe how we modeled these profiles for our dynamical analysis.
and σθ
and σr
are the tangential and radial components of the velocity dispersion, respectively. In the following, we describe how we modeled these profiles for our dynamical analysis.
3.1. Number Density Profiles
We assumed νBCG(r) to coincide with the de-projection of the BCG surface brightness profile, which we approximated with a Jaffe profile (Jaffe 1983, see Equation (3)).
To determine νgal(r) we had to first account for the incompleteness of our spectroscopic data set. What is relevant here is only the relative completeness at different cluster-centric radii. Our MUSE observations are much deeper than our VIMOS observations, but are restricted to a very central region. To reduce the difference in spectroscopic completeness between the region covered by MUSE observations and other regions, and limit the amount of completeness correction, in the determination of νgal(r) we restricted the samples of members to a RC-band magnitude ≤24 that is approximately the limit reached by the non-MUSE redshift determinations. This magnitude cut leaves ∼90% of the members in the full sample (433 and 439 galaxies within 2.2 Mpc in the CLUMPS and P+G samples, respectively), that can be considered representative of the full sample. We estimated the spectroscopic completeness as a function of cluster-centric radii, following the procedure of Biviano et al. (2013). The region covered by MUSE observations is complete to the chosen magnitude limit, while the remaining subsample has a radially decreasing completeness, from a value of ∼0.8 near the center to ∼0.7 at the virial radius.
We used a maximum likelihood technique (Sarazin 1980) to fit a projected NFW model (Bartelmann 1996) to the projected number density profile of cluster members, separately for the CLUMPS and P
+
G samples. In the fitting procedure, we weighted each galaxy by the inverse of its radial completeness. The best fits are shown in Figure 5. There is only one free parameter in the fit, the scale radius rν
of the NFW model, since the normalization of the fitting function is constrained by the requirement that the total (completeness corrected) number of observed galaxies is identical to the integral of the fitting function over the radial range of the fit. By definition, the best-fit rν
values of the projected NFW profiles are the same also for the 3D NFW profiles. We found very similar best-fit values for the CLUMPS and P
+
G sample,  and
and  Mpc, respectively. These values are consistent within 1σ with the estimate of (Biviano et al. 2013,
Mpc, respectively. These values are consistent within 1σ with the estimate of (Biviano et al. 2013, 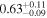 ), albeit slightly smaller, but they did not have MUSE data, they cut the sample one magnitude brighter than we do, and they ignored the 20% change in radial completeness of their sample.
), albeit slightly smaller, but they did not have MUSE data, they cut the sample one magnitude brighter than we do, and they ignored the 20% change in radial completeness of their sample.
Figure 5. The projected number density profiles of cluster members (dots with 1σ error bars), corrected for spectroscopic incompleteness, and their best fits with projected NFW models (lines with 1σ confidence regions). CLUMPS sample: red points, orange line, and yellow confidence region. P + G sample: blue navy points, blue line, and cyan region.
Download figure:
Standard image High-resolution image3.2. Mass Profile
We model the total cluster mass profile as the sum of several components,
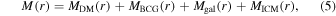
where MDM is the DM profile, while MBCG, Mgal, and MICM are the baryonic mass profiles, namely the BCG stellar mass profile, the stellar mass of all other member galaxies (satellites hereafter), and the mass of the hot intra-cluster gas. We characterize the DM profile by a gNFW model,
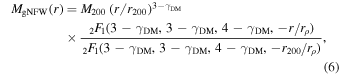
where 2 F1 is the hypergeometric function (Mamon et al. 2019). There are three free parameters in this model, r200, rρ , and γDM. The BCG stellar mass profile is given by MBCG(r) = (M/L) LJaffe(r) (see Equation (3)) and the only free parameter is the mass-to-light ratio (M/L). We take the satellite stellar mass profile Mgal(r) from Annunziatella et al. (2014). The hot intra-cluster gas mass profile MICM(r) is derived as described in Section 2.3. We consider Mgal and MICM as fixed and neglect their uncertainties, since their contribution to the total mass near the cluster center is very marginal (see Figure 6).
Figure 6. Total mass profiles M(r) of the MACS 1206 cluster. Green (gray) shading: 68% confidence region for the total mass profile obtained from the kinematical analysis—Model 1 (respectively, from the X-ray hydrostatic analysis). Blue (respectively, red) solid line: DM profile (respectively, BCG stellar mass profile). Navy blue dashed line: satellites stellar mass profile. Magenta dashed–dotted line: intra-cluster gas mass profile.
Download figure:
Standard image High-resolution image3.3. Velocity Anisotropy Profiles
Kronawitter et al. (2000) found a remarkable homogeneity in the velocity anisotropy profile β(r) of giant ellipticals. The studies of Kronawitter et al. (2000) and Santucci et al. (2023) indicate that giant ellipticals have at most mild velocity anisotropy, β ≲ 0.3. We therefore try two constant β models, namely, β = 0 and β = 0.3 at all radii. To assess the impact of our assumption we also consider a third model, the OM model (Osipkov 1979; Merritt 1985) in which β(r) rises fast with radius,
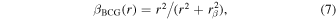
where we assume rβ = rJ .
The velocity dispersion profile of galaxy clusters is less well constrained than that of the BCG, and probably much less homogeneous across different clusters (see, e.g., Wojtak & Łokas 2010; Biviano et al. 2013; Mamon et al. 2013; Munari et al. 2013; Mamon et al. 2019). Lacking strong priors on the cluster β(r) we adopt a very generic model with two free parameters indicating the anisotropy at r = 0, β0, and at large radii, β∞ (Tiret et al. 2007),
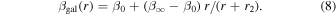
In our analysis, we provide constraints on β0 and β∞ in terms of the equivalent parameters 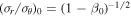 and
and 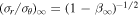 .
.
4. Dynamical Analysis Results
We determine the marginal distributions of the free parameters in the dynamical analysis by a Monte Carlo Markov Chain (MCMC) sampling of 100,000 points in the parameter space. The free parameters in our MAMPOSSt runs are the following:  , plus the rν
parameter for which we assume the ±1σ interval derived externally (see Section 3.1) as a flat prior in the MAMPOSSt runs. We run MAMPOSSt on both our fiducial sample of cluster members, based on the CLUMPS algorithm, and, for comparison, also on our P+G sample of cluster members, using all three BCG velocity anisotropy models described in Section 3.3. In Table 1, we list the median values and 68% c.l. of all parameters, for the CLUMPS sample and the three βBCG models (numbered 1–3 in the table), as well as for the P+G sample with βBCG = 0.0 (Model 4 in the table; we do not show the results for the other BCG anisotropy profiles for the sake of conciseness). The results for Model 1 are displayed in the triangular plot of Figure 7.
, plus the rν
parameter for which we assume the ±1σ interval derived externally (see Section 3.1) as a flat prior in the MAMPOSSt runs. We run MAMPOSSt on both our fiducial sample of cluster members, based on the CLUMPS algorithm, and, for comparison, also on our P+G sample of cluster members, using all three BCG velocity anisotropy models described in Section 3.3. In Table 1, we list the median values and 68% c.l. of all parameters, for the CLUMPS sample and the three βBCG models (numbered 1–3 in the table), as well as for the P+G sample with βBCG = 0.0 (Model 4 in the table; we do not show the results for the other BCG anisotropy profiles for the sake of conciseness). The results for Model 1 are displayed in the triangular plot of Figure 7.
Figure 7. Result of the MAMPOSSt analysis on the CLUMPS sample, using βBCG = 0.0 (Model 1), based on the marginalization of the posterior distribution resulting from the 100,000 samples of the MCMC analysis. The red lines and dots indicate the median of the distribution, The light (respectively, dark) blue regions indicate the 68% (respectively, 95%) c.l. The BCG M/L is relative to the I-band luminosity.
Download figure:
Standard image High-resolution imageTable 1. Results of the MAMPOSSt Analysis
| Model ID | Sample | βBCG | r200 | rρ | γDM | M/L |
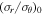
|
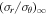
| ΔBIC |
|---|---|---|---|---|---|---|---|---|---|
| (Mpc) | (Mpc) | (M⊙/L⊙) | |||||||
| [68% c.l.] | |||||||||
| [95% c.l.] | |||||||||
| 1 | CLUMPS | 0.0 | 2.00 | 0.87 | 0.73 | 4.48 | 1.65 | 3.19 | 0.9 |
| [1.89–2.10] | [0.48–1.02] | [0.59–0.91] | [4.36–4.63] | [1.20–1.87] | [2.04–4.09] | ||||
| [1.81–2.21] | [0.33–1.60] | [0.39–1.04] | [4.20–4.74] | [1.00–2.48] | [1.59–4.91] | ||||
| 2 | CLUMPS | 0.3 | 1.99 | 1.01 | 0.76 | 3.91 | 1.81 | 3.17 | 0.0 |
| [1.88–2.09] | [0.50–1.20] | [0.61–0.95] | [3.77–4.07] | [1.31–1.98] | [2.10–4.16] | ||||
| [1.79–2.22] | [0.30–2.03] | [0.39–1.10] | [3.59–4.19] | [1.08–2.83] | [1.48–4.92] | ||||
| 3 | CLUMPS | OM | 1.96 | 0.98 | 0.21 | 4.64 | 2.07 | 3.48 | 13.6 |
| [1.84–2.06] | [0.69–1.04] | [0.01–0.28] | [4.56–4.72] | [1.45–2.26] | [2.59–4.53] | ||||
| [1.74–2.19] | [0.59–1.58] | [0.00–0.53] | [4.48–4.79] | [1.24–3.26] | [1.89–5.03] | ||||
| 4 | P+G | 0.0 | 1.97 | 0.83 | 0.71 | 4.49 | 1.60 | 2.91 | 17.9 |
| [1.84–2.08] | [0.44–0.98] | [0.55–0.91] | [4.36–4.64] | [1.16–1.71] | [1.59–3.81] | ||||
| [1.75–2.21] | [0.27–1.67] | [0.33–1.06] | [4.19–4.64] | [0.95–2.44] | [1.15–4.88] | ||||
Note. For each model, we provide in the first row the median values of the parameters from the marginal distribution obtained with the MAMPOSSt analysis, in the second, and respectively, third row, the 68% and 95% c.l. on these parameters. The BCG M/L is relative to the I-band luminosity. The last column gives the value of ΔBIC with respect to the best-fit Model 2 resulting from the comparison between the observed velocity dispersion profiles of the BCG and the cluster and those predicted by the best-fit MAMPOSSt models.
Download table as: ASCIITypeset image
The best-fit parameter values do not depend on the sample, but some of them do depend on the choice of BCG velocity anisotropy models, even if most differences are within the 95% c.l. In particular,
- 1.γDM is higher for the two βBCG constant models (1 and 2 in Table 1) than for Model 3, which uses the OM βBCG(r);
- 2.the I-band BCG M/L is lowest for Model 2 (βBCG = 0.3).
To select among the different models, we evaluate how well they fit the observed line-of-sight velocity dispersion profiles of the BCG and the cluster. We compute the model-predicted velocity dispersion profiles by applying Equations (9) and (26) in Mamon et al. (2013). We then evaluate
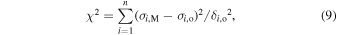
where σi,o and σi,M are, respectively, the observed velocity dispersion and the average of the profiles resulting from the 100,000 parameter samples of the MCMC analysis, and δi,o is the 1σ error on the observed velocity dispersion, all quantities evaluated for the ith of n radial bins. We then use the Bayes information criterion (BIC, Schwarz 1978), to compare the quality of the fits of the different models,  , where k is the number of free parameters and N is the number of data, which is slightly different for Model 4 and the other models. the ΔBIC values are listed in Table 1 with respect to the minimum value of χ2 among the four models.
, where k is the number of free parameters and N is the number of data, which is slightly different for Model 4 and the other models. the ΔBIC values are listed in Table 1 with respect to the minimum value of χ2 among the four models.
According to Kass & Rafferty (1995), a value ΔBIC > 10 indicates strong evidence against the model with the largest BIC, while a value ΔBIC < 2 does not indicate a significant difference in the quality of the fits of the two models compared. We then conclude that the βBCG = 0.0 Model 1 and βBCG = 0.3 Model 2 provide an equally good fit to the data, and a significantly better fit than the OM βBCG Model 3, for both the CLUMPS and P+G samples. The fits obtained using the P+G sample are significantly worse than those obtained using the CLUMPS sample. This is due to the inclusion of a probable foreground group of galaxies in the P+G sample of members, which increases the line-of-sight velocity dispersion of the cluster near the center (see Figure 1). Given the results of the χ2 analysis, in the following, we only consider Models 1 and 2, both based on the CLUMPS sample.
Since there is tension in the value of the M/L parameter obtained by using the βBCG = 0.0 and 0.3 Models 1 and 2, we look for external constraints on M/L. Conroy & van Dokkum (2012) estimated the M/L of 38 ellipticals using stellar population synthesis models based on a variable initial mass function. They found that the velocity dispersion of low-z early-type galaxies correlates with their M/L. Using the data of Table 2 in their paper, we fit the relation M/L = −0.4 + 1.6 σBCG, where the BCG luminosity is observed in the I band, and σBCG is the observed BCG velocity dispersion in units of 100 km s−1, measured within an aperture of Re /8. To apply this relation to the BCG of MACS 1206, we apply the evolutionary and K-corrections to the I-band magnitude of our BCG, using the tables of Poggianti (1997), updated for the cosmology used in this paper. We find that the two corrections almost cancel out, giving a ∼4% difference in luminosity that we ignore in this consideration. The MACS 1206 BCG has σ = 315 km s−1 within the radius Re /8 = 3.4 kpc, which would indicate M/L = 4.6 M⊙/L⊙. This value is marginally closer to the solution we found for the βBCG = 0.0 Model 1, which we therefore consider our reference model for the following discussion. Our Model 1 dynamically derived M/L value supports Conroy & van Dokkum (2012)'s conclusion of a bottom-heavy IMF for high-velocity dispersion ellipticals.
The predicted BCG and cluster velocity dispersion profiles for Model 1 are compared to the observed profiles in Figure 4. Note that the BCG velocity dispersion profile does not join onto that of the cluster galaxies, and this is mostly due to the fact that the BCG stars and galaxies do not follow the same spatial distribution (i.e., the BCG and galaxies ν(r) in Equation (9) of Mamon et al. 2013, are different), and partly due to their different orbital distributions. Overall, the fit appears very good, although the formal value of the χ2 is rather high, 30.8 for 14 data points and seven free parameters (it is only slightly smaller for Model 2), due to the very small error bars of the velocity dispersion profile of the BCG.
In summary, Model 1 is characterized by a M(r) with a DM inner slope slightly shallower than the NFW profile, isotropic stellar orbits of the BCG, and radially elongated orbits of the cluster galaxies, with increasing anisotropy at larger radii. The increasing anisotropy with radius is a feature seen in cluster-size halos from cosmological simulations (see, e.g., Munari et al. 2013; Lotz et al. 2019), and also found by Biviano et al. (2013) for the same cluster, but Model 1 predicts a stronger radial anisotropy, especially near the center, although the difference is less than 95% significant. The total M(r) of Model 1 and its components are shown in Figure 6.
In Figure 6 we also show the total M(r) obtained by the X-ray hydrostatic analysis (see Section 2.3). This M(r) is consistent with the M(r) we obtain from kinematics at radii ≳300 kpc, but lies above it at smaller radii. The difference can be attributed to the fact that we adopted the NFW model in the X-ray analysis, since the X-ray data alone do not allow constraining the inner slope of a more generic gNFW model. Cluster masses derived from X-ray data are often claimed to be affected by the so-called hydrostatic bias (e.g., Rasia et al. 2006; Lau et al. 2009; Hoekstra et al. 2015). Our analysis does not show significant evidence of the hydrostatic bias in this cluster, in agreement with our previous findings in Abell S1063 (Sartoris et al. 2020). In particular, the X-ray hydrostatic analysis does not appear to underestimate the cluster mass.
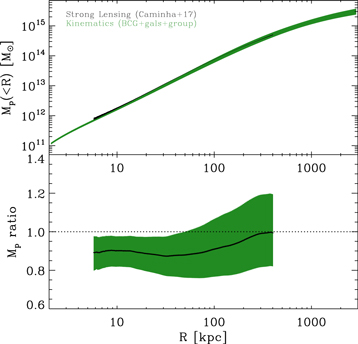
We compare the mass profile from Model 1 to the mass profile obtained by Caminha et al. (2017) based on a strong lensing analysis. We emphasize that the unusually large number of inner radial multiple images in M1206 (see Figure 2 of Caminha et al. 2017) translates into a very tight constraint of the (projected) inner density profile slope down to R ≃ 50 kpc. We show this comparison in Figure 8, where we display the projected mass profiles Mp ( < R), rather than the 3D ones, to ease the comparison with the strong lensing Mp (< R) of Caminha et al. (2017). To allow for a fair comparison between the kinematics and lensing estimates we must take into account the mass contribution by the foreground group already discussed in Section 2.1. This contribution is naturally included in the lensing estimate, but not in the estimate from kinematics, since the group galaxies are correctly excluded from our dynamical analysis since they are not cluster members.
Figure 8. Top panel: projected mass profiles Mp (< R) of the MACS 1206 cluster. Shadings indicate the 68% confidence regions on Mp (< R). Green shading: Mp (< R) obtained from the kinematics analysis described in this paper, with the contribution of a foreground group. Black shading: Mp (< R) obtained from the strong lensing analysis of Caminha et al. (2017). Bottom panel: ratio of kinematics to strong lensing Mp (< R). Shading indicates the 68% c.l.
Download figure:
Standard image High-resolution imageThis group of 15 galaxies is located close to the cluster center (<200 kpc) and has a line-of-sight velocity dispersion of 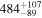 km s−1. Using the "AGN gal" relation of Table 1 in Munari et al. (2013), we estimate a group mass M200 ∼ 4–17 × 1013
M⊙. This group was already identified by Young et al. (2015) as residual Sunyaev–Zel'dovich emission left after subtracting a model emission by the main cluster. Young et al. (2015) also estimated the group mass by several methods. Our mass estimate is consistent with theirs (see Table 7 in Young et al. 2015).
km s−1. Using the "AGN gal" relation of Table 1 in Munari et al. (2013), we estimate a group mass M200 ∼ 4–17 × 1013
M⊙. This group was already identified by Young et al. (2015) as residual Sunyaev–Zel'dovich emission left after subtracting a model emission by the main cluster. Young et al. (2015) also estimated the group mass by several methods. Our mass estimate is consistent with theirs (see Table 7 in Young et al. 2015).
We do not have sufficient spectroscopic data to constrain the group mass concentration, so we use the mass-concentration relations of Dutton & Macciò (2014) and Correa et al. (2015b), to estimate c200 ∼ 5. By assuming that the group mass distribution follows an NFW profile, and by identifying the group center with the cluster center for simplicity, we can then estimate the group Mp (< R) and add it to the cluster Mp (< R) obtained from kinematics. We thus obtain the profile shown by the dark green shading in Figure 8, which is within the 68% c.l. of the strong lensing Mp (< R) for R > 50 kpc, and only slightly below at smaller radii. The remaining ∼10% disagreement may be due to our simplified assumptions on the mass profile of the foreground group and the position of its center, as well as on the spherical symmetry assumption used to project the cluster and group mass profiles.
5. Discussion
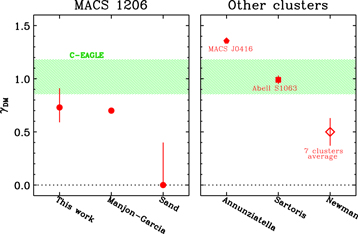
Our result for the inner slope of the DM density profile is 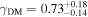 (68% c.l.), with an upper 95% c.l. of 1.04, consistent with the NFW slope (see Table 1). Previous results on the inner slope of the MACS 1206 mass density profile were obtained by Umetsu et al. (2012), Young et al. (2015), and Caminha et al. (2017) for the total mass and by S04 and Manjón-García et al. (2020) for the DM; we show the latter two results in Figure 9 together with our own. Umetsu et al. (2012) combined a weak-lensing distortion, magnification, and strong-lensing analysis, and found an inner slope value
(68% c.l.), with an upper 95% c.l. of 1.04, consistent with the NFW slope (see Table 1). Previous results on the inner slope of the MACS 1206 mass density profile were obtained by Umetsu et al. (2012), Young et al. (2015), and Caminha et al. (2017) for the total mass and by S04 and Manjón-García et al. (2020) for the DM; we show the latter two results in Figure 9 together with our own. Umetsu et al. (2012) combined a weak-lensing distortion, magnification, and strong-lensing analysis, and found an inner slope value 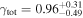 (68% c.l.). An almost identical, but more precise result, was obtained by the strong lensing analysis of Caminha et al. (2017), who found γtot = 0.91 ± 0.04 (68% c.l.). Young et al. (2015) modeled the Sunyaev–Zel'dovich emission by the cluster with a gNFW profile with γtot = 0.7 (no error bars provided). The results of Umetsu et al. (2012), Young et al. (2015), and Caminha et al. (2017) are not directly comparable to ours, as they did not constrain the DM profile inner slope.
(68% c.l.). An almost identical, but more precise result, was obtained by the strong lensing analysis of Caminha et al. (2017), who found γtot = 0.91 ± 0.04 (68% c.l.). Young et al. (2015) modeled the Sunyaev–Zel'dovich emission by the cluster with a gNFW profile with γtot = 0.7 (no error bars provided). The results of Umetsu et al. (2012), Young et al. (2015), and Caminha et al. (2017) are not directly comparable to ours, as they did not constrain the DM profile inner slope.
Figure 9. Summary of γDM measurements for clusters of galaxies. Error bars are 1σ. The green region indicates the standard deviation around the mean value for 16 massive halos in the C-EAGLE simulations analyzed by He et al. (2020). Left panel: results for MACS 1206. No error estimate is available for the value of Manjón-García et al. (2020). Right panel: results for other clusters, MACS J0416-2403 (pentagon, Annunziatella et al. 2017), Abell S1063 (square, Sartoris et al. 2020), and an average of seven cluster values (open diamond, Newman et al. 2013a). The error bar for the value of Annunziatella et al. (2017) is smaller than the symbol size, but not fully comparable to the other error bars in the figure because it is based on the simplified assumption of a power-law mass density profile.
Download figure:
Standard image High-resolution imageAccording to Schaller et al. (2015)'s analysis of the EAGLE cosmological simulations (Crain et al. 2015; Schaye et al. 2015), very massive halos/clusters (such as MACS 1206) have γtot − γDM ≈ 0.1, on average, a difference attributed to the stellar mass contribution of the BCG at the cluster center. If clusters have a similar baryon-to-total mass distribution as the numerical halos in the EAGLE simulations, we can conclude that the results of Umetsu et al. (2012) and Caminha et al. (2017) for γtot, are fully consistent with our result for γDM (we cannot make a statement about the result of Young et al. 2015 because we ignore its uncertainty). However, our result for the BCG M/L supports a bottom-heavy IMF, while the EAGLE simulations adopted a more conventional Chabrier (2003) initial mass function (IMF; Schaller et al. 2015) to convert the stellar masses to luminosities. The difference in the IMF implied by our dynamical analysis and the IMF adopted in the EAGLE simulations could be compensated by the fact that the simulated BCGs contain more stellar mass than observed BCGs by up to 0.6 dex (He et al. 2020). Given these uncertainties, it is not straightforward to estimate γDM from the observed γtot values.
Manjón-García et al. (2020) determined the MACS 1206 DM density profile via a strong lensing analysis, by subtracting the BCG stellar mass distribution. Unlike us, they did not account for the mass contributions of the satellites and the hot intracluster medium (ICM), but these are probably negligible in the inner cluster region. They found γDM = 0.7, which is in excellent agreement with our result, but they did not provide the uncertainty in their measurement.
S04 combined the dynamical analysis of the BCG stellar velocity dispersion with the constraints obtained by modeling the giant gravitational arcs, to determine the inner slope of the DM density profile. Also in this case, the satellites and ICM mass contributions were neglected. They found γDM = 0, with a 68% (respectively, 95%) upper limit γDM ≤ 0.40 (respectively, 0.67). Their result is therefore inconsistent with the NFW slope at the 95% c.l., and with our own result at the 68% c.l. A cored inner mass density profile was also found to be favored over a cuspy model by Limousin et al. (2022), even if these authors did not attempt to provide an estimate of γDM.
Part of the difference in S04's γDM value and ours may be related to the difference in the values of rρ
, since there is a strong covariance between rρ
and γDM, as shown in Figure 7 and as already pointed out by He et al. (2020) in a more general case. Our large spectroscopic data set for cluster galaxies allows us to directly constrain rρ
. On the other hand, S04 were unable to constrain rρ
from their lensing data and they had to fix it to an ad hoc value, rρ
= 0.4 Mpc. Their adopted value agrees with the estimate of (Umetsu et al. 2012, 0.28 ± 0.06 Mpc for a gNFW model) based on gravitational lensing, but not with the estimate of (Donahue et al. 2014, 0.64 ± 0.15 Mpc) based on X-ray Chandra data. Our independent analysis of X-ray data confirms the value of Donahue et al. (2014); we find  Mpc in excellent agreement with the value we obtain from our kinematical analysis
18
(see Table 1). Maybe the smaller rρ
value obtained by the lensing analyses compared to the X-ray and kinematics analyses, is due to the projected group near the center that we discussed at the end of Section 4. In any case, even if we force rρ
to the value adopted by S04 we would find γDM ≈ 0.6, still significantly greater than zero (see Figure 7).
Mpc in excellent agreement with the value we obtain from our kinematical analysis
18
(see Table 1). Maybe the smaller rρ
value obtained by the lensing analyses compared to the X-ray and kinematics analyses, is due to the projected group near the center that we discussed at the end of Section 4. In any case, even if we force rρ
to the value adopted by S04 we would find γDM ≈ 0.6, still significantly greater than zero (see Figure 7).
We think that the main reason for the difference between our and S04's γDM values is in the BCG data. While the BCG apparent magnitude estimate of S04 is similar to ours (in a slightly different band), they estimate Re = 12 kpc (converting their published value to our adopted cosmology), a factor ∼2 smaller than our estimate. Moreover, their BCG velocity dispersion values, obtained with single slit observations with ESI@Keck II, are significantly smaller than our measurements, obtained with MUSE@VLT integral field observations (compare Figure 7 and Table 5 in S04, with Figure 4). S04's BCG velocity dispersion values are 54 and, respectively, 119 km s−1 below our values in the radial ranges where they made their estimates, 0–6 and 6–28 kpc, respectively, corresponding to an 18% and 32% underestimate, respectively. The superior quality of our MUSE measurements appears therefore crucial in achieving an accurate γDM determination.
Our γDM value for MACS 1206 is somewhat below the NFW profile value, while we found almost exactly the NFW value for the cluster Abell S1063 that we analyzed with the same methodology in Sartoris et al. (2020, γDM = 0.99 ± 0.04). Part of the difference among these values could be related to the general assumption of spherical symmetry combined with different levels of triaxiality and different orientations with respect to the line of sight. However, the study of Sereno et al. (2018) finds very similar triaxial shapes and orientations for the two clusters, so the difference in their γDM values is probably intrinsic.
According to Sereno et al. (2018), the orientation of the major axis of MACS 1206 with respect to the line of sight is 78°, and this is also suggested by the very elliptical projected shape of the BCG. The study of He et al. (2020), based on the C-EAGLE numerical simulations, shows that the value of γDM inferred under the spherical symmetry assumption can differ from the intrinsic value by ±0.2 rms, with a negative bias of −0.2 when the BCG is viewed along its minor axis (see Figure 15 in He et al. 2020). The intrinsic value of γDM of MACS 1206 could then be even closer to the NFW value than we find in our analysis. In any case, our γDM value for MACS 1206 is in agreement with the expectations for massive halos from the C-EAGLE simulations of He et al. (2020), which suggests a decreasing trend of γDM with halo mass (halos as massive as MACS 1206 have γDM ≈ 0.8 rather than 1, see He et al. 2020).
Unlike the high γDM values of Abell S1063 and MACS J0416-2403, our result is not in contrast with the observational results of Newman et al. (2013a), who found an average value of γDM = 0.50 ± 0.13 over seven clusters (we show these γDM values in Figure 9). However, Newman et al. (2013a)'s value is in significant tension with pure-CDM halo inner slope values, while our value for MACS 1206 is not.
The intermediate γDM value we find for MACS 1206 therefore removes the tension with CDM models that was created by the previous measurement of S04, and suggested by the analysis of Limousin et al. (2022), but it does not allow for the rejection of alternative DM models to CDM, such as the self-interacting DM model of Spergel & Steinhardt (2000). The difference with the γDM value of the Abell S1063 cluster that we analyzed with the same technique and data of the same quality suggests that different physical processes have been or are now at work in the central regions of these two clusters, shaping the inner slope of the DM profile, or that we observe the two clusters at different stages of their evolution. Clearly, precise γDM determinations for more clusters are needed to investigate this topic.
6. Summary and Conclusions
We determined the total mass profile of the z = 0.44 massive cluster MACS 1206, from 2 kpc to 2 Mpc, and separately, its DM and baryonic components. This result was obtained by applying an extension of the MAMPOSSt method (Mamon et al. 2013; Pizzuti et al. 2023) to maximize the combined likelihoods of the observed BCG velocity dispersion profile and the velocity distribution of cluster member galaxies. Our total mass profile is in remarkable agreement with independent determinations based on X-ray observations and strong lensing (Caminha et al. 2017), after accounting for the mass contribution of a foreground group of galaxies to the strong lensing signal. This comparison also shows no significant evidence of a hydrostatic bias, often claimed in X-ray cluster mass profile determinations.
As an additional output of our analysis, we constrained the BCG stellar velocity anisotropy to be close to isotropic, as expected based on previous works on giant ellipticals (Kronawitter et al. 2000; Santucci et al. 2023). We found that the orbits of cluster galaxies are radially elongated, increasingly with radius, a feature common to most clusters (e.g., Natarajan & Kneib 1996; Biviano et al. 2013; Mamon et al. 2019; Biviano et al. 2021).
Our main result is the determination of the DM profile inner slope,  (68% c.l.) ±0.3 (95% c.l.), the most accurate determination for this cluster so far. Our value is somewhat below the NFW profile slope predicted in CDM simulations, but fully consistent with it when considering the scatter in the inner slopes of DM halos and the decreasing trend of γDM with halo mass (He et al. 2020). Our value does not support the claim of a cored inner mass distribution for this cluster by Limousin et al. (2022), and it is significantly larger than the γDM measurement by S04 for the same cluster, a difference that we attribute to the significantly increased accuracy and precision of our BCG velocity dispersion profiles measurement.
(68% c.l.) ±0.3 (95% c.l.), the most accurate determination for this cluster so far. Our value is somewhat below the NFW profile slope predicted in CDM simulations, but fully consistent with it when considering the scatter in the inner slopes of DM halos and the decreasing trend of γDM with halo mass (He et al. 2020). Our value does not support the claim of a cored inner mass distribution for this cluster by Limousin et al. (2022), and it is significantly larger than the γDM measurement by S04 for the same cluster, a difference that we attribute to the significantly increased accuracy and precision of our BCG velocity dispersion profiles measurement.
Our results for the massive clusters MACS 1206 and Abell S1063 (previously analyzed with the same methodology by Sartoris et al. 2020) appear in very good agreement with state-of-the-art Lambda CDM numerical simulations, at variance with the findings of S04 and Newman et al. (2013a). More high-quality measurements of γDM are needed to determine its distribution across different clusters, and, in combination with cluster properties, understand the physical origin of its scatter.
Acknowledgments
We dedicate this work to the memory of our beloved friend and esteemed colleague Mario Nonino. We thank Carlos Frenk for the useful discussion. We thank the anonymous referee for her/his report that helped improve this paper. We acknowledge financial support through grants PRIN-MIUR 2017WSCC32. A.B. acknowledges the financial contribution from the INAF mini-grant 1.05.12.04.01 "The dynamics of clusters of galaxies from the projected phase-space distribution of cluster galaxies." L.P. acknowledges support from the Czech Academy of Sciences under grant No. LQ100102101. S.E. acknowledges the financial contribution from the contracts ASI-INAF Athena 2019-27-HH.0, "Attività di Studio per la comunità scientifica di Astrofisica delle Alte Energie e Fisica Astroparticellare" (Accordo Attuativo ASI-INAF n. 2017-14-H.0), and from the European Union's Horizon 2020 Program under the AHEAD2020 project (grant agreement No. 871158).
Footnotes
- 15
Based on the GTO programs 095.A-0181(A), 097.A-0269(A) (P.I. J. Richard).
- 16
Here and throughout this paper, we call rΔ the radius that encloses an average density Δ times the critical density at the halo redshift. MΔ is related to rΔ by
 /G, where Hz
is the Hubble constant at the cluster redshift and G is the gravitational constant.
/G, where Hz
is the Hubble constant at the cluster redshift and G is the gravitational constant. - 17
The new method is described in Pizzuti et al. (2023) and freely available at https://github.com/Pizzuti92/MG-MAMPOSSt and on Zenodo (Pizzuti et al.2023).
- 18