Abstract
We propose a novel synaptic design of more efficient neuromorphic edge-computing with substantially improved linearity and extremely low variability. Specifically, a parallel arrangement of ferroelectric tunnel junctions (FTJ) with an incremental pulsing scheme provides a great improvement in linearity for synaptic weight updating by averaging weight update rates of multiple devices. To enable such design with FTJ building blocks, we have demonstrated the lowest reported variability: σ/μ = 0.036 for cycle to cycle and σ/μ = 0.032 for device among six dies across an 8 inch wafer. With such devices, we further show improved synaptic performance and pattern recognition accuracy through experiments combined with simulations.
1. Introduction
The neuromorphic hardware with memristive synapses enables energy-efficient data processing for artificial intelligence (AI) and machine learning, where most of the computing workload is vector-matrix-multiplications (VMMs) in neural networks [1–6]. The learned weights of the neural networks are stored in the nonvolatile memristive synapses, and computing during inference is essentially just applying small voltages to the synapses and reading the output currents. Multiply and accumulate (MAC) operations among the neuronal layers are executed directly by Ohm's law and Kirchhoff's current law, respectively. These operations take place where the data, i.e. weights of the neural network models, are stored and thus obviate the time- and energy-consuming data movements that limit the performance of the traditional von Neumann computing architecture. In addition, all the MAC operations happen in parallel across the entire neural network. Moreover, the system can deal with analogue input data (e.g. data from analogue sensors) directly without the need of digitizing the data first. Therefore, such hardware accelerating systems enabled by memristive synapse are capable of in-memory, parallel and analogue computing, leading to orders of magnitude improvements in energy efficiency and throughput in performing VMMs over the traditional digital systems. As the critical enabler of the accelerators, memristive synapses need to meet certain performance requirements for both inference and learning. For inference, the main requirements are similar to those for nonvolatile memories, such as retention, multilevel states, and 3D stackability. In addition, different from memory applications, all the cells in the entire neural network are operated simultaneously and therefore a relatively high resistance for each cell is important to avoid too high current and energy in the neural networks. For in-situ learning within the memristive neural network, it is highly desirable to have a linear and symmetric programming capability in the cell for efficient learning.
Two-terminal memristive devices have been highly desirable due to their area-efficiency and convenience in directly utilizing physics laws for computing. However, most of resistive switching memories have been suffered from the reliability issue, especially variability. Despite a neural network is adaptive during in-situ training and thus error-tolerable to a certain degree, variability of synapses such as cycle-to-cycle (C2C) and device-to-device (D2D) variations have resulted in degraded performance in both training and inference accuracy [7]. Such variabilities of the resistive switching phenomena in memristive oxides originates from their localized ion migrations with intrinsic stochasticity and randomness. Without random ion migrations involved in the switching mechanisms, ferroelectric (FE) polarization based switching is expected to be more immune from such variabilities. In addition, tunneling based electron transport mechanisms in such devices endow them with a higher resistance regime than the filamentary memristive devices. Accordingly, among all the nonvolatile memories studied as memristive synapses, such as resistive switching memories, spintronic memories, phase change memories and devices based on FE materials [8–21], ferroelectric tunnel junction (FTJ) is an attractive candidate due to its non-filamentary nature, high-endurance and relatively high resistance and low current [22–25].
Unfortunately, FTJs exhibit a nonlinear and asymmetric weight updating behavior under identical pulses due to their intrinsic physics. Polarization switching kinetics of FE is proportional to −exp{−(t/t0)n }, where t0 is a characteristic switching time which is a function of the applied field, t is switching time and n is the geometric dimensionality for domain growth. Hence a synapse with a single FE device, of which the synaptic weight is proportional to polarization state, usually exhibits a nonlinear weight update driven by identical pulses. Even worse, intrinsic nonlinear switching characteristics of FE due to an abrupt switching at the coercive voltage (Vc) have resulted in a much-degraded linearity. Accordingly, incremental step pulses (ISPs) have been commonly employed to mitigate the nonlinear weight update issue, but only to a certain degree [12, 20]. Recently, two transistor—one ferroelectric field effect transistor (FeFET) synapse solution was proposed to implement least significant bits (LSBs) and most significant bits (MSBs) for training and inference, respectively [16]. A symmetric and linear weight update of LSBs during the training with identical pulses demonstrated a high accuracy approaching that obtained by software simulations. However, non-volatile MSBs still updated by ISPs. More importantly, such synapses occupied a large area of chip due to three transistors used for each synapse. Another approach to improve linearity was developed by modulating the microscopic structure of FE layer. Considering the multi-level characteristics originated from the multi-domain nature of FE, Akif Aabrar et al increased the number of domains by interposing a dielectric layer between FE layers [17]. As a result, Vc was distributed along voltage so that synaptic weight was linearly updated according to ISPs, while applied voltage dropped across the extra interposed dielectric layer resulting an undesirable increase of the programming voltage.
In this work, a novel artificial synapse based on multiple FTJs was designed to improve the linearity of weight update and minimize the variability. The variability issue has been mitigated by the low variability of our individual FTJs of which the mean to deviation ratios (σ/μ) of C2C and D2D are 0.036 and 0.032, respectively. As shown in figure 1, individual FTJs are connected in parallel to construct a synaptic device. Thanks to the 3D integration of the HfO2-based FE devices on CMOS [25–27], a conceptual synapse with vertically stacked FTJs (figure S1) in the future will be able to avoid an increase in footprint. Due to different voltage offsets at the lower end of each FTJ as shown in figure 1(b), a voltage pulse from the upper end of the FTJ set (from the access transistor in the schematic) will result in different voltage drop on each of the FTJs of the device set. Therefore, each FTJ will follow different segments of the switching curve (i.e. experiencing different stages of switching) driven by applied ISPs on the upper end of the FTJ set, as schematically shown in figure 1(a). Although each of the segment is still nonlinear with the ISP pulse number, the combination (linear summation as they are connected in parallel) of them will be much more linear, leading to a greatly improved linearity in programming for training. The nonlinearity (α) of such synapse can be calculated based on the measured nonlinear switching curve for a single FTJ, which shows that the nonlinearity has been improved from −3.25/−2.51 (for a single-FTJ synapse) to −0.18/−1.14 (for a synapse based on four parallel FTJs) in potentiation and depression operations, respectively. Such nonlinearity enables 96.84% pattern recognition accuracy obtained from neural network simulations with MNIST dataset, which is close to the software limit (97.26%)
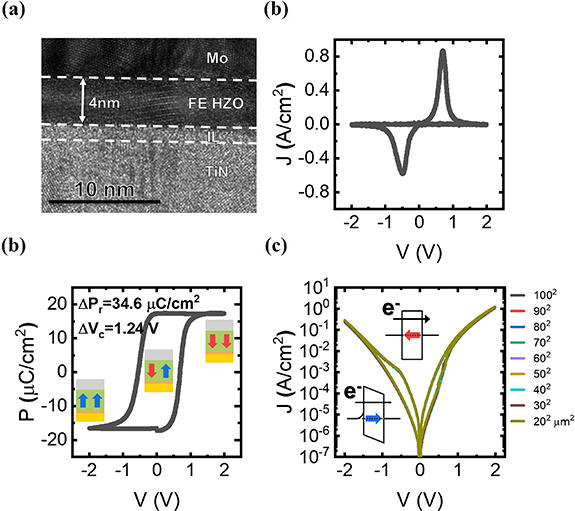
Figure 1. (a) The synaptic weight (polarization or conductance) of the ferroelectric memristors abruptly changes when the pulse amplitude overcomes the nominal coercive voltage. Nonlinearity in weight update of each memristors programmed by different pulse amplitude ranges can be ruled out by parallel summation of the read current (b), (c) Circuit diagrams with respective node voltages for program (training) and read (inference), respectively.
Download figure:
Standard image High-resolution image2. Fabrication and method
FTJ was fabricated as following sequences. A highly doped p-type 8 inch silicon wafer was dipped into diluted hydrofluoric acid solution. A 50 nm-thick TiN bottom electrode was sputtered on cleaned substrate and then its surface was oxidized through ozone pretreatment to form an interfacial layer (IL). A 4 nm-thick (Hf,Zr)O2 film was deposited by thermal atomic layer deposition (ALD) at 300 °C with TEMA-Hf, TEMA-Zr and ozone. Following the sputtering of 50 nm-thick Mo top electrode, N2-ambient rapid thermal annealing at 500 °C for 1 min was applied to crystalize the thin film into non-centrosymmetric FE phase. The top electrodes, of which size was varied from 400 to 10 000 μm2, were patterned by dry etching.
All of the electrical measurements were carried out on 8 inch semi-auto probe station with Keithley SCS4200 equipped with pulse-measure-units and source-measure-units. A pulse train of positive-up-negative-down (PUND) was used to measure FE hysteresis curves. DC current–voltage measurements were performed to confirm the conductance change and reliability of the devices. A customized pulse-write and DC-read measurement protocol was used to characterize the long-term potentiation and depression (LTPD) of synapse.
3. Results and discussion
According to the nucleation limited switching model [28, 29], polycrystalline FE thin films are switched in domain-by-domain manner where Vc of the domains are dispersed. The majority of the domains are flipped at the nominal Vc of which the maximal switching current flows when the FE hysteresis is measured as shown in the upper-left panel in figure 1(a). Some portions of the domains, however, are flipped at voltages greater than or less than the nominal Vc, leading to Gaussian distribution-like curves of displacement current versus voltage. As the conductance of FTJ is strongly dependent on the polarization of FE layer, which is closely related to domain configurations [22], the conductance corresponding to the programming voltage is also abruptly changed around the nominal Vc. This is undesirable for training applications. Therefore, a feasible solution for implementing FTJs into synapses is needed to make FE switching uniform corresponding to the programming voltage. In our proposed synaptic design, multiple parallel FTJs connecting to the drain of the access transistor in a vertical fashion while the plate lines (PLs) of individual FTJs are shared with the FTJs of a neighboring synapse as shown in figure S1. The vertical structure ensures identical footprint of the synapse even when the number of parallel FTJs increases. Operation schemes with circuit diagrams for program (training) and read (inference) are illustrated in figures 1(b) and (c), respectively. For the case of program, the word line is firstly biased to turn-on the access transistor, and then a programming pulse is applied to the source line while each of the PLs is biased to a constant voltage with an identical amplitude gap among these constant voltages. For the case of read, read voltage (or input for inference) is applied to the source line while all the PLs are grounded so that current through FTJs are accumulated, thus the total conductance (synaptic weight) is determined from total current flowing through the synapse consisting of the parallel set of FTJs. Being applied with a bias voltage of different amplitude, the synaptic weight (conductance or polarization) in each FTJ is modulated in different stages with respect to the nominal Vc of FE film at early (green), mid (red and blue), and late (black) stages as shown in the middle panel in figure 1(a). The black dots in the lower-left panel in figure 1(a) are the trail of the polarization (or conductance, i.e. corresponds to the synaptic weight) along the full sweeping range. The voltage (pulse amplitude, lateral axis in the upper- and lower-left panels) corresponds to the pulse number of the ISPs for programming. The voltage gaps between respective ranges of ISP (pulse amplitude range) are identical, i.e. ΔV. Consequently, the conductance change of unified parallel FTJs (purple) along with the pulse number (LTPD characteristics) exhibited a much-improved linearity, in contrast to the nonlinearity (black, red, blue, and green) induced by abrupt changes in the right panel in figure 1(a).
While experimentally building the 3D structure schematically shown in figure S1 will be a major achievement to be demonstrated in the future, the switching reproducibility of individual FTJs and their uniformity across a large wafer are critical for enabling our novel synaptic design and need to be demonstrated first. The individual FTJs, as the building blocks of the synapses, were fabricated with a TiN bottom electrode, a Mo top electrode and a HfO2-based FE layer. An ozone oxidation before FE film deposition formed about 1 nm-thick IL between the TiN bottom electrode and FE layer as shown in figure 2(a). The IL induced more asymmetry of the potential across the FTJ stack, increasing the tunneling electroresistance (TER). Before performing the FE measurement, 1000 cycles of 2 V amplitude wake-up pulses with a frequency of 100 kHz were applied to achieve a full switching of the FE layer. Due to the thin thickness of the FE layer, a large current flew through the FTJ and the conventional triangular pulse measurement is improper to investigating the FE properties. Accordingly, a PUND measurement with 10 kHz pulses was carried out. Sharp FE switching current peaks were observed at around +0.8 V and −0.5 V as shown in figure 2(b), revealing a good uniformity across the device area. The displacement current was integrated over time to obtain a polarization–voltage (PV) curve. In figure 2(c), the switchable polarization, 2Pr, was about 35 μC cm−2, indicating a good FE property. The memory characteristics of the FTJ was investigated through DC current–voltage (IV) measurement with different device areas ranging 400–10 000 μm2. The current density curves of different-sized devices were nearly perfectly overlapped as shown in figure 2(d). Such area-independent current density is challenging to achieve, if possible, at all, in filamentary-type resistive switching memory or phase change memory. This has a great advantage in neural network design where the current through the network can easily become enormous due to an extremely large number of the devices in the network [30, 31]. The fact that the current can be reduced by dimension scaling in FTJs is highly attractive as it alleviates the concerns of high energy consumption and current saturation in the peripheral circuitry when the neural network size is scaled up and the technology node is scaled down. Although relatively low conductance benefits the network with a smaller voltage drop on the parasitic resistance in the transmission line, too low conductance of the FTJ incurs expensive analogue-digital conversion and reduces the speed of operation. Further research on barrier engineering, thickness scaling or electrode workfunction optimization, may improve the conductance of the FTJ to an appropriate level, which has not been addressed in this study. The conductance of FTJ displayed hysteresis along the voltage sweep direction. TER at 0.2 V was about 10 and it does not significantly change in the middle of the hysteresis. The voltage range of observed hysteresis in DC IV characteristics was consistent with that of the PV hysteresis. Note that there is no current deviation between forward and backward sweep in the IV curve beyond the completion of FE switching, indicating that additional resistance change due to oxygen vacancy migration can be largely excluded [24]. The device endurance and data retention are also crucial for synapse applications, since the synapse frequently switches its memory state during the training or programming and maintain the programmed state during inference or read operations. Figure S2 showed superior endurance and retention characteristics of the FTJ. The endurance of the conductance switching was monitored by a DC IV measurement after applying square pulses with an amplitude of 2 V at a frequency of 500 kHz. To minimize the time constant (RC delay) of the device under test, 400 μm2-sized device was utilized, ensuring the full switching of the FE layer. The FTJ endured up to 108 cycles without breakdown and largely maintained its TER. The data retention was tested after applying DC bias by measuring the current at the read voltage of 0.2 V. The low and high resistance state (LRS and HRS) were programmed by +2 and −2 V, respectively. In addition, the intermediate resistance state was investigated by applying +0.8 V on HRS. At room temperature, three data states were maintained for 30 000 s and the estimated data retention period was more than ten years, while the retention loss might be accelerated at elevated temperature. The resistance of LRS increased over time while that of HRS slightly decreased. Consequently, the resistance of IRS slightly increased which is a moderate change compared to LRS and HRS. The data retention loss rate of other IRSs would be smaller than LRS or HRS considering that IRS in FTJ results from horizontal configuration of LRS and HRS domains (see IRS in figure S2(b)). For instance, IRS with a lower resistance would lose its data retention faster than IRS with a higher resistance, since the fraction of LRS domain in IRS with a lower resistance is higher. A small narrowing of the memory window was observed, but it was acceptable because of the significantly lower dispersion of the memory states to be discussed later.
Figure 2. (a) Cross-sectional TEM image of the FTJ showing well-crystallized FE layer with flat and clean interfaces. (b) Transient current density vs. voltage and (c) polarization vs. voltage from PUND measurement. (d) DC current vs. voltage curves for various device sizes, showing robust ferroelectricity of the FE film (ΔPr = 35 μC cm−2). Insets in (c) and (d) depict domain configuration and tunnel band structures, respectively, with respect to polarization direction.
Download figure:
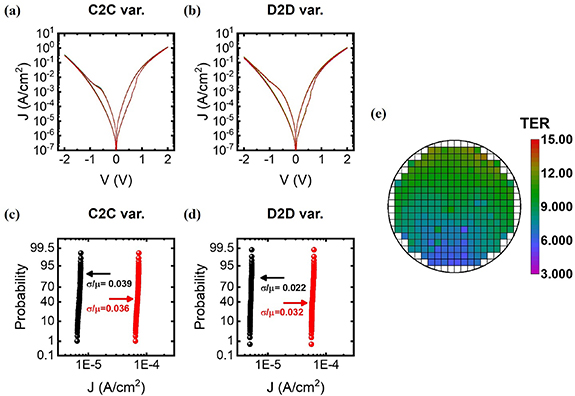
Standard image High-resolution imageSince the conductance switching of the FTJ solely depends on the FE polarization, which is domain configuration, it has led to an extremely low variability as shown in figure 3. The C2C variability of 100 cycles in a single device and the D2D variability of 100 devices in the nearest six dies were evaluated with DC IV measurements as shown in figures 3(a) and (b), respectively. The IV curves in both graphs were well matched, suggesting an extremely low variability of the FTJs. It is worth noting that the IV curves in figure 3(a) shifted upward as repeating the DC cycle. The current through the FTJ might increase due to a continuous wake-up caused by DC stress [32, 33], despite that a wake-up cycling had been performed, or due to trap formation in a thin film which results in stress induced leakage current [34, 35]. The cumulative probability of the on and off current at 0.2 V was plotted, to analyze the variability in a more quantitative way as shown in figures 3(c) and (d). For the case of the C2C variability, the relative standard deviation, namely, the ratio of the standard deviation to the mean, of the HRS and LRS were 0.039 and 0.036, respectively, while those of the D2D variability were 0.022 and 0.032, respectively. One thing should be noted that the C2C variability mostly comes from the current drift as mentioned above rather than the randomness. Such a low variability could ensure the reliability of operation of a single synaptic device and a large array of them. TER at 0.2 V of selected device in each die was spatially mapped across the 8 inch wafer, as shown in figure 3(e). One device per die could represent each die, since the D2D variability in a die was negligible as previously discussed. Although TER in most of wafer was about 10, a small TER gradient arose in the vertical direction. The degradation of TER uniformity was originated from the non-uniform FE layer thickness due to travelling-wave typed ALD chamber, which led to film thickness gradient along gas injector to pumping line. It is believed that more advanced manufacturing technology will effectively improve the uniformity and the D2D variability.
Figure 3. (a), (b) Overlaid DC IV curves and (c), (d) cumulative probability of HRS and LRS for 100 cycles from the same device and 1 cycle from 100 devices along 6 dies across an 8 inch wafer, respectively. Current density values were acquired at read voltage of 0.2 V (e) wafer mapping of TER from 8 inch wafer.
Download figure:
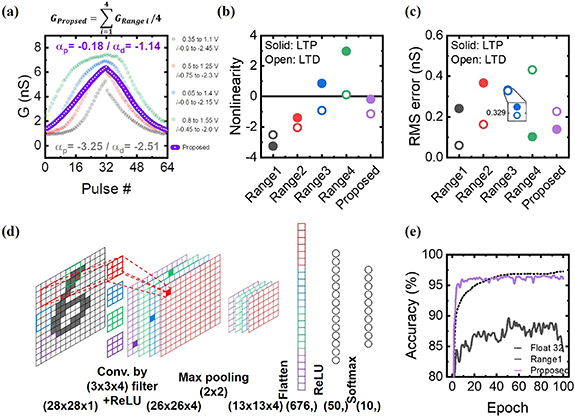
Standard image High-resolution imageAs a proof of concept, feasibility of the FTJ on synapse unit was examined with respect to the basic synapse function, LTPD, for neuromorphic MAC accelerator. Firstly, LTPD characteristics of a single FTJ was investigated with four respective pulse amplitude ranges. As shown in figure S3, the pulse sets of potentiation and depression were 32 incremental steps of which pulse amplitude varies with the minimum and the maximum being 0.75 V and −1.55 V, respectively, while pulse width was kept constant at 500 ns. The conductance was evaluated by DC read voltage at 0.2 V after applying each potentiation or depression pulse. The Vc became greater than what was shown in figure 2(b) since the Vc of FE film is strongly dependent on measure frequency [36, 37]. Pale black dots in figure 4(a) are LTPD of the FTJ when initial pulse amplitudes of potentiation and depression were 0.35 and −0.9 V, respectively. At the beginning of potentiation, 0.35 V was much lower than the nominal Vc, resulting in a tiny increase of the conductance because the FTJ rarely switched at the pulse less than Vc. As the pulse amplitude reached to the sub-Vc range, the slope of LTPD increased which indicates more domains were flipped per each pulse, resulting in a convex curve. However, −0.9 V was comparable to the negative Vc. Therefore, the conductance rapidly reduced at the initial stage of depression. As the pulse amplitude was negatively increased, most of domains had already been reversed and the conductance change slowed down, resulting in a convex curve too. In contrast, pale green dots in figure 4(a) (initial pulse amplitude were 0.8 and −0.45 V for potentiation and depression, respectively) exhibited concave potentiation and depression curves, opposite to the black dots. On the other hand, pale red and blue dots in figure 4(a) showed an inflected curve, from convex to concave, in both potentiation and depression. This is general response of FE devices when wide range of incremental pulses, with the nominal Vc in the middle, are applied [12, 16, 18, 23]. A negligible conductance switching occurred at lower and higher pulse amplitudes than Vc because the domains were not switched by a voltage lower than Vc and the domains had been already switched at a higher pulse. The conductance changed rapidly when the applied pulse amplitude was near Vc since most of the domains were reversed at around Vc. The initial pulse amplitude for potentiation and depression were {0.35, −0.9}, {0.5, −0.75}, {0.65, −0.6} and {0.8, −0.45} V, respectively. Those were identical situations with applying the same pulses on the top electrode while biasing the bottom electrode to 0, −0.15, −0.3 and −0.45 V, respectively, which is just congruent with programming scheme in figure 1(b). Therefore, the sum of the four LTPD curves (linearly, averaged to scale) resulted in the characteristics of the conceptual device proposed in figure 1. The purple curve in figure 4(a) is the LTPD characteristics of the proposed synapse device with four parallel FTJs, which exhibits a significantly improved linearity. However, the dynamic range, i.e. the maximum to minimum conductance ratio, was degraded to 5, which is a half of the TER, averaging out nonlinearity. A memristive neural network was simulated with the device parameters which are extracted from exponential curve fitting of the LTPD as equation (1) [38],
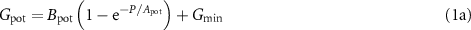
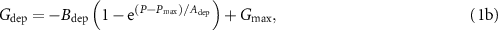
Figure 4. (a) LTPD characteristics, (b) nonlinearity labels, and (c) root-mean-square errors of single FTJ with various pulse amplitude ranges (black, red, blue, and green) and those of the proposed design (purple), i.e. an average of the other four curves. The proposed design does not only exhibit improved linearity, but also fits to exponential model well. (d) Schematic diagram of simulated convolutional neural network for the MNIST test. (e) The recognition accuracy of the floating point-based software and the device parameter from the range 1 (black in (a)) and the proposed design (purple).
Download figure:
Standard image High-resolution imagewhere P is the pulse number, B is a coefficient which is a function of A, A is an exponent that determines the nonlinear shape of the curve, Pmax is the maximum pulse number, Gmin is the minimum conductance, and Gmax is the maximum conductance. The five LTPD curves are fitted with exponential function as shown in figure S4. The nonlinearity label, α, is converted from A and plotted according to the programming condition as shown in figure 4(b). Figure 4(c) displays root-mean-square (RMS) errors to evaluate how accurately it models the measured data. The proposed device exhibited much lower nonlinearity than those of individual FTJs with the various pulse amplitude ranges in both the potentiation and the depression. The range 2 and range 3 also showed a relatively low nonlinearity. However, the RMS errors were large due to an inflected curve shape indicating that the curves were not precisely modeled. The proposed synaptic design simultaneously provided low nonlinearity and precise modelling capability. Classification test was carried out with MNIST dataset to evaluate the efficiency of analogue MAC accelerator for online training. The neural network was simulated based on the device parameters of the proposed artificial synapse rather than implementing a real array. The neural network consisted of one convolution layer with four (3 × 3) filters, one (2 × 2) max pooling layer and a fully-connected layer with one hidden layer (676 × 50 × 10, ReLU and softmax activation for respective layers), as shown in figure 4(d). The accuracy from floating point-based software reached as high as 97.26% (dotted line in figure 4(e)). For memristive neural network training, the weight update was calculated with backpropagated errors and the weights are potentiated or depressed based on the sign of calculated weight update, namely, Manhattan update rule [39]. The memristive neural network based on the single FTJ with the range 1 (pale black in figure 4(a)) showed much degraded accuracy of 89.48% due to the non-ideal behavior of the device, namely, nonlinear and asymmetric weight updates. On the other hand, a high accuracy of 96.84% was achieved by the proposed device, which is close to that obtained with software. The simulation result of the other FTJs with different pulse amplitude ranges are plotted in figure S4(f). The simulation result by using experimental data directly is also plotted in figure S4(g). The energy efficiency of memristive synapse is key feature for implementing memristive neuromorphic chips. The average energy consumption of the FTJ per programming pulse was 130.1 fJ μm−2 and the maximum power consumption during the read operation was 146 fW μm−2. The details for energy consumption can be found in supplementary information.
The performance of the proposed synaptic device is compared with previous reports, as shown in table 1. Although the dynamic range and the number of conductance levels are relatively low for the synapse of this study, other properties, including nonlinearity, asymmetry, and variation, are superior to previously reported two-terminal devices. The operation voltage of three-terminal analogue devices based on FeFET were relatively high. The FeFET usually needs higher voltages to switch the FE layer than FTJs because the voltage applied on the gate is divided onto the FE layer and channel or other dielectric layers. Unfortunately thinning the FE layer in the gate is unfavored due to the increase of the leakage current, which limits the operation voltage scaling. Therefore, our artificial synapse with FTJs would be a promising solution for energy-efficient, low-voltage and accurate analogue MAC accelerators.
Table 1. Benchmark of device characteristics with other reports.
| Devices | AlOx /HfOx RRAM | Ag:a-Si CBRAM | HfOx /AlOy Superlattice | Te/MgO/HfOx CBRAM | IGZO FeFET | 2T-1FeFET | Superlattice FeFET | 1T-1R 28 nm FDSOI | Parallel FTJ |
|---|---|---|---|---|---|---|---|---|---|
| Nonlinearity | 1.94/−0.61 | 2.4/−4.88 | 1.44/2.55 | 1.36/2.18 | −0.8/−0.69 | 0.5/0.5 | −0.7/−1.56 | N/A | −0.18/−1.14 |
| Asymmetry | 2.55 | 7.28 | 1.11 | 0.82 | 0.11 | 0 | 0.86 | N/A | 0.96 |
| Voperating (V) | 0.9/−1 | 3.2/−2.8 | 1.4/−1.6 | 0.7/−0.73 | 4.3/−3.6 | 4/−4 | 4.77/−1.77 | 2.7 | 1.55/−2.45 |
| # of G states | 40 | 97 | 100 | 500 | 64 | 64 | 128 | 2 | 32 |
| Gmax/Gmin | 4.43 | 12.5 | 5.5 | 1.13 | 14.4 | 45 | 285.7 | 3 | 5 |
| C2C variation | 3.5% | 5% | N/A | N/A | 2.36% | N/A | N/A | N/A | <1% |
| Accuracy | 20% | 72% | 94.95% | N/A | 91.1% | 94.3% | 94.1% | N/A | 96.84% |
| References | [8] | [9] | [10] | [11] | [15] | [16] | [17] | [40] | This work |
4. Conclusion
A novel synaptic design with FTJs is proposed and the concept is applicable to other FE memories as well. This general-purpose design may substantially enhance the performance of edge AI computing with FE devices. In the new design, the abrupt change of the conductance near Vc has been mitigated by averaging out the switching rate through employing different pulse amplitude ranges on multiple devices. FTJs with extremely low variabilities in both C2C and D2D have been demonstrated at wafer level, which also exhibit reliable memory operations and low operation voltages. Four of such FTJ devices with parallel arrangement and respective incremental pulses on them have been shown to greatly reduce the intrinsic non-linearity of FE based synaptic devices. Such design can conveniently leverage the trend of 3D integration scheme with a footprint of 5F2, which will accelerate the realization of on-device neuromorphic hardware.
Acknowledgments
This work was partially supported by the Air Force Office of Scientific Research (AFOSR) for support through the MURI program under Contract No. FA9550-19-1-0213 and the USA Air Force Research Laboratory (AFRL) (Prime Contract Nos. FA8650-21-C-5405 and FA8750-22-1-0501).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Supplementary data (0.4 MB PDF)