Abstract
Solar flare prediction plays an important role in understanding and forecasting space weather. The main goal of the Helioseismic and Magnetic Imager (HMI), one of the instruments on NASA's Solar Dynamics Observatory, is to study the origin of solar variability and characterize the Sun's magnetic activity. HMI provides continuous full-disk observations of the solar vector magnetic field with high cadence data that lead to reliable predictive capability; yet, solar flare prediction effort utilizing these data is still limited. In this paper, we present a machine-learning-as-a-service (MLaaS) framework, called DeepSun, for predicting solar flares on the web based on HMI's data products. Specifically, we construct training data by utilizing the physical parameters provided by the Space-weather HMI Active Region Patch (SHARP) and categorize solar flares into four classes, namely B, C, M and X, according to the X-ray flare catalogs available at the National Centers for Environmental Information (NCEI). Thus, the solar flare prediction problem at hand is essentially a multi-class (i.e., four-class) classification problem. The DeepSun system employs several machine learning algorithms to tackle this multi-class prediction problem and provides an application programming interface (API) for remote programming users. To our knowledge, DeepSun is the first MLaaS tool capable of predicting solar flares through the internet.
1. Introduction
Solar flares and the often-associated coronal mass ejections (CMEs) highly impact the near-Earth space environment (Liu et al. 2017; Liu et al. 2020a). They have the potential to cause catastrophic damage to technology infrastructure (Daglis et al. 2004). According to the U.S. National Space Weather Strategy, released by the Space Weather Prediction Center, it is a challenging task to correctly predict solar flares and CMEs. Recent efforts led by the United States and its partners resulted in substantial progress toward monitoring, prediction and mitigation plans, but much more effort is still needed.
Research has shown that the magnetic free energy stored in the corona, quickly discharged by magnetic reconnection, powers solar flares and CMEs (Priest & Forbes 2002). The process of building the coronal free energy is controlled by the structural evolution of the magnetic field on the photosphere where plasma dominates the process. Observing and measuring the structure and evolution of the photospheric magnetic field can provide valuable information and clues to the triggering mechanisms of flares and CMEs. There are many physical properties or parameters, as we will discuss later in the paper, that characterize the static photospheric magnetic field, such as integrated Lorentz force, magnetic helicity injection, unsigned magnetic flux, vertical electric currents, magnetic shear and gradient, and magnetic energy dissipation.
Researchers spent significant efforts attempting to understand the physical relationship between flare productivity and non-potentiality of active regions (ARs) as specified by the physical parameters. This led researchers to apply different methods to predict flares that are not based on physical models, but rather based on statistical modeling and machine learning (Barnes et al. 2016). Machine learning gives computer programs the ability to learn from data and progressively improve performance. It utilizes input data, also called training data, and learns hidden insights in the training data to build a predictive model that will be used later to make predictions on unseen test data.
In our previous work (Liu et al. 2017), we reported the results of solar flare prediction using the random forest (RF) algorithm in Breiman et al. (1984). We constructed a database of solar flare events considering the physical parameters provided by the Space-weather HMI Active Region Patch (SHARP), and categorized solar flares into four different classes, namely B, C, M and X, based on the X-ray flare catalogs available at the National Centers for Environmental Information (NCEI) 1 . We employed the RF algorithm and the physical parameters or features to perform multi-class classification of solar flares, predicting the occurrence of a certain class of flares in a given AR within 24 h.
In this paper, we extend our previous work in Liu et al. (2017) by considering two additional multi-class classification algorithms: multilayer perceptrons (MLPs) and extreme learning machines (ELMs). We implement these algorithms into a machine-learning-as-a-service (MLaaS) framework, called DeepSun, which allows scientists to perform multi-class flare prediction on the internet. Specifically, our work here makes two contributions.
- 1.We develop an ensemble (ENS) method for multi-class flare prediction that performs better than the existing machine learning algorithms including RF, MLP and ELM according to our experimental study.
- 2.We design and implement DeepSun, which is the first MLaaS system of its kind for solar flare prediction.
The rest of this paper is organized as follows. Section 2 describes the data and the SHARP predictive parameters used in this study. Section 3 describes the machine learning algorithms employed by DeepSun. Section 4 explains the methodology followed to evaluate the performance of these machine learning algorithms. Section 5 presents and compares the prediction results obtained from the machine learning algorithms. Section 6 details the design and implementation of the DeepSun framework. Section 7 surveys related work and compares DeepSun with existing computing systems providing similar services. Section 8 concludes the paper and points out some directions for future research.
2. Data and SHARP Parameters
In 2012, SHARP data were released. The main goal of the SHARP data was to facilitate AR event forecasting (Bobra et al. 2014). These data are available in the Joint Science Operations Center (JSOC) 2 as hmi.sharp series which includes magnetic measures and parameters for many ARs. In 2014, another data series, cgem.Lorentz, was produced based on the SHARP data. This series includes the Lorentz force estimations. The main goal of this series was to help diagnose the dynamic process of ARs. Bobra et al. (2014) considered 25 physical parameters in the SHARP datasets that characterize the AR magnetic field properties. The authors relied on a univariate feature selection method to score the 25 parameters, and suggested that the top 13 out of the 25 parameters be regarded as predictors for flare activity. Table 1 summarizes these 13 parameters and their descriptions. More details about the 13 magnetic parameters can be found in Liu et al. (2017). Following Bobra et al. (2014) and Liu et al. (2017) we use the same 13 SHARP parameters in the work presented here.
Table 1. Thirteen SHARP Parameters Used in Our Study
| Parameter | Description |
|---|---|
| ABSNJZH | Absolute value of the net current helicity |
| AREA_ACR | Area of strong field pixels in the active region (AR) |
| EPSZ | Sum of z-component of normalized Lorentz force |
| MEANPOT | Mean photospheric magnetic free energy |
| R_VALUE | Sum of flux near polarity inversion line |
| SAVNCPP | Sum of the modulus of the net current per polarity |
| SHRGT45 | Fraction of area with shear > 45° |
| TOTBSQ | Total magnitude of Lorentz force |
| TOTFZ | Sum of z-component of Lorentz force |
| TOTPOT | Total photospheric magnetic free energy density |
| TOTUSJH | Total unsigned current helicity |
| TOTUSJZ | Total unsigned vertical current |
| USFLUX | Total unsigned flux |
We constructed a database based on the SHARP parameters extracted from the solar images that are available at JSOC and the X-ray flare catalogs provided by NCEI (Liu et al. 2017). We consider the period between May 2010 and December 2016. We select and record 845 flares in this period, among which 128 flares are of class B, 552 flares are of class C, 142 flares are of class M and 23 flares are of class X where identified locations of the C-, M- and X-class flares are within about ± 70° of the central meridian (Liu et al. 2017). These 845 flares come from 472 ARs. The duration of a flare ranges from several minutes to hours. The duration of an AR ranges from days to months. If there are several flares from the same AR on the same day, the highest-class flare is recorded; if there are several highest-class flares on the same day, only the last such flare on that day is recorded. If two different ARs produce flares on the same day, the highest-class flare for each AR on that day is recorded separately. See section 2 of Liu et al. (2017) for more details on the criteria applied to select the 845 flares. Table 2 summarizes the flare information.
Table 2. Numbers of Flares and ARs per Solar Flare Class
| Flare Class | Number of Flares | Number of ARs |
|---|---|---|
| B | 128 | 88 |
| C | 552 | 281 |
| M | 142 | 88 |
| X | 23 | 15 |
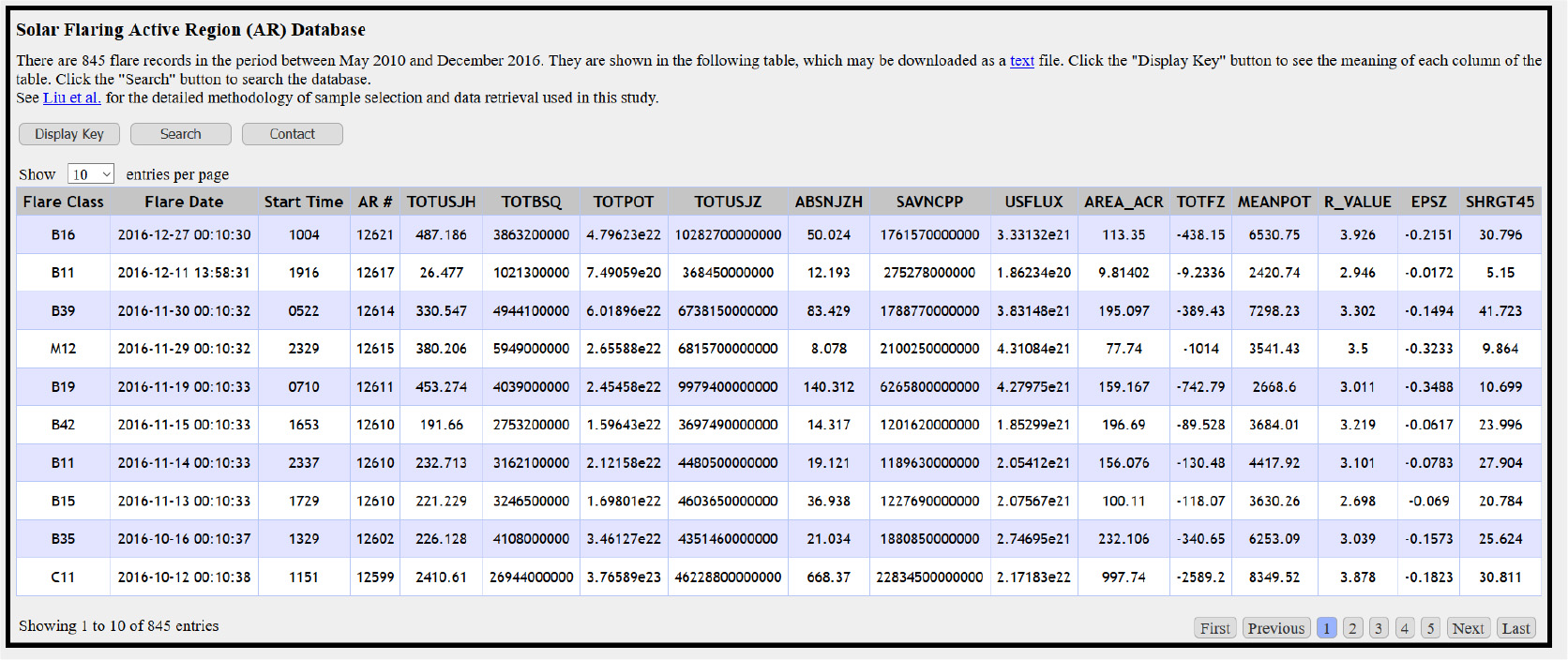
We created and stored 845 corresponding data samples (records) in our database, displayed in Figure 1 and accessible at https://nature.njit.edu/spacesoft/Flare-Predict/, where each data sample contains values of the 13 SHARP parameters or features listed in Table 1. Specifically, we created one data sample (record) for each flare. Thus, each record in our database has only one flare and corresponds to one date. The "Flare Date" column featured in Figure 1 indicates the first time on the flare date when all 13 SHARP parameter values are available, and the "Start Time" column indicates the start time of the flare on that date. Choosing SHARP parameter values measured at the beginning of the flare date is in accordance with our objective of predicting flares within 24 h. The two digits following a class label (B, C, M, X) are ignored in performing flare prediction. For simplicity, the two digits are specified without a dot (e.g., "B1.6" is specified as "B16").
Fig. 1 Screenshot featuring our online flare database.
Download figure:
Standard imageBecause the 13 SHARP parameters have different scales and units, we normalize the parameter values as follows. Let  (
( , respectively) denote the normalized (original, respectively) value of the ith parameter of the kth data sample. Then
, respectively) denote the normalized (original, respectively) value of the ith parameter of the kth data sample. Then

where maxi (mini , respectively) is the maximum (minimum, respectively) value of the ith parameter. The normalized values range from 0 to 1.
3. Machine Learning Algorithms
DeepSun employs three machine learning algorithms for flare prediction: RFs(Breiman et al. 1984), MLPs (Rosenblatt 1958; Braspenning et al. 1995) and ELMs (Huang & Chen 2007, 2008). RF is a tree-based algorithm comprised of multiple binary classification and regression trees (CARTs) while both MLP and ELM are feed-forward artificial neural networks (ANNs; Braspenning et al. 1995). All the three algorithms are well suited for multi-class classification. In addition, we develop an ENS algorithm, which works by taking the majority vote of RF, MLP and ELM. When there is no majority vote for a test data sample, the ENS algorithm returns "no-verdict". Since there are three machine learning algorithms, this "no verdict" case occurs when the three algorithms assign the test data sample to three different classes.
We implemented the machine learning algorithms in Python leveraging the scikit-learn package (Pedregosa et al. 2011). Each algorithm has different optimization parameters to be tuned based on the training and test datasets. Our RF algorithm, which is the same as the one used in Liu et al. (2017), is composed of 1000 trees. We set the number of randomly chosen features to six when splitting a node to build a tree. The configurations and parameter settings of the MLP and ELM algorithms are described in detail below 3 . The parameter values were chosen to optimize the performance of each algorithm.
3.1. Multilayer Perceptrons
MLP is a variation of the single perceptron model originally introduced by Rosenblatt (1958). MLP consists of at least three layers: an input, an output, and one or several hidden layers. The number of hidden layers is a configuration parameter that can be adjusted by the user. MLP is a multi-class learning algorithm that can be applied for non-linearly separable problems. Each node, except the input nodes, is a neuron that incorporates a non-linear activation function. It utilizes back-propagation to calculate the weights used in the network's activation function.
The MLP algorithm generally works as follows. We create weighted connections from each node in the input layer to each node in the first hidden layer h1. The process is repeated to create connections from subsequent hidden layer hi to hi + 1 until hL where L is the total number of hidden layers. The connection from a node in a source layer, si , to a node in a target layer, ti , is created with a weight wi to generate a weighted sum that is passed to the next connection through the activation function. The weights of the connections are adjusted based on corrections that minimize the error in the entire output to produce the final result. We use the rectified linear unit (ReLU; Nair & Hinton 2010) as the activation function and optimize the log-loss function utilizing stochastic gradient descent where the log-loss is also known as the crossentropy loss function. Most of the parameters in our MLP model are set with the default values provided by the scikitlearn library in Python (Pedregosa et al. 2011) except that the number of hidden layers is set to 200, the number of neurons in each hidden layer is set to 150, the learning rate is set to 0.001 and the batch size is set to 200.
3.2. Extreme Learning Machines
ELM is a classification, regression and clustering algorithm that works for generalized single hidden layer feed-forward networks (Huang & Chen 2007, 2008). It has input, output and single or multiple hidden layers where hidden nodes' parameters do not need to be tuned. The parameters of the hidden nodes can randomly be assigned with non-linear transforms or inherited from their ancestors without being updated. In most cases, the output weights of ELM are learned in a single step which tends to be a linear model. ELM often has better scalability with a much faster learning speed.
The ELM algorithm generally works as follows. We determine the transfer function (activation function), the number of hidden layers, which is set to 1, and the number of neurons, which is set to 200, in the hidden layer. Then we assign weights and biases of neurons in the input layer where no tuning is needed. Finally we calculate the output weights. In our ELM model, we utilize the hyperbolic tangent (tanh) as the activation function and use the cross-entropy loss function with a regularized least squares solver.
4. Performance Evaluation Methodology
We conducted a series of experiments to evaluate the performance of the machine learning algorithms presented in Section 3 considering two types of datasets. The first type of dataset, referred to as original datasets, was obtained by duplicating the database described in Section 2 to create 100 identical copies of the database where each copy was an original dataset. Each original dataset contained 128 B-class, 552 C-class, 142 M-class and 23 X-class flares where each flare corresponded to a record in the dataset. There were 845 flares and hence 845 records in each original dataset. Totally there were 100 original datasets. In addition, to mitigate the class imbalance problem that poses a major challenge in machine learning (see, e.g., Japkowicz & Stephen 2002), we created the second type of dataset, referred to as modified datasets, by randomly selecting 142 unique C-class flares from the total of 552 C-class flares. To avoid any bias, we repeated this random selection 100 times, so we ended up with 100 modified datasets, where each modified dataset contained 128 B-class, 142 C-class, 142 M-class and 23 X-class flares. Due to the few X-class flares, the modified datasets were still imbalanced datasets though they were not as unbalanced as the original datasets.
We used 10-fold cross validation in which for each dataset, we randomly shuffled to create 10-fold partitions using the KFold function provided by the scikit-learn library in Python (Pedregosa et al. 2011). Each machine learning algorithm was trained by nine of the 10 folds, and the 10th fold was used for testing. Notice that because the 10 folds in each original dataset were created randomly, the prediction results obtained from the 100 original datasets were different even though the 100 original datasets were identical. Notice also that each data sample (i.e., each record in our datasets) corresponded to one date and contained one flare. Each data sample either belonged to the training dataset or belonged to the testing dataset. There was no data sample belonging to both training and testing datasets. Thus, the testing data were not seen during training. To further reduce the errors associated with cross validation, we repeated the 10-fold cross validation procedure 100 times for each of the 100 original (modified, respectively) datasets, which resulted in 10 000 tests for the original (modified, respectively) datasets. The average values obtained from the 10 000 tests were calculated and reported.
In assessing the performance of the algorithms, we converted the multi-class classification problem at hand into four binary classification problems for the four classes B, C, M and X respectively. For example, consider the binary classification problem for class B in a dataset. Here, we say a data sample is positive if it is in class B, or negative if it is not in class B, i.e., it is in class C, M or X. We define true positive (TP), false positive (FP), true negative (TN) and false negative (FN) as follows. TP is a data sample where an algorithm predicts the data sample to be positive and the data sample is indeed positive. FP is a data sample where the algorithm predicts the data sample to be positive while the data sample is actually negative. TN is a data sample where the algorithm predicts the data sample to be negative and the data sample is indeed negative. FN is a data sample where the algorithm predicts the data sample to be negative while the data sample is actually positive. We also utilize TP (FP, TN and FN respectively) to represent the number of true positives (false positives, true negatives and false negatives respectively).
Because we are tackling imbalanced classification problems, we adopt two performance metrics, balanced accuracy (BACC; Brodersen et al. 2010) and true skill statistics (TSS; Hanssen & Kuipers 1965). BACC is defined as follows

and TSS is defined as follows

BACC considers both sensitivity (also known as the true positive rate or recall) and specificity (also known as the true negative rate). It calculates the accuracy in the positive dataset and in the negative dataset separately, and is especially useful when the datasets are imbalanced, i.e., one dataset has many more elements than the other. In addition, because of its unbiasedness over the class-imbalance ratio (Woodcock 1976), we follow the suggestion of Bloomfield et al. (2012) to use the TSS score, which is the recall subtracted by the false alarm rate. We obtain BACC and TSS for each binary classification problem. There are four binary classification problems.We then calculate the average of the BACC and TSS values obtained from the four classification problems, and take the average as the result for the multi-class classification problem.
5. Prediction Results
Table 3 (Table 4, respectively) compares the BACC and TSS values of the four machine learning algorithms presented in Section 3 for each binary classification problem and for the overall multi-class classification problem relying on the original (modified, respectively) datasets. In these tables, the highest performance metric values are highlighted in boldface. It can be seen from the tables that the proposed ENS algorithm outperforms the existing algorithms RF, MLP and ELM in both the original and modified datasets. Furthermore, the results from the modified datasets are better than those from the original datasets. This is due to the fact that the modified datasets have more balanced class distributions than the original datasets in the sense that the ratio of the number of X-class flares to the number of C-class flares is higher in the modified datasets than in the original datasets. It is worth noting that the performance of all the algorithms degrades in predicting X-class flares. This probably happens because the X class has much fewer flares than the other classes, and hence the algorithms cannot gain enough knowledge about the X-class flares. Overall, there were approximately less than 2% of data samples receiving "no verdict" in both the original and modified datasets.
Table 3. Flare Prediction Results Using 13 SHARP Parameters and Four Machine Learning Algorithms on Original Datasets
| Class B | Class C | Class M | Class X | Average | |
|---|---|---|---|---|---|
| BACC | |||||
| ENS | 0.659 | 0.635 | 0.618 | 0.610 | 0.631 |
| RF | 0.635 | 0.630 | 0.590 | 0.580 | 0.608 |
| MLP | 0.616 | 0.620 | 0.584 | 0.575 | 0.599 |
| ELM | 0.629 | 0.619 | 0.586 | 0.573 | 0.601 |
| TSS | |||||
| ENS | 0.318 | 0.269 | 0.236 | 0.220 | 0.261 |
| RF | 0.271 | 0.259 | 0.179 | 0.160 | 0.217 |
| MLP | 0.231 | 0.241 | 0.169 | 0.150 | 0.198 |
| ELM | 0.259 | 0.238 | 0.172 | 0.146 | 0.204 |
Table 4. Flare Prediction Results Using 13 SHARP Parameters and Four Machine Learning Algorithms on Modified Datasets
| Class B | Class C | Class M | Class X | Average | |
|---|---|---|---|---|---|
| BACC | |||||
| ENS | 0.871 | 0.691 | 0.790 | 0.670 | 0.756 |
| RF | 0.834 | 0.663 | 0.749 | 0.645 | 0.723 |
| MLP | 0.818 | 0.659 | 0.757 | 0.599 | 0.708 |
| ELM | 0.791 | 0.641 | 0.721 | 0.608 | 0.690 |
| TSS | |||||
| ENS | 0.745 | 0.380 | 0.551 | 0.362 | 0.507 |
| RF | 0.708 | 0.378 | 0.537 | 0.330 | 0.488 |
| MLP | 0.661 | 0.285 | 0.526 | 0.010 | 0.371 |
| ELM | 0.618 | 0.296 | 0.446 | 0.227 | 0.397 |
6. The DeepSun Framework
6.1. System Design
The four machine learning algorithms (ENS, RF, MLP, ELM) presented in Section 3 have been implemented into our DeepSun system where the algorithms are utilized as a back-end, also known as the server-side, engine for the MLaaS platform. Figure 2 presents the overall architecture of the DeepSun framework. The system supports two different types of users: web and programming. The web user invokes the service by accessing a graphical user interface (GUI) to perform flare predictions. The programming user can utilize any programming language that supports HTTP requests, such as Java, C++, Python, Node.js, JavaScript modules in React or other frameworks to perform flare predictions.
Fig. 2 Overview of DeepSun.
Download figure:
Standard imageMLaaS is a representational state transfer (REST) application programming interface (API) that supports JavaScript Object Notation (JSON) formatted payloads in the request and response. JSON is a plain-text and lightweight data-interchange format. It is structured with attributes and values in an easy way for humans to read and write. JSON is language independent but it is easy to parse; therefore almost every programming language supports it. The request transmits the user's data from the front-end to the back-end and must include well defined JSON formatted test data to predict or training data to create a predictive model. The response transmits the result from the back-end to the front-end, which is a well formatted prediction result or the predictive model identifier. Here, the front-end means the client-side that can be a web-designed interface for the web user or a program for the programming user.
6.2. System Implementation
When a user visits DeepSun's home page, the user sees three options. Option 1 allows the user to select the pretrained models provided by DeepSun. Option 2 enables the user to upload his/her own training data to create his/her own machine learning models for solar flare prediction. Option 3 allows the user to perform solar flare prediction using RESTful services. Figure 3 features DeepSun's home page, which can be accessed at https://nature.njit.edu/spacesoft/DeepSun/.
Fig. 3 Screenshot depicting the home page of DeepSun.
Download figure:
Standard image6.2.1. Pretrained models in DeepSun
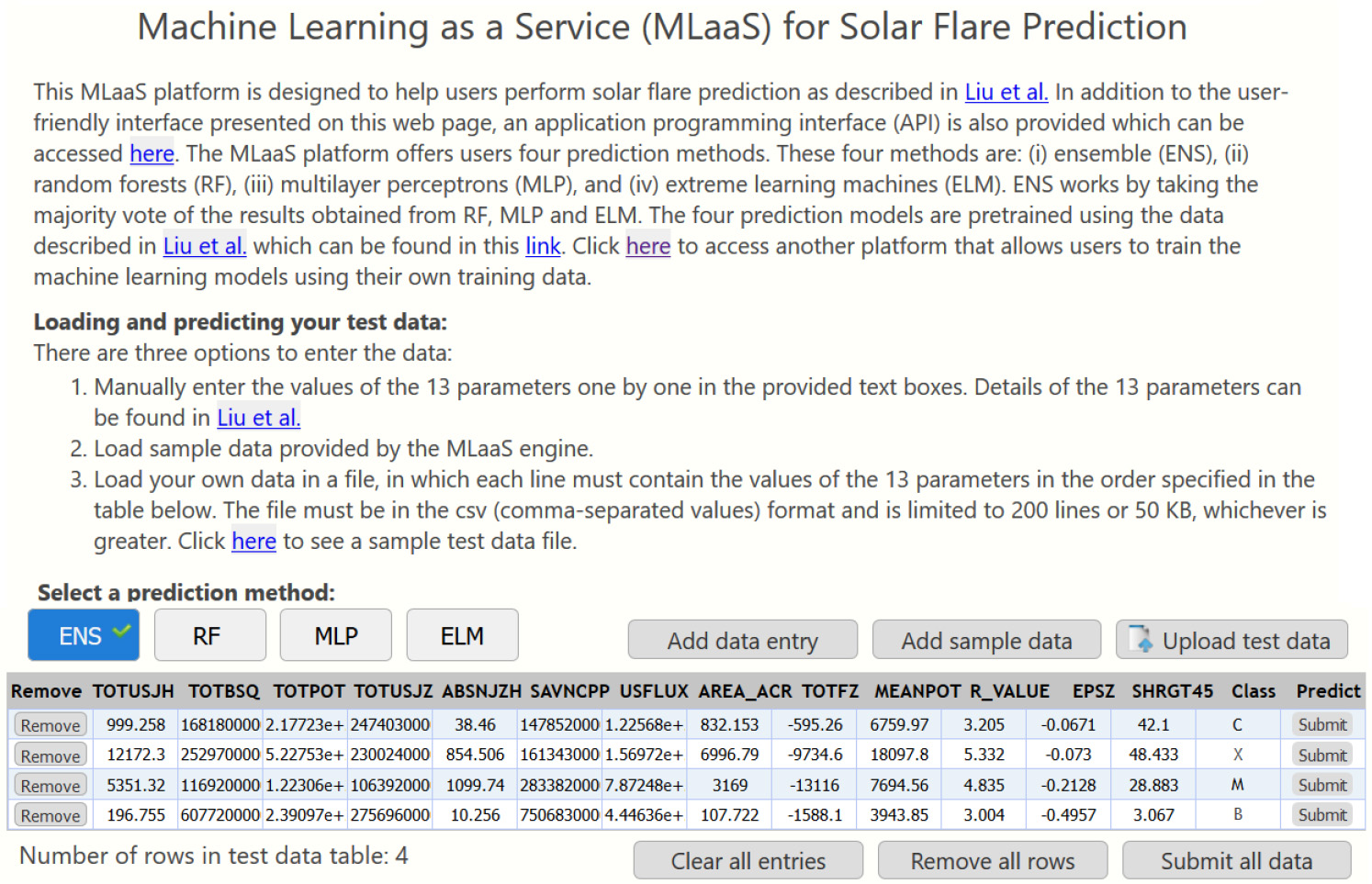
The pretrained models are ready-to-use models that were created utilizing the database described in Section 2. With the pretrained models, a user has three options to load test data samples containing the 13 SHARP parameters or features listed in Table 1: (1) Manually enter the data samples with values of the 13 SHARP parameters one by one in the provided text boxes. (2) Load sample data provided by the DeepSun engine. (3) Load the user's own data in a file, in which each line contains the values of the 13 SHARP parameters. The user may invoke the services to predict all the loaded, or entered, test data at once or make predictions one by one. Figure 4 displays the webpage of pretrained models on which four predictions were made using the ENS algorithm.
Fig. 4 Screenshot showing the webpage with pretrained models of DeepSun.
Download figure:
Standard image6.2.2. Custom models in DeepSun
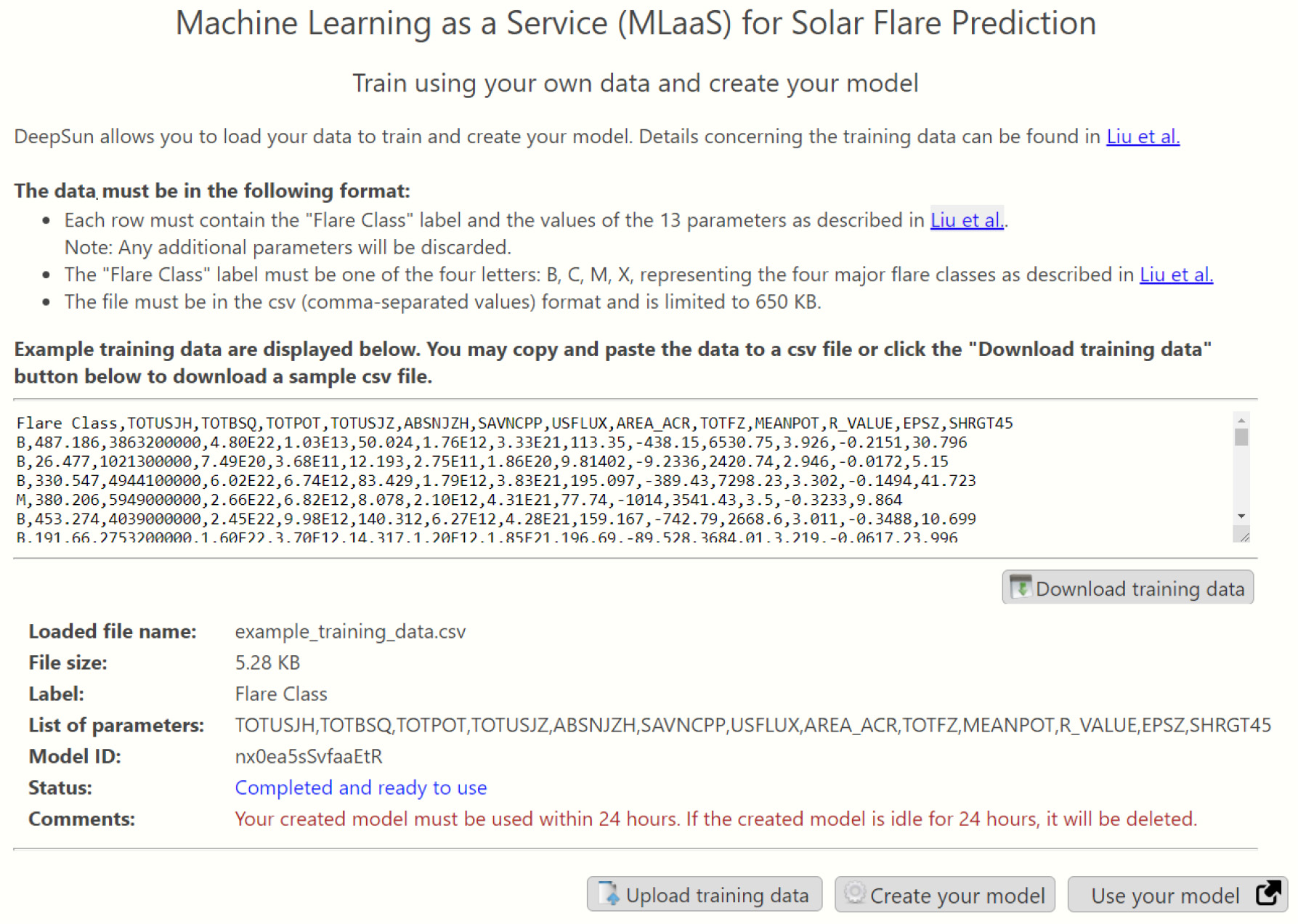
DeepSun allows the user to load his/her data to train and create his/her custom model to predict solar flares. The training data are saved in a file meeting DeepSun's format requirement. When the user creates a custom model, a model identifier (id) is assigned to the current session. If the created model is idle for 24 h, it will be deleted. Once the model is ready, the user goes to DeepSun's GUI with the assigned model id to perform flare predictions as done with the pretrained models. The model id is used to distinguish between the custom model and pretrained models. Figure 5 shows the webpage of custom models with example training data displayed.
Fig. 5 Screenshot displaying the webpage with custom models of DeepSun.
Download figure:
Standard image6.2.3. RESTful API for DeepSun
Representational state transfer (REST) is an architectural style that defines rules for creating web services for an API. A web service application that implements and conforms to the REST architecture is referred to as a RESTful application. The RESTful application allows the user to interact with its system using http requests to access the data of the system in a well-defined format. Our RESTful API uses JSON, which is a lightweight format for storing and transmitting plain text data as described in Section 6.1.
The RESTful API helps the programming user perform solar flare predictions relying on the pretrained or custom models. The API supports the POST request to predict solar flare occurrence or create a custom model, and the GET request to get a random data sample from our training database. The interface supports JSON formatted strings for requests' body and their result. The interface also supports two different debug levels; they are (i) INFO which is the default debug mode and (ii) DEBUG to return additional data with the result.
The return result from the POST request is a JSON object including the predicted solar flare occurrence and its class. Each test data sample is associated with a JSON object that includes two attributes. One attribute is "fcnumber" which is the numerical representation for the solar flare class where we define "1" ("2", "3", "4" respectively) to represent class B (C, M, X respectively). The other attribute is "fcname" which is the solar flare class name.
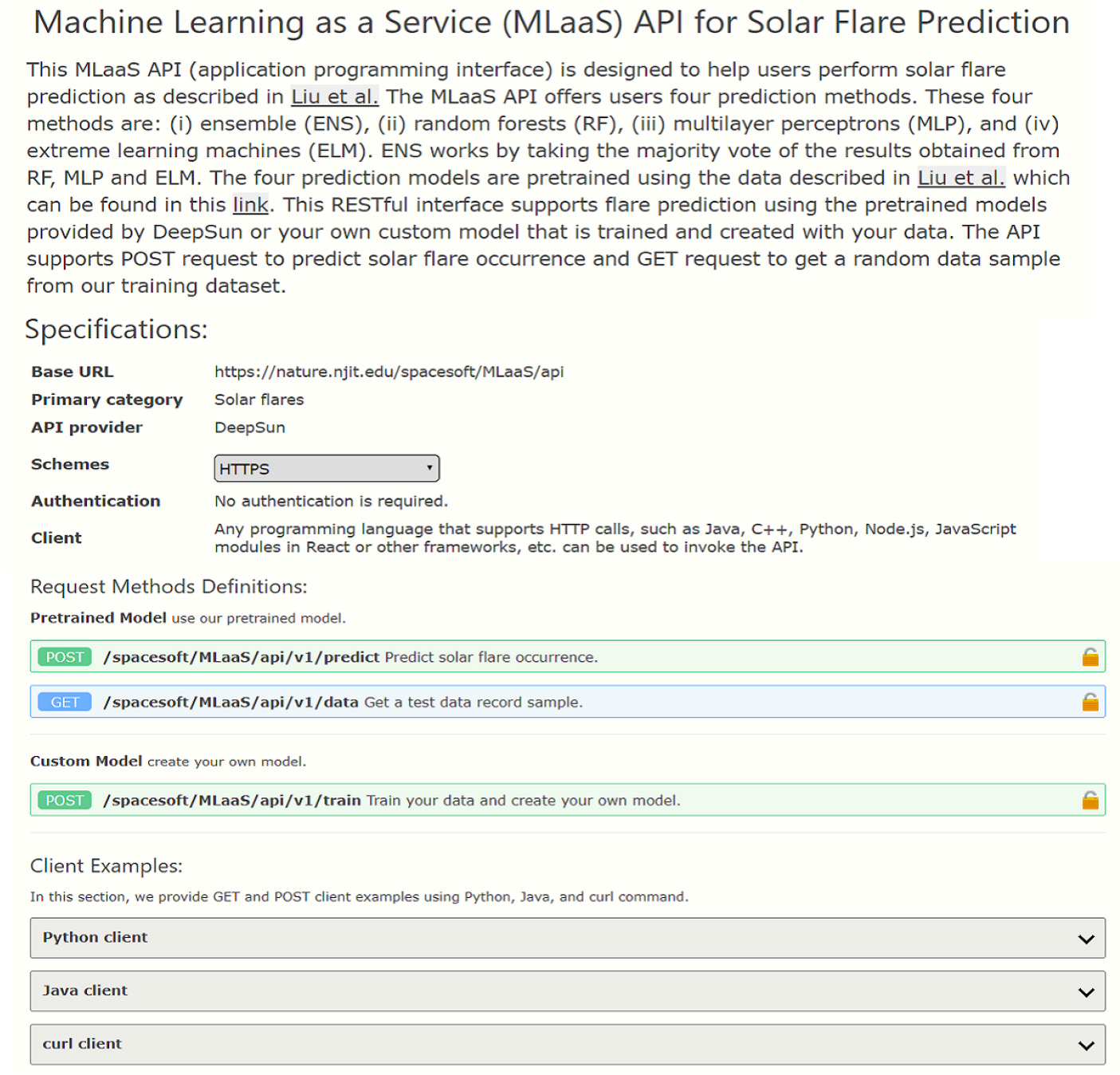
In addition, the RESTful API utilizes the POST request to create a custom model. The body of the request must be JSON formatted strings for an array of JSON objects. Each object must contain the 13 SHARP parameters and its flare class label where the label must be one of B, C, M or X. The return result of this POST request is a JSON object that contains the custom model identifier (id) which can be exploited for flare prediction. The custom model includes all the four algorithms (ENS, RF, MLP, ELM). Since the API is a RESTful interface, any programming language that supports HTTP calls, such as Java, C++, Python, Node.js, JavaScript modules in React or other frameworks, can be used to invoke the API. Figure 6 depicts the RESTful API page on which the definitions of the available methods and client examples are displayed.
Fig. 6 Screenshot showing the RESTful API page of DeepSun.
Download figure:
Standard imageWe present a simple Python program for invoking the RESTful API to get a data sample (record) as shown in Listing 1 followed by another Python program to perform solar flare prediction as featured in Listing 2. More example programs can be found on our API main page accessible at http://nature.njit.edu/spacesoft/MLaaS/api.
Listing 1 Python Program to Get a Data Sample Using the DeepSun RESTful API,
- 1.# import the requests library
- 2.import requests
- 3.# api-endpoint including the query parameter
- 4.URL = "https://nature.njit.edu/spacesoft/MLaaS/api/v1/data?query=getsampledata"
- 5.# sending get request and saving the response as response object
- 6.r = requests.get(url = URL)
- 7.# saving data in json format
- 8.data = r.json()
- 9.print(data)
Listing 2 Python Program to Perform Solar Flare Prediction Using the DeepSun RESTful API
- 1.# import the requests and simplejson modules
- 2.import requests
- 3.import simplejson as json
- 4.# defining the api-endpoint
- 5.API_ENDPOINT = "https://nature.nji.tedu/spacesoft/MLaaS/api/v1/predict"
- 6.# payload in JSON format data to be sent to api
- 7.# NOTE JSON is not python format; dumps and then loads, makes it JSON format
- 8.payload = '"parameters":"TOTUSJH":2699.42,"TOTBSQ":58985000000,"TOTPOT":1.07e+24,'
- 9.payload = payload + '"TOTUSJZ":53457900000000,"ABSNJZH":47.02,'
- 10.payload = payload + '"SAVNCPP":4510260000000,"USFLUX":3.58771e+22,'
- 11.payload = payload + '"AREA_ACR":1511.12,"TOTFZ":-3175.7,"MEANPOT":15255.1,'
- 12.payload = payload + '"R_VALUE":4.482,"EPSZ":-0.1021,"SHRGT45":49.982'
- 13.payload = json.dumps(payload)
- 14.payload = json.loads(payload)
- 15.print(payload)
- 16.# sending post request and saving response as response object
- 17.r = requests.post(url = API_ENDPOINT, data = payload)
- 18.print(r)
- 19.# saving response text
- 20.result=r.json()
- 21.print(result)
7. Related Work
There are two groups of work that are closely related to ours. The first group is concerned with solar flare forecasting. Many studies in this group used parameters derived from the line-of-sight (LOS) component of the photospheric magnetic field and produced probability outputs for the occurrence of a certain magnitude flare in a time period (Liu et al. 2017). Some researchers (e.g., Gallagher et al. 2002) relied on sunspot classification and Poisson statistics to provide probabilities for an AR to produce flares with different magnitudes within 24 h. Song et al. (2009) used three LOS magnetic parameters together with the ordinal logistic regression (OLR) method to predict the probabilities of a one-day flare. Bloomfield et al. (2012) suggested that the prediction probabilities should be converted into a binary (i.e., yes-or-no) forecast before they can be translated as flare-imminent or flarequiet. Following this suggestion, Yuan et al. (2010) employed support vector machines (SVMs) to obtain a clear true or false flare prediction for different flare classes.
On the other hand, the full vector data provide more information about the photospheric magnetic field structure compared to the LOS field. This type of information may provide better flare prediction performance, but due to the limitation imposed by ground-based vector magnetic field observations, the work on flare forecasting is limited. For example, Leka & Barnes (2003) utilized a small sample of vector magnetograms from the Mees Solar Observatory and applied a discriminant analysis to differentiate between flare-producing and flare-quiet ARs within a few hours. The authors later extended their work and used a larger number of samples with a 24- hr prediction window to generate probabilistic forecasts (Barnes et al. 2007).
Since May 2010, the Helioseismic and Magnetic Imager (HMI) onboard the Solar Dynamics Observatory (SDO) has been producing high quality photospheric vector magnetograms with high-cadence and full-disk coverage data (Bobra & Couvidat 2015). Relying on these data, Bobra & Couvidat (2015) calculated a number of magnetic parameters for each AR. They selected 13 from all the available parameters and achieved good prediction performance utilizing an SVM method for flares greater than M1.0 class. Nishizuka et al. (2017) applied a number of machine learning algorithms to HMI data and produced prediction models for ≥M and X-class flares with reasonably high performance. More recently, we employed a long short-term memory network for flare prediction (Liu et al. 2019).
The second group of related work is concerned with services computing. Benmerar et al. (2018) developed a brain diffusion magnetic resonance imaging (MRI) application to overcome the software-as-a-service (SssS) limitations caused by intensive computation. The application provides APIs that tackle browser paradigms to reduce the parallel computation rendered in the client side of the browser.
Wu et al. (2018) developed an automated testing technique to detect cross-browser compatibility issues so that they can be fixed. These cross-browser issues cause problems for an organization to create JavaScript web applications. The authors employed an existing recordand- play technique, Mugshot (Mickens et al. 2010), to design an incremental cross-browser incompatibility algorithm. The system starts off by injecting the record library into the browsers, collects traces and events to be replayed, and runs the detection algorithm to find different types of incompatibilities among the browsers.
Song et al. (2012) presented a machine learning algorithm for IT support services to automate the problem of determination and classification, and also find the root cause of such a problem. The algorithm is an online perceptron that learns about the user's problems from the data that were generated from logs and monitors information across different systems. The algorithm then categorizes the problems by finding the actual root cause from what it learned from the data. The algorithm employs an incremental learning technique and is able to automatically adjust the classifier parameters.
Li et al. (2018) described a new software documentation recommendation methodology that adopts a learn-to-rank (LTR) technique. LTR is an application of supervised and semi-supervised machine learning techniques. Their strategy combines the social context from a question-and-answer online system and the content of official software documentation to build the LTR model to provide accurate and relevant software documentation recommendations. Their experimental results demonstrated that this approach outperforms traditional code search engines including the Google search engine.
Our DeepSun system differs from the above works in two ways. First, DeepSun provides services dedicated to solar flare prediction, which has not been addressed by the existing services computing systems. Second, in the solar flare forecasting area, DeepSun is the first MLaaS system, to our knowledge, that allows scientists to perform multi-class flare predictions through the internet.
8. Conclusions and Future Work
We present an MLaaS framework (DeepSun) for solar flare prediction. This framework provides two interfaces: a web server where the user enters the information through a GUI and a programmable interface that can be used by any RESTful client. DeepSun employs four machine learning algorithms, namely the RF, MLP, ELM and ENS algorithms. Our experimental results demonstrated good performance of the ENS algorithm and its superiority over the other three machine learning algorithms.
In our work, we rely on the database constructed in Liu et al. (2017), which contains 845 data samples belonging to four flare classes: B, C, M and X across 472 ARs. These data samples are unevenly distributed. Specifically, there are 128 B-class, 552 C-class, 142 M-class and 23 X-class flares where each flare corresponds to a data sample. To mitigate the class imbalance problem, we create modified datasets by randomly selecting 142 unique C-class flares from the total of 552 C-class flares. Balancing the data samples changes the flare occurrence frequency but provides better performance results as shown in Section 5. Our goal here is to gain a better understanding of the relative performance of the four machine learning algorithms in dealing with different imbalanced datasets. The models studied here are mainly used for scientific purposes, not for operations.
Because there are four flare classes, we perform four-class classification to predict which class of flares would occur within 24 h. In practice, it is likely that there is no flare within 24 hr. To handle this situation, we adopt a two-step method. In the first step, a test record is fed to a binary classification model, which is similar to the binary classification tools described in Liu et al. (2019). This binary classification model predicts whether or not there is a flare within 24 h. If the prediction outcome is "no", then the test record represents a non-flare event, meaning there is no flare within 24 h. If the prediction outcome is "yes", then we enter the second step where we feed the test record to the DeepSun tool presented here to further identify which flare class the test record belongs to. If the test record is classified into class B (C, M or X), then we predict there is a B (C, M or X) class flare within 24 h.
In the current work, we focus on data samples composed of SHARP parameters. The HMI aboard the SDO also produces continuous full-disk observations (solar images). In future work, we plan to incorporate these HMI images into our DeepSun framework and extend our previously developed deep learning techniques (Hu et al. 2018, 2020; Liu et al. 2020b) to directly process the images. We also plan to combine our recently developed deep learning algorithms using the SHARP parameters (Liu et al. 2019) with the image-based techniques and machine learning algorithms described in this paper for more accurate solar flare prediction.
Acknowledgements
We thank the referee for very helpful and thoughtful comments. We also thank the SDO/HMI team for producing vector magnetic field data products. The X-ray flare catalogs were prepared by and made available through NOAA NCEI. This work was supported by U.S. NSF grants AGS-1927578 and AGS-1954737. C.L. and H.W. acknowledge the support of NASA under grants NNX16AF72G, 80NSSC18K0673 and 80NSSC18K1705.
Footnotes
- 1
In the NCEI catalogs, the B class is the lowest flare class (Liu et al. 2017).
- 2
- 3
The source code of the machine learning algorithms can be downloaded from https://web.njit.edu/~wangj/MLaaS.