Abstract
Previous series expansion studies of the magnetization and susceptibility of the Ising model are extended to the higher derivatives of the free energy with respect to the magnetic field. It is found that just above the critical temperature the 2nth derivative is given by
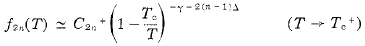
where in two dimensions γ = 1¾, Δ = 1fraction seven-eighths and in three dimensions γ = 1¼, Δ = 1fraction nine-sixteens. In two dimensions γ is exact and Δ is correct to 0.6%; the three-dimensional indices are correct to 0.2%. Just below the critical temperature
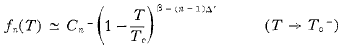
where in three dimensions 0.303 <or= β <or= 0.318 and 1·55 <or= Δprime <or= 1.65. If the even derivatives are to have the same index above and below Tc, then β = fraction five-sixteens and Δprime = 1fraction nine-sixteens. The latter index lies very close to the lower limit so that, although we cannot rule out Δprime = Δ, Δprime = 1fraction five-eighths is not unlikely. In two dimensions our results are consistent with linearity of the index and, if this is assumed, then β = fraction one-eighths and Δprime = 1fraction seven-eighths exactly and there is symmetry about Tc.
The amplitudes C2n+ and Cn- are estimated for n = 1 to 6.