Open Access
ARTICLE
Safety Assessment of Liquid Launch Vehicle Structures Based on Interpretable Belief Rule Base
1 Beihang University School of Automation Science and Electrical Engineering, Beijing, 100083, China
2 Beijing Aerospace Automatic Control Institute, Beijing, 100070, China
3 School of Computer Science and Information Engineering, Harbin Normal University, Harbin, 150025, China
4 Rocket Force University of Engineering, Xi’an, 710025, China
* Corresponding Author: Wei He. Email:
Computer Systems Science and Engineering 2023, 47(1), 273-298. https://doi.org/10.32604/csse.2023.037892
Received 20 November 2022; Accepted 03 March 2023; Issue published 26 May 2023
Abstract
A liquid launch vehicle is an important carrier in aviation, and its regular operation is essential to maintain space security. In the safety assessment of fluid launch vehicle body structure, it is necessary to ensure that the assessment model can learn self-response rules from various uncertain data and not differently to provide a traceable and interpretable assessment process. Therefore, a belief rule base with interpretability (BRB-i) assessment method of liquid launch vehicle structure safety status combines data and knowledge. Moreover, an innovative whale optimization algorithm with interpretable constraints is proposed. The experiments are carried out based on the liquid launch vehicle safety experiment platform, and the information on the safety status of the liquid launch vehicle is obtained by monitoring the detection indicators under the simulation platform. The MSEs of the proposed model are 3.8000e-03, 1.3000e-03, 2.1000e-03, and 1.8936e-04 for 25%, 45%, 65%, and 84% of the training samples, respectively. It can be seen that the proposed model also shows a better ability to handle small sample data. Meanwhile, the belief distribution of the BRB-i model output has a high fitting trend with the belief distribution of the expert knowledge settings, which indicates the interpretability of the BRB-i model. Experimental results show that, compared with other methods, the BRB-i model guarantees the model’s interpretability and the high precision of experimental results.Keywords
As the propulsion system of rocket vehicles and other space devices, liquid launch vehicles undertake essential tasks. The rocket structure, power plant, and control system constitute the three main parts of the liquid launch vehicle. Among them, the design of the arrow body is mainly composed of a tank structure and cabin structure, which belongs to a thin-walled cylinder [1]. It bears the sum of all the forces and support structures so that the various modules of the liquid launch vehicle are connected into a whole. If the safety of the arrow structure is threatened, it will cause severe damage to people’s lives and the national economy. Therefore, it is imperative to ensure the safe state of the liquid launch vehicle structure.
The safety assessment methods of the liquid launch vehicle can be generally divided into three kinds. (1) Black box model. It is a model that does not reveal its internal mechanisms and usually has high accuracy. However, the black-box model needs help understanding the reasons for data output, estimating the importance of each security assessment index to the assessment result, and understanding the interaction between different assessment indicators. For example, random forest [2]. (2) White box model. Such models are generally better interpretable, and their inner workings are easier to explain. However, simple models such as linear regression [3] and decision trees [4] tend to have limited predictive power and fail to model the inherent complexity of datasets, such as feature interactions. (3) Grey box model. It is a compromise model between the black box model and the white box model. This method of combining data and knowledge can maintain, to some extent, the interpretability and accuracy of the results of models such as belief rule base (BRB) [5].
Based on the improvement of the BRB model, a BRB-i model is proposed for the safety assessment of liquid launch vehicle structures. The proposed BRB-i model has the following advantages. First, the initialization, inference, and optimization processes of the BRB-i model are interpretable. The process can be traced, and the degree of human participation is high. Second, the BRB-i model can ensure the interpretability of the model while still guaranteeing the high precision of the results. Third, when the number of samples is small, the BRB-i model still performs well. The contribution points of this paper are as follows. (1) A whale optimization model with interpretability constraints is proposed. It can solve the problem that the parameters of the belief rule base lose interpretability after optimization. (2) A liquid launch safety assessment model based on BRB-i is proposed. The model ensures the accuracy of liquid launch vehicle safety assessment and the interpretability of the model.
The main structure of the paper is as follows. The first part presents the research content of the thesis. The second part introduces the related work and describes the research status and deficiency of the liquid launch vehicle safety state assessment model in detail. The third part proposes three critical problems to be solved in constructing the BRB-i model. The fourth part defines the interpretability criterion and describes in detail the safety evaluation model of the liquid launch vehicle arrow body based on BRB-i. In the fifth part, the BRB-i model is studied and verified by using the data monitored by the experimental platform. The sixth part summarizes the paper and suggests future work.
In recent years, many scholars have conducted extensive and in-depth research on the structural safety of liquid launch vehicles. For the structural safety of a liquid launch vehicle, other scenarios on the Internet of Things and big data can be referenced. For example, Tang et al. [6] proposed an intelligent charging and discharging strategy based on decision functions. Xu et al. [7] used blockchain technology, RSU-assisted Telematics authentication, and fundamental agreement protocol techniques. The following three types of related work are described in terms of liquid launch vehicle safety evaluation methods. The relevant piece is shown in Table 1.
The first method is related to research on the black box model. Lee et al. [8] proposed a safety state assessment method for liquid launch vehicle engines that fused fault factors and a Kalman filter. Based on the linear optimization model, the energy balance equation with fault factors is used, and the Kalman filter is developed. Park et al. [9] developed a safety state assessment method for liquid launch vehicles based on deep neural networks. The numerical model is used to assess the safety state of liquid launch vehicles under various abnormal indexes. Yu et al. [10] proposed a new safety assessment method for liquid launch vehicle engines based on an adaptive genetic algorithm to optimize the backpropagation neural network (BPNN). This method can predict the sensor data in real-time, compare the collected actual data with the projected data, and assess the safety state of liquid launch vehicle motor by threshold judgment mechanism.
The second method is the correlative research of the white box model. Although the process of the white box model can be traced and explained, the high precision of the model cannot be guaranteed. Therefore, compared with the black box model, there is less research on the white box model. Hong et al. [11] used UML models for reliability assessment. This method provides reliability evaluation results by analyzing the failure probability of different levels. Zhang et al. [12] proposed a robust white box model for the interpretability of online dynamic security assessment (DSA). This method can ensure the interpretability of DSA, and the model process can be traced. This scenario can also be referenced.
The third method is the correlative research of the grey box model. Osipov et al. [13] conducted a safety assessment of rocket accidents under explosion conditions and proposed a simplified physical model to trace the complex biological process. This model can correctly predict the parameters in the process by order of magnitude to establish the qualitative image of dangerous accidents. Zhu et al. [14] proposed a grey hierarchical analysis model for a solid rocket motor cleaning system. The model uses an analytic hierarchy process to construct a safety assessment index system and uses the grey comprehensive assessment method to assess the safety status of the solid rocket motor cleaning system.
Although the assessment results have high accuracy with the black-box model, the modeling process must be interpretable. However, the accuracy of the white box model is limited due to its complex internal structure and harsh external operating environment. Based on the above discussion, the safety assessment of the liquid launch vehicle body structure is more suitable for the grey box model.
Belief rule base [5] is a security assessment method proposed by Yang et al., which has been widely used in fault diagnosis, security assessment, risk assessment, and other aspects. Specifically, BRB is commonly used in the following two types of scenarios: (1) The BRB model is a model approximator. The output obtained by the BRB model approximates the actual value. From this perspective, the BRB model is a black box tool similar to a support vector machine (SVM) and random forest [15]. (2) BRB is an expert system. The structure and belief rules of BRB have a strong correlation with the natural system, which can reflect the inner principle of the existing system to a certain extent. From this perspective, the BRB model is both interpretable and accurate [16]. BRB can fuse small sample data and solve the problem of data uncertainty. Even in the case of small samples, BRB has strong nonlinear modeling ability and high modeling accuracy.
However, influenced by process parameters, the interpretability of the model may be damaged to some extent after the modeling and reasoning process. This requires the original BRB model to design an improved and interpretable optimization model driven by a mixture of data and knowledge. Therefore, this paper proposes a whale optimization algorithm (WOA) [17] with interpretable constraints and a safety assessment model of liquid launch vehicle body structure based on an interpretable belief rule base (BRB-i) after reasonably designing an interpretable modeling process and optimization process. The interpretability of BRB-i mainly focuses on the situation of BRB as an expert system, reflecting the degree of correlation between the natural system and the structure and rules of BRB. The BRB-i model was verified by the data collected from the laboratory wireless sensor monitoring platform.
Although the black-box model can have high accuracy, it cannot guarantee the transparency of the inference process. Although the white-box model can guarantee interpretability, it cannot guarantee the accuracy of the output results. To meet the requirements of both accuracy and interpretability, the safety assessment of liquid launch vehicle body structure is more suitable to use the gray-box model. The BRB-i model is improved based on the belief rule base as a gray box model. However, the construction of the BRB-i also requires a clear modeling and optimization process for the structural safety assessment of the liquid launch vehicle. The following problems must be solved to construct the BRB-i-based structure safety assessment model of the fluid launch vehicle bodies.
Problem 1: How to design a reasonable and interpretable safety assessment model for liquid launch vehicle body structure is the first problem to be solved. In the current research on BRB, there are few studies on the interpretable aspects of BRB. Suppose the structure safety assessment model of a liquid launch vehicle body based on BRB has good interpretability. In that case, it can maintain the optimal decision of a complex rocket system and provide more information about the structure of a liquid launch vehicle body. The construction process of the interpretable fluid launch vehicle structure safety assessment model can be described as the following nonlinear mapping function:
where

Problem 2: How to design an interpretable optimization model for the BRB parameters is the second problem to be solved. The structural safety assessment model of the initial liquid launch vehicle body based on BRB is interpretable. However, the current optimization algorithms for BRB only improve the model accuracy, not the interpretability. As a result, the interpretability of the initial BRB may be damaged in the optimization model, which is manifested in the problems such as the expert knowledge not being effectively utilized, the optimized parameters being unreasonable, and the optimized belief rule not the actual liquid launch vehicle body structure system. Therefore, it is necessary to design an optimization model that can improve the model’s accuracy while still maintaining interpretability. The optimization process of building the structure safety assessment model of a liquid launch vehicle body can be described as the following nonlinear function:
where
4 Structural Safety Assessment Model of Liquid Launch Vehicle Based on BRB-i
The interpretability of the BRB-based structural safety assessment model for liquid launch vehicles refers to the model’s ability to express the system’s behavior in an understandable way that facilitates an increased level of human-machine interaction. Specifically, it means that a. it is transparent in the process of model construction, and the structure of the model can be integrated into the design principle of the actual liquid launch vehicle and arrow structure system and the experience knowledge gained from long-term practice; b. the model is traceable in the reasoning process, keeping the rationality and transparency of the reasoning steps; and c. the model can keep the above characteristics from being destroyed in the optimization process, and the optimized parameters can still have the physical meaning and characteristics without conflict. All these are conducive to the interaction between people and the established model and improve the model’s credibility.
The safety and stability of liquid launch vehicle body structure are essential for space safety. The interform design of a liquid launch vehicle is significant for discovering the factors affecting the rocket’s safety in time and avoiding further danger. Expert knowledge can be used effectively in the liquid launch vehicle body structure safety assessment model, which is interpretable. The specialist knowledge base, inference engine, and optimization model constitute the structure safety assessment model of the liquid launch vehicle body. Among them, the proposed whale optimization model with interpretable constraints can maintain the rationality of the optimized parameters and fully use expert knowledge, which every expert recognizes. The overall structure of the BRB-i model is shown in Fig. 1.
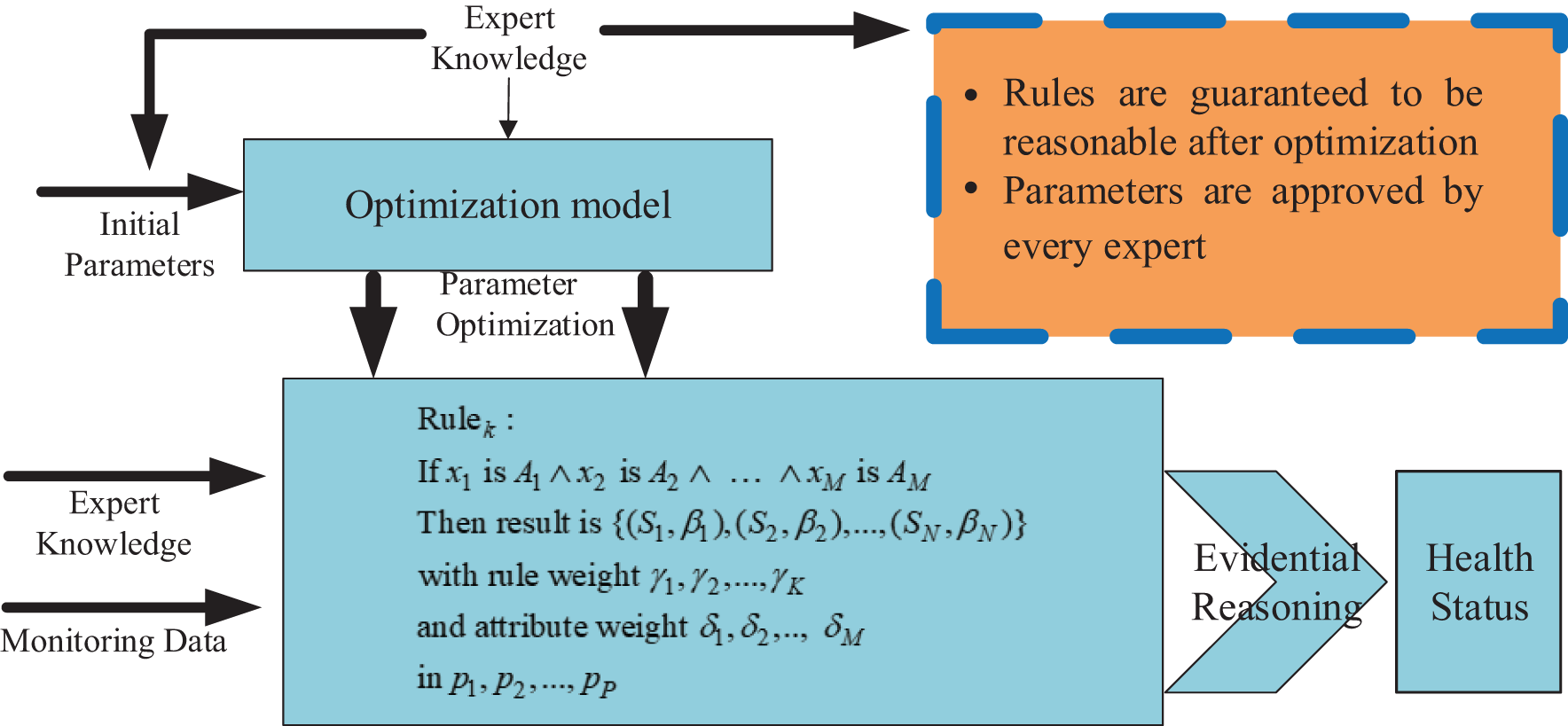
Figure 1: Overall structure of the BRB-i model
4.1 Construction of Interpretable Criteria
General interpretability criteria are elaborated in the literature [18]. Based on these criteria, the interpretability criteria based on the structural safety model of the liquid launch vehicle body are defined. Six criteria for the safety state assessment of a liquid launch vehicle are precisely defined, as shown in Fig. 2. The interpretability criteria of the structural safety assessment model for liquid launch vehicles are based on the following six criteria. First, Evaluate the completeness of indicators and results: When conducting a safety assessment of liquid launch vehicle structures, different assessment indicators will lead to different results. Therefore, the entirety of indicators and outcomes is essential. At least two referential values should be set for each assessment index, and at least one belief rule should be activated.
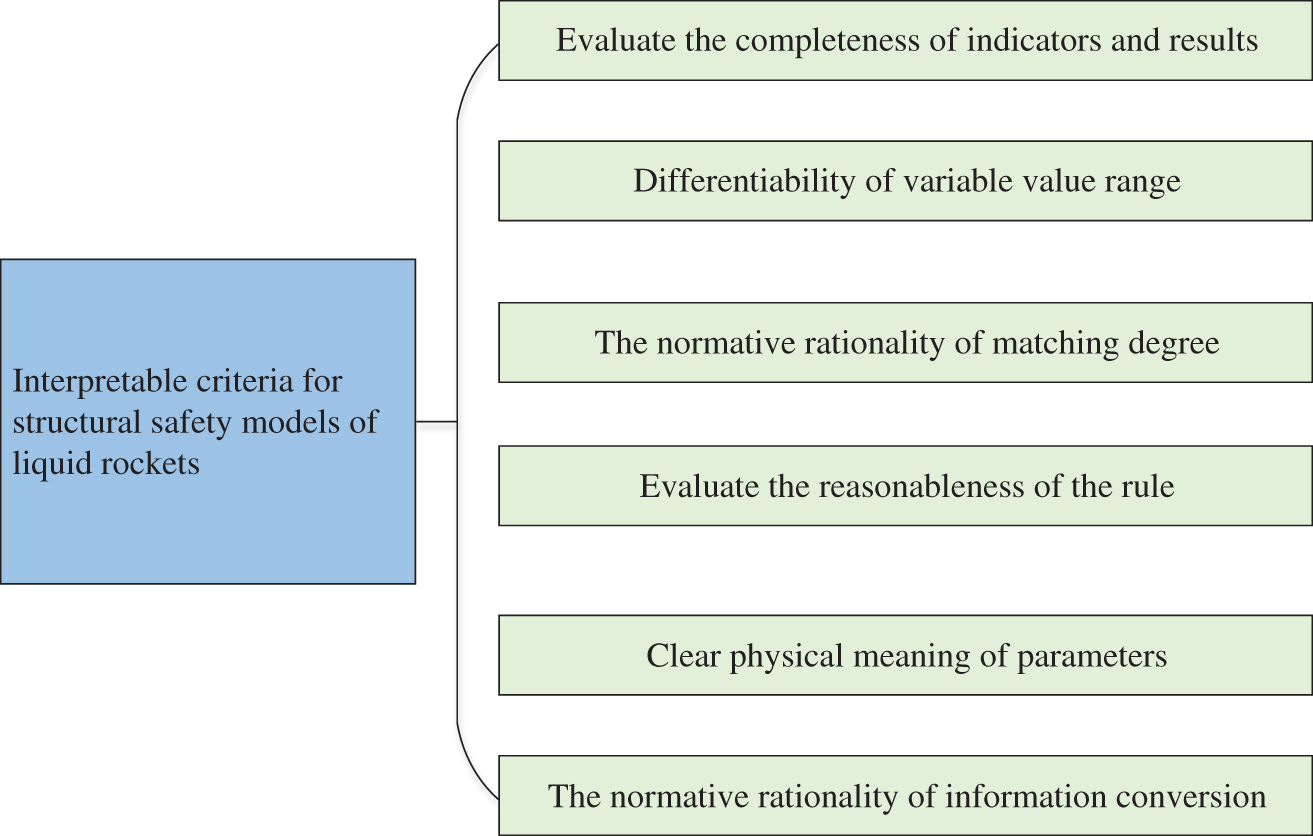
Figure 2: Interpretability criteria diagram
Second, when designing the structural safety assessment model for liquid launch vehicles, the referential value intervals of assessment indicators should be reasonably divided, and each spatial range should not overlap. In this way, the meanings corresponding to different fields can be distinguished from each other, which can ensure the interpretability of the model to some extent.
Third, for the normative rationality of the matching degree, in BRB, the sum of the matching degree of the referential value and the current input target assessment index data should be limited to the range of 0~1 so that it can meet the practical meaning.
Fourth, Evaluate the reasonableness of the rule. The reasonableness between the assessment indexes and the assessment results should be guaranteed when designing the liquid launch vehicle structural safety assessment model. Assuming that the expert knowledge is authoritative and reliable, setting the initial rule by expert knowledge can ensure the rule’s reasonableness. The reasonableness of the rules can be preserved when the model is optimized.
Fifth, the physical meaning of the parameters is clear. The reasoning process must be traceable and interpretable in constructing the liquid launch vehicle safety assessment model. This requires that each parameter that appears in the assessment process has a real physical meaning. The model parameters in the BRB species include rule weights, attribute weights, rule activation weights, belief levels, etc.
Sixth, normative rationality of information conversion. This interpretability criterion is developed to require that the characteristics of the original information are maintained in the conversion process. The rule- and utility-based method of converting pointer proposed by Yang can alter information reasonably wholly [19].
The BRB-i model is built on a set of “IF-then” rules that constitute an interpretable BRB-based assessment model. The relationship between the assessment index of the liquid launch vehicle structure safety assessment model and its safety state can be described as follows:
where
Compared with the traditional BRB, the BRB-i model defines interpretable criteria in the optimization process and adds interpretable constraints, which makes the model interpretable and more suitable for engineering applications.
The inference process of the BRB-i-based liquid launch vehicle structure safety assessment model consists of four steps. Firstly, the rule-matching degree needs to be calculated. Then, the rule activation weight is calculated. Next, the reasoner uses evidential reasoning (ER). Finally, the expected utility value is estimated to obtain the final assessment result. The reasoning process of the BRB-i model is as follows:
(1) Calculate the matching degree of rules. The rule matching degree is the difference between the input sample data information and the rule. This step should be calculated first. The calculation of rule matching degree is mainly to complete the transformation of input data. The change, including qualitative, quantitative, and symbolic attributes, is completed according to the different properties of the premise attributes [20]. The calculation is as follows:
where the matching degree of the assessment index to the
(2) The activation weight of the rule. In BRB, not all rules are equally important. Combining different attributes and different referential values generates each rule of BRB. Each government has a different meaning in the existing system, and the activation degree of the rule is also different. The activation weight of the rule is calculated as follows:
where the rule activation weight under the rule
(3) Use evidential reasoning to fuse activation rules [21]. Yang proposed the ER analytical method in 2007 as this step’s inference method, and the output’s belief distribution can be obtained after the rule fusion.
where the belief degree of the
where the output belief distribution set of BRB is denoted as
(4) Calculate the output utility value. The final output of the BRB model can be expressed as:
where
4.4 Optimization of BRB-i Model
Due to the complex environment of the existing flywheel system, the flywheel health state is greatly disturbed, and the healthy natural state is challenging to describe accurately. After the modeling and remodel’s parameters of the model may be destroyed by the optimization process, which violates the original intention of interpretability. Therefore, it is necessary to design an optimization algorithm that can improve the accuracy and be interpreted. BRB-i model is based on the whale optimization algorithm (WOA).
WOA is a metaheuristic optimization algorithm that simulates the hunting behavior of humpback whales. The main difference between the current work and other swarm optimization algorithms is the use of random or optimal search agents to simulate hunting behavior and the use of spirals to simulate the bubble net attack mechanism of humpback whales. This algorithm has the advantages of a simple mechanism, few parameters, and high search capability and can effectively cooperate with interpretable constraints. Therefore, this algorithm is chosen as the optimization algorithm for the proposed model.
Although the original WOA can improve the model accuracy, it still deviates from the interpretability in some parameters. This is reflected in the following: 1) The original WOA securely uses expert knowledge. The expert knowledge generated based on many practices is an essential source of the interpretability of the established model. Nevertheless, the original WOA algorithm scatters points randomly, which deviates from interpretability. 2) Some optimized rules cannot match the significance of the actual liquid launch vehicle structure safety system. The rules optimized by the optimization model should not conflict with the existing system. 3) Some optimized belief degrees are unreasonable and beyond the scope of practical significance. Therefore, it is necessary to improve the original WOA optimization algorithm to a certain extent to make it interpretable. The improved WOA optimization algorithm is shown in Fig. 3, and its process is as follows.

Figure 3: Flowchart of whale optimization algorithm with interpretable constraints
(1) Parameter initialization. The size of the humpback whale population is
(2) Set the scatter mode. This step abandons the random scatter mode of the original WOA algorithm and sets up a new scatter mode. The new method of scattering points is to scatter points near the expert knowledge, which can realize the effective use of the expert knowledge to realize interpretability. Suppose the current position of the humpback whale is denoted as
Among them, the belief degree of expert knowledge is
(3) Calculate the adaptive value of each humpback whale. The mean square error is denoted as the objective function and can be expressed as:
(4) Set interpretable constraints. Some parameters optimized by the original WOA deviate from the meaning of the existing system, and the improved WOA algorithm solves this problem by setting interpretable constraints. The specific constraints are as follows.
a. Limit the belief’s value range and obtain each expert’s approval. Expert knowledge is accumulating knowledge on the safety of actual liquid launch vehicle structures over a long period of practice. Assuming that expert knowledge is authoritative and information is reliable, the value of the belief degree should not violate expert knowledge and should be reasonably constrained [21]. This can be expressed as:
where the maximum and minimum values of belief approved by each expert are
b. Make the belief distribution in the optimized rule match with the existing system. The belief rule can reflect the relationship between the assessment index of liquid launch vehicle structure safety and its health state. In the original WOA algorithm, the optimized rules may not match the existing system, so it is necessary to set this constraint. This can be expressed as follows.
where
(5) Mobile operation. Mobile operation includes three parts: encirclement prey, foraging, and searching prey, which are as follows:
a. Surround the prey. Whales surround their prey by circling it, a behavior that can be described as follows:
where
where
b. Spiral bubble net foraging. The whale’s foraging behavior is a spiral bubble web, which swims toward prey in a spiral fashion, spitting bubbles as it goes. The behavior formula can express this behavior:
where
c. Search for prey. Humpback whales randomly search for prey based on each other’s location, which is described by the mathematical formula:
where
It can be seen from the above that the whale algorithm with interpretable constraints also improves the model accuracy and interpretability and is more reasonable in engineering applications.
4.5 Overview of Interpretability Based on the BRB-i Model
As an expert system, BRB can fully use qualitative knowledge and quantitative data in the modeling process and express uncertain information as a belief distribution. The safety assessment model of liquid launch vehicle structure based on BRB is interpretable in modeling and reasoning and can achieve good modeling results in the case of small samples. This section mainly discusses the interpretability of the structural safety model of a liquid launch vehicle body based on BRB from two aspects.
(1) Modeling interpretability. Expert knowledge based on long-term practice is an important source of interpretable modeling processes, so the interpretability of the knowledge base is particularly important. In BRB, a series of rules constitute a knowledge base. The interpretable knowledge base has a distinguishable semantic partition space, complete rules, a concise and easy-to-understand knowledge base, and precise parameter meaning [22].
(2) Interpretability of reasoning. The interpretability of the reasoning process is also very important. The structure safety model of a liquid launch vehicle based on BRB uses ER inference engine, and its interpretability is mainly reflected in the following: a. ER has good processing ability, and description ability for uncertain information in the form of belief distribution and has a clear explanation; b. ER can integrate uncertainty, update uncertainty with new information, and finally make decisions; c. Feasibility of the assessment process. Evidential reasoning has the ability to process multiple pieces of information simultaneously, such as natural language information, e.g., “If A and B, then C.” Qualitative judgments and quantitative uncertain data information can be combined by ER at the same time; d. Traceability of computational processes. The ER algorithm’s calculation process is straightforward, and every step can be traced and explained.
(3) Optimize interpretability. The BRB-i model proposes a new optimization algorithm with interpretable constraints, which clarifies the parameters’ meaning. The WOA optimization algorithm with interpretable constraints can make full and effective use of expert knowledge, make the actual system match the optimized belief distribution, and provide interpretability.
The primary purpose of this paper is to build a structural safety assessment model of a liquid launch vehicle body based on BRB with interpretability [23]. During the operation of a liquid launch vehicle, the skin and the propellant tank are two essential components critical to the rocket’s successful launch. This paper focuses on the structural safety assessment of these two components. As a kind walled shell, the impact of crustal vibration, airflow, temperature, and humidity on the structure is magnified during the launch phase and after the large tonnage of propellant filling, which makes it very easy for safety accidents to occur. Given this, this paper mainly focuses on the following possible safety hazards. The structure safety assessment index system of a liquid launch vehicle is shown in Fig. 4. The skin and propellant tank, as two crucial parts of a liquid launch vehicle body structure, are the main focus of this experiment [24]. During the rocket riser stage and propellant addition, the influence of crustal vibration, rocket inclination, temperature, and humidity on the structural safety of the liquid launch vehicle will be amplified, and safety accidents will quickly occur [25]. Therefore, this experiment will analyze these possible security risks.
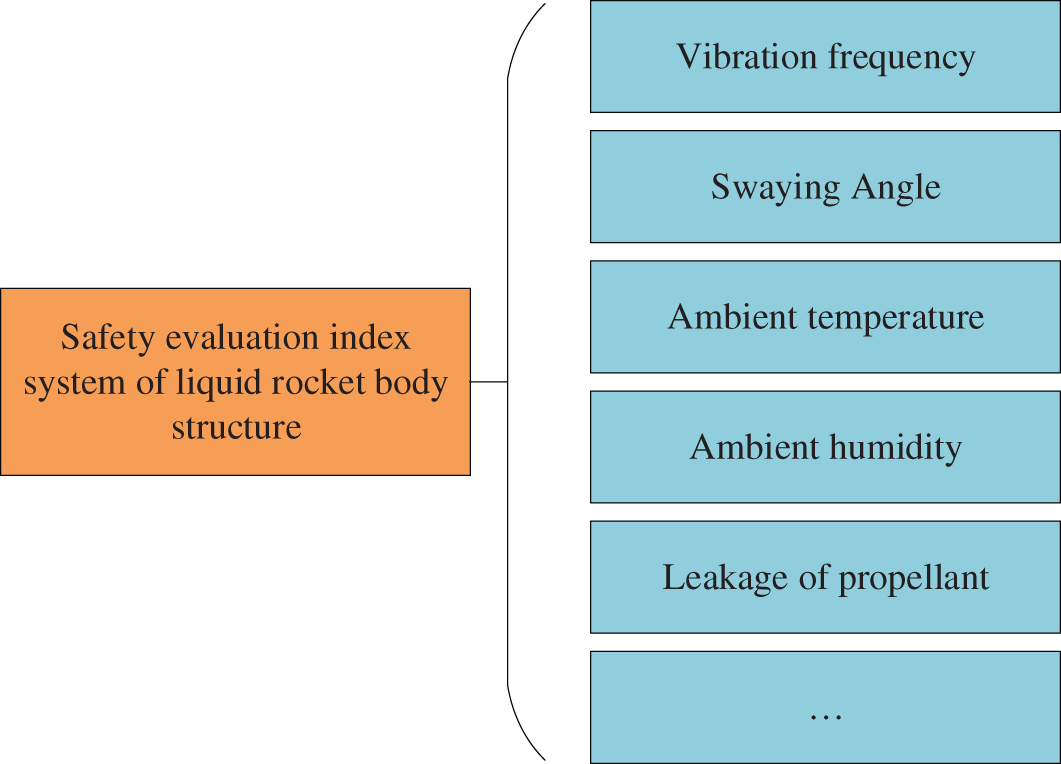
Figure 4: Index system for structural safety assessment of liquid launch vehicle
As highly sophisticated equipment with complex production and high price, the liquid launch vehicle performs complex tasks and has important political and economic significance for the country. As a complex equipment with special significance to national defense security, the liquid launch vehicle is sensitive to risk. It will cause serious damage to national security in case of danger. Therefore, the selection of data sets of liquid launch vehicles for their interpretable safety assessment is of great significance to national defense security.
The data in this experiment are from the wireless sensor platform monitoring built in the laboratory, and the natural environment is simulated through the simulation jammer. Since the ambient temperature and humidity are unchanged during the experiment and propellant leakage does not exist, only two indexes of vibration degree and inclination of the liquid launch vehicle are considered as assessment and monitoring indexes of the structural safety assessment model in this section. A total of 515 data samples were collected in this experiment, 450 of which were used as training samples for real-time adjustment and correction of model parameters. The remaining 65 were used as test samples. In addition, the initial setting of the optimization model is as follows: the population size is 20, the optimization dimension is 82, and the number of iterations is 800.
A large number of liquid launch vehicle failure samples are difficult to extract during the system life cycle, and the liquid launch vehicle failure samples under different failure modes are even more difficult to extract. This causes the problems of small sample sizes and unbalanced samples in the dataset. BRB, as an expert system that can fuse knowledge, has weaker dependence on data samples than data-driven methods and is suitable for datasets with small sample cases. Therefore, the resultant safety assessment model for liquid launch vehicles is improved based on BRB, which solves the problems of small sample sizes and unbalanced samples in liquid launch vehicle datasets.
5.1 Initialization of BRB-i Model
According to the liquid launch vehicle structure safety assessment model constructed above and based on the two assessment indexes of liquid launch vehicle vibration frequency and swaying angle, the belief rules are constructed as follows:
where



In addition, the rule weight and attribute weight in the initial model are set to 1. Combined with the reference level and referential value given in Tables 3–5, the initial model for structural safety assessment of the liquid launch vehicle and arrow body is shown in Table 6. The four actual safety states of liquid launch vehicles are given by field experts combined with the experience of long-term practice and reflect the probability of liquid launch vehicle accidents. According to the analysis of the safety state of the whole life of multiple batches and the same type of liquid launch vehicle, the experts give the relatively reasonable belief that distribution of the liquid launch vehicle in each state according to the actual use situation and the historical safety case. Expert knowledge is the accumulation of knowledge of liquid launch vehicles carried for a long time, and it is an essential source for interpreting the BRB expert system. The initial parameters of the model are set with expert knowledge, the real-time training data are used to adjust and modify these parameters, and the safety evaluation results are output. The interpretability of the model is reflected by the fitting degree of the output belief distribution and the initial belief distribution. The closer the two are, the stronger the interpretability of the model will be.

After the construction of the structure safety evaluation model of a liquid launch vehicle body based on interpretable BRB, the initial evaluation model will be affected by the actual working environment and working state of the rocket due to the ignorance and uncertainty of the expert knowledge. The accuracy of the model could be higher. Therefore, it is necessary to modify the model’s parameters to improve the evaluation model’s accuracy when evaluating the structural safety of liquid launch vehicles. The models with interpretable constraints added to the WOA optimization algorithm and projection covariance matrix adaptation evolutionary strategies (P-CMA-ES) [26] optimization algorithm will be denoted as BRB-i and PBRB-i, respectively. The fitting between the output results of the BRB-i and PBRB-i model and the real value is shown in Fig. 5, and the comparison diagram of the belief distribution of each rule is shown in Fig. 6.
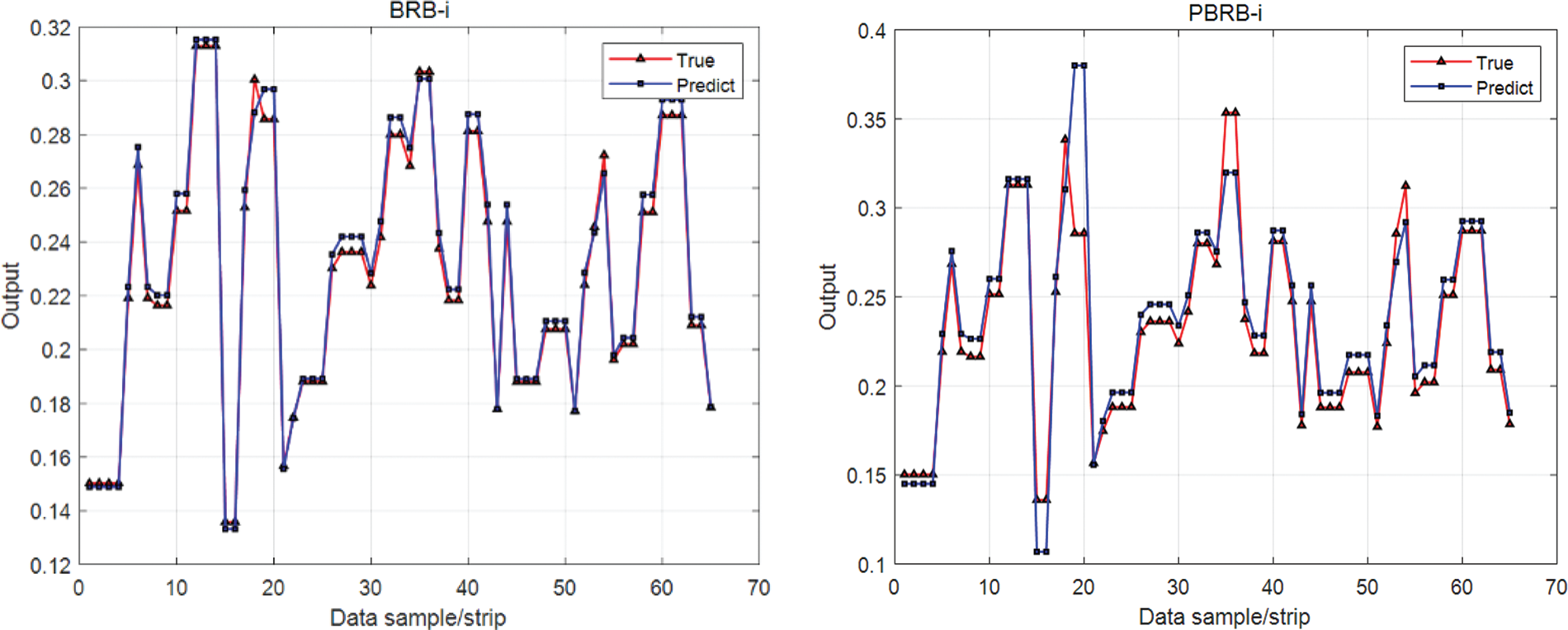
Figure 5: Comparison of the output results of the BRB-i and PBRB-i models with the actual values

Figure 6: Comparison diagram of belief distribution of each rule in BRB-i and PBRB-i
As seen from Fig. 5, both the true and predicted data fits of the interpretable BRB based on both WOA and P-CMA-ES optimization algorithms are better. This indicates that the experimental results of both models possess high accuracy. As shown in Fig. 6, the output belief distributions of the explainable BRB models based on the WOA and P-CMA-ES optimization algorithms follow the same trend as the initial belief distribution set by the expert knowledge, which indicates that the output belief distributions of the models do not violate the initial belief distributions set by the experts, reflecting the excellent interpretability of the models. A comprehensive analysis of Figs. 5 and 6 shows that the proposed BRB-i model has high experimental accuracy and interpretability. The output of the optimized rule weight and belief distribution is shown in Table 7.

According to the above experimental results, the output results of the BRB-i model are close to the fundamental values in precision. Moreover, the optimized belief distribution fits well with the initial belief distribution, which indicates the validity and accuracy of the constructed BRB-i model. It can be seen that the optimization model has a good effect on parameter adjustment and is interpretable.
5.3 Other Comparative Experiments
(1) Results of Various Methods
Several control experiments were also set up in this experiment. The methods used were BRB using the original WOA (WOA-BRB) [17], BRB using P-CMA-ES (PCMAES-BRB), radial basis function (RBF) neural network [27], and extreme learning machine (ELM) [28]. The BRB-i model, WOA-BRB model, and PCMAES-BRB model are all based on expert systems, while RBF and ELM are based on data-driven methods. In terms of experimental accuracy, the comparison between the actual value of PCMAES-BRB and WOA-BRB and the model output value is shown in Fig. 7.

Figure 7: Comparison curve between the output results of the PCMAES-BRB and WOA-BRB model and the actual value
In addition, in terms of interpretability, the comparison between the initial belief distribution set by the expert knowledge and the belief distribution after adjustment and correction of the established model is shown in Fig. 8.

Figure 8: Comparison diagram of the belief distribution of each rule in WOA-BRB and PCMAES-BRB
As seen in Fig.7, the prediction results of WOA-BRB and PCMAES-BRB models that do not possess interpretable constraints also possess high accuracy. BRB-i and PBRB-i also possess high experimental accuracy. This indicates that the BRB model, with the addition of interpretable constraints, has little effect on the experimental accuracy and still maintains high accuracy. However, as can be seen from Fig. 8, the output belief distributions of multiple rules of PCMAES-BRB and WOA-BRB violate the trend of the initial belief distribution set by expert knowledge, which deviates from the interpretability. The comprehensive analysis shows that WOA-BRB and PCMAES-BRB, without adding interpretable constraints, have high experimental accuracy but violate interpretability [29].
The RBF and ELM models based on the data-driven method are not interpretable. The fitting diagram of experimental results in terms of accuracy is shown in Fig. 9.

Figure 9: Comparison curve between the output results of RBF and ELM model and the actual value
(2) Experimental Results of Each Method under Different Proportions of Training Samples
Due to the particular spaceflight background of liquid launch vehicles, their data sets are difficult to collect and there needs to be more methods for their safety assessment. ELM, RBF, and BRB, as standard liquid rocket safety assessment methods, are used to compare with the model proposed in this paper [30]. This experiment does not modify the essence of the WOA and P-CMA-ES algorithms. Nevertheless, it only adds interpretable constraints to this optimization algorithm to ensure the interpretability of the model. When the proportion of model training samples is different, the accuracy of each method is shown in Table 8. After improving the WOA algorithm, the optimization algorithm is used as the proposed BRB-i model’s optimization model. The experiments compare not only the BRB model based on the conventional P-CMA-ES and WOA optimization algorithm but also the models PBRB-i and BRB-i with the addition of interpretable constraints to the conventional P-CMA-ES and WOA optimization algorithms. As shown in Table 8, BRB-i and PBRB-i represent interpretable BRB based on WOA and PCMAES optimization algorithms, respectively. WOA-BRB and PCMAES-BRB distributions represent conventional BRBs based on WOA and PCMAES optimization algorithms. RBF and ELM are models based on data-driven approaches.

As seen from Table 8, the rule-based BRB-i, PBRB-i, WOA-BRB, and PCMAES-BRB models have a smaller range of accuracy fluctuation compared to the data-driven model-based RBF and ELM for different proportions of training samples. This proves that the BRB-based models have high accuracy even with small samples. From Table 8, it can be found that the difference between the accuracy of BRB-i and PBRB-i with interpretability and WOA-BRB and PCMAES-BRB models without interpretability is not significant, which indicates that adding interpretability constraints to the WOA and P-CMA-ES algorithms The addition of interpretable constraints to the WOA andP-CMA-ES algorithms did not affect the accuracy of the models.
(3) Complexity Comparison of Different BRBs
The complexity pairs of the different BRBs are shown in Table 9.

WOA denotes the whale optimization algorithm. R denotes the number of rules. PCMAES denotes the PCMAES optimization algorithm. The four different kinds of BRB have same complexity of space, which is mainly determined by the number of belief rules. The main difference in the time complexity between the four BRB kinds is reflected in their different optimization algorithms. For a BRB model, suppose there are N classes, M attributes and the number of reference values of each attribute is
The number is for the belief degrees of the consequence in all belief rules
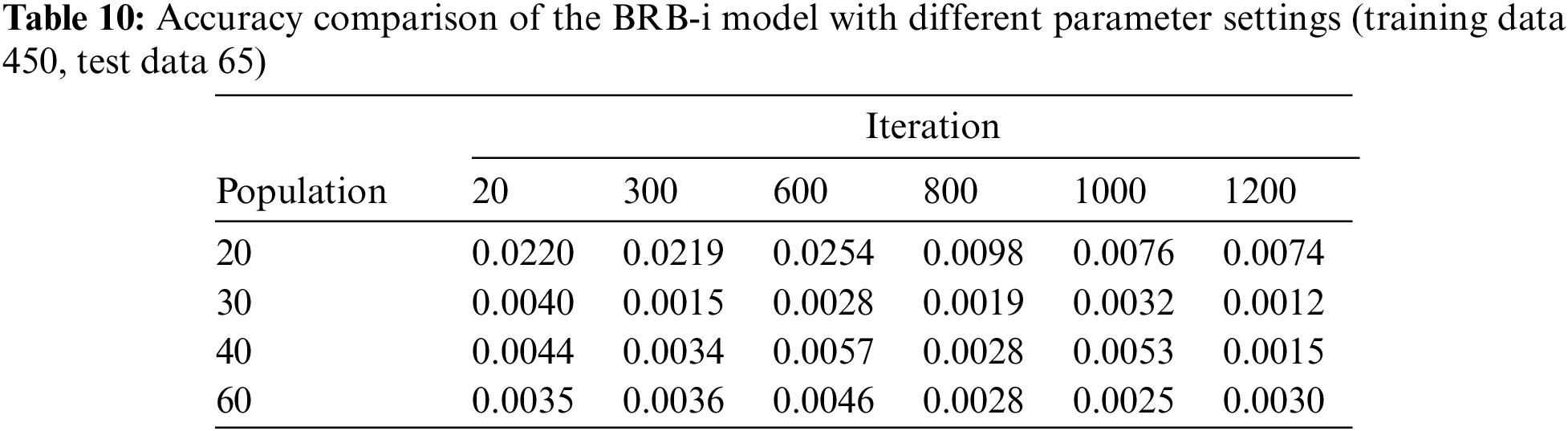
(4) Table of Experimental Results of BRB-i Model with Different Parameter Settings
Under different initial parameter settings of the optimization model, the accuracy comparison of the proposed model is shown in Table 10. Generally, before reaching a specific value, the number of iterations and population size is positively correlated with the optimization ability of the model, but the optimization time will also increase. As seen from Table 10, when the number of iterations reaches 800, and the population number reaches 30, the model’s accuracy will not change significantly.
As a typical complex device, the safety status of the liquid launch vehicle is closely related to the status of several components, and BRB-i, as a general safety assessment model, is also applicable to the safety assessment of the overall liquid launch vehicle system. However, the difference in the actual assessment process is mainly reflected in the following two aspects. First, the structure of the model is more complex. Before the BRB-i model is used for the safety assessment of the overall liquid launch vehicle system, different components and index levels must be distinguished. On this basis, the overall initial BRB model is constructed based on expert knowledge and actual equipment management experience. Second, the model has more parameters to be optimized. As the number of evaluation indicators in the overall liquid launch vehicle system increases, the number of parameters to be optimized in the BRB-i model will also increase, and maintaining the interpretability of the model within the range of more indicators is also a key consideration in the subsequent study [31].
5.4 Analysis and Summary of the Experiment
As shown in Table 8, the MSE values of the proposed BRB-i model are 3.8000e-03, 1.3000e-03, 2.1000e-03, and 1.8936e-04 with a maximum difference of 102 orders of magnitude at the training sample proportions of 25%, 45%, 65%, and 85%, respectively. However, the MSE values of the data-driven ELM-based model, for example, are 1.6010e-01, 3.1200e-02, 2.6000e-03, and 8.6609e-04, with a maximum difference of 104 orders of magnitude. As can be seen from Figs. 5, 7, 9 and Table 8, BRB-i, PBRB-i, WOA-BRB and PCMAES-BRB methods based on expert system have similar results accuracy under the condition of different training sample sizes. In contrast, the accuracy of RBF and ELM based on the data-driven approach shows exponential variations. This proves that BRB has good performance when dealing with small sample data. The model accuracy of data-driven RBF and ELM fluctuates relatively wildly when the training sample size changes, which proves that the experimental accuracy of data-driven methods depends on data samples. Under the same proportion of training and test samples, the accuracy of BRB-i and the data-driven model are similar. Nevertheless,BRB-i is interpretable, while the internal structure of the data-driven RBF and ELM is not visible. This is because brb-i has the following characteristics: (1) BRB can maximize expert knowledge based on long-term practice, while data-driven RBF and ELM do not have this ability. (2) BRB-i has a transparent inference engine, and the inference process itself is built-in interpretability. However, RBF and ELM cannot explain the internal principle. (3) BRB-i has a WOA optimization algorithm with interpretable constraints, while the data-driven model cannot define unreasonable parameters [32].
Additionally, as shown in Table 8, the two optimization algorithms equipped with interpretable constraints did not reduce the accuracy of the experimental results compared with the original. Figs. 6 and 8 show that the belief distribution of the model with interpretable constraints tends to be more reasonable. The BRB-i model has good interpretability, while WOA-BRB and PCMAES-BRB do not. This shows that the proposed BRB-i model has good interpretability. This is because BRB-i has the following characteristics: (1) BRB-i spreads the points more rationally.The initial scattering method of BRB-i is expert-centered, while WOA-BRB and PCMAES-BRB are global random scattering. (2) BRB-i restricts the range of beliefs to be taken, making it more reasonable. However, WOA-BRB and PCMAES-BRB do not have this restriction. (3) BRB-i can solve the problem that the distribution of optimized beliefs reasonably needs to be revised. However, WOA-BRB and PCMAES-BRB also do not have such a constraint.
For the complex modeling problem of the liquid launch vehicle structural safety assessment model, the modeling method BRB-i based on an interpretable belief rule base is proposed. Aiming at the problem of interpretability, a whale optimization algorithm with interpretable constraints was proposed based on the belief rule base (BRB), and a safety evaluation model of liquid launch vehicle body structure with an interpretable belief rule base was constructed. The model uses BRB’s expert knowledge base for initial modeling, ER for reasoning, and the WOA algorithm with interpretable constraints for optimization.
The BRB-i model has better performance in both accuracy and model interpretability dimensions. (1) The BRB-i model sets interpretability constraints in the optimization process, which ensures the interpretability of the model optimization. (2) The inference process constructed based on the belief rule base can trace the cause of failure, and the inference process is interpretable. (3) The BRB-i model can still guarantee the model’s accuracy in the small sample case.
In future research, the following research directions can be considered. (1) How to embed the fuzzy fault tree mechanism into the expert knowledge base to make the modeling process explainable. (2) How can the combinatorial rule explosion problem that may be triggered by the BRB-i model be solved when the number of reference points and premise attributes grows exponentially.
Acknowledgement: Mr. He Wei for his guidance and revision and Mr. Han Peng for answering many questions for me.
Funding Statement: This work was supported in part by the Natural Science Foundation of China under Grant 62203461 and Grant 62203365, in part by the Postdoctoral Science Foundation of China under Grant No. 2020M683736, in part by the Teaching Reform Project of Higher Education in Heilongjiang Province under Grant Nos. SJGY20210456 and SJGY20210457, in part by the Natural Science Foundation of Heilongjiang Province of China under Grant No. LH2021F038, and in part by the Graduate Academic Innovation Project of Harbin Normal University under Grant Nos. HSDSSCX2022-17, HSDSSCX2022-18 and HSDSSCX2022-19.
Author Contributions: G.X. and X.C. contributed equally to this work. Conceptualization, G.X., and X.C. ; methodology, X.C. ; software, X.C. ; validation, G.X., W.H., and P.H. ; formal analysis, X.C. ; investigation, G.X. ; resources, G.X. ; data curation, G.X. ; writing—original draft preparation, X.C. ; writing—review and editing, W.H. ; visualization, G.X. ; supervision, P.H. ; project administration, X.C. ; funding acquisition, W.H. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. L. Xu, S. Zhao, N. Li, Q. Gao, T. Wang et al., “Application of QGA-BP for fault detection of liquid launch vehicle engines,” IEEE Transactions on Aerospace and Electronic Systems, vol. 55, no. 5, pp. 2464–2472, 2019. [Google Scholar]
2. M. H. Shaikh and K. Barbe, “Study of random forest to identify Wiener-Hammerstein system,” IEEE Transactions on Instrumentation and Measurement, vol. 70, pp. 1–12, 2021. [Google Scholar]
3. N. Karmitsa, S. Taheri, A. Bagirov and P. Makinen, “Missing value imputation via clusterwise linear regression,” IEEE Transactions on Knowledge and Data Engineering, vol. 34, no. 4, pp. 1889–1901, 2022. [Google Scholar]
4. Y. Zheng, H. Duan, C. Wang, R. C. Wang and S. Nepal, “Securely and efficiently outsourcing decision tree inference,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 3, pp. 1841–1855, 2022. [Google Scholar]
5. Z. C. Feng, W. He, Z. J. Zhou, X. J. Ban, C. H. Hu et al., “A new safety assessment method based on belief rule base with attribute reliability,” IEEE/CAA Journal of Automatica Sinica, vol. 8, no. 11, pp. 1774–1785, 2021. [Google Scholar]
6. Q. Tang, M. Xie, K. Yang, Y. S. Luo, D. D. Zhou et al., “A decision function based smart charging and discharging strategy for electric vehicle in smart grid,” Mobile Networks and Applications, vol. 24, no. 5, pp. 1722–1731, 2019. [Google Scholar]
7. Z. Xu, W. Liang, K. C. Li, J. Xu and H. Jin, “A blockchain-based roadside unit-assisted authentication and key agreement protocol for internet of vehicles,” Journal of Parallel and Distributed Computing, vol. 149, no. 6, pp. 29–39, 2020. [Google Scholar]
8. K. Lee, J. Cha, S. Ko, S. Y. Park and E. Jung, “Fault detection and diagnosis algorithms for an open-cycle liquid propellant rocket engine using the Kalman filter and fault factor methods,” Acta Astronautica, vol. 150, no. 6, pp. 15–27, 2018. [Google Scholar]
9. S. Y. Park and J. Ahn, “Deep neural network approach for fault detection and diagnosis during startup transient of liquid-propellant rocket engine,” Acta Astronautica, vol. 177, pp. 714–730, 2020. https://doi.org/10.1016/j.actaastro.2020.08.019 [Google Scholar] [CrossRef]
10. H. Yu and T. Wang, “A method for real-time fault detection of liquid launch vehicle engine based on adaptive genetic algorithm optimizing back propagation neural network,” Sensors, vol. 21, no. 15, pp. 5026, 2021. [Google Scholar] [PubMed]
11. D. Hong, T. Gu and J. Baik, “A UML model based white box reliability prediction to identify unreliable components,” in 2011 Fifth Int. Conf. on Secure Software Integration and Reliability Improvement—Companion, Jeju, Korea (Southpp. 152–159, 2011. https://doi.org/10.1109/SSIRI-C.2011.30 [Google Scholar] [CrossRef]
12. Y. C. Zhang, Y. Xu, S. Q. Bu, Z. Y. Dong and R. Zhang, “Online power system dynamic security assessment with incomplete PMU measurements: A robust white-box model,” IET Generation, Transmission & Distribution, vol. 13, no. 5, pp. 662–668, 2019. https://doi.org/10.1049/iet-gtd.2018.6241 [Google Scholar] [CrossRef]
13. V. Osipov, C. Muratov, H. Hafiychuk, E. Ponizovskaya-Devine, V. Smelyanskiy et al., “Explosion hazard from a propellant-tank breach in liquid hydrogen-oxygen rockets,” Journal of Spacecraft & Rockets, vol. 50, no. 4, pp. 860–871, 2015. [Google Scholar]
14. Z. M. Zhu, X. Gao, X. J. Wang, Q. L. Han and H. Cui, “Safety assessment of solid rocket motor waterjet clearing system based on grey analytic hierarchy process,” 2nd Int. Conf. on Mechanical Engineering, Materials Science and Civil Engineering (ICMEMSCE), vol. 470, pp. 763–766, 2013. [Google Scholar]
15. Y. W. Chen, J. B. Yang, D. L. Xu and S. L. Yang, “On the inference and approximation properties of belief rule-based systems,” Information Sciences, vol. 234, no. 4, pp. 121–135, 2013. [Google Scholar]
16. Y. Cao, Z. J. Zhou, C. H. Hu, S. W. Tang and J. Wang, “A new approximate belief rule base expert system for complex system modelling,” Decision Support Systems, vol. 150, pp. 113558, 2021. [Google Scholar]
17. X. Chen, L. Cheng, C. Liu, Q. Z. Liu, J. W. Liu et al., “A WOA-based optimization approach for task scheduling in cloud computing systems,” IEEE Systems Journal, vol. 14, no. 3, pp. 3117–3128, 2020. [Google Scholar]
18. Y. Cao, Z. J. Zhou, C. H. Hu, W. He and S. W. Tang, “On the interpretability of belief rule-based expert systems,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 11, pp. 3489–3503, 2021. [Google Scholar]
19. J. B. Yang, “Rule and utility based evidential reasoning approach for multi-attribute decision analysis under uncertainties,” European Journal of Operational Research, vol. 131, no. 1, pp. 31–61, 2001. [Google Scholar]
20. Z. C. Feng, Z. J. Zhou, C. H. Hu, L. L. Chang, G. Y. Hu et al., “A new belief rule base model with attribute reliability,” IEEE Transactions on Fuzzy Systems, vol. 27, no. 5, pp. 903–916, 2019. [Google Scholar]
21. X. Y. Cheng, P. Han, W. He, P. Zhang, X. X. Han et al., “A new flywheel health status assessment model based on explicable belief rule base,” Acta Aeronautica et Astronautica Sinica, pp. 1–13, 2022. https://doi.org/10.7527/S1000-6893.2022.27496 [Google Scholar] [CrossRef]
22. Y. You, J. Sun, Y. Guo, Y. J. Tan and J. Jiang, “Interpretability and accuracy trade-off in the modeling of belief rule-based systems,” Knowledge-Based Systems, vol. 236, no. 2, pp. 107491, 2022. [Google Scholar]
23. Z. T. Zhou, X. Y. Liang, C. F. Zhao, G. G. Le and Y. F. Ding, “Investigations of base thermal environment on four-nozzle liquid launch vehicle at high altitude,” Journal of Spacecraft and Rockets, vol. 57, no. 1, pp. 49–57, 2020. [Google Scholar]
24. S. Yue, B. Titurus, H. Nie and M. Zhang, “Liquid spring damper for vertical landing reusable launch vehicle under impact conditions,” Mechanical Systems and Signal Processing, vol. 121, no. 1, pp. 579–599, 2019. [Google Scholar]
25. C. H. Hu, Z. C. Feng, Z. J. Zhou, G. Y. Hu, W. He et al., “A safety assessment method for a liquid launch rocket based on the belief rule base with environmental disturbance,” Scientia Sinica Informationis, vol. 50, no. 10, pp. 1674–7267, 2020. [Google Scholar]
26. L. Qu, R. Zheng and Y. Shi, “BSO-CMA-ES: Brain storm optimization based covariance matrix adaptation evolution strategy for multimodal optimization,” in Int. Conf. on Data Mining and Big Data, Singapore, Springer, pp. 167–174, 2021. [Google Scholar]
27. M. Barnard, F. M. Lagnf, A. S. Mahmoud and M. Zohdy, “Speech enhancement and recognition using Kalman filter modified via radial basis function,” International Journal of Computer and Information Technology, vol. 9, no. 2, pp. 2279–0764, 2020. [Google Scholar]
28. H. M. Zhao, H. D. Liu, J. J. Xu and W. Deng, “Performance prediction using high-order differential mathematical morphology gradient spectrum entropy and extreme learning machine,” IEEE Transactions on Instrumentation and Measurement, vol. 69, no. 7, pp. 4165–4172, 2019. [Google Scholar]
29. S. M. B. Haider and D. Lee, “A review on BRB and SC-BRB members in building structures,” Structural Engineering and Mechanics, vol. 80, no. 5, pp. 609–623, 2021. [Google Scholar]
30. C. H. Hu, Z. C. Feng, Z. J. Zhou, G. Y. Hu and W. He, “A safety assessment method for a liquid launch rocket based on the belief rule base with environmental disturbance (in Chinese),” Scientia Sinica Informationis, vol. 50, no. 10, pp. 1559–1573, 2020. https://doi.org/10.1360/SSI-2019-0148 [Google Scholar] [CrossRef]
31. X. Zhou, T. Sun, B. Sun, N. Ma and J. Ou, “Vibration-reduction strategy for high-rise braced frame using viscoelastic-yielding compounded BRB,” Buildings, vol. 12, no. 8, pp. 1159, 2022. [Google Scholar]
32. L. H. Gilpin, D. Bau, B. Z. Yuan, A. Bajwa, M. Specter et al., “Explaining explanations: An overview of interpretability of machine learning,” in 2018 IEEE 5th Int. Conf. on Data Science and Advanced Analytics (DSAA), Turin, Italy, pp. 80–89, 2018. https://doi.org/10.1109/DSAA.2018.00018 [Google Scholar] [CrossRef]
Cite This Article
This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
