2 3.GLMの基礎
- 1. 一般化線形モデル基礎 1
- 2. 2 一般化線形モデルをマスターしよう 予測と確率分布 尤度と最尤法 一般化線形モデル基礎 Devianceと尤度比検定 一般化線形モデル色々 是非!! ゼロ切断・過剰モデル、 一般化線形混合モデル
- 3. 3 GLM やります 一般化線形モデル [Generalized Linear Model]
- 4. 4 GLMとは? 昨日やった正規線形モデルのパワーアップVer 正規分布以外の確率分布も使える統計モデル • ブレーキを踏んでもバックしない • ゾンビ猫が存在しない 一般化線形モデル(GLM)
- 6. 6 今回の内容 一般化線形モデル(GLM)の雰囲気をつかもう 1.GLMの構成要素を知る • 線形予測子 • リンク関数 • 誤差構造 2.GLMの一種、ポアソン回帰を実装する
- 8. 8 線形予測子 方程式 𝑌 = 𝑎𝑋 + 𝑏 例) ビールの売り上げ=a×気温+b
- 9. 9 リンク関数 例えばデータが0以上しかとらないならば、 予測の方程式も0以上になっていてほしい 𝑌 = 𝑒 𝑎𝑋+𝑏 log 𝑌 = 𝑎𝑋 + 𝑏 リンク関数=ログ 方程式を変換する関数のこと 線形予測子 応答変数
- 10. 10 リンク関数いろいろ 1 𝑌 = 𝑎𝑋 + 𝑏 log 𝑌 = 𝑎𝑋 + 𝑏 log 𝑝 1 − 𝑝 = 𝑎𝑋 + 𝑏 ログ (log) 逆関数 (inverse) ロジット (logit)
- 11. 11 リンク関数いろいろ log 𝑌 = 𝑎𝑋 + 𝑏 ログ (log) 𝑌 = 𝑒 𝑎𝑋+𝑏 𝑌 = 𝑒 𝑎𝑋 × 𝑒 𝑏 掛け算になっている! Xが1増えると、Yは𝒆 𝒂 倍になる
- 12. 12 リンク関数いろいろ log 𝑌 = 𝑎𝑋 + 𝑏 リンク関数:ログ (log) 係数の解釈が変わるので注意! Xが1増えると、Yは𝒆 𝒂 倍になる 𝑌 = 𝑎𝑋 + 𝑏 Xが1増えると、Yはa増える リンク関数:なし (identity)
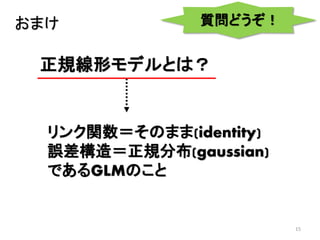
- 14. 14 まとめ 1.線形予測子 2.リンク関数 3.誤差構造 𝑌 = 𝑎𝑋 + 𝑏のような方程式 log 𝑌 = 𝑎𝑋 + 𝑏のような変換 正規・ポアソン分布のような確率分布
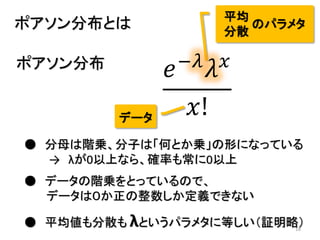
- 18. 18 ポアソン分布とは ポアソン分布 平均 分散 のパラメタ データ ● 分母は階乗、分子は「何とか乗」の形になっている → λが0以上なら、確率も常に0以上 ● データの階乗をとっているので、 データは0か正の整数しか定義できない ● 平均値も分散も λというパラメタに等しい(証明略) 𝑒−𝜆 𝜆 𝑥 𝑥!
- 21. 21 確率 ○○かつ○○になる確率 → 掛け算!! 偶数になる確率: 1/2 3の倍数になる確率: 1/3 偶数かつ3の倍数になる確率: 1/2×1/3=1/6
- 22. 22 尤度とは 1 3 × 1 − 1 3 = 1 3 × 2 3 = 2 9 表の確率 裏の確率 今回のデータが生じる確率 パラメタを指定したときに、 今手持ちのデータが再現できる確率 尤度!! 表になる確率は1/3だ!!
- 23. 23 最尤法とは 尤度が最大になるようにパラメタを決めること パラメタは1/3だ!! 1 3 × 1 − 1 3 = 1 3 × 2 3 = 2 9 パラメタは1/2だ!! 1 2 × 1 − 1 2 = 1 2 × 1 2 = 1 4 こっちの方がデカい! こっちを採用!!
- 24. 24 ポアソン回帰 データが4セットあります(サンプルサイズ4) Y : 7, 9, 8, 11 Yはポアソン分布に従います。 平均はλで一定とします。 λを最尤推定しなさい
- 25. 25 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説1 パラメタλは5だ! データ 「7」 が出る確率は? 𝑒−5 57 7! ≒ 0.10 λ=5 y=7 Y : 7, 9, 8, 11
- 26. 26 ポアソン回帰 Y : 7, 9, 8, 11 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説1 パラメタλは5だ! データ 「9」 が出る確率は? 𝑒−5 59 9! ≒ 0.04 λ=5 y=9
- 27. 27 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説1 パラメタλは5だ! データ 「8」 が出る確率は? 𝑒−5 58 8! ≒ 0.07 λ=5 y=8 Y : 7, 9, 8, 11
- 28. 28 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説1 パラメタλは5だ! データ 「11」 が出る確率は? 𝑒−5 511 11! ≒ 0.01 λ=5 y=11 Y : 7, 9, 8, 11
- 29. 29 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説1 パラメタλは5だ! Y : 7, 9, 8, 11 尤度 ≒ 0.10 × 0.04 × 0.07 × 0.01 ≒ 0.0000028
- 30. 30 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦!Y : 7, 9, 8, 11 尤度 ≒ 0.12 × 0.13 × 0.13 × 0.10 ≒ 0.0002028 仮説2 パラメタλは9だ!
- 31. 31 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦!Y : 7, 9, 8, 11 尤度 ≒ 0.12 × 0.13 × 0.13 × 0.10 ≒ 0.0002028 仮説2 パラメタλは9だ! 仮説1 パラメタλは5だ! 尤度 ≒ 0.10 × 0.04 × 0.07 × 0.01 ≒ 0.0000028 こっちの方がデカい! こっちを採用!!
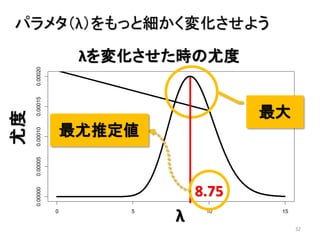
- 32. 32 パラメタ(λ)をもっと細かく変化させよう 0 5 10 15 0.000000.000050.000100.000150.00020 λ 確率 λを変化させた時の尤度 λ 最大 8.75 最尤推定値
- 33. 33 実演 質問どうぞ!
- 34. 34 ポアソン回帰 データが4セットあります(サンプルサイズ4) Y : 5, 7, 10, 15 Yはポアソン分布に従います。 平均はXによって変化するとします。 log(λ) = aX + b a、bを最尤推定しなさい X : 1, 2, 3, 4
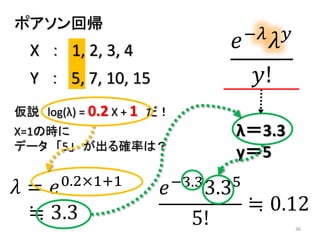
- 35. 35 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説 log(λ) = 0.2 X + 1 だ! X=1の時に データ 「5」 が出る確率は? 𝑒−3.33.35 5! ≒ 0.12 λ=3.3 y=5 Y : 5, 7, 10, 15 X : 1, 2, 3, 4 𝜆 = 𝑒0.2×1+1 ≒ 3.3
- 36. 36 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! X=1の時に データ 「5」 が出る確率は? 𝑒−3.33.35 5! ≒ 0.12 λ=3.3 y=5 Y : 5, 7, 10, 15 X : 1, 2, 3, 4 𝜆 = 𝑒0.2×1+1 ≒ 3.3 仮説 log(λ) = 0.2 X + 1 だ!
- 37. 37 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説 log(λ) = 0.2 X + 1 だ! X=2の時に データ 「7」 が出る確率は? 𝑒−4.14.17 7! ≒ 0.06 λ=4.1 y=7 Y : 5, 7, 10, 15 X : 1, 2, 3, 4 𝜆 = 𝑒0.2×2+1 ≒ 4.1
- 38. 38 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説 log(λ) = 0.2 X + 1 だ! X=3の時に データ 「10」 が出る確率は? 𝑒−5.05.010 10! ≒ 0.02 λ=4.1 y=10 Y : 5, 7, 10, 15 X : 1, 2, 3, 4 𝜆 = 𝑒0.2×3+1 ≒ 5.0
- 39. 39 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 仮説 log(λ) = 0.2 X + 1 だ! X=4の時に データ 「15」 が出る確率は? 𝑒−6.06.015 15! ≒ 0.001 λ=6.0 y=15 Y : 5, 7, 10, 15 X : 1, 2, 3, 4 𝜆 = 𝑒0.2×4+1 ≒ 6.0
- 40. 40 ポアソン回帰 𝑒−𝜆 𝜆 𝑦 𝑦! 尤度 ≒ 0.12 × 0.06 × 0.02 × 0.001 ≒ 0.000000144 Y : 5, 7, 10, 15 X : 1, 2, 3, 4 仮説 log(λ) = 0.2 X + 1 だ!
- 41. 41 実演 質問どうぞ!
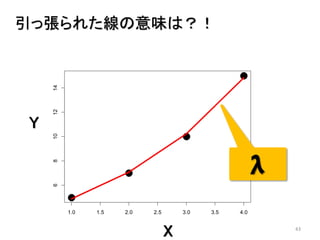
- 43. 43 1.0 1.5 2.0 2.5 3.0 3.5 4.0 68101214 x y 引っ張られた線の意味は?! λ Y X
- 44. 44 1.0 1.5 2.0 2.5 3.0 3.5 4.0 68101214 x y 引っ張られた線の意味は?! x=1の時 λ=4.88 𝑒−𝜆 𝜆 𝑦 𝑦! 𝑒−4.88 4.88 𝑦 𝑦! x=1の時の Yの確率分布 Y X
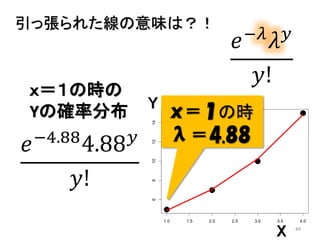
- 45. 450 5 10 15 0.000.050.100.15 dpois(y,best.lambda[1]) 引っ張られた線の意味は?! λ=4.88 の確率分布 x=1の時… y=0の確率:0.0076 y=1の確率:0.0371 y=5の確率:0.1752 y=10の確率:0.0160 Y
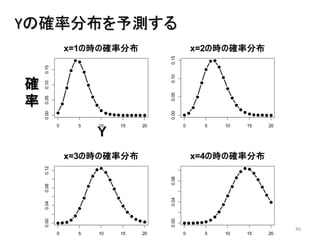
- 46. 46 Yの確率分布を予測する 0 5 10 15 20 0.000.050.100.15 x=1の時の確率分布 0 5 10 15 20 0.000.050.100.15 x=2の時の確率分布 0 5 10 15 20 0.000.040.080.12 x=3の時の確率分布 0 5 10 15 20 0.000.040.08 x=4の時の確率分布 Y 確 率
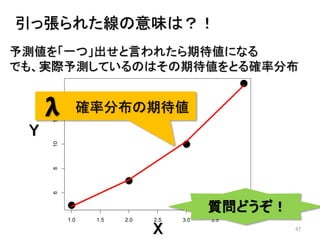
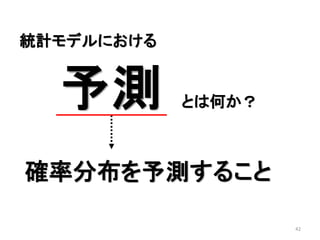
- 47. 47 1.0 1.5 2.0 2.5 3.0 3.5 4.0 68101214 x y 引っ張られた線の意味は?! 質問どうぞ! Y X 確率分布の期待値λ 予測値を「一つ」出せと言われたら期待値になる でも、実際予測しているのはその期待値をとる確率分布

![3
GLM やります
一般化線形モデル
[Generalized Linear Model]](https://image.slidesharecdn.com/23-130826212530-phpapp02/85/2-3-GLM-3-320.jpg)




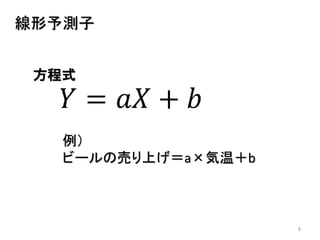





























![450 5 10 15
0.000.050.100.15
dpois(y,best.lambda[1])
引っ張られた線の意味は?!
λ=4.88
の確率分布
x=1の時…
y=0の確率:0.0076
y=1の確率:0.0371
y=5の確率:0.1752
y=10の確率:0.0160
Y](https://image.slidesharecdn.com/23-130826212530-phpapp02/85/2-3-GLM-45-320.jpg)