Functional Programming Patterns (BuildStuff '14)
- 1. Functional Design Patterns @ScottWlaschin fsharpforfunandprofit.com
- 2. Functional Design Patterns @ScottWlaschin fsharpforfunandprofit.com X
- 3. Functional Design Patterns @ScottWlaschin fsharpforfunandprofit.com
- 7. Functional patterns •Apomorphisms •Dynamorphisms •Chronomorphisms •Zygohistomorphic prepromorphisms
- 8. Functional patterns •Core Principles of FP design –Functions, types, composition •Functions as parameters –Abstraction, Dependency injection –Partial application, Continuations, Folds, •Chaining functions –Error handling, Async –Monads •Dealing with wrapped data –Lifting, Functors –Validation with Applicatives •Aggregating data and operations –Monoids
- 9. This talk A whirlwind tour of many sights Don't worry if you don't understand everything
- 10. Functional programming is scary
- 11. Functional programming is scary
- 12. Object oriented programming is scary
- 13. •Single Responsibility Principle •Open/Closed principle •Dependency Inversion Principle •Interface Segregation Principle •Factory pattern •Strategy pattern •Decorator pattern •Visitor pattern •Functions •Functions •Functions, also •Functions •Yes, functions •Oh my, functions again! •Functions •Functions OO pattern/principle FP pattern/principle Seriously, FP patterns are different
- 14. A short and mostly wrong history of programming paradigms
- 15. •What we envisioned: –Smalltalk •What we got: –C++ –Object oriented Cobol –PHP –Java “Worse is better” Object-Oriented programming
- 16. •What we envisioned: –Haskell, OCaml, F#, etc •What we got: –?? Functional programming Please don’t let this happen to FP!
- 17. CORE PRINCIPLES OF FP DESIGN Important to understand!
- 18. Core principles of FP design Steal from mathematics Types are not classes Functions are things Composition everywhere Function
- 19. Core principle: Steal from mathematics “Programming is one of the most difficult branches of applied mathematics” - E. W. Dijkstra
- 20. Why mathematics Dijkstra said: •Mathematical assertions tend to be unusually precise. •Mathematical assertions tend to be general. They are applicable to a large (often infinite) class of instances. •Mathematics embodies a discipline of reasoning allowing assertions to be made with an unusually high confidence level.
- 21. “Object-oriented programming is an exceptionally bad idea which could only have originated in California.” E. W. Dijkstra
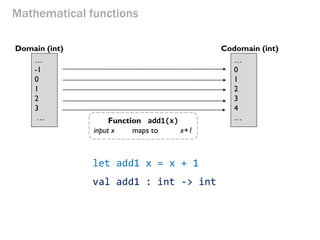
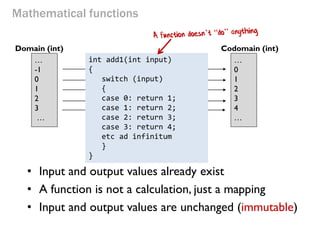
- 22. Mathematical functions Function add1(x) input x maps to x+1 … -1 0 1 2 3 … Domain (int) Codomain (int) … 0 1 2 3 4 … let add1 x = x + 1 val add1 : int -> int
- 23. Function add1(x) input x maps to x+1 … -1 0 1 2 3 … Domain (int) Codomain (int) … 0 1 2 3 4 … Mathematical functions int add1(int input) { switch (input) { case 0: return 1; case 1: return 2; case 2: return 3; case 3: return 4; etc ad infinitum } } •Input and output values already exist •A function is not a calculation, just a mapping •Input and output values are unchanged (immutable)
- 24. Mathematical functions •A (mathematical) function always gives the same output value for a given input value •A (mathematical) function has no side effects Function add1(x) input x maps to x+1 … -1 0 1 2 3 … Domain (int) Codomain (int) … 0 1 2 3 4 …
- 25. Functions don't have to be about arithmetic Function CustomerName(x) input Customer maps to PersonalName … Cust1 Cust2 Cust3 Cust3 … Customer (domain) Name (codomain) … Alice Bob Sue John Pam… Name CustomerName(Customer input) { switch (input) { case Cust1: return “Alice”; case Cust2: return “Bob”; case Cust3: return “Sue”; etc } }
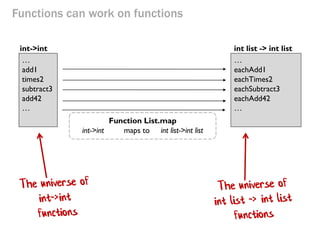
- 26. Functions can work on functions Function List.map int->int maps to int list->int list … add1 times2 subtract3 add42 … int->int int list -> int list … eachAdd1 eachTimes2 eachSubtract3 eachAdd42 …
- 27. Guideline: Strive for purity
- 28. The practical benefits of pure functions customer.SetName(newName); let newCustomer = setCustomerName(aCustomer, newName) Pure functions are easy to reason about var name = customer.GetName(); let name,newCustomer = getCustomerName(aCustomer) Reasoning about code that might not be pure: Reasoning about code that is pure: The customer is being changed.
- 29. The practical benefits of pure functions let x = doSomething() let y = doSomethingElse(x) return y + 1 Pure functions are easy to refactor
- 30. The practical benefits of pure functions Pure functions are easy to refactor let x = doSomething() let y = doSomethingElse(x) return y + 1
- 31. The practical benefits of pure functions Pure functions are easy to refactor let helper() = let x = doSomething() let y = doSomethingElse(x) return y return helper() + 1
- 32. More practical benefits of pure functions •Laziness –only evaluate when I need the output •Cacheable results –same answer every time –"memoization" •No order dependencies –I can evaluate them in any order I like •Parallelizable –"embarrassingly parallel"
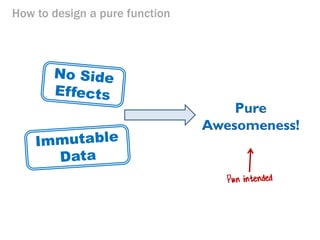
- 33. How to design a pure function Pure Awesomeness!
- 34. How to design a pure function •Haskell –very pure •F#, OCaml, Clojure, Scala –easy to be pure •C#, Java, JavaScript –have to make an effort
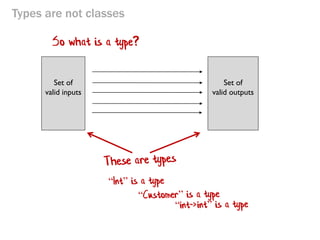
- 35. Core principle: Types are not classes
- 36. X
- 37. Types are not classes Set of valid inputs Set of valid outputs So what is a type?
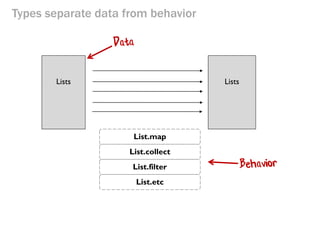
- 38. Types separate data from behavior Lists Lists List.map List.collect List.filter List.etc
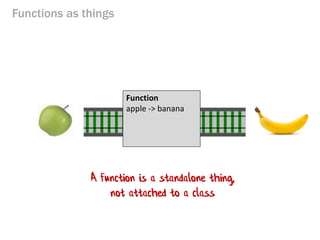
- 39. Core principle: Functions are things Function
- 40. Functions as things The Tunnel of Transformation Function apple -> banana A function is a standalone thing, not attached to a class
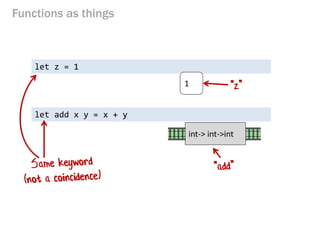
- 41. Functions as things let z = 1 int-> int->int 1 let add x y = x + y
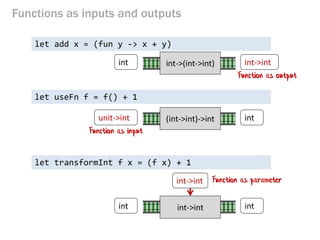
- 42. Functions as inputs and outputs let useFn f = (f 1) + 2 let add x = (fun y -> x + y) int->(int->int) int ->int int int int->int let transformInt f x = (f x) + 1 int->int int int Function as output Function as input Function as parameter (int->int)->int int->int
- 43. Core principle: Composition everywhere
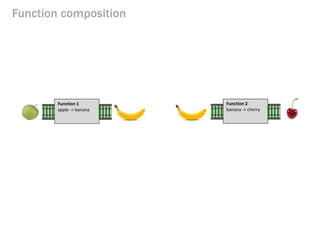
- 44. Function composition Function 1 apple -> banana Function 2 banana -> cherry
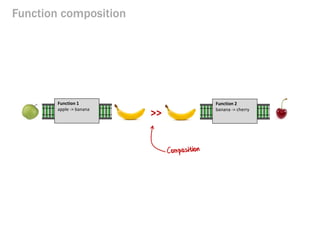
- 45. Function composition >> Function 1 apple -> banana Function 2 banana -> cherry
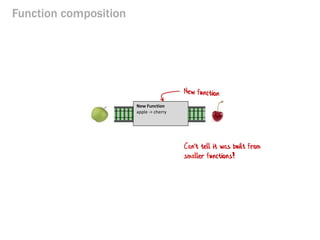
- 46. Function composition New Function apple -> cherry Can't tell it was built from smaller functions!
- 47. Types can be composed too “algebraic types"
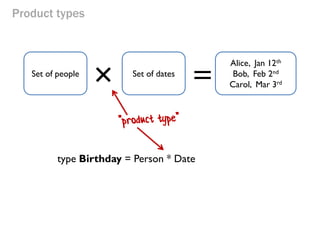
- 48. Product types × = Alice, Jan 12th Bob, Feb 2nd Carol, Mar 3rd Set of people Set of dates type Birthday = Person * Date
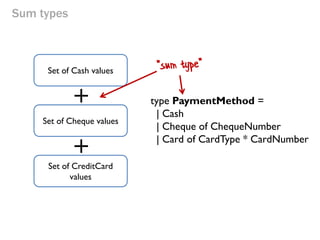
- 49. Sum types Set of Cash values Set of Cheque values Set of CreditCard values + + type PaymentMethod = | Cash | Cheque of ChequeNumber | Card of CardType * CardNumber
- 50. DDD & DOMAIN MODELLING
- 51. Domain modelling pattern: Use types to represent constraints
- 52. Types represent constraints on input and output type Suit = Club | Diamond | Spade | Heart type String50 = // non-null, not more than 50 chars type EmailAddress = // non-null, must contain ‘@’ type StringTransformer = string -> string type GetCustomer = CustomerId -> Customer option Instant mockability
- 53. Domain modelling pattern: Types are cheap
- 54. Types are cheap type Suit = Club | Diamond | Spade | Heart type Rank = Two | Three | Four | Five | Six | Seven | Eight | Nine | Ten | Jack | Queen | King | Ace type Card = Suit * Rank type Hand = Card list Only one line of code to create a type!
- 55. Design principle: Strive for totality
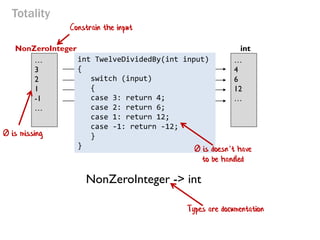
- 56. twelveDividedBy(x) input x maps to 12/x … 3 2 1 0 … Domain (int) Codomain (int) … 4 6 12 … Totality int TwelveDividedBy(int input) { switch (input) { case 3: return 4; case 2: return 6; case 1: return 12; case 0: return ??; } } What happens here?
- 57. twelveDividedBy(x) input x maps to 12/x … 3 2 1 -1 … NonZeroInteger int … 4 6 12 … Totality int TwelveDividedBy(int input) { switch (input) { case 3: return 4; case 2: return 6; case 1: return 12; case -1: return -12; } } Constrain the input 0 is doesn’t have to be handled NonZeroInteger -> int 0 is missing Types are documentation
- 58. twelveDividedBy(x) input x maps to 12/x … 3 2 1 0 -1 … int Option<Int> … Some 4 Some 6 Some 12 None … Totality int TwelveDividedBy(int input) { switch (input) { case 3: return Some 4; case 2: return Some 6; case 1: return Some 12; case 0: return None; } } Extend the output 0 is valid input int -> int option Types are documentation
- 59. Design principle: Use types to indicate errors
- 60. Output types as error codes LoadCustomer: CustomerId -> Customer LoadCustomer: CustomerId -> SuccessOrFailure<Customer> ParseInt: string -> int ParseInt: string -> int option FetchPage: Uri -> String FetchPage: Uri -> SuccessOrFailure<String> No nulls No exceptions Use the signature, Luke!
- 61. Domain modelling principle: “Make illegal states unrepresentable”
- 62. Types can represent business rules type EmailContactInfo = | Unverified of EmailAddress | Verified of VerifiedEmailAddress type ContactInfo = | EmailOnly of EmailContactInfo | AddrOnly of PostalContactInfo | EmailAndAddr of EmailContactInfo * PostalContactInfo
- 63. Domain modelling principle: Use sum-types instead of inheritance
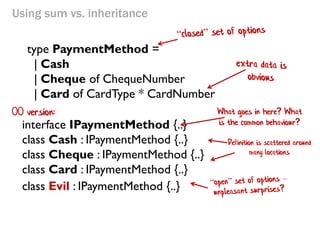
- 64. Using sum vs. inheritance interface IPaymentMethod {..} class Cash : IPaymentMethod {..} class Cheque : IPaymentMethod {..} class Card : IPaymentMethod {..} type PaymentMethod = | Cash | Cheque of ChequeNumber | Card of CardType * CardNumber class Evil : IPaymentMethod {..} Definition is scattered around many locations What goes in here? What is the common behaviour? OO version:
- 65. Domain modelling principle: Use sum-types for state machines
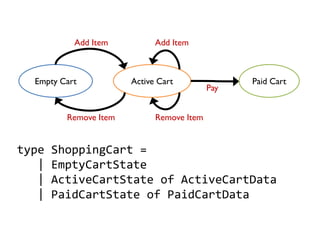
- 66. type ShoppingCart = | EmptyCartState | ActiveCartState of ActiveCartData | PaidCartState of PaidCartData Empty Cart Active Cart Paid Cart Add Item Remove Item Pay Add Item Remove Item
- 67. Domain modelling principle: It’s ok to expose public data
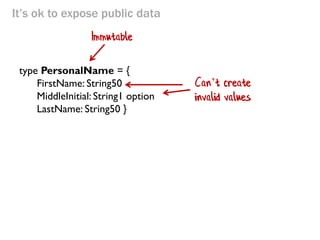
- 68. It’s ok to expose public data type PersonalName = { FirstName: String50 MiddleInitial: String1 option LastName: String50 } Immutable Can’t create invalid values
- 69. Domain modelling principle: Types are executable documentation
- 70. Types are executable documentation type Suit = Club | Diamond | Spade | Heart type Rank = Two | Three | Four | Five | Six | Seven | Eight | Nine | Ten | Jack | Queen | King | Ace type Card = Suit * Rank type Hand = Card list type Deck = Card list type Player = {Name:string; Hand:Hand} type Game = {Deck:Deck; Players: Player list} type Deal = Deck –› (Deck * Card) type PickupCard = (Hand * Card) –› Hand
- 71. Types are executable documentation type CardType = Visa | Mastercard type CardNumber = CardNumber of string type ChequeNumber = ChequeNumber of int type PaymentMethod = | Cash | Cheque of ChequeNumber | Card of CardType * CardNumber
- 72. More on DDD and designing with types at fsharpforfunandprofit.com/ddd Static types only! Sorry Clojure and JS developers
- 74. Design paradigm: Functions all the way down
- 75. “Functions in the small, objects in the large”
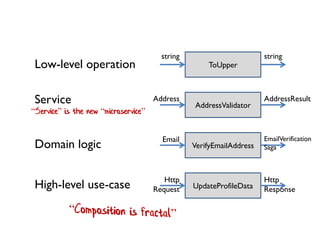
- 76. Low-level operation ToUpper Service Domain logic High-level use-case AddressValidator VerifyEmailAddress UpdateProfileData “Service” is the new “microservice” string string AddressResult EmailVerification Saga Http Response Address Email Http Request
- 77. Design paradigm: Transformation-oriented programming
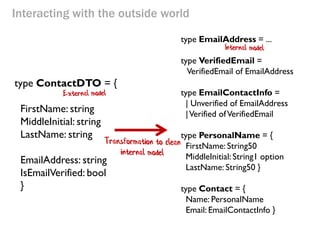
- 78. Interacting with the outside world type ContactDTO = { FirstName: string MiddleInitial: string LastName: string EmailAddress: string IsEmailVerified: bool } type EmailAddress = ... type VerifiedEmail = VerifiedEmail of EmailAddress type EmailContactInfo = | Unverified of EmailAddress | Verified of VerifiedEmail type PersonalName = { FirstName: String50 MiddleInitial: String1 option LastName: String50 } type Contact = { Name: PersonalName Email: EmailContactInfo }
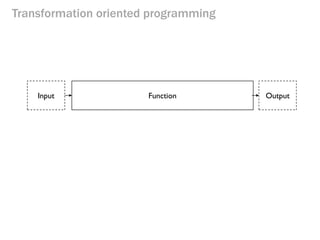
- 79. Transformation oriented programming Input Function Output
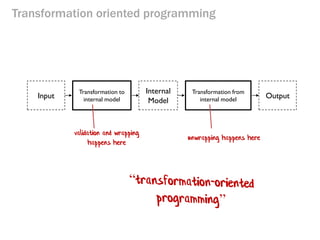
- 80. Transformation oriented programming Input Transformation to internal model Internal Model Output Transformation from internal model validation and wrapping happens here unwrapping happens here
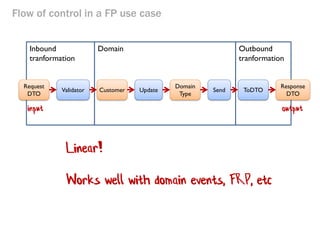
- 81. Outbound tranformation Flow of control in a FP use case Inbound tranformation Customer Domain Validator Update Request DTO Domain Type Send ToDTO Response DTO Works well with domain events, FRP, etc
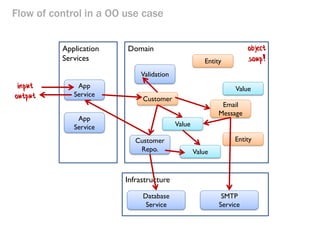
- 82. Flow of control in a OO use case Application Services Customer Domain App Service App Service Validation Value Entity Infrastructure Entity Customer Repo. Value Email Message Value Database Service SMTP Service
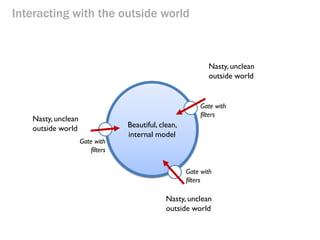
- 83. Interacting with the outside world Nasty, unclean outside world Nasty, unclean outside world Nasty, unclean outside world Beautiful, clean, internal model Gate with filters Gate with filters Gate with filters
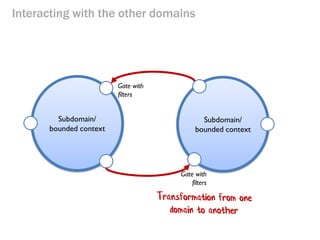
- 84. Interacting with the other domains Subdomain/ bounded context Gate with filters Subdomain/ bounded context Gate with filters
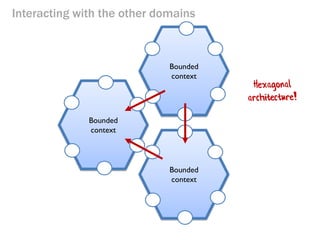
- 85. Interacting with the other domains Bounded context Bounded context Bounded context
- 87. Guideline: Parameterize all the things
- 88. Parameterize all the things let printList() = for i in [1..10] do printfn "the number is %i" i
- 89. Parameterize all the things It's second nature to parameterize the data input: let printList aList = for i in aList do printfn "the number is %i" i
- 90. Parameterize all the things let printList anAction aList = for i in aList do anAction i FPers would parameterize the action as well: We've decoupled the behavior from the data
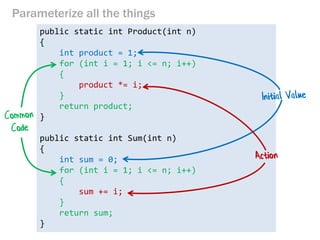
- 91. Parameterize all the things public static int Product(int n) { int product = 1; for (int i = 1; i <= n; i++) { product *= i; } return product; } public static int Sum(int n) { int sum = 0; for (int i = 1; i <= n; i++) { sum += i; } return sum; }
- 92. public static int Product(int n) { int product = 1; for (int i = 1; i <= n; i++) { product *= i; } return product; } public static int Sum(int n) { int sum = 0; for (int i = 1; i <= n; i++) { sum += i; } return sum; } Parameterize all the things
- 93. Parameterize all the things let product n = let initialValue = 1 let action productSoFar x = productSoFar * x [1..n] |> List.fold action initialValue let sum n = let initialValue = 0 let action sumSoFar x = sumSoFar+x [1..n] |> List.fold action initialValue Lots of collection functions like this: "fold", "map", "reduce", "collect", etc.
- 94. Guideline: Be as generic as possible
- 95. Generic code let printList anAction aList = for i in aList do anAction i // val printList : // ('a -> unit) -> seq<'a> -> unit Any kind of collection, any kind of action! F# and other functional languages make code generic automatically
- 96. Generic code int -> int How many ways are there to implement this function? 'a -> 'a How many ways are there to this function?
- 97. Generic code int list -> int list How many ways are there to implement this function? 'a list -> 'a list How many ways are there to this function?
- 98. Generic code ('a -> 'b) -> 'a list -> 'b list How many ways are there to implement this function?
- 99. Tip: Function types are "interfaces"
- 100. Function types are interfaces interface IBunchOfStuff { int DoSomething(int x); string DoSomethingElse(int x); void DoAThirdThing(string x); } Let's take the Single Responsibility Principle and the Interface Segregation Principle to the extreme... Every interface should have only one method!
- 101. Function types are interfaces interface IBunchOfStuff { int DoSomething(int x); } An interface with one method is a just a function type type IBunchOfStuff: int -> int Any function with that type is compatible with it let add2 x = x + 2 // int -> int let times3 x = x * 3 // int -> int
- 102. Strategy pattern is trivial in FP class MyClass { public MyClass(IBunchOfStuff strategy) {..} int DoSomethingWithStuff(int x) { return _strategy.DoSomething(x) } } Object-oriented strategy pattern: Functional equivalent: let DoSomethingWithStuff strategy x = strategy x
- 103. Decorator pattern in FP Functional equivalent of decorator pattern let add1 x = x + 1 // int -> int
- 104. Decorator pattern in FP Functional equivalent of decorator pattern let add1 x = x + 1 // int -> int let logged f x = printfn "input is %A" x let result = f x printfn "output is %A" result result
- 105. Decorator pattern in FP Functional equivalent of decorator pattern let add1 x = x + 1 // int -> int let logged f x = printfn "input is %A" x let result = f x printfn "output is %A" result result let add1Decorated = // int -> int logged add1 [1..5] |> List.map add1 [1..5] |> List.map add1Decorated
- 106. Tip Every function is a one parameter function
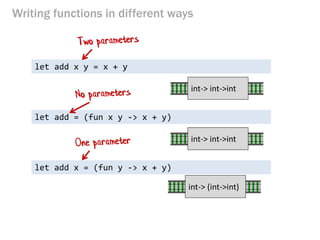
- 107. Writing functions in different ways let add x y = x + y let add = (fun x y -> x + y) let add x = (fun y -> x + y) int-> int->int int-> int->int int-> (int->int)
- 108. let three = 1 + 2 let add1 = (+) 1 let three = (+) 1 2 let add1ToEach = List.map add1
- 110. let names = ["Alice"; "Bob"; "Scott"] Names |> List.iter hello let name = "Scott" printfn "Hello, my name is %s" name let name = "Scott" (printfn "Hello, my name is %s") name let name = "Scott" let hello = (printfn "Hello, my name is %s") hello name
- 111. Pattern: Use partial application to do dependency injection
- 112. type GetCustomer = CustomerId -> Customer let getCustomerFromDatabase connection (customerId:CustomerId) = // from connection // select customer // where customerId = customerId type of getCustomerFromDatabase = DbConnection -> CustomerId -> Customer let getCustomer1 = getCustomerFromDatabase myConnection // getCustomer1 : CustomerId -> Customer Persistence agnostic
- 113. type GetCustomer = CustomerId -> Customer let getCustomerFromMemory map (customerId:CustomerId) = map |> Map.find customerId type of getCustomerFromMemory = Map<Id,Customer> -> CustomerId -> Customer let getCustomer2 = getCustomerFromMemory inMemoryMap // getCustomer2 : CustomerId -> Customer
- 114. Pattern: The Hollywood principle: continuations
- 115. Continuations int Divide(int top, int bottom) { if (bottom == 0) { throw new InvalidOperationException("div by 0"); } else { return top/bottom; } } Method has decided to throw an exception
- 116. Continuations void Divide(int top, int bottom, Action ifZero, Action<int> ifSuccess) { if (bottom == 0) { ifZero(); } else { ifSuccess( top/bottom ); } } Let the caller decide what happens what happens next?
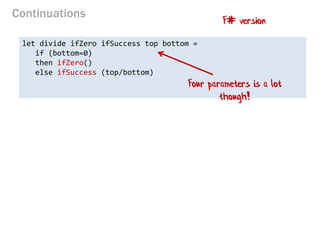
- 117. Continuations let divide ifZero ifSuccess top bottom = if (bottom=0) then ifZero() else ifSuccess (top/bottom) F# version Four parameters is a lot though!
- 118. Continuations let divide ifZero ifSuccess top bottom = if (bottom=0) then ifZero() else ifSuccess (top/bottom) let ifZero1 () = printfn "bad" let ifSuccess1 x = printfn "good %i" x let divide1 = divide ifZero1 ifSuccess1 //test let good1 = divide1 6 3 let bad1 = divide1 6 0 setup the functions to print a message Partially apply the continuations Use it like a normal function – only two parameters
- 119. Continuations let divide ifZero ifSuccess top bottom = if (bottom=0) then ifZero() else ifSuccess (top/bottom) let ifZero2() = None let ifSuccess2 x = Some x let divide2 = divide ifZero2 ifSuccess2 //test let good2 = divide2 6 3 let bad2 = divide2 6 0 setup the functions to return an Option Use it like a normal function – only two parameters Partially apply the continuations
- 120. Continuations let divide ifZero ifSuccess top bottom = if (bottom=0) then ifZero() else ifSuccess (top/bottom) let ifZero3() = failwith "div by 0" let ifSuccess3 x = x let divide3 = divide ifZero3 ifSuccess3 //test let good3 = divide3 6 3 let bad3 = divide3 6 0 setup the functions to throw an exception Use it like a normal function – only two parameters Partially apply the continuations
- 121. MONADS
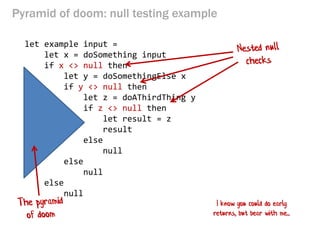
- 122. Pyramid of doom: null testing example let example input = let x = doSomething input if x <> null then let y = doSomethingElse x if y <> null then let z = doAThirdThing y if z <> null then let result = z result else null else null else null I know you could do early returns, but bear with me...
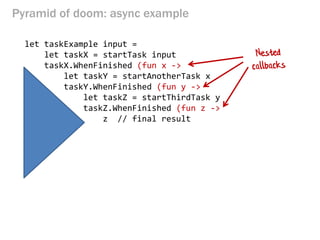
- 123. Pyramid of doom: async example let taskExample input = let taskX = startTask input taskX.WhenFinished (fun x -> let taskY = startAnotherTask x taskY.WhenFinished (fun y -> let taskZ = startThirdTask y taskZ.WhenFinished (fun z -> z // final result
- 124. Pyramid of doom: null example let example input = let x = doSomething input if x <> null then let y = doSomethingElse x if y <> null then let z = doAThirdThing y if z <> null then let result = z result else null else null else null Nulls are a code smell: replace with Option!
- 125. Pyramid of doom: option example let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None else None Much more elegant, yes? No! This is fugly! Let’s do a cut & paste refactoring
- 126. Pyramid of doom: option example let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None else None
- 127. Pyramid of doom: option example let doWithX x = let y = doSomethingElse x if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None let example input = let x = doSomething input if x.IsSome then doWithX x else None
- 128. Pyramid of doom: option example let doWithX x = let y = doSomethingElse x if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None let example input = let x = doSomething input if x.IsSome then doWithX x else None
- 129. Pyramid of doom: option example let doWithY y = let z = doAThirdThing y if z.IsSome then let result = z.Value Some result else None let doWithX x = let y = doSomethingElse x if y.IsSome then doWithY y else None let example input = let x = doSomething input if x.IsSome then doWithX x else None
- 130. Pyramid of doom: option example refactored let doWithZ z = let result = z Some result let doWithY y = let z = doAThirdThing y if z.IsSome then doWithZ z.Value else None let doWithX x = let y = doSomethingElse x if y.IsSome then doWithY y.Value else None let optionExample input = let x = doSomething input if x.IsSome then doWithX x.Value else None Three small pyramids instead of one big one! This is still ugly! But the code has a pattern...
- 131. Pyramid of doom: option example refactored let doWithZ z = let result = z Some result let doWithY y = let z = doAThirdThing y if z.IsSome then doWithZ z.Value else None let doWithX x = let y = doSomethingElse x if y.IsSome then doWithY y.Value else None let optionExample input = let x = doSomething input if x.IsSome then doWithX x.Value else None But the code has a pattern...
- 132. let doWithY y = let z = doAThirdThing y if z.IsSome then doWithZ z.Value else None
- 133. let doWithY y = let z = doAThirdThing y z |> ifSomeDo doWithZ let ifSomeDo f x = if x.IsSome then f x.Value else None
- 134. let doWithY y = y |> doAThirdThing |> ifSomeDo doWithZ let ifSomeDo f x = if x.IsSome then f x.Value else None
- 135. let example input = doSomething input |> ifSomeDo doSomethingElse |> ifSomeDo doAThirdThing |> ifSomeDo (fun z -> Some z) let ifSomeDo f x = if x.IsSome then f x.Value else None
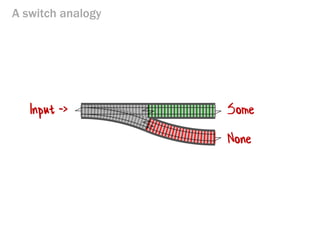
- 136. A switch analogy Some None Input ->
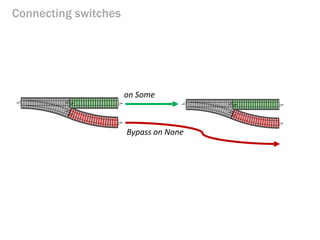
- 137. Connecting switches on Some Bypass on None
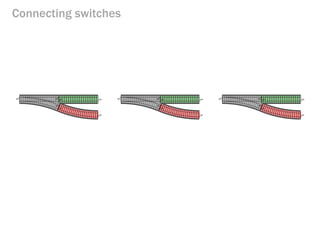
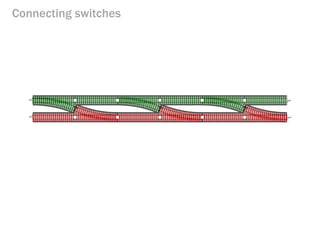
- 138. Connecting switches
- 139. Connecting switches
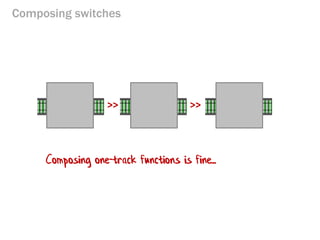
- 140. Composing switches >> >> Composing one-track functions is fine...
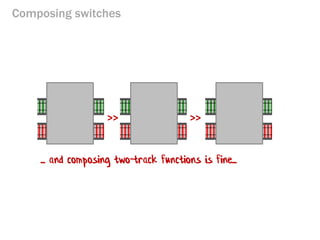
- 141. Composing switches >> >> ... and composing two-track functions is fine...
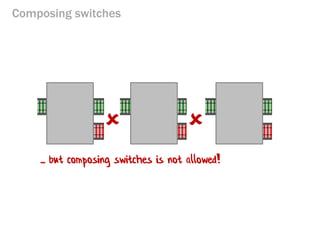
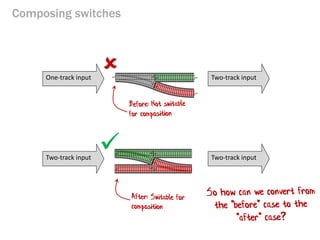
- 142. Composing switches ... but composing switches is not allowed!
- 143. Composing switches Two-track input Two-track input One-track input Two-track input
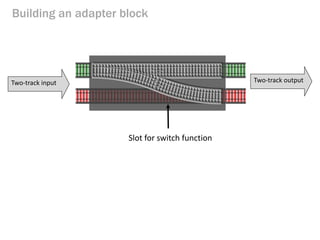
- 144. Building an adapter block Two-track input Slot for switch function Two-track output
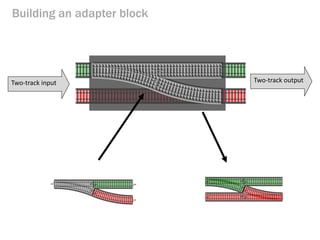
- 145. Building an adapter block Two-track input Two-track output
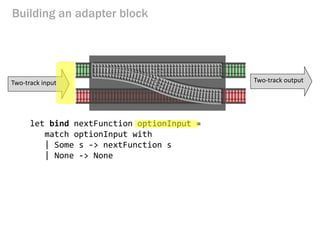
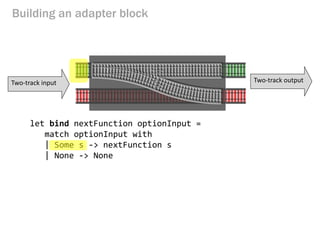
- 146. let bind nextFunction optionInput = match optionInput with | Some s -> nextFunction s | None -> None Building an adapter block Two-track input Two-track output
- 147. let bind nextFunction optionInput = match optionInput with | Some s -> nextFunction s | None -> None Building an adapter block Two-track input Two-track output
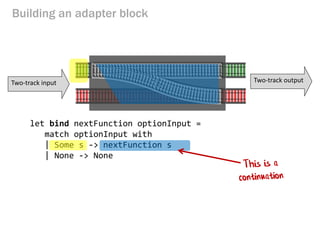
- 148. let bind nextFunction optionInput = match optionInput with | Some s -> nextFunction s | None -> None Building an adapter block Two-track input Two-track output
- 149. let bind nextFunction optionInput = match optionInput with | Some s -> nextFunction s | None -> None Building an adapter block Two-track input Two-track output
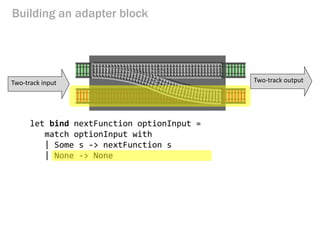
- 150. Pattern: Use bind to chain options
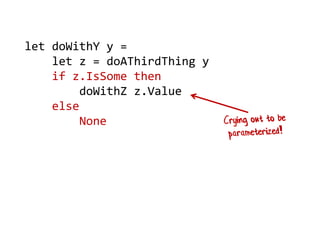
- 151. Pyramid of doom: using bind let bind f opt = match opt with | Some v -> f v | None -> None let example input = let x = doSomething input if x.IsSome then let y = doSomethingElse (x.Value) if y.IsSome then let z = doAThirdThing (y.Value) if z.IsSome then let result = z.Value Some result else None else None else None
- 152. let example input = doSomething input |> bind doSomethingElse |> bind doAThirdThing |> bind (fun z -> Some z) Pyramid of doom: using bind let bind f opt = match opt with | Some v -> f v | None -> None No pyramids! Code is linear and clear. This pattern is called “monadic bind”
- 153. Pattern: Use bind to chain tasks
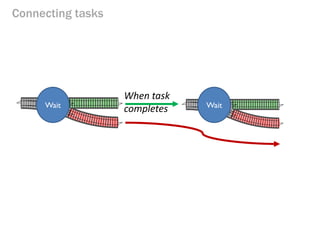
- 154. Connecting tasks When task completes Wait Wait
- 155. Pyramid of doom: using bind for tasks let taskBind f task = task.WhenFinished (fun taskResult -> f taskResult) let taskExample input = startTask input |> taskBind startAnotherTask |> taskBind startThirdTask |> taskBind (fun z -> z) a.k.a “promise” “future” This pattern is also a “monadic bind”
- 156. Computation expressions let example input = maybe { let! x = doSomething input let! y = doSomethingElse x let! z = doAThirdThing y return z } let taskExample input = task { let! x = startTask input let! y = startAnotherTask x let! z = startThirdTask z return z } Computation expression Computation expression
- 157. Pattern: Use bind to chain error handlers
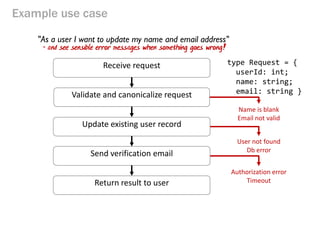
- 158. Example use case Name is blank Email not valid Receive request Validate and canonicalize request Update existing user record Send verification email Return result to user User not found Db error Authorization error Timeout "As a user I want to update my name and email address" type Request = { userId: int; name: string; email: string } - and see sensible error messages when something goes wrong!
- 159. Use case without error handling string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); validateRequest(request); canonicalizeEmail(request); db.updateDbFromRequest(request); smtpServer.sendEmail(request.Email) return "OK"; }
- 160. Use case with error handling string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); db.updateDbFromRequest(request); smtpServer.sendEmail(request.Email) return "OK"; }
- 161. Use case with error handling string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } smtpServer.sendEmail(request.Email) return "OK"; }
- 162. Use case with error handling string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); try { var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } } catch { return "DB error: Customer record not updated" } smtpServer.sendEmail(request.Email) return "OK"; }
- 163. Use case with error handling string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); try { var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } } catch { return "DB error: Customer record not updated" } if (!smtpServer.sendEmail(request.Email)) { log.Error "Customer email not sent" } return "OK"; }
- 164. Use case with error handling string UpdateCustomerWithErrorHandling() { var request = receiveRequest(); var isValidated = validateRequest(request); if (!isValidated) { return "Request is not valid" } canonicalizeEmail(request); try { var result = db.updateDbFromRequest(request); if (!result) { return "Customer record not found" } } catch { return "DB error: Customer record not updated" } if (!smtpServer.sendEmail(request.Email)) { log.Error "Customer email not sent" } return "OK"; }
- 165. A structure for managing errors Request Success Validate Failure let validateInput input = if input.name = "" then Failure "Name must not be blank" else if input.email = "" then Failure "Email must not be blank" else Success input // happy path type TwoTrack<'TEntity> = | Success of 'TEntity | Failure of string
- 166. name50 Bind example let nameNotBlank input = if input.name = "" then Failure "Name must not be blank" else Success input let name50 input = if input.name.Length > 50 then Failure "Name must not be longer than 50 chars" else Success input let emailNotBlank input = if input.email = "" then Failure "Email must not be blank" else Success input nameNotBlank emailNotBlank
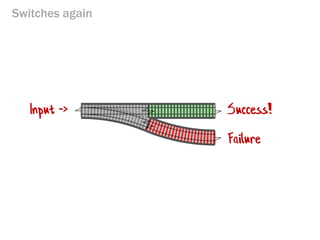
- 167. Switches again Success! Failure Input ->
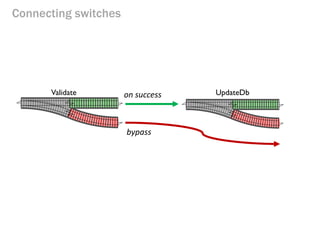
- 168. Connecting switches Validate UpdateDb on success bypass
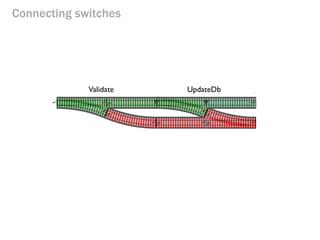
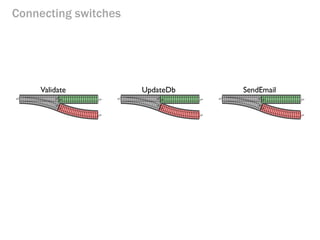
- 169. Connecting switches Validate UpdateDb
- 170. Connecting switches Validate UpdateDb SendEmail
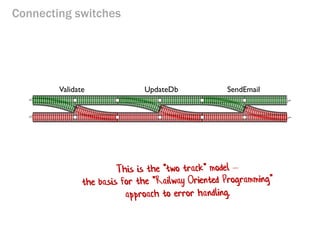
- 171. Connecting switches Validate UpdateDb SendEmail
- 172. Functional flow without error handling let updateCustomer = receiveRequest |> validateRequest |> canonicalizeEmail |> updateDbFromRequest |> sendEmail |> returnMessage Before One track
- 173. Functional flow with error handling let updateCustomerWithErrorHandling = receiveRequest |> validateRequest |> canonicalizeEmail |> updateDbFromRequest |> sendEmail |> returnMessage After See fsharpforfunandprofit.com/rop Two track
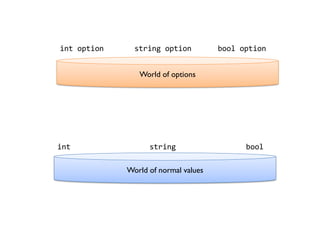
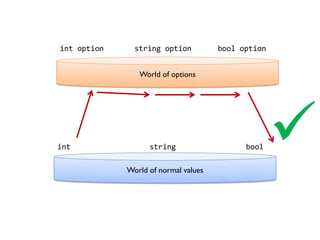
- 175. World of normal values int string bool World of options int option string option bool option
- 176. World of options World of normal values int string bool int option string option bool option
- 177. World of options World of normal values int string bool int option string option bool option
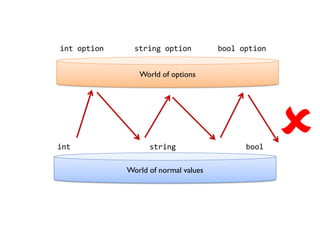
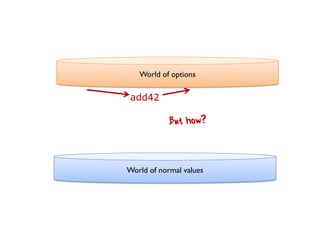
- 178. How not to code with options Let’s say you have an int wrapped in an Option, and you want to add 42 to it: let add42 x = x + 42 let add42ToOption opt = if opt.IsSome then let newVal = add42 opt.Value Some newVal else None
- 179. World of options World of normal values add42
- 180. World of options World of normal values add42
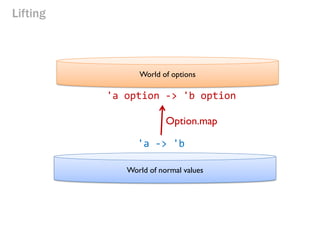
- 181. Lifting World of options World of normal values 'a -> 'b 'a option -> 'b option Option.map
- 182. The right way to code with options Let’s say you have an int wrapped in an Option, and you want to add 42 to it: let add42 x = x + 42 let add42ToOption = Option.map add42 Some 1 |> add42ToOption Some 1 |> Option.map add42
- 183. Pattern: Use “map” to lift functions
- 184. Lifting to lists World of lists World of normal values 'a -> 'b 'a list-> 'b list List.map
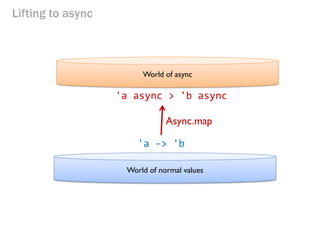
- 185. Lifting to async World of async World of normal values 'a -> 'b 'a async > 'b async Async.map
- 186. The right way to code with wrapped types Most wrapped types provide a “map” let add42 x = x + 42 Some 1 |> Option.map add42 [1;2;3] |> List.map add42
- 187. Guideline: If you create a wrapped generic type, create a “map” for it.
- 188. Maps type TwoTrack<'TEntity> = | Success of 'TEntity | Failure of string let mapTT f x = match x with | Success entity -> Success (f entity) | Failure s -> Failure s
- 189. Tip: Use applicatives for validation
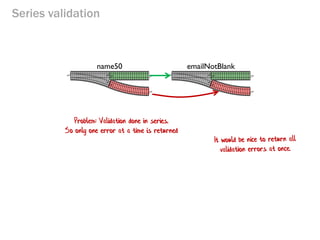
- 190. Series validation name50 emailNotBlank Problem: Validation done in series. So only one error at a time is returned
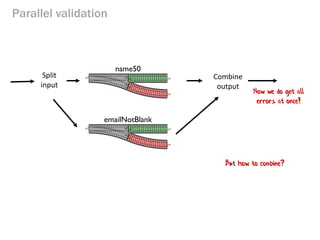
- 191. Parallel validation name50 emailNotBlank Split input Combine output Now we do get all errors at once! But how to combine?
- 192. Creating a valid data structure type Request= { UserId: UserId; Name: String50; Email: EmailAddress} type RequestDTO= { UserId: int; Name: string; Email: string}
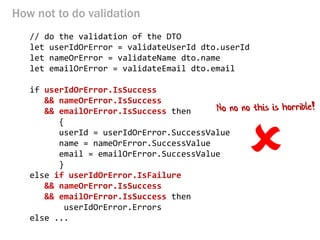
- 193. How not to do validation // do the validation of the DTO let userIdOrError = validateUserId dto.userId let nameOrError = validateName dto.name let emailOrError = validateEmail dto.email if userIdOrError.IsSuccess && nameOrError.IsSuccess && emailOrError.IsSuccess then { userId = userIdOrError.SuccessValue name = nameOrError.SuccessValue email = emailOrError.SuccessValue } else if userIdOrError.IsFailure && nameOrError.IsSuccess && emailOrError.IsSuccess then userIdOrError.Errors else ...
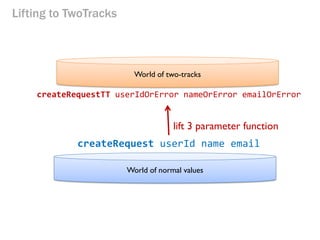
- 194. Lifting to TwoTracks World of two-tracks World of normal values createRequest userId name email createRequestTT userIdOrError nameOrError emailOrError lift 3 parameter function
- 195. The right way let createRequest userId name email = { userId = userIdOrError.SuccessValue name = nameOrError.SuccessValue email = emailOrError.SuccessValue } let createRequestTT = lift3 createRequest
- 196. The right way let createRequestTT = lift3 createRequest let userIdOrError = validateUserId dto.userId let nameOrError = validateName dto.name let emailOrError = validateEmail dto.email let requestOrError = createRequestTT userIdOrError nameOrError emailOrError
- 197. The right way let userIdOrError = validateUserId dto.userId let nameOrError = validateName dto.name let emailOrError = validateEmail dto.email let requestOrError = createRequest <!> userIdOrError <*> nameOrError <*> emailOrError
- 198. Guideline: If you use a wrapped generic type, look for a set of “lifts” associated with it
- 199. Guideline: If you create a wrapped generic type, also create a set of “lifts” for clients to use with it But I’m not going explain how right now!
- 200. MONOIDS
- 201. Mathematics Ahead
- 202. Thinking like a mathematician 1 + 2 = 3 1 + (2 + 3) = (1 + 2) + 3 1 + 0 = 1 0 + 1 = 1
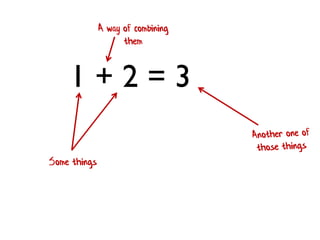
- 203. 1 + 2 = 3 Some things A way of combining them
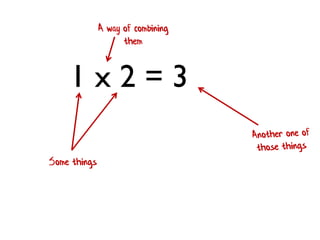
- 204. 2 x 3 = 6 Some things A way of combining them
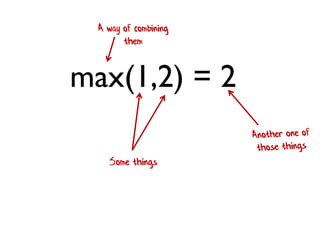
- 205. max(1,2) = 2 Some things A way of combining them
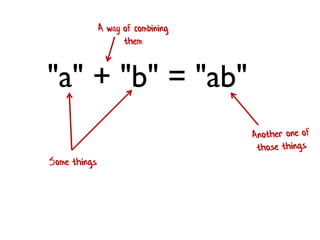
- 206. "a" + "b" = "ab" Some things A way of combining them
- 207. concat([a],[b]) = [a; b] Some things A way of combining them
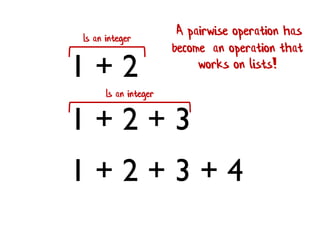
- 208. 1 + 2 1 + 2 + 3 1 + 2 + 3 + 4 Is an integer Is an integer A pairwise operation has become an operation that works on lists!
- 209. 1 + (2 + 3) = (1 + 2) + 3 Order of combining doesn’t matter 1 + 2 + 3 + 4 (1 + 2) + (3 + 4) ((1 + 2) + 3) + 4 All the same
- 210. 1 - (2 - 3) = (1 - 2) - 3 Order of combining does matter
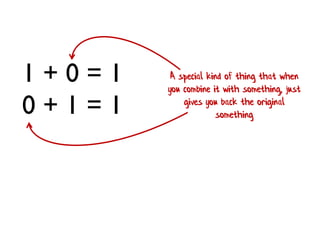
- 211. 1 + 0 = 1 0 + 1 = 1 A special kind of thing that when you combine it with something, just gives you back the original something
- 212. 42 * 1 = 42 1 * 42 = 42 A special kind of thing that when you combine it with something, just gives you back the original something
- 213. "" + "hello" = "hello" "hello" + "" = "hello" “Zero” for strings
- 214. The generalization •You start with a bunch of things, and some way of combining them two at a time. •Rule 1 (Closure): The result of combining two things is always another one of the things. •Rule 2 (Associativity): When combining more than two things, which pairwise combination you do first doesn't matter. •Rule 3 (Identity element): There is a special thing called "zero" such that when you combine any thing with "zero" you get the original thing back. A monoid!
- 215. •Rule 1 (Closure): The result of combining two things is always another one of the things. •Benefit: converts pairwise operations into operations that work on lists. 1 + 2 + 3 + 4 [ 1; 2; 3; 4 ] |> List.reduce (+)
- 216. 1 * 2 * 3 * 4 [ 1; 2; 3; 4 ] |> List.reduce (*) •Rule 1 (Closure): The result of combining two things is always another one of the things. •Benefit: converts pairwise operations into operations that work on lists.
- 217. "a" + "b" + "c" + "d" [ "a"; "b"; "c"; "d" ] |> List.reduce (+) •Rule 1 (Closure): The result of combining two things is always another one of the things. •Benefit: converts pairwise operations into operations that work on lists.
- 218. •Rule 2 (Associativity): When combining more than two things, which pairwise combination you do first doesn't matter. •Benefit: Divide and conquer, parallelization, and incremental accumulation. 1 + 2 + 3 + 4
- 219. •Rule 2 (Associativity): When combining more than two things, which pairwise combination you do first doesn't matter. •Benefit: Divide and conquer, parallelization, and incremental accumulation. (1 + 2) (3 + 4) 3 + 7
- 220. •Rule 2 (Associativity): When combining more than two things, which pairwise combination you do first doesn't matter. •Benefit: Divide and conquer, parallelization, and incremental accumulation. (1 + 2 + 3)
- 221. •Rule 2 (Associativity): When combining more than two things, which pairwise combination you do first doesn't matter. •Benefit: Divide and conquer, parallelization, and incremental accumulation. (1 + 2 + 3) + 4
- 222. •Rule 2 (Associativity): When combining more than two things, which pairwise combination you do first doesn't matter. •Benefit: Divide and conquer, parallelization, and incremental accumulation. (6) + 4
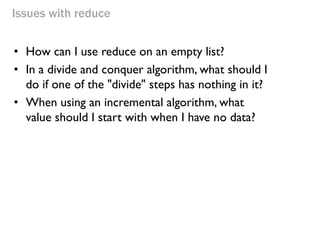
- 223. Issues with reduce •How can I use reduce on an empty list? •In a divide and conquer algorithm, what should I do if one of the "divide" steps has nothing in it? •When using an incremental algorithm, what value should I start with when I have no data?
- 224. •Rule 3 (Identity element): There is a special thing called "zero" such that when you combine any thing with "zero" you get the original thing back. •Benefit: Initial value for empty or missing data
- 225. Pattern: Simplifying aggregation code with monoids
- 226. type OrderLine = {Qty:int; Total:float} let orderLines = [ {Qty=2; Total=19.98} {Qty=1; Total= 1.99} {Qty=3; Total= 3.99} ] let addLine line1 line2 = let newQty = line1.Qty + line2.Qty let newTotal = line1.Total + line2.Total {Qty=newQty; Total=newTotal} orderLines |> List.reduce addLine Any combination of monoids is also a monoid
- 227. Pattern: Convert non-monoids to monoids
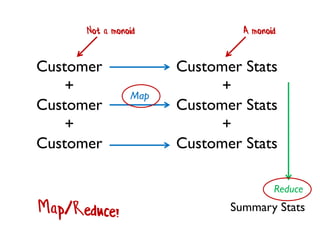
- 228. Customer + Customer + Customer Customer Stats + Customer Stats + Customer Stats Reduce Map Not a monoid A monoid Summary Stats
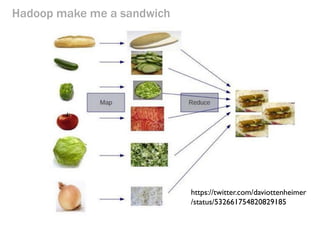
- 229. Hadoop make me a sandwich https://twitter.com/daviottenheimer/status/532661754820829185
- 230. Guideline: Convert expensive monoids to cheap monoids
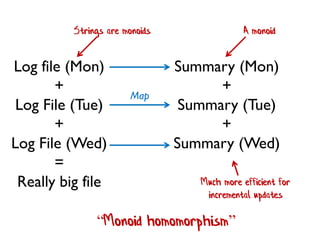
- 231. Log file (Mon) + Log File (Tue) + Log File (Wed) = Really big file Summary (Mon) + Summary (Tue) + Summary (Wed) Map Strings are monoids A monoid Much more efficient for incremental updates “Monoid homomorphism”
- 232. Pattern: Seeing monoids everywhere
- 233. Monoids in the real world Metrics guideline: Use counters rather than rates Alternative metrics guideline: Make sure your metrics are monoids • incremental updates • can handle missing data
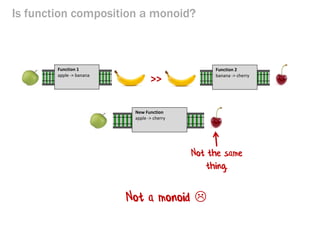
- 234. Is function composition a monoid? >> Function 1 apple -> banana Function 2 banana -> cherry New Function apple -> cherry Not the same thing. Not a monoid
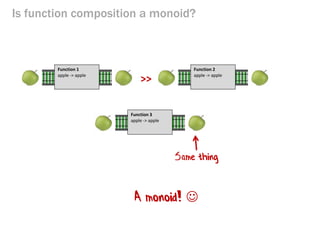
- 235. Is function composition a monoid? >> Function 1 apple -> apple Same thing Function 2 apple -> apple Function 3 apple -> apple A monoid!
- 236. Is function composition a monoid? “Functions with same type of input and output” Functions where the input and output are the same type are monoids! What shall we call these kinds of functions?
- 237. Is function composition a monoid? “Functions with same type of input and output” “Endomorphisms” Functions where the input and output are the same type are monoids! What shall we call these kinds of functions? All endomorphisms are monoids
- 238. Endomorphism example let plus1 x = x + 1 // int->int let times2 x = x * 2 // int->int let subtract42 x = x – 42 // int->int let functions = [ plus1 times2 subtract42 ] let newFunction = // int->int functions |> List.reduce (>>) newFunction 20 // => 0 Endomorphisms Put them in a list Reduce them Another endomorphism
- 239. Event sourcing Any function containing an endomorphism can be converted into a monoid. For example: Event sourcing Is an endomorphism Event -> State -> State
- 240. Event sourcing example let applyFns = [ apply event1 // State -> State apply event2 // State -> State apply event3] // State -> State let applyAll = // State -> State applyFns |> List.reduce (>>) let newState = applyAll oldState • incremental updates • can handle missing events Partial application of event A function that can apply all the events in one step
- 241. Bind Any function containing an endomorphism can be converted into a monoid. For example: Option.Bind Is an endomorphism (fn param) -> Option -> Option
- 242. Event sourcing example let bindFns = [ Option.bind (fun x-> if x > 1 then Some (x*2) else None) Option.bind (fun x-> if x < 10 then Some x else None) ] let bindAll = // Option->Option bindFns |> List.reduce (>>) Some 4 |> bindAll // Some 8 Some 5 |> bindAll // None Partial application of Bind
- 243. Predicates as monoids type Predicate<'A> = 'A -> bool let predAnd pred1 pred2 x = if pred1 x then pred2 x else false let predicates = [ isMoreThan10Chars // string -> bool isMixedCase // string -> bool isNotDictionaryWord // string -> bool ] let combinedPredicate = // string -> bool predicates |> List.reduce (predAnd) Not an endomorphism But can still be combined
- 244. Pattern: Monads are monoids
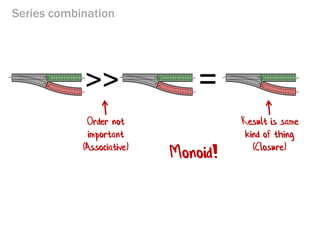
- 245. Series combination = >> Result is same kind of thing (Closure) Order not important (Associative) Monoid!
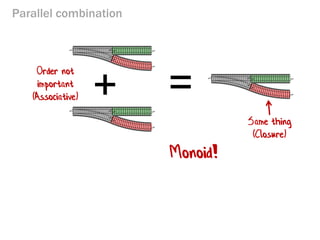
- 246. Parallel combination = + Same thing (Closure) Order not important (Associative) Monoid!
- 247. Monad laws •The Monad laws are just the monoid definitions in diguise –Closure, Associativity, Identity •What happens if you break the monad laws? –You lose monoid benefits such as aggregation
- 248. A monad is just a monoid in the category of endofunctors!
- 249. THANKS!


























































![Parameterize all the things
let printList() =
for i in [1..10] do
printfn "the number is %i" i](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-88-320.jpg)



![Parameterize all the things
let product n =
let initialValue = 1
let action productSoFar x = productSoFar * x
[1..n] |> List.fold action initialValue
let sum n =
let initialValue = 0
let action sumSoFar x = sumSoFar+x
[1..n] |> List.fold action initialValue
Lots of collection functions like this: "fold", "map", "reduce", "collect", etc.](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-93-320.jpg)











![Decorator pattern in FP
Functional equivalent of decorator pattern
let add1 x = x + 1 // int -> int
let logged f x =
printfn "input is %A" x
let result = f x
printfn "output is %A" result
result
let add1Decorated = // int -> int
logged add1
[1..5] |> List.map add1
[1..5] |> List.map add1Decorated](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-105-320.jpg)



![let names = ["Alice"; "Bob"; "Scott"]
Names |> List.iter hello
let name = "Scott"
printfn "Hello, my name is %s" name
let name = "Scott"
(printfn "Hello, my name is %s") name
let name = "Scott"
let hello = (printfn "Hello, my name is %s")
hello name](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-110-320.jpg)












































![The right way to code with wrapped types
Most wrapped types provide a “map”
let add42 x = x + 42
Some 1 |> Option.map add42
[1;2;3] |> List.map add42](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-186-320.jpg)











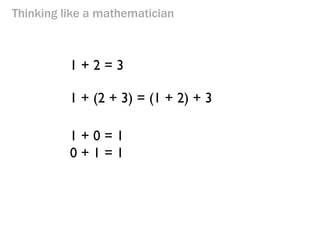
![concat([a],[b]) = [a; b]
Some things
A way of combining them](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-207-320.jpg)


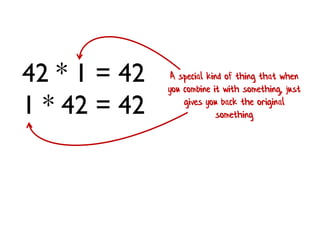


![•Rule 1 (Closure): The result of combining two things is always another one of the things.
•Benefit: converts pairwise operations into operations that work on lists.
1 + 2 + 3 + 4
[ 1; 2; 3; 4 ] |> List.reduce (+)](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-215-320.jpg)
![1 * 2 * 3 * 4
[ 1; 2; 3; 4 ] |> List.reduce (*)
•Rule 1 (Closure): The result of combining two things is always another one of the things.
•Benefit: converts pairwise operations into operations that work on lists.](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-216-320.jpg)
!["a" + "b" + "c" + "d"
[ "a"; "b"; "c"; "d" ] |> List.reduce (+)
•Rule 1 (Closure): The result of combining two things is always another one of the things.
•Benefit: converts pairwise operations into operations that work on lists.](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-217-320.jpg)







![type OrderLine = {Qty:int; Total:float}
let orderLines = [
{Qty=2; Total=19.98}
{Qty=1; Total= 1.99}
{Qty=3; Total= 3.99} ]
let addLine line1 line2 =
let newQty = line1.Qty + line2.Qty
let newTotal = line1.Total + line2.Total
{Qty=newQty; Total=newTotal}
orderLines |> List.reduce addLine
Any combination of monoids is also a monoid](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-226-320.jpg)






![Endomorphism example
let plus1 x = x + 1 // int->int
let times2 x = x * 2 // int->int
let subtract42 x = x – 42 // int->int
let functions = [
plus1
times2
subtract42 ]
let newFunction = // int->int
functions |> List.reduce (>>)
newFunction 20 // => 0
Endomorphisms
Put them in a list
Reduce them
Another endomorphism](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-238-320.jpg)

![Event sourcing example
let applyFns = [
apply event1 // State -> State
apply event2 // State -> State
apply event3] // State -> State
let applyAll = // State -> State
applyFns |> List.reduce (>>)
let newState = applyAll oldState
• incremental updates
• can handle missing events
Partial application of event
A function that can apply all the events in one step](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-240-320.jpg)

![Event sourcing example
let bindFns = [
Option.bind (fun x->
if x > 1 then Some (x*2) else None)
Option.bind (fun x->
if x < 10 then Some x else None)
]
let bindAll = // Option->Option
bindFns |> List.reduce (>>)
Some 4 |> bindAll // Some 8
Some 5 |> bindAll // None
Partial application of Bind](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-242-320.jpg)
![Predicates as monoids
type Predicate<'A> = 'A -> bool
let predAnd pred1 pred2 x =
if pred1 x
then pred2 x
else false
let predicates = [
isMoreThan10Chars // string -> bool
isMixedCase // string -> bool
isNotDictionaryWord // string -> bool
]
let combinedPredicate = // string -> bool
predicates |> List.reduce (predAnd)
Not an endomorphism
But can still be combined](https://image.slidesharecdn.com/j6neru4mrj6ivbemoazk-signature-2dc2444de4bab674e57017541f6665ded1bda52727a96fc1951b3c3f5300cafc-poli-141124002944-conversion-gate02/85/Functional-Programming-Patterns-BuildStuff-14-243-320.jpg)