Donutsプロコンチャレンジ 2015 解説
- 2. おつかれさまでした!
- 3. 問題A ドーナツの体積
- 11. 問題B 解答 for(i = 0; i < 2^n; i++){ }
- 12. 問題B 解答 for(i = 0; i < 2^n; i++){ if(iのビットが立っている数が9個){ } }
- 13. 問題B 解答 for(i = 0; i < 2^n; i++){ if(iのビットが立っている数が9個){ // 結果が大きければ更新 } }
- 14. 問題C 行列のできるドーナツ屋
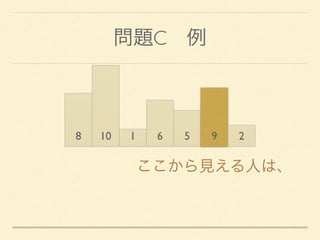
- 16. 問題C 例 8 10 1 6 5 9 2
- 17. 問題C 例 8 10 1 6 5 9 2 ここから見える人は、
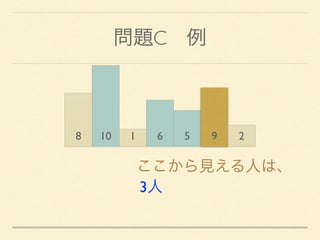
- 18. 問題C 例 8 10 1 6 5 9 2 ここから見える人は、 3人
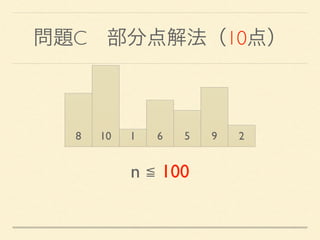
- 19. 問題C 部分点解法(10点) 8 10 1 6 5 9 2 n ≦ 100
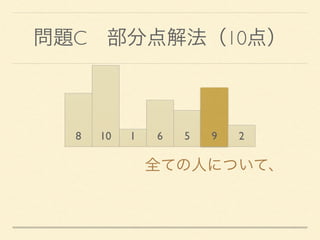
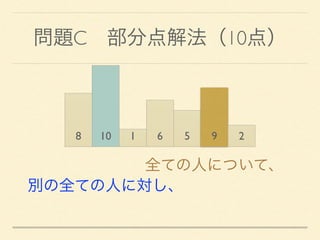
- 20. 問題C 部分点解法(10点) 8 10 1 6 5 9 2 全ての人について、
- 21. 問題C 部分点解法(10点) 8 10 1 6 5 9 2 全ての人について、 別の全ての人に対し、
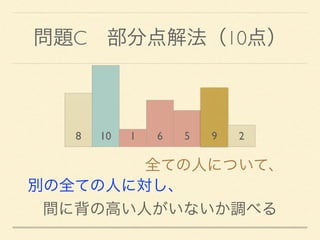
- 22. 問題C 部分点解法(10点) 8 10 1 6 5 9 2 全ての人について、 別の全ての人に対し、 間に背の高い人がいないか調べる
- 23. 問題C 部分点解法(10点) 8 10 1 6 5 9 2 O(n^3)
- 24. 問題C 部分点解法(40点) 8 10 1 6 5 9 2 n ≦ 5000
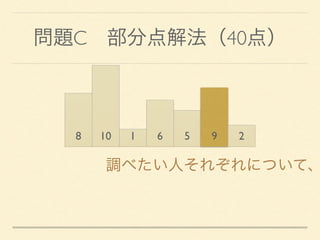
- 25. 問題C 部分点解法(40点) 8 10 1 6 5 9 2 調べたい人それぞれについて、
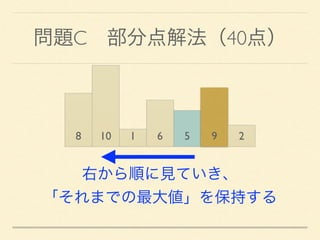
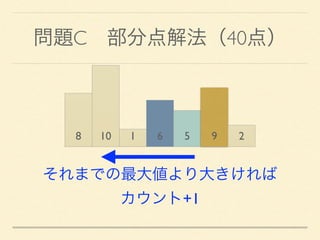
- 26. 問題C 部分点解法(40点) 8 10 1 6 5 9 2 右から順に見ていき、 「それまでの最大値」を保持する
- 27. 問題C 部分点解法(40点) 8 10 1 6 5 9 2 それまでの最大値より大きければ カウント+1
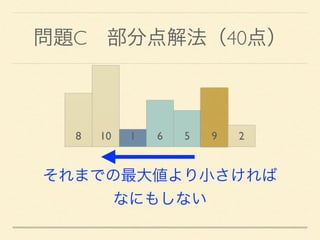
- 28. 問題C 部分点解法(40点) 8 10 1 6 5 9 2 それまでの最大値より小さければ なにもしない
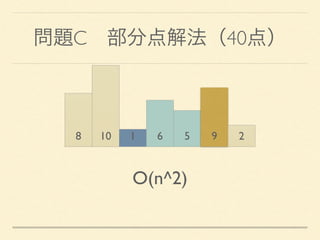
- 29. 問題C 部分点解法(40点) 8 10 1 6 5 9 2 O(n^2)
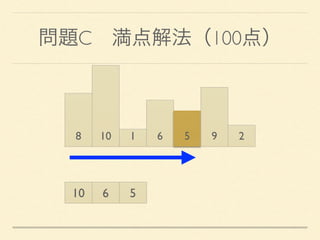
- 30. 問題C 満点解法(100点) 8 10 1 6 5 9 2 n ≦ 100000
- 31. 問題C 満点解法(100点) 8 10 1 6 5 9 2 n ≦ 100000 スタックを用いてO(n)で解く
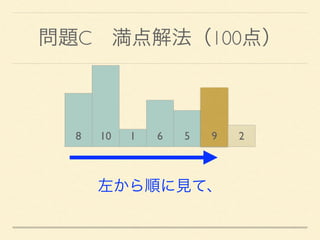
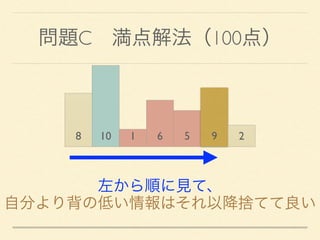
- 32. 問題C 満点解法(100点) 8 10 1 6 5 9 2 左から順に見て、
- 33. 問題C 満点解法(100点) 8 10 1 6 5 9 2 左から順に見て、 自分より背の低い情報はそれ以降捨てて良い
- 34. 問題C 満点解法(100点) 8 10 1 6 5 9 2 8
- 35. 問題C 満点解法(100点) 8 10 1 6 5 9 2 8 10
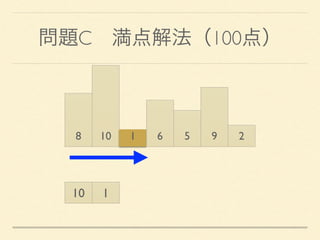
- 36. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10
- 37. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10 1
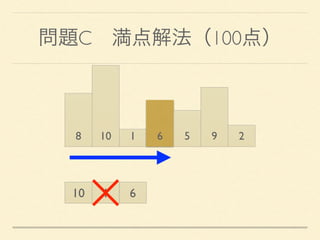
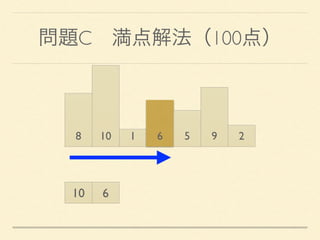
- 38. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10 1 6
- 39. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10 6
- 40. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10 6 5
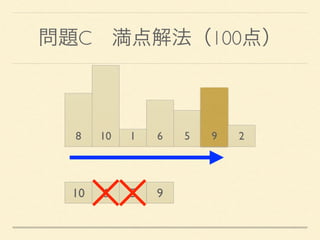
- 41. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10 6 5 9
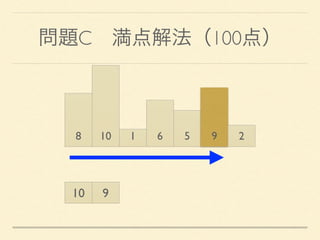
- 42. 問題C 満点解法(100点) 8 10 1 6 5 9 2 10 9
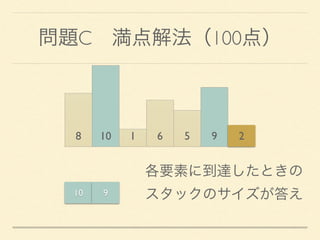
- 43. 問題C 満点解法(100点) 8 10 1 6 5 9 2 各要素に到達したときの スタックのサイズが答え10 9
- 44. 問題C 満点解法(100点) 8 10 1 6 5 9 2 ・「スタックに追加する」 ・「スタックから取り除く」 いずれも高々n回 → O(n)
- 45. 問題D ドーナツの箱詰め
- 46. 問題D 1 ≦ n ≦ 200000 要素を、kグループに分ける 「各グループの(最大値 − 最小値)の和」 の最小値は?
- 47. 問題D 例 k = 3 {2, 12, 3, 13, 7, 17, 1}
- 48. 問題D 例 k = 3 {2, 12, 3, 13, 7, 17, 1} {1, 2, 3, 7} {12, 13} {17} 6+1+0 = 7 が最小値
- 49. 問題D 例 k = 3 {2, 12, 3, 13, 7, 17, 1} どんな入力であっても、
- 50. 問題D 例 k = 3 {1, 2, 3, 7, 12, 13, 17} どんな入力であっても、 ソートしておき、
- 51. 問題D 例 k = 3 {1, 2, 3, 7, 12, 13, 17} どんな入力であっても、 ソートしておき、 重ならない区間でグループ分けする ことが最小値の必要条件
- 52. 問題D 部分点解法(15点) {1, 2, 3, 7, 12, 13, 17} k = 2
- 53. 問題D 部分点解法(15点) {1, 2, 3, 7, 12, 13, 17} k = 2 ソート後、グループ分けの候補を n-1通り試せば良い
- 54. 問題D 部分点解法(40点) {1, 2, 3, 7, 12, 13, 17} 1 ≦ k ≦ n
- 55. 問題D 部分点解法(40点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 1 4 各要素の差からなる(n-1)要素を準備
- 56. 問題D 部分点解法(40点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 1 4 各要素の差からなる(n-1)要素を準備 グループ分けした時、差の要素のうち (k-1)要素は含まれない k = 3
- 57. 問題D 部分点解法(40点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 1 4 小さい方から(n-1)-(k-1) = n-k個 を選べば良い k = 3
- 58. 問題D 部分点解法(45点) k = 2 {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 1 4
- 59. 問題D 部分点解法(45点) k = 2 {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 5 “差の要素”が減っていく
- 60. 問題D 部分点解法(45点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 5 もとの要素はsetや隣接リストなどで持っておき、 要素がなくなった時に消える“差”と追加される“差” を計算する。
- 61. 問題D 部分点解法(45点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 5 “差”の要素はmultisetなどで持っておき、 “差の合計”から“差の最大値”を引けば良い。
- 62. 問題D 満点解法(100点) 1 ≦ k ≦ n {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 5 “差の要素”が減っていく
- 63. 問題D 満点解法(100点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 5 ・“差の要素”に数Xを追加する/取り除く ・“差の要素”の小さいn-k個の和を求める という操作を高速に行う
- 64. 問題D 満点解法(100点) {1, 2, 3, 7, 12, 13, 17} 1 1 4 5 5 ・“差の要素”に数Xを追加する/取り除く ・“差の要素”の小さいn-k個の和を求める という操作を高速に行う Segment Tree
- 65. 0 1 2 3 4 5 6 7 各ノードは、“差の要素”の 「個数」と「和」の情報をもつ。
- 66. 0 1 2 3 4 5 6 7 “差の要素”の中に、4∼7は、 現在いくつ持っていて、その合計はいくつか?
- 67. 0 1 2 3 4 5 6 7 2・3は、現在いくつ持っていて、 その合計はいくつか?
- 68. 1000 1001 1010 1011 1100 1101 1110 1111 100 101 110 111 10 11 1 0 1 2 3 4 5 6 7 ノード番号(2進)
- 69. 1000 1001 1010 1011 1100 1101 1110 1111 100 101 110 111 10 11 1 0 1 2 3 4 5 6 7 左の子を見るときは、2倍する
- 70. 1000 1001 1010 1011 1100 1101 1110 1111 100 101 110 111 10 11 1 0 1 2 3 4 5 6 7 右の子を見るときは、2倍して1足す
- 71. 1000 1001 1010 1011 1100 1101 1110 1111 100 101 110 111 10 11 1 0 1 2 3 4 5 6 7 親を見るときは、2で割る
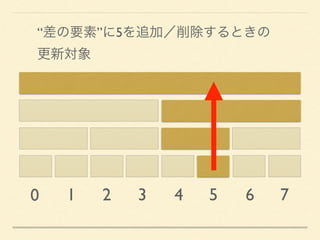
- 72. 0 1 2 3 4 5 6 7 “差の要素”に5を追加/削除するときの 更新対象
- 73. 0 1 2 3 4 5 6 7 「小さい方からX個の合計」を求める
- 74. 0 1 2 3 4 5 6 7 左の子(0∼3)がX個以上持っていれば、
- 75. 0 1 2 3 4 5 6 7 左の子(0∼3)がX個以上持っていれば、 再帰的に左の子より下を引き続き見る
- 76. 0 1 2 3 4 5 6 7 左の子(0∼3)がX個未満(Y個)であれば、
- 77. 0 1 2 3 4 5 6 7 左の子(0∼3)がX個未満(Y個)であれば、 左の子(0∼3)の合計値は必ず使用し、
- 78. 0 1 2 3 4 5 6 7 左の子(0∼3)がX個未満(Y個)であれば、 左の子(0∼3)の合計値は必ず使用し、 右の子(4∼7)の小さい方からX-Y個を取得
- 81. ありがとうございました!