Introduction to Persistence Theory

Copyright © 2016 NTT DATA Mathematical Systems Inc.
2017/02/25 第 2 回数理生物カフェ
s.t.@simizut22
Introduction to Persistence Theory

2Copyright © 2016 NTT DATA Mathematical Systems Inc.
目次
• Persistent Homology/Module #とは
• Persistent Homology の表示方法
• Stability

Copyright © 2016 NTT DATA Mathematical Systems Inc. 3
Persistent Homology #とは

距離空間
Def
𝑋, 𝑑 : が距離空間
⇔
𝑑: 𝑋 × 𝑋 → ℝ≥0 は次を満たす関数
𝑑(𝑥, 𝑦) = 𝑑(𝑦, 𝑥)
𝑑 𝑥, 𝑦 = 0 ⇔ 𝑥 = 𝑦
𝑑 𝑥, 𝑧 ≤ 𝑑 𝑥, 𝑦 + 𝑑(𝑦, 𝑧)

距離空間
例1 (ユークリッド空間)
𝑋 = ℝ 𝑁, 𝑑 𝑥, 𝑦 = ∑ 𝑥𝑖 − 𝑦𝑖
2
例2 (文字列の空間)
Σ: 文字の集合とし、 𝑋 を Σ 上の長さ 𝑁 の文字列のなす集合とする。
𝑋 = { 𝑥𝑖 𝑖=0
𝑁
∣ 𝑥𝑖 ∈ Σ }
𝑑: 𝑋 × 𝑋 → ℝ を次で与える：
𝑑 𝑥, 𝑦 = #{ 𝑖 ∣ 𝑥𝑖 ≠ 𝑦𝑖 }
これは 𝑋 上の距離になる□

問題設定
さて、
𝑌, 𝑑 を距離空間とし、 𝑋 ⊂ 𝑌 を有限集合とする(point cloud という)
𝑋 がどのような空間/モデルから生成されたデータなのか、何かしらの情報
を 𝑋 から知りたい
例：
- 次元
- 連結度

問題設定
一つの道具としての Persistent Homology
• 一般的に平面上なら簡単だが，入力の次元が高次元になると大変．
• Persistent Homology はデータの次元によらない

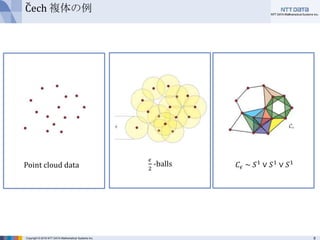
Cech複体
Def(Cech 複体)
𝑟 > 0 に対し、
𝐶 𝑘 𝑌, 𝑟 ≔ { 𝑖0, … , 𝑖 𝑘 ∣ ∩𝑗 𝐵 𝑦𝑖 𝑗
, 𝑟 ≠ 𝜙 }
を 𝑘-単体の集合として、これは抽象単体複体を与える
これをCech 複体という□

Cech 複体の例
𝜖
2
-ballsPoint cloud data 𝐶𝜖 ~ 𝑆1 ∨ 𝑆1 ∨ 𝑆1

Cech 複体の正当性
以下の定理が成立する
Thm
M をコンパクトリーマン多様体とする．このとき、𝜀 > 0 が存在し
任意の 0 < ∀𝑒 ≤ 𝜀 に対し、 𝑉 ⊂ 𝑀: 有限集合が存在し
𝐶∗ 𝑉, 𝑒 ∼ℎ.𝑒. 𝑀
よい性質をあらわしていてくれていることを期待できそう？？

Cech 複体の代替
Cech 複体は理論的には素晴らしいが、組み合わせ的な構造により計算的に
は困難が生じる。
Def(Vietoris-Rips 複体)
𝑟 > 0 に対し、
𝑉𝑅 𝑘 𝑌, 𝑟 ≔ { 𝑖0, … , 𝑖 𝑘 ∣ 𝑑(𝑦𝑖 𝑎
, 𝑦𝑖 𝑏
) < 2𝑟}
を 𝑘-単体の集合として、これは抽象単体複体を与える
これをVietoris-Rips 複体という□
こっちは簡単に計算できる(pt cloud に関する距離の matrix だけで可能)

Vietoris-Rips 複体の例
𝜖
2
-ballsPoint cloud data 𝑅 𝜖 ~ 𝑆1
∨ 𝑆2

Vietoris-Rips 複体の正当性
定義から明らかに
𝐶∗ 𝑟 ⊂ 𝑉𝑅∗(𝑟)
だが、実際には次も成立
Prop
𝑉𝑅∗ 𝑟 ⊂ 𝐶∗ 2 𝑟
よって、(各 r ではなく) r の“増大列”
0 = 𝑟0 < 𝑟1 < ⋯ < 𝑟𝑛 < ⋯
に対し、𝑉𝑅∗ や 𝐶∗ の系列を考えるのであれば本質的に同じと思える

1. Rips 複体の列

homology
𝐶 𝑘 を 𝑉𝑅 𝑘 (または 𝐶 𝑘 )が生成する 𝕜-ベクトル空間とする
このとき、境界準同型 𝜕: 𝐶 𝑘 → 𝐶 𝑘−1 が次で定まる
𝜕(𝑖0, . . , 𝑖 𝑘) = ∑ −1 𝑎
(𝑖0, … , 𝑖 𝑎, … , 𝑖 𝑘)
𝜕 ∘ 𝜕 = 0
すなわち
Im𝜕 𝑘+1 ⊂ Ker𝜕 𝑘
であることが分かるので，この商をとる：
Hk C∗ : =
Ker𝜕 𝑘
Im𝜕 𝑘+1
これを k-次ホモロジー群という

homology の性質
1. Functorial(関手性)
特に、
包含写像 𝑖: 𝐶∗ ↪ 𝐷∗ により準同型
𝐻 𝑘 𝑖 : 𝐻 𝑘 𝐶∗ → 𝐻 𝑘(𝐷∗)
が誘導され、次の自然性を持つ
𝑖: 𝐶∗ → 𝐷∗, 𝑗: 𝐷∗ → 𝐸∗ に対し
𝐻 𝑘 𝑗 ∘ 𝑖 = 𝐻 𝑘 𝑗 ∘ 𝐻 𝑘 𝑖
2. Homotopy 不変(または位相不変)
今日は明示的には使わないので略

Persistent Homology/Module
𝑟0 < 𝑟1 < ⋯ < 𝑟𝑛 < ⋯ < rN という列に対し Vietoris-Rips 複体の列をとる：
𝑉𝑅∗ 𝑟0 ↪ 𝑉𝑅∗ 𝑟1 ↪ ⋯ ↪ 𝑉𝑅∗(𝑟 𝑁)
これは Homology の関手性から次のベクトル空間の図式を導く
i.e.
𝑃𝐻 𝑘: 𝐻 𝑘 𝑉𝑅∗ 𝑟0 → 𝐻 𝐾 𝑉𝑅∗ 𝑟1 → ⋯ → 𝐻 𝑘(𝑉𝑅∗ 𝑟 𝑁 )
def
上で構成したベクトル空間の図式 𝑃𝐻 𝑘 を Persistent Homology という．
また一般に，上のような図式を 𝑁 -indexed Persistent Module という
ここで， 𝑁 = {0, 1, … , 𝑁}

Persistent Homology/Module
Persistent Module において何が重要か？？
矢印がどのくらい同型から外れるか
その点で
ある homology クラスは死に
ある homology クラスは生まれる
と思える
逆に、(有限型の) Persistent Module はこのデータから (up-to-iso) で一意に
特徴づけられる → 次章で説明

Persistent Homology の表示

Interval Module
Def(Interval Module)
0 ≤ 𝑏 ≤ 𝑑 ≤ 𝑁 に対し Persistent Module 𝐼[𝑏,𝑑] を次の図式で与える：
𝐼 𝑖,𝑗 : 0 = 0 … 0 → 𝕜
𝑏
= 𝕜 = ⋯ = 𝕜
𝑑
→ 0 = ⋯ = 0
これを Interval Module という
これは時刻 b で発生し時刻 d まで生きる homology class に対応する
module

分解定理
Thm(Gabriel, Krull-Schmidt)
Persistent Module は次のような Interval Module による分解を持つ:
𝑃𝐻 𝑘 ≅⊕ 𝑗 𝐼[𝑏 𝑗,𝑑 𝑗]
この直和分解は区間 [𝑏𝑗, 𝑑𝑗] の index の付け替えを除いて一意
PH に対し、Interval Decomposition を行いそれを横棒の形で並べたものを
Barcode という

bar-code の例

分解定理の remark
Interval Decomposition 定理は
- ℝ, ≤ -indexed tame module
- 離散 indexed zigzag persistent module
でも成立
これは
1 変数多項式環 𝕜 𝑡 が単項イデアル整域(PID)であることによる ■

Stability Theorem

Barcode の空間の距離構造
𝔅 を barcode 全体の空間とする。i.e. ℝ2
内の点の multiset 全体の集合
𝔅 には次の bottleneck distance という“距離” が定まる
𝑑 𝐵 𝐷, 𝐸 = inf
𝛾
sup
𝑥∈𝐷∪Δ
𝑥 − 𝛾(𝑥) ∞
ここで 𝛾 は
{𝑏𝑖𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝛾: 𝐷 ∪ ∃
𝐴 → 𝐸 ∪ 𝐴 ∣ 𝐴 ⊂ Δ ∶ 𝑓𝑖𝑛𝑖𝑡𝑒 𝑚𝑢𝑙𝑡𝑖𝑠𝑒𝑡 }
の全体を渡る
Prop
(𝔅, 𝑑 𝐵) は距離空間 □

Hausdorff 距離
一方距離空間 𝑌, 𝑑 に対し
その部分集合の間に (Gromov-)Hausdorff 距離が定義される：
𝑑 𝐻 𝐴, 𝐵 ≔ max(sup
𝑎∈𝐴
𝑑 𝑎, 𝐵 , sup
𝑏∈𝐵
𝑑 𝑏, 𝐴 )
Bottleneck distance と pt cloud 間の Hausdorff 距離を比べたには次の不等式
がなり
Thm(Stability)
𝑋, 𝑋′: 𝑝𝑡 𝑐𝑙𝑜𝑢𝑑 とする。このとき
𝑑 𝐵 𝐵 𝑋 , 𝐵 𝑋′ ≤ 𝑑 𝐻(𝑋, 𝑋′)

Stability
barcode の間のBottleneck distance と pt cloud 間の Hausdorff 距離を比べる
と，その間には次の関係がある
Thm(Stability)
𝑋, 𝑋′: 𝑝𝑡 𝑐𝑙𝑜𝑢𝑑 とする。このとき
𝑑 𝐵 𝐵 𝑋 , 𝐵 𝑋′ ≤ 𝑑 𝐻(𝑋, 𝑋′)
特に bar-code をとる操作は Lipschitz 連続 □

Introduction to Persistence Theory

More Related Content

Introduction to Persistence Theory

Editor's Notes