「内積が見えると統計学も見える」第5回 プログラマのための数学勉強会 発表資料
•
266 likes•97,856 views
「第5回 プログラマのための数学勉強会 発表資料 (2015/11/21[sat])」 内容は統計学の素養がある方には基本的な事項ですが、ベクトルと内積で見方を変えてみたという点と、あまり統計学に親しみがない方にも理解してもらえるようなまとめになっている、というところに本スライドの独自性があると考えていますので、その辺り良ければご覧ください＾＾
「内積が見えると統計学も見える」第5回 プログラマのための数学勉強会 発表資料
- 1. 線形代数が見えると 統計学も見える 内積 2015/11/21 第5回 プログラマのための数学勉強会 発表資料 Ken ichi Matsui (@kenmatsu4)
- 2. 自己紹介: @kenmatsu4 ・Facebookページ https://www.facebook.com/matsukenbook ・Twitterアカウント @kenmatsu4 ・Qiitaでブログを書いています（統計、機械学習、Python等） http://qiita.com/kenmatsu4 （4100 contributionを超えました！） ・趣味 - バンドでベースを弾いたりしています。 - 主に東南アジアへバックパック旅行に行ったりします （カンボジア、ミャンマー、バングラデシュ、新疆ウイグル自治区 etc） 旅行の写真 : http://matsu-ken.jimdo.com Twitterアイコン
- 8. MASAKARI Come On! щ(゜ロ゜щ) みんなで勉強しましょう https://twitter.com/_inundata/status/616658949761302528
- 9. まずは、内積の話から。
- 10. とすると、内積とは ベクトル を n次元ベクトル 定義 1 a = (a1, a2, · · · , an)T , b = (b1, b2, · · · , bn)T a, b a · b = a1b1 + · · · + anbn = nX i=1 aibi a b
- 11. とすると、内積とは ベクトル を n次元ベクトル 定義 1 a = (a1, a2, · · · , an)T , b = (b1, b2, · · · , bn)T a, b a · b = a1b1 + · · · + anbn = nX i=1 aibi n n 1 1 ・ a b ベクトルからスカラに変換する 何らかの掛け算的な操作であることは わかるが、それ以上よくわからない
- 12. ベクトル a = (a1, a2, · · · , an)T , の長さ(ノルム)は、 のように、自身との内積のルートとして 表せます a kak2 kak = p a1 · a1 + · · · + an · an = v u u t nX i=1 a2 i = p a · a
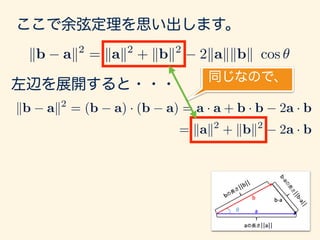
- 13. ここで余弦定理を思い出します。 kb ak2 = kak2 + kbk2 2kakkbk cos ✓
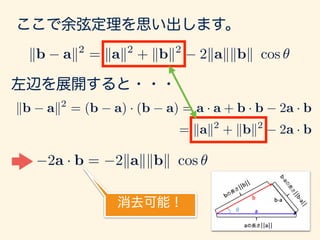
- 14. ここで余弦定理を思い出します。 kb ak2 = kak2 + kbk2 2kakkbk cos ✓ kb ak2 = (b a) · (b a) = a · a + b · b 2a · b = kak2 + kbk2 2a · b 左辺を展開すると・・・
- 15. ここで余弦定理を思い出します。 kb ak2 = kak2 + kbk2 2kakkbk cos ✓ kb ak2 = (b a) · (b a) = a · a + b · b 2a · b = kak2 + kbk2 2a · b 左辺を展開すると・・・ 同じなので、
- 16. ここで余弦定理を思い出します。 kb ak2 = kak2 + kbk2 2kakkbk cos ✓ kb ak2 = (b a) · (b a) = a · a + b · b 2a · b = kak2 + kbk2 2a · b 左辺を展開すると・・・ 消去可能！ 2a · b = 2kakkbk cos ✓ ) a · b = kakkbk cos ✓
- 17. ここで余弦定理を思い出します。 kb ak2 = kak2 + kbk2 2kakkbk cos ✓ kb ak2 = (b a) · (b a) = a · a + b · b 2a · b = kak2 + kbk2 2a · b 左辺を展開すると・・・ 2a · b = 2kakkbk cos ✓ ) a · b = kakkbk cos ✓ a · b = kakkbk cos ✓
- 18. a · b = kakkbk cos ✓ 定義２ よって、もう一つの内積の定義、 と同値であることがわかりました。
- 20. a · b = kakkbk cos ✓ をもうちょっと見える形で考えます。
- 21. cos ✓ = kck krk cosθの定義は です。
- 22. ) krk cos ✓ = kck cos ✓ = kck krk と、変形できるので、 ¦¦c¦¦は半径の長さにcosθをかけたもの と理解できます。
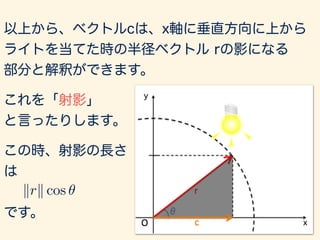
- 23. 以上から、ベクトルcは、x軸に垂直方向に上から ライトを当てた時の半径ベクトル rの影になる 部分と解釈ができます。 これを「射影」 と言ったりします。 この時、射影の長さ は です。 ) krk cos ✓ = kck
- 24. a · b = kakkbk cos ✓ 以上の議論をふまえて、内積を理解する ベクトル の長さc ベクトル の長さa a b θ c = kbk cos ✓
- 25. a b θ c = kbk cos ✓ 以上の議論をふまえて、内積を理解する a · b = kakkbk cos ✓ ベクトル の長さc ベクトル の長さ つまり、同じ方向を向く 成分にあわせてあげて、 その方向の長さを 掛け算したもの！ a
- 26. a b θ c = kbk cos ✓ この絵の場合、aの方向にあわせている 以上の議論をふまえて、内積を理解する a · b = kakkbk cos ✓ ベクトル の長さc ベクトル の長さa つまり、同じ方向を向く 成分にあわせてあげて、 その方向の長さを 掛け算したもの！
- 27. なので、角度が垂直だと、射影した の長さ が0になってしまうので、内積も 0 になる。 c 逆も然り。 内積が０だと垂直と言える。
- 28. ２つのベクトル , の 長さが１だった場合 a b
- 29. a · b = kakkbk cos ✓ = cos ✓ = 1 = 1
- 30. a · b = kakkbk cos ✓ = cos ✓ = 1 = 1 内積はcosθ となる。
- 31. この節のまとめ
- 32. この節のまとめ a · b = a1b1 + · · · + anbn = nX i=1 aibi a · b = kakkbk cos ✓ a b θ c = kbk cos ✓ 内積には２つの定義があり、 射影される側のベクトルの長さが1の時は、内積は cosθである。 計算するならこちら 意味がわかるのはこちら
- 33. ここで次に統計学の話を
- 36. carsデータセット (speedデータ) = ¯x = 1 n nX i=1 xi平均 = s2 = 1 n nX i=1 (xi ¯x)2 分散 標準偏差 = s = v u u t 1 n nX i=1 (xi ¯x)2 偏差
- 37. 標準偏差 = s = v u u t 1 n nX i=1 (xi ¯x)2 carsデータセット (speedデータ) = ¯x = 1 n nX i=1 xi平均 = s2 = 1 n nX i=1 (xi ¯x)2 分散 各データ平均からの差をそ れぞれ２乗して和をとった もの。散らばり具合の指標 偏差
- 38. 分散・標準偏差の視覚的イメージ 2 = s2 = 1 n nX i=1 (xi ¯x)2 偏差は、単純に足し てしまうと、釣り合っ ているので0になる → 偏差2乗しているオレンジの正方形の面積を平均した もの。下記では中心をずらしているが、最小となるのが 平均( )の位置¯x 2乗する https://goo.gl/6DROOA アニメーション：
- 39. 分散・標準偏差の視覚的イメージ 分散のままだと、単位が面積になので元のデータの単位 と合わない。なので、ルートをとって元の単位に戻した ものが標準偏差。 = s = v u u t 1 n nX i=1 (xi ¯x)2
- 40. 分散・標準偏差のもう一つのイメージ x = (x1, · · · , xn) x0 = (x1 ¯x, · · · , xn ¯x) データをn次元ベクトル として見てみる。x 平均 からの偏差のベクトルを¯x とすると、その時、 の長さ はx0 kx0 k kx0 k = v u u t nX i=1 (xi ¯x)2 で、表される。
- 41. 分散・標準偏差のもう一つのイメージ よって = s = v u u t 1 n nX i=1 (xi ¯x)2 = r 1 n v u u t nX i=1 (xi ¯x)2 = r 1 n kx0 k となり、標準偏差はベクトル の長さの 一種と考えられる。 x0 kx0 k = v u u t nX i=1 (xi ¯x)2 x’ kx 0 k
- 42. ちなみに、 Ex: 偏差値 名前 数学 偏差 標準偏差 何個分？ ← 10倍 ← + 50 田中 96 15 1.27 12.74 62.74 高橋 63 -18 -1.53 -15.29 34.71 鈴木 85 4 0.34 3.40 53.40 渡辺 66 -15 -1.27 -12.74 37.26 清水 91 10 0.85 8.50 58.50 木村 89 8 0.68 6.80 56.80 山本 77 -4 -0.34 -3.40 46.60 平均 81.00 標準偏差 11.77 これが「偏差値」
- 43. この節のまとめ
- 44. この節のまとめ データをn次元上の１本のベクトル として見てみる。 また、平均からの偏差ベクトルを下記のように定義した x s = r 1 n v u u t nX i=1 (xi ¯x)2 = r 1 n kx0 k x0 = (x1 ¯x, · · · , xn ¯x) このようにすると標準偏差は、 のようにベクトルの長さの一種と捉えることができる。
- 45. 相関係数について
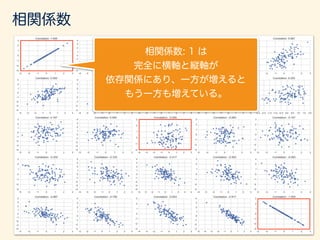
- 46. 相関係数 Xの値が増加すると、Yの値も増加する → 正の相関がある Xの値が増加すると、Yの値が減少する → 負の相関がある これを数値化したものに「相関係数」がある。 r = P (xi ¯x)(yi ¯y) pP (xi ¯x)2 pP (yi ¯y)2 相関係数 =
- 47. 相関係数
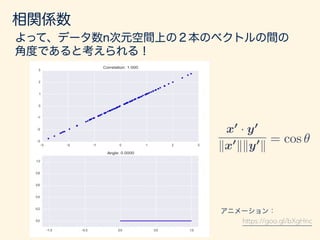
- 51. 相関係数 r = P (xi ¯x)(yi ¯y) pP (xi ¯x)2 pP (yi ¯y)2 相関係数 = 式をよく見てみると、 = x0 · y0 kx0 kky0 k あれ、これって？
- 52. 相関係数 r = P (xi ¯x)(yi ¯y) pP (xi ¯x)2 pP (yi ¯y)2 相関係数 = 式をよく見てみると、 = x0 · y0 kx0 kky0 k = cos ✓ 内積の定義から cosθだ！ あれ、これって？ θ x’ y’ データ数nのとき、n次元の 高次元空間の２本のベクトル と見なす(平均を引いて中心を揃えてあることに注意)
- 54. この節のまとめ
- 55. この節のまとめ r = P (xi ¯x)(yi ¯y) pP (xi ¯x)2 pP (yi ¯y)2 相関係数 = = x0 · y0 kx0 kky0 k = cos ✓ ２つのデータ間の相関関係を表す「相関係数」は データをベクトルとして捉えると、n次元空間上の ２本のベクトルの間の角度と捉えることができた。 θ x’ y’
- 56. 回帰分析について
- 57. 回帰分析 (単回帰分析) : carデータセット → スピードと距離の間に直線的な関係がありそうに みえる。 距離 = + スピード↵
- 58. → スピードと距離の間に直線的な関係がありそうに みえる。 回帰分析 一番良い線を選ぶ基準として 点と線の間の長さを全部足し 合わせたものを最小すること を考える。 残差 yi = ↵ + xi + ei これをiについて 和をとる
- 59. 回帰分析 yi = ↵ + xi + ei ei = yi (↵ + xi)→ min S(↵, ) = min nX i=1 e2 i = min nX i=1 {yi (↵ + xi)}2 よって、下記の最小化問題となる。(最小二乗法) ↵ + xi yi ei
- 60. 回帰分析 → 黒い線(残差)が最小になるようにα、βを調整する αを変えてみる βを変えてみる https://goo.gl/BDtIU0 https://goo.gl/jmrk07 アニメーション：アニメーション：
- 61. 回帰分析 @S(↵, ) @↵ = 0 @S(↵, ) @ = 0 を解くことで、Sが最小となる αとβを求められる。
- 62. 回帰分析 前ページの計算を解くと、 ˆ↵ = ¯y ˆ¯x となる。 ˆ = P (xi ¯x)(yi ¯y) P (xi ¯x)2
- 63. を深掘りしてみるˆ
- 64. 回帰分析 前述のように、偏差をプライムで表すと、 ˆ = P (xi ¯x)(yi ¯y) P (xi ¯x)2 = x0 · y0 kx0 k2 内積と、ベクトルの長さで 表現できる！
- 65. 回帰分析 ˆ = x0 · y0 kx0 k2 = x0 kx0 k2 · y0 この２つのベクトルの内積と 考えられる。 x’ y’ θ = x0 /kx0 k ˆ = 1 kx0k x0 kx0k · y0 長さ 1 はベクトルx’をかけると 射影と同じ長さのベクトル ˆx = ky0 k cos ✓/kx0 k x = ky0 k kx0k cos ✓ スカラ ベクトル
- 66. この節のまとめ
- 67. この節のまとめ 2つのデータの間に線形関係を当てはめてみる分析手法 yi = ↵ + xi + ei 上記のモデルに対して、残差eiを最小にするα、βを 最小二乗法で求めた。
- 68. 傾きに相当する はベクトル x’に掛けあわせると ベクトル y’ の射影の長さと同じベクトルになる、と 捉えることができた。 この節のまとめ x’ y’ θ = x0 /kx0 k ˆ ˆx = ky0 k cos ✓/kx0 k x スカラ ベクトル
- 69. 主成分分析について
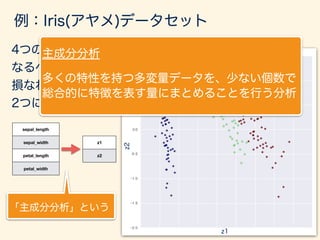
- 70. 例：Iris(アヤメ)データセット → データ分析界のHello World的なデータです ID sepal_length sepal_width petal_length petal_width target 0 5.1 3.5 1.4 0.2 0 1 4.9 3.0 1.4 0.2 0 2 4.7 3.2 1.3 0.2 0 3 4.6 3.1 1.5 0.2 0 4 5.0 3.6 1.4 0.2 0 5 5.4 3.9 1.7 0.4 0 6 4.6 3.4 1.4 0.3 0 7 5.0 3.4 1.5 0.2 0 8 4.4 2.9 1.4 0.2 0 9 4.9 3.1 1.5 0.1 0 … http://blog.kaggle.com/2015/04/22/scikit-learn-video-3-machine-learning-first-steps-with-the-iris-dataset/ アヤメの種別 0: setosa, 1: versicolor, 2: virginica 花弁 萼片
- 75. 主成分分析の仕組み (もう少し単純なデータで) ID Math Japanese 1 20 9 2 4 2 3 12 15 4 5 10 5 10 6 6 8 11 7 1 4 8 15 9 9 5 6 数学・国語の2教科の成績データから総合的な学力の 指標を算出してみます。 2次元データを1次元に落とす
- 78. xi = (xi1, xi2) 1 1 長さ: kxikcos✓θ z(1) a 内積！ 主成分としての１つ目の軸を とすると、 に対する 主成分は と表せる。 ( ) z(1) xi z(1)i = (a · xi)a 主成分分析の仕組み (2次元の例) = z(1)i = a · xi a = (a1, a2)T 情報損失量
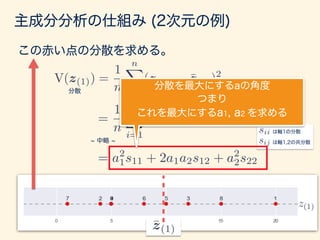
- 79. この赤い点の分散を求める。 主成分分析の仕組み (2次元の例) V(z(1)) = 1 n nX i=1 (z(1)i ¯z(1))2 分散 = 1 n nX i=1 {(a · xi) (a · ¯x)}2 中略 は軸1の分散 は軸1,2の共分散 sii sij ¯z(1) z(1) = a2 1s11 + 2a1a2s12 + a2 2s22
- 80. この赤い点の分散を求める。 主成分分析の仕組み (2次元の例) V(z(1)) = 1 n nX i=1 (z(1)i ¯z(1))2 分散 = 1 n nX i=1 {(a · xi) (a · ¯x)}2 中略 は軸1の分散 は軸1,2の共分散 sii sij ¯z(1) z(1) 分散を最大にするaの角度 つまり これを最大にするa1, a2 を求める = a2 1s11 + 2a1a2s12 + a2 2s22
- 81. 主成分分析の仕組み (2次元の例) = a2 i s11 + 2a1a2s12 + a2 2s22 ただし、 は、ベクトル が長くなればなるほど大きくなるので、 長さは１ a kak2 = 1 という制約をつける。 以上より・・・
- 82. 主成分分析の仕組み (2次元の例) 主成分分析は以下の条件つき最大化問題として解く。 s.t. kak2 = 1 max a2 1s11 + 2a1a2s12 + a2 2s22 条件つき最適化問題 「ラグランジュの未定乗数法」で解く
- 83. s.t. kak2 = 1 max a2 1s11 + 2a1a2s12 + a2 2s22 主成分分析の仕組み (2次元の例) F(a1, a2, ) = a2 1s11 + 2a1a2s12 + a2 2s22 (a2 1 + a2 2 1) @F @a1 = 2a1s11 + 2a2s12 2 a1 = 0 @F @a2 = 2a2s22 + 2a1s12 2 a2 = 0 @F @ = a2 1 + a2 2 1 = 0 微分して0と置く
- 84. 主成分分析の仕組み (2次元の例) 前ページの式を整理すると、 s11 s12 s12 s22 a1 a2 = a1 a2 分散共分散行列の固有値問題となっている！
- 85. 分散共分散行列の固有値問題？
- 86. (※ よりこれが言える) 分散共分散行列の固有値問題？ S = s11 s12 s12 s22 = 2.0 s12 s12 5.0 例) 分散が、横軸 2.0、縦軸 5.0の場合 また、分散と共分散の関係から、共分散の上下限は それぞれの標準偏差を掛けたものとなる。 |sij| p siisjj |a · b| = |kakkbk cos ✓| kakkbk 上記の数値例の場合、 上下限は 13.1622
- 87. 分散共分散行列の固有値問題？ 例) 分散が、横軸 2.0、縦軸 5.0の、共分散0の場合 S = s11 s12 s12 s22 = 2.0 0 0 5.0 (1, 0) (0, 1) (2, 0) (0, 5)
- 88. 分散共分散行列の固有値問題？ 例) 分散が、横軸 2.0、縦軸 5.0の、共分散1.0の場合 (1, 0) (0, 1) (2, 1) (1, 5) S = s11 s12 s12 s22 = 2.0 1.0 1.0 5.0
- 93. 主成分分析の仕組み (2次元の例) ベクトル a の向きが決まったので、その軸上にデータ を落として指標としたり、分類を実行したりする。
- 94. この節のまとめ
- 95. この節のまとめ 次元を削減する手法の１つとして主成分分析を紹介し、 その求め方には、内積を理解すると何をしている処理 であるか、イメージをつけやすいことを説明した。 ID sepal_length sepal_width petal_length petal_width target 0 5.1 3.5 1.4 0.2 0 1 4.9 3.0 1.4 0.2 0 2 4.7 3.2 1.3 0.2 0 3 4.6 3.1 1.5 0.2 0 4 5.0 3.6 1.4 0.2 0 5 5.4 3.9 1.7 0.4 0 4次元から 2次元へ
- 96. 参考 ・【統計学】初めての「標準偏差」（統計学に挫折しないために） (Qiita) http://qiita.com/kenmatsu4/items/e6c6acb289c02609e619 ・【数学】固有値・固有ベクトルとは何かを可視化してみる(Qiita) http://qiita.com/kenmatsu4/items/2a8573e3c878fc2da306 ・主成分分析 http://www.e.okayama-u.ac.jp/ nagahata/bstat/rta5syo.pdf ・今日のPythonコード on GitHub https://github.com/matsuken92/Qiita_Contents/blob/master/ math_for_programmer/demo_math_stats_004.ipynb