Axioms

16 pages, 37098 KiB

Open AccessFeature PaperArticle

On Analytical Continuation of the Horn’s Hypergeometric Functions H₃ and Their Ratios

by Roman Dmytryshyn, Tamara Antonova and Sofiia Hladun

Axioms 2025, 14(1), 67; https://doi.org/10.3390/axioms14010067 - 16 Jan 2025

This paper considers the Horn’s hypergeometric function

H_{3}

, which is closely related to other hypergeometric functions and has various mathematical or physical applications. The problem of analytical extension of this function is solved using a special family of functions—branched continued fractions. [...] Read more.

This paper considers the Horn’s hypergeometric function

H_{3}

, which is closely related to other hypergeometric functions and has various mathematical or physical applications. The problem of analytical extension of this function is solved using a special family of functions—branched continued fractions. A new domain of analytical extension of the Horn’s hypergeometric functions

H_{3}

and their ratios under certain conditions to real parameters are established. This paper also contains an example of the presentation and continuation of some special function and an analysis of numerical results. Full article

(This article belongs to the Section Mathematical Analysis)

► Show Figures

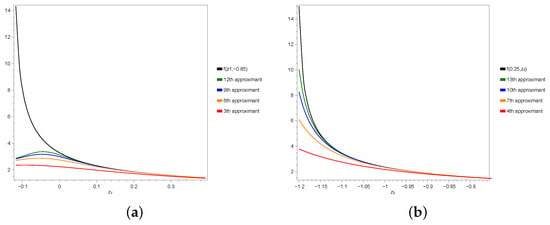
Figure 1

11 pages, 286 KiB

Open AccessArticle

Vector Meson Spectrum from Top-Down Holographic QCD

by Mohammed Mia, Keshav Dasgupta, Charles Gale, Michael Richard and Olivier Trottier

Axioms 2025, 14(1), 66; https://doi.org/10.3390/axioms14010066 - 16 Jan 2025

Abstract

We elaborate on the brane configuration that gives rise to a QCD-like gauge theory that confines at low energies and becomes scale invariant at the highest energies. In the limit where the rank of the gauge group is large, a gravitational description emerges. [...] Read more.

We elaborate on the brane configuration that gives rise to a QCD-like gauge theory that confines at low energies and becomes scale invariant at the highest energies. In the limit where the rank of the gauge group is large, a gravitational description emerges. For the confined phase, we obtain a vector meson spectrum and demonstrate how a certain choice of parameters can lead to quantitative agreement with empirical data. Full article

(This article belongs to the Special Issue Mathematical Aspects of Quantum Field Theory and Quantization)

► Show Figures

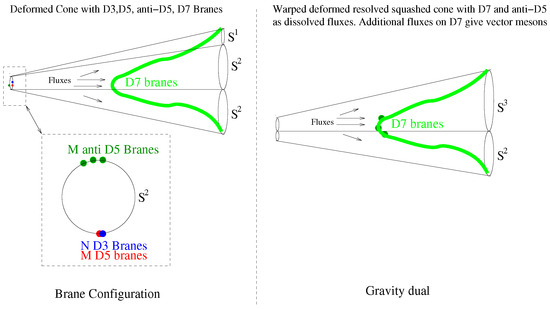
Figure 1

33 pages, 737 KiB

Open AccessFeature PaperArticle

Orthogonal Polynomials on Radial Rays in the Complex Plane: Construction, Properties and Applications

by Gradimir V. Milovanović

Axioms 2025, 14(1), 65; https://doi.org/10.3390/axioms14010065 - 16 Jan 2025

Abstract

Orthogonal polynomials on radial rays in the complex plane were introduced and studied intensively in several papers almost three decades ago. This paper presents an account of such kinds of orthogonality in the complex plane, as well as a number of new results [...] Read more.

Orthogonal polynomials on radial rays in the complex plane were introduced and studied intensively in several papers almost three decades ago. This paper presents an account of such kinds of orthogonality in the complex plane, as well as a number of new results and examples. In addition to several types of standard orthogonality, the concept of orthogonality on arbitrary radial rays is introduced, some or all of which may be infinite. A general method for numerical constructing, the so-called discretized Stieltjes–Gautschi procedure, is described and several interesting examples are presented. The main properties, zero distribution and some applications are also given. Special attention is paid to completely symmetric cases. Recurrence relations for such kinds of orthogonal polynomials and their zero distribution, as well as a connection with the standard polynomials orthogonal on the real line, are derived, including the corresponding linear differential equation of the second order. Finally, some applications in physics and electrostatics are mentioned. Full article

(This article belongs to the Special Issue Orthogonal Polynomials, Special Functions and Applications: 2nd Edition)

► Show Figures

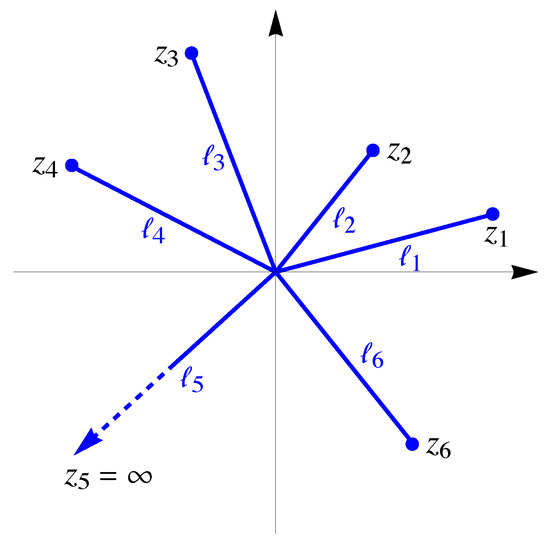
Figure 1

17 pages, 269 KiB

Open AccessArticle

Twofold Auxiliary Information Under Two-Phase Sampling: An Improved Family of Double-Transformed Variance Estimators

by Umer Daraz, Della Agustiana, Jinbiao Wu and Walid Emam

Axioms 2025, 14(1), 64; https://doi.org/10.3390/axioms14010064 - 16 Jan 2025

Abstract

Outlier values and rankings are important for emphasizing data distribution variability, which improves the accuracy and effectiveness of variance estimations. To enhance the estimation of finite population variance in a two-phase sampling framework, this study presents an improved class of double exponential-type estimators [...] Read more.

Outlier values and rankings are important for emphasizing data distribution variability, which improves the accuracy and effectiveness of variance estimations. To enhance the estimation of finite population variance in a two-phase sampling framework, this study presents an improved class of double exponential-type estimators by utilizing the outlier values and ranks of an auxiliary variable. A theoretical analysis is conducted to derive the biases and mean squared errors (MSEs) of these estimators using first-order approximations. A comprehensive simulation study is then performed to analyze the performance of the proposed estimators. The results clearly show that the new estimators provide more precise estimates, achieving a higher percentage relative efficiency (PRE) across all simulated scenarios. Furthermore, three data sets are analyzed to further confirm the efficiency of the proposed estimators as compared to other existing estimators. These results emphasize the potential of the proposed class of estimators to optimize variance estimation techniques, making it a more cost-effective and accurate choice for researchers using two-phase sampling in a variety of domains. Full article

33 pages, 3898 KiB

Open AccessArticle

Effects of Predation-Induced Emigration on a Landscape Ecological Model

by James T. Cronin, Nalin Fonseka, Jerome Goddard II, Ratnasingham Shivaji and Xiaohuan Xue

Axioms 2025, 14(1), 63; https://doi.org/10.3390/axioms14010063 - 16 Jan 2025

Abstract

Predators impact prey populations directly through consumption and indirectly via trait-mediated effects like predator-induced emigration (PIE), where prey alter movement due to predation risk. While PIE can significantly influence prey dynamics, its combined effect with direct predation in fragmented habitats is underexplored. Habitat [...] Read more.

Predators impact prey populations directly through consumption and indirectly via trait-mediated effects like predator-induced emigration (PIE), where prey alter movement due to predation risk. While PIE can significantly influence prey dynamics, its combined effect with direct predation in fragmented habitats is underexplored. Habitat fragmentation reduces viable habitats and isolates populations, necessitating an understanding of these interactions for conservation. In this paper, we present a reaction–diffusion model to investigate prey persistence under both direct predation and PIE in fragmented landscapes. The model considers prey growing logistically within a bounded habitat patch surrounded by a hostile matrix. Prey move via unbiased random walks internally but exhibit biased movement at habitat boundaries influenced by predation risk. Predators are assumed constant, operating on a different timescale. We examine three predation functional responses—constant yield, Holling Type I, and Holling Type III—and three emigration patterns: density-independent, positive density-dependent, and negative density-dependent emigration. Using the method of sub- and supersolutions, we establish conditions for the existence and multiplicity of positive steady-state solutions. Numerical simulations in one-dimensional habitats further elucidate the structure of these solutions. Our findings demonstrate that the interplay between direct predation and PIE crucially affects prey persistence in fragmented habitats. Depending on the functional response and emigration pattern, PIE can either mitigate or amplify the impact of direct predation. This underscores the importance of incorporating both direct and indirect predation effects in ecological models to better predict species dynamics and inform conservation strategies in fragmented landscapes. Full article

► Show Figures

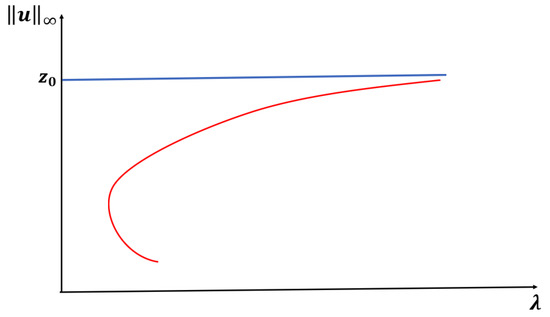
Figure 1

12 pages, 267 KiB

Open AccessArticle

An Improvement of the Lower Bound on the Maximum Number of Halving Lines for Sets in the Plane with an Odd Number of Points

by Javier Rodrigo, Mariló López, Danilo Magistrali and Estrella Alonso

Axioms 2025, 14(1), 62; https://doi.org/10.3390/axioms14010062 - 16 Jan 2025

Abstract

In this paper, we give examples that improve the lower bound on the maximum number of halving lines for sets in the plane with 35, 59, 95, and 97 points and, as a consequence, we improve the current best upper bound of the [...] Read more.

In this paper, we give examples that improve the lower bound on the maximum number of halving lines for sets in the plane with 35, 59, 95, and 97 points and, as a consequence, we improve the current best upper bound of the rectilinear crossing number for sets in the plane with 35, 59, 95, and 97 points, provided that a conjecture included in the literature is true. As another consequence, we also improve the lower bound on the maximum number of halving pseudolines for sets in the plane with 35 points. These examples, and the recursive bounds for the maximum number of halving lines for sets with an odd number of points achieved, give a new insight in the study of the rectilinear crossing number problem, one of the most challenging tasks in Discrete Geometry. With respect to this problem, it is conjectured that, for all n multiples of 3, there are 3-symmetric sets of n points for which the rectilinear crossing number is attained. Full article

(This article belongs to the Special Issue Trends in Differential Geometry and Algebraic Topology)

► Show Figures

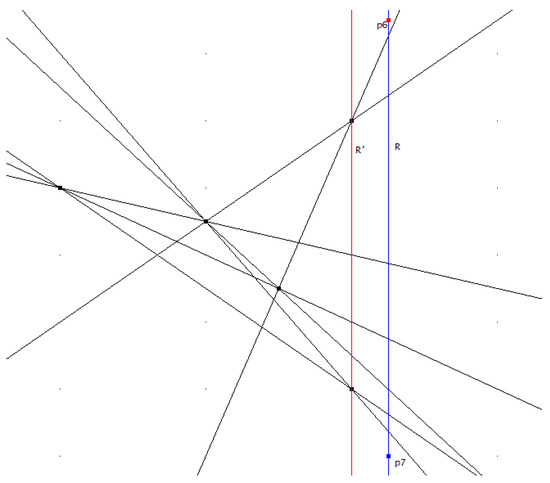
Figure 1

16 pages, 295 KiB

Open AccessFeature PaperArticle

Homogeneous Structures and Homogeneous Geodesics of the Hyperbolic Oscillator Group

by Giovanni Calvaruso, Amirhesam Zaeim, Mehdi Jafari and Moslem Baghgoli

Axioms 2025, 14(1), 61; https://doi.org/10.3390/axioms14010061 - 15 Jan 2025

Abstract

In this paper, we study some homogeneity properties of a semi-direct extension of the Heisenberg group, known in literature as the hyperbolic oscillator (or Boidol) group, equipped with the left-invariant metrics corresponding to the ones of the oscillator group. We identify the naturally [...] Read more.

In this paper, we study some homogeneity properties of a semi-direct extension of the Heisenberg group, known in literature as the hyperbolic oscillator (or Boidol) group, equipped with the left-invariant metrics corresponding to the ones of the oscillator group. We identify the naturally reductive case by the existence of the corresponding special homogeneous structures. For the cases where these special homogeneous structures do not exist, we exhibit a complete description of the homogeneous geodesics. Full article

(This article belongs to the Section Geometry and Topology)

30 pages, 651 KiB

Open AccessArticle

Modified Heisenberg Commutation Relations, Free Schrödinger Equations, Tunnel Effect and Its Connections with the Black–Scholes Equation

by Mauricio Contreras González, Roberto Ortiz Herrera and José González Suárez

Axioms 2025, 14(1), 60; https://doi.org/10.3390/axioms14010060 - 15 Jan 2025

Abstract

This paper explores the implications of modifying the canonical Heisenberg commutation relations over two simple systems, such as the free particle and the tunnel effect generated by a step-like potential. The modified commutation relations include position-dependent and momentum-dependent terms analyzed separately. For the [...] Read more.

This paper explores the implications of modifying the canonical Heisenberg commutation relations over two simple systems, such as the free particle and the tunnel effect generated by a step-like potential. The modified commutation relations include position-dependent and momentum-dependent terms analyzed separately. For the position deformation case, the corresponding free wave functions are sinusoidal functions with a variable wave vector

k (x)

. In the momentum deformation case, the wave function has the usual sinusoidal behavior, but the energy spectrum becomes non-symmetric in terms of momentum. Tunneling probabilities depend on the deformation strength for both cases. Also, surprisingly, the quantum mechanical model generated by these modified commutation relations is related to the Black–Scholes model in finance. In fact, by taking a particular form of a linear position deformation, one can derive a Black–Scholes equation for the wave function when an external electromagnetic potential is acting on the particle. In this way, the Scholes model can be interpreted as a quantum-deformed model. Furthermore, by identifying the position coordinate x in quantum mechanics with the underlying asset S, which in finance satisfies stochastic dynamics, this analogy implies that the Black–Scholes equation becomes a quantum mechanical system defined over a random spatial geometry. If the spatial coordinate oscillates randomly about its mean value, the quantum particle’s mass would correspond to the inverse of the variance of this stochastic coordinate. Further, because this random geometry is nothing more than gravity at the microscopic level, the Black–Scholes equation becomes a possible simple model for understanding quantum gravity. Full article

(This article belongs to the Section Mathematical Physics)

► Show Figures

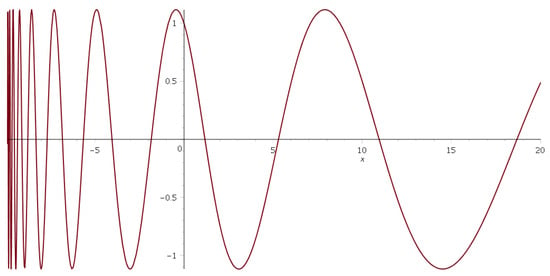
Figure 1

14 pages, 290 KiB

Open AccessArticle

Approximation and the Multidimensional Moment Problem

by Octav Olteanu

Axioms 2025, 14(1), 59; https://doi.org/10.3390/axioms14010059 - 14 Jan 2025

Abstract

The aim of this paper is to apply polynomial approximation by sums of squares in several real variables to the multidimensional moment problem. The general idea is to approximate any element of the positive cone of the involved function space with sums whose [...] Read more.

The aim of this paper is to apply polynomial approximation by sums of squares in several real variables to the multidimensional moment problem. The general idea is to approximate any element of the positive cone of the involved function space with sums whose terms are squares of polynomials. First, approximations on a Cartesian product of intervals by polynomials taking nonnegative values on the entire

R^{2}

, or on

R_{+}^{2}

, are considered. Such results are discussed in

L_{μ}^{1} (R^{2})

and in

C (S_{1} \times S_{2})

-type spaces, for a large class of measures,

μ,

for compact subsets

S_{i}, i = 1, 2

of the interval

[0, + \infty)

. Thus, on such subsets, any nonnegative function is a limit of sums of squares. Secondly, applications to the bidimensional moment problem are derived in terms of quadratic expressions. As is well known, in multidimensional cases, such results are difficult to prove. Directions for future work are also outlined. Full article

(This article belongs to the Special Issue Numerical Methods and Approximation Theory)

27 pages, 360 KiB

Open AccessArticle

Interior Peak Solutions for a Semilinear Dirichlet Problem

by Hissah Alharbi, Hibah Alkhuzayyim, Mohamed Ben Ayed and Khalil El Mehdi

Axioms 2025, 14(1), 58; https://doi.org/10.3390/axioms14010058 - 13 Jan 2025

Abstract

In this paper, we consider the semilinear Dirichlet problem

(P_{ε}) : - Δ u + V (x) u = u^{\frac{n + 2}{n - 2} - ε}

,

u > 0

in ,

u = 0

on [...] Read more.

In this paper, we consider the semilinear Dirichlet problem

(P_{ε}) : - Δ u + V (x) u = u^{\frac{n + 2}{n - 2} - ε}

,

u > 0

in ,

u = 0

on ∂, where is a bounded regular domain in

R^{n}

,

n \geq 4

,

ε

is a small positive parameter, and V is a non-constant positive

C^{2}

-function on

\bar{Ω}

. We construct interior peak solutions with isolated bubbles. This leads to a multiplicity result for

(P_{ε})

. The proof of our results relies on precise expansions of the gradient of the Euler–Lagrange functional associated with

(P_{ε})

, along with a suitable projection of the bubbles. This projection and its associated estimates are new and play a crucial role in tackling such types of problems. Full article

19 pages, 294 KiB

Open AccessArticle

Quantum–Fractal–Fractional Operator in a Complex Domain

by Adel A. Attiya, Rabha W. Ibrahim, Ali H. Hakami, Nak Eun Cho and Mansour F. Yassen

Axioms 2025, 14(1), 57; https://doi.org/10.3390/axioms14010057 - 13 Jan 2025

Abstract

In this effort, we extend the fractal–fractional operators into the complex plane together with the quantum calculus derivative to obtain a quantum–fractal–fractional operators (QFFOs). Using this newly created operator, we create an entirely novel subclass of analytical functions in the unit disk. Motivated [...] Read more.

In this effort, we extend the fractal–fractional operators into the complex plane together with the quantum calculus derivative to obtain a quantum–fractal–fractional operators (QFFOs). Using this newly created operator, we create an entirely novel subclass of analytical functions in the unit disk. Motivated by the concept of differential subordination, we explore the most important geometric properties of this novel operator. This leads to a study on a set of differential inequalities in the open unit disk. We focus on the conditions to obtain a bounded turning function of QFFOs. Some examples are considered, involving special functions like Bessel and generalized hypergeometric functions. Full article

(This article belongs to the Special Issue Recent Advances in Functional Analysis and Operator Theory)

28 pages, 399 KiB

Open AccessArticle

On the Work of Cartan and Münzner on Isoparametric Hypersurfaces

by Thomas E. Cecil and Patrick J. Ryan

Axioms 2025, 14(1), 56; https://doi.org/10.3390/axioms14010056 - 13 Jan 2025

Abstract

A hypersurface

M^{n}

in a real space form

R^{n + 1}

,

S^{n + 1}

, or

H^{n + 1}

is isoparametric if it has constant principal curvatures. This paper is a survey of the fundamental work of Cartan [...] Read more.

A hypersurface

M^{n}

in a real space form

R^{n + 1}

,

S^{n + 1}

, or

H^{n + 1}

is isoparametric if it has constant principal curvatures. This paper is a survey of the fundamental work of Cartan and Münzner on the theory of isoparametric hypersurfaces in real space forms, in particular, spheres. This work is contained in four papers of Cartan published during the period 1938–1940 and two papers of Münzner that were published in preprint form in the early 1970s and as journal articles in 1980–1981. These papers of Cartan and Münzner have been the foundation of the extensive field of isoparametric hypersurfaces, and they have all been recently translated into English by T. Cecil. The paper concludes with a brief survey of the recently completed classification of isoparametric hypersurfaces in spheres. Full article

(This article belongs to the Special Issue Advances in Differential Geometry and Singularity Theory, 2nd Edition)

12 pages, 261 KiB

Open AccessArticle

On the Asymptotic Expansions of the (p,k)-Analogues of the Gamma Function and Associated Functions

by Tomislav Burić

Axioms 2025, 14(1), 55; https://doi.org/10.3390/axioms14010055 - 13 Jan 2025

Abstract

General asymptotic expansion of the

(p, k)

-gamma function is obtained and various approaches to this expansion are studied. The numerical precision of the derived asymptotic formulas is shown and compared. Results are applied to the analogues of digamma and [...] Read more.

General asymptotic expansion of the

(p, k)

-gamma function is obtained and various approaches to this expansion are studied. The numerical precision of the derived asymptotic formulas is shown and compared. Results are applied to the analogues of digamma and polygamma functions, and asymptotic expansion of the quotient of two

(p, k)

-gamma functions is also derived and analyzed. Various examples and application to the k-Pochhammer symbol are presented. Full article

(This article belongs to the Special Issue Special Functions and Related Topics)

30 pages, 775 KiB

Open AccessArticle

Goodness-of-Fit Test for the Bivariate Negative Binomial Distribution

by Francisco Novoa-Muñoz and Juan Pablo Aguirre-González

Axioms 2025, 14(1), 54; https://doi.org/10.3390/axioms14010054 - 12 Jan 2025

Abstract

When modeling real-world data, we face the challenge of determining which probability distribution best represents the data. To address this intricate problem, we rely on goodness-of-fit tests. However, when the data come from a bivariate negative binomial distribution, the literature reveals no existing [...] Read more.

When modeling real-world data, we face the challenge of determining which probability distribution best represents the data. To address this intricate problem, we rely on goodness-of-fit tests. However, when the data come from a bivariate negative binomial distribution, the literature reveals no existing goodness-of-fit test for this distribution. For this reason, in this article, we propose and study a computationally convenient goodness-of-fit test for the bivariate negative binomial distribution. This test is based on a bootstrap approximation and a parallelization strategy. To this end, we use a reparameterization technique based on the probability generating function and a Cramér-von Mises-type statistic. From the simulation studies, we conclude that the results converge to the established nominal levels as the sample size increases, and in all cases considered, the parametric bootstrap method provides an accurate approximation of the null distribution of the statistic we propose. Additionally, we verify the power of the proposed test, as well as its application to five real datasets. To accelerate the massive computational work, we employ the parallelization strategy that, according to Novoa-Muñoz (2024), was the most efficient among the techniques he analyzed. Full article

(This article belongs to the Special Issue Advances in Statistical Simulation and Computing)

► Show Figures

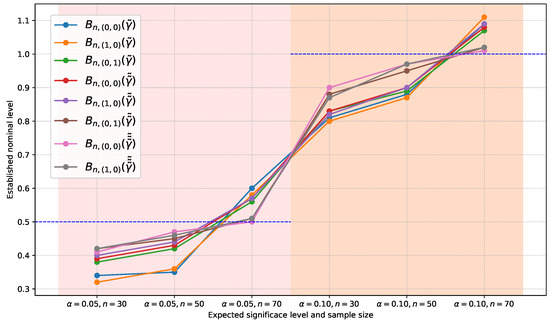
Figure A1

16 pages, 1861 KiB

Open AccessArticle

Dynamics of a Fractional-Order Eco-Epidemiological Model with Two Disease Strains in a Predator Population Incorporating Harvesting

by Moustafa El-Shahed and Mahmoud Moustafa

Axioms 2025, 14(1), 53; https://doi.org/10.3390/axioms14010053 - 11 Jan 2025

Abstract

In this paper, a fractional-order eco-epidemiological model with two disease strains in the predator population incorporating harvesting is formulated and analyzed. The model assumes that the population is divided into a prey population, a susceptible predator population, a predator population infected by the [...] Read more.

In this paper, a fractional-order eco-epidemiological model with two disease strains in the predator population incorporating harvesting is formulated and analyzed. The model assumes that the population is divided into a prey population, a susceptible predator population, a predator population infected by the first disease, and a predator population infected by the second disease. A mathematical analysis and numerical simulations are performed to explain the dynamics and properties of the proposed fractional-order eco-epidemiological model. The positivity, boundedness, existence, and uniqueness of the solutions are examined. The basic reproduction number and some sufficient conditions for the existence of four equilibrium points are obtained. In addition, some sufficient conditions are proposed to ensure the local and global asymptotic stability of the equilibrium points. Theoretical results are illustrated through numerical simulations, which also highlight the effect of the fractional order. Full article

(This article belongs to the Special Issue Advances in Dynamical Systems and Control)

► Show Figures

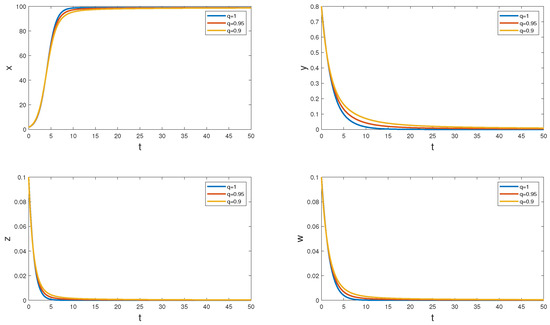
Figure 1

26 pages, 4050 KiB

Open AccessSystematic Review

A Systematic Overview of Fuzzy-Random Option Pricing in Discrete Time and Fuzzy-Random Binomial Extension Sensitive Interest Rate Pricing

by Jorge de Andrés-Sánchez

Axioms 2025, 14(1), 52; https://doi.org/10.3390/axioms14010052 - 10 Jan 2025

Abstract

Since the early 2000s, fuzzy mathematics has fostered a stream of research on the financial valuation of assets incorporating optionality. This paper makes two contributions to this field. First, it conducts a bibliographical analysis of contributions from fuzzy set theory to option pricing, [...] Read more.

Since the early 2000s, fuzzy mathematics has fostered a stream of research on the financial valuation of assets incorporating optionality. This paper makes two contributions to this field. First, it conducts a bibliographical analysis of contributions from fuzzy set theory to option pricing, focusing on fuzzy-random option pricing (FROP) and its applications in binomial and trinomial lattice approaches. Second, it extends the FROP to yield curve modeling within a binomial framework. The bibliographical analysis followed the PRISMA guidelines and was conducted via the SCOPUS and WoS databases. We present a structured review of papers on FROP in discrete time (FROPDT), identifying the principal papers and outlets. The findings reveal that this focus has been applied to price options on stocks, stock indices, and real options. However, the exploration of its application to the term structure of interest-sensitive interest rate assets is very rare. To address this gap, we develop a fuzzy-random extension of the Ho–Lee term structure model, applying it to the European interbank market and price caplet options. Full article

(This article belongs to the Special Issue New Perspectives in Fuzzy Sets and Their Applications, 2nd Edition)

► Show Figures

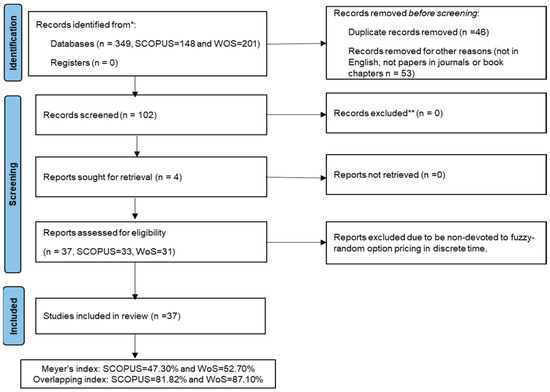
Figure 1

14 pages, 484 KiB

Open AccessArticle

The Axiomatic Characterization of the Grey Shapley Value

by Mehmet Gençtürk, Mahmut Sami Öztürk and Osman Palancı

Axioms 2025, 14(1), 51; https://doi.org/10.3390/axioms14010051 - 10 Jan 2025

Abstract

One of the most significant solution concepts in cooperative grey game theory is the grey Shapley value. This value is a fascinating one among the models and methods of operations research, and has been the subject of extensive study by other researchers. The [...] Read more.

One of the most significant solution concepts in cooperative grey game theory is the grey Shapley value. This value is a fascinating one among the models and methods of operations research, and has been the subject of extensive study by other researchers. The objective of this study is to characterize and redefine this value in cooperative games where coalition values are grey numbers. In this study, the grey Shapley value is characterized by the following axioms:

G

-gain loss,

G

-null player, and

G

-differential marginality. Finally, this study concludes with an investigation of some applications involving production costs. This study is based on an investigation of the costs incurred when milk producers collaborate. Full article

► Show Figures

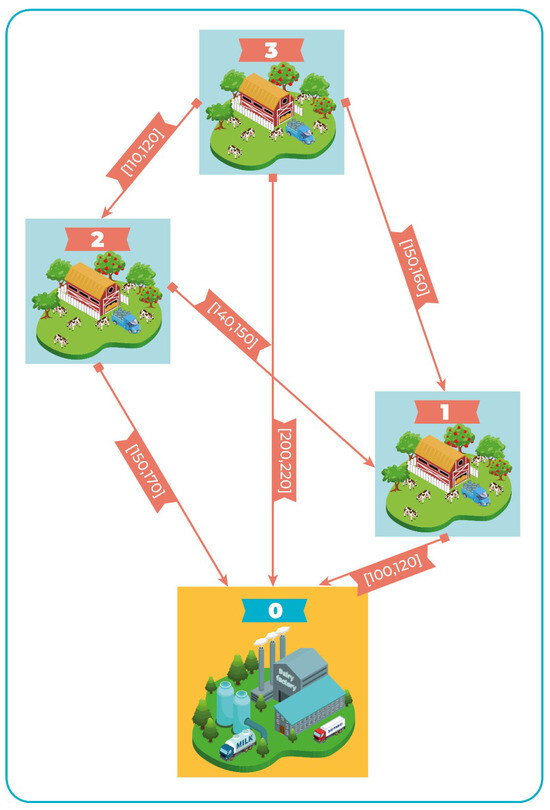
Figure 1

9 pages, 280 KiB

Open AccessArticle

Applications of Lucas Balancing Polynomial to Subclasses of Bi-Starlike Functions

by Gangadharan Murugusundaramoorthy, Luminita-Ioana Cotîrlă, Daniel Breaz and Sheza M. El-Deeb

Axioms 2025, 14(1), 50; https://doi.org/10.3390/axioms14010050 - 10 Jan 2025

Abstract

The Lucas balancing polynomial is linked to a family of bi-starlike functions denoted as

S_{s c}^{c} (ϑ, Ξ (x))

, which we present and examine in this work. These functions are defined with respect to symmetric [...] Read more.

The Lucas balancing polynomial is linked to a family of bi-starlike functions denoted as

S_{s c}^{c} (ϑ, Ξ (x))

, which we present and examine in this work. These functions are defined with respect to symmetric conjugate points. Coefficient estimates are obtained for functions in this family. The classical Fekete–Szegö inequality of functions in this family is also obtained. Full article

(This article belongs to the Special Issue New Developments in Geometric Function Theory, 3rd Edition)

19 pages, 409 KiB

Open AccessArticle

On Equilibrium Problem for T-Shape Elastic Structure

by Alexander Khludnev

Axioms 2025, 14(1), 49; https://doi.org/10.3390/axioms14010049 - 10 Jan 2025

Abstract

This paper is concerned with an equilibrium problem for an elastic structure consisting of a plate and an elastic beam connected to each other at a given point. We consider two cases: In the first one, the elastic beam is connected to a [...] Read more.

This paper is concerned with an equilibrium problem for an elastic structure consisting of a plate and an elastic beam connected to each other at a given point. We consider two cases: In the first one, the elastic beam is connected to a rigid part of the elastic plate; in the second case, contact occurs between two elastic bodies. The elastic plate may contain a thin rigid delaminated inclusion. Neumann-type boundary conditions are considered at the external boundary of the plate. The existence of a solution to the considered problems is proven. A sufficient and necessary condition imposed onto the external forces for the solvability of the problems is found. Passages to the limit with respect to the rigidity parameter of the elastic beam are justified. For all problems, we analyze variational statements as well as differential ones. Full article

► Show Figures

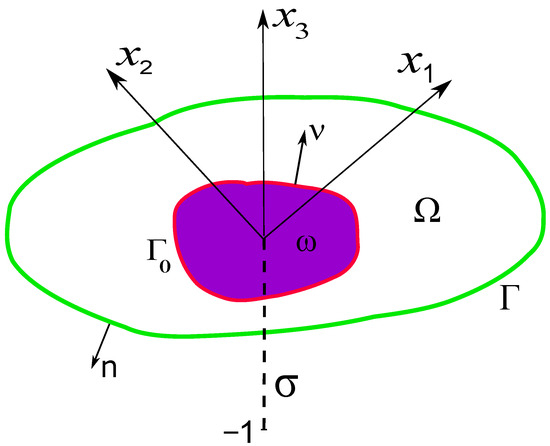
Figure 1

Journal Description

Axioms

Latest Articles

Journal Menu

Journal Browser

Highly Accessed Articles

Latest Books

E-Mail Alert

News

Topics

Conferences

Special Issues

Further Information

Guidelines

MDPI Initiatives

Follow MDPI