Cryptography

21 pages, 350 KiB

Open AccessReview

Elliptic Curve Cryptography with Machine Learning

by Jihane Jebrane, Akram Chhaybi, Saiida Lazaar and Abderrahmane Nitaj

Cryptography 2025, 9(1), 3; https://doi.org/10.3390/cryptography9010003 - 30 Dec 2024

Elliptic Curve Cryptography (ECC) is a technology based on the arithmetic of elliptic curves used to build strong and efficient cryptosystems and infrastructures. Several ECC systems, such as the Diffie–Hellman key exchange and the Elliptic Curve Digital Signature Algorithm, are deployed in real-life [...] Read more.

Elliptic Curve Cryptography (ECC) is a technology based on the arithmetic of elliptic curves used to build strong and efficient cryptosystems and infrastructures. Several ECC systems, such as the Diffie–Hellman key exchange and the Elliptic Curve Digital Signature Algorithm, are deployed in real-life applications to enhance the security and efficiency of digital transactions. ECC has gained even more importance since the introduction of Bitcoin, the peer-to-peer electronic cash system, by Satoshi Nakamoto in 2008. In parallel, the integration of artificial intelligence, particularly machine learning, in various applications has increased the demand for robust cryptographic systems to ensure safety and security. In this paper, we present an overview of machine learning and Elliptic Curve Cryptography algorithms. We begin with a detailed review of the main ECC systems and evaluate their efficiency and security. Subsequently, we investigate potential applications of machine learning-based techniques to enhance the security and performance of ECC. This study includes the generation of optimal parameters for ECC systems using machine learning algorithms. Full article

► Show Figures

Figure 1

18 pages, 302 KiB

Open AccessArticle

Partial Exposure Attacks Against a Family of RSA-like Cryptosystems

by George Teşeleanu

Cryptography 2025, 9(1), 2; https://doi.org/10.3390/cryptography9010002 - 28 Dec 2024

Abstract

An RSA generalization using complex integers was introduced by Elkamchouchi, Elshenawy and Shaban in 2002. This scheme was further extended by Cotan and Teșeleanu to Galois fields of order

n \geq 1

. In this generalized framework, the key equation is [...] Read more.

An RSA generalization using complex integers was introduced by Elkamchouchi, Elshenawy and Shaban in 2002. This scheme was further extended by Cotan and Teșeleanu to Galois fields of order

n \geq 1

. In this generalized framework, the key equation is

e d - k (p^{n} - 1) (q^{n} - 1) = 1

, where p and q are prime numbers. Note that the classical RSA and Elkamchouchi et al.’s key equations are special cases, namely, when

n = 1

and

n = 2

. In addition to introducing this generic family, Cotan and Teșeleanu described a continued fractions attack capable of recovering the secret key d if

d < N^{0.25 n}

. This bound was later improved by Teșeleanu using a lattice-based method. In this paper, we explore other lattice attacks that could lead to factoring the modulus

N = p q

, namely, we propose a series of partial exposure attacks that can aid an adversary in breaking this family of cryptosystems if certain conditions hold. Full article

18 pages, 525 KiB

Open AccessArticle

Security Proof of Single-Source Shortest Distance Protocols Built on Secure Multiparty Computation Protocols

by Mohammad Anagreh and Peeter Laud

Cryptography 2025, 9(1), 1; https://doi.org/10.3390/cryptography9010001 - 26 Dec 2024

Abstract

Secure secret-sharing Single-Source Shortest Distance (SSSD) protocols, based on secure multiparty computation (SMC), offer a promising solution for securely distributing and managing sensitive information among multiple parties. However, formal security proofs for these protocols have largely been unexplored. This paper addresses this gap [...] Read more.

Secure secret-sharing Single-Source Shortest Distance (SSSD) protocols, based on secure multiparty computation (SMC), offer a promising solution for securely distributing and managing sensitive information among multiple parties. However, formal security proofs for these protocols have largely been unexplored. This paper addresses this gap by providing the first security proof for the SSSD protocols using the privacy-preserving Bellman–Ford protocols. These new protocols offer significant enhancements in efficiency, particularly in handling large-scale graphs due to parallel computation. In our previous work, published in MDPI Cryptography, we introduced these protocols and presented extensive experiments on the Sharemind system that demonstrated their efficiency. However, that work did not include security proofs. Building on this foundation, the current paper rigorously proves the security of these protocols, offering valuable insights into their robustness and reliability. Furthermore, we discuss the adversarial model, security definitions, cryptographic assumptions, and sophisticated reduction techniques employed in the proof. This paper not only validates the security of the proposed protocols but also provides a detailed comparison of their performance with existing methods, highlighting their strengths and potential for future research in the field. Full article

(This article belongs to the Topic Recent Advances in Security, Privacy, and Trust)

► Show Figures

Figure 1

21 pages, 388 KiB

Open AccessArticle

Two-Party Threshold Private Set Intersection Protocols from Lightweight Cryptographic Primitives

by Shengnan Zhao, Chuan Zhao, Yuchen Huang, Xiangfu Song and Qiuliang Xu

Cryptography 2024, 8(4), 58; https://doi.org/10.3390/cryptography8040058 - 22 Dec 2024

Abstract

Private Set Intersection (PSI) is a significant application of interest within Secure Multi-party Computation (MPC), even though we are still in the early stages of deploying MPC solutions to real-world problems. Threshold PSI (tPSI), a variant of PSI, allows two parties to determine [...] Read more.

Private Set Intersection (PSI) is a significant application of interest within Secure Multi-party Computation (MPC), even though we are still in the early stages of deploying MPC solutions to real-world problems. Threshold PSI (tPSI), a variant of PSI, allows two parties to determine the intersection of their respective sets only if the cardinality of the intersection is at least (or less than) a specified threshold t. In this paper, we propose a generic construction for two-party tPSI that extensively utilizes Oblivious Transfer (OT). Our approach is based on lightweight primitives and avoids costly public-key systems such as homomorphic encryption. We start by introducing the secret-sharing private membership test

{}^{ss}{PMT}

that is based on the secret-sharing private equality test

{}^{ss}{PEQT}

. The

{}^{ss}{PMT}

enables tPSI to be scaled for a wide range of practical applications, particularly benefiting parties with limited computational resources. Consequently, two distinct two-party tPSI protocols can be efficiently implemented: over-threshold PSI (

t^{\leq} PSI

) and under-threshold PSI

t^{>} PSI

. In addition, we propose a lightweight two-party tPSI with limited leakage and a generic precomputing OT suitable for phased implementation. Experimental performance demonstrates that our protocols are highly efficient and computationally friendly, thus paving the way for broader deployment of tPSI solutions. Full article

► Show Figures

Figure 1

Figure 1
One-out-of-n Oblivious Transfer Functionality <math display="inline"><semantics> <msubsup> <mi mathvariant="script">F</mi> <mi>OT</mi> <mi mathvariant="normal">n</mi> </msubsup> </semantics></math>. Full article ">Figure 2
Private Equality Test <math display="inline"><semantics> <msub> <mi mathvariant="script">F</mi> <mi>PEQT</mi> </msub> </semantics></math>. Full article ">Figure 3
Secret-shared Private Equality Test <math display="inline"><semantics> <msubsup> <mi mathvariant="script">F</mi> <mi>PEQT</mi> <mrow> <mi>ss</mi> <mo>,</mo> <mi>q</mi> </mrow> </msubsup> </semantics></math>. Full article ">Figure 4
Private Membership Test <math display="inline"><semantics> <msub> <mi mathvariant="script">F</mi> <mi>PMT</mi> </msub> </semantics></math>. Full article ">Figure 5
Secret-shared Private Membership Test <math display="inline"><semantics> <msubsup> <mi mathvariant="script">F</mi> <mi>PMT</mi> <mrow> <mi>ss</mi> <mo>,</mo> <mi>q</mi> </mrow> </msubsup> </semantics></math>. Full article ">Figure 6
Secret-shared Private Membership Test Protocol <math display="inline"><semantics> <mmultiscripts> <mi>PMT</mi> <none/> <none/> <mprescripts/> <none/> <mi>ss</mi> </mmultiscripts> </semantics></math>. Full article ">Figure 7
Our <math display="inline"><semantics> <mmultiscripts> <mi>PEQT</mi> <none/> <none/> <mprescripts/> <none/> <mi>ss</mi> </mmultiscripts> </semantics></math> Construction Computing <math display="inline"><semantics> <msubsup> <mi mathvariant="script">F</mi> <mi>PEQT</mi> <mrow> <mi>ss</mi> <mo>,</mo> <mi>q</mi> </mrow> </msubsup> </semantics></math>. Full article ">Figure 8
Threshold Private Set Intersection tPSI. Full article ">Figure 9
Secure Comparison Functionality <math display="inline"><semantics> <msub> <mi mathvariant="script">F</mi> <mrow> <mo>≷</mo> <mo>(</mo> <msub> <mi>y</mi> <mn>0</mn> </msub> <mo>,</mo> <mi>x</mi> <mo>,</mo> <msub> <mi>y</mi> <mn>1</mn> </msub> <mo>)</mo> </mrow> </msub> </semantics></math>. Full article ">Figure 10
Threshold PSI <math display="inline"><semantics> <mrow> <msup> <mi>t</mi> <mstyle scriptlevel="2" displaystyle="false"> <mo>≤</mo> </mstyle> </msup> <mi>PSI</mi> </mrow> </semantics></math>. Full article ">Figure 11
Threshold PSI protocol with limited leakage (<math display="inline"><semantics> <mrow> <msubsup> <mi>t</mi> <mstyle scriptlevel="2" displaystyle="false"> <mrow> <mrow> <mi>l</mi> <mi>l</mi> </mrow> </mrow> </mstyle> <mstyle scriptlevel="2" displaystyle="false"> <mo>≤</mo> </mstyle> </msubsup> <mi>PSI</mi> </mrow> </semantics></math>). Full article ">Figure 12
Generic Precomputing <math display="inline"><semantics> <msubsup> <mi>OT</mi> <mi>n</mi> <mn>1</mn> </msubsup> </semantics></math> Method. Full article ">Figure 13
Running Time of <math display="inline"><semantics> <mmultiscripts> <mi>PEQT</mi> <none/> <none/> <mprescripts/> <none/> <mi>ss</mi> </mmultiscripts> </semantics></math>. Full article ">Figure 14
Comparisons of Running Time. Full article ">

20 pages, 356 KiB

Open AccessFeature PaperArticle

On the Proof of Ownership of Digital Wallets

by Chen Wang, Zi-Yuan Liu and Masahiro Mambo

Cryptography 2024, 8(4), 57; https://doi.org/10.3390/cryptography8040057 - 18 Dec 2024

Abstract

With the widespread adoption and increasing application of blockchain technology, cryptocurrency wallets used in Bitcoin and Ethereum play a crucial role in facilitating decentralized asset management and secure transactions. However, wallet security relies heavily on private keys, with insufficient attention to the risks [...] Read more.

With the widespread adoption and increasing application of blockchain technology, cryptocurrency wallets used in Bitcoin and Ethereum play a crucial role in facilitating decentralized asset management and secure transactions. However, wallet security relies heavily on private keys, with insufficient attention to the risks of theft and exposure. To address this issue, Chaum et al. (ACNS’21) proposed a “proof of ownership” method using a “backup key” to prove ownership of private keys even when exposed. However, their interactive proof approach is inefficient in large-scale systems and vulnerable to side-channel attacks due to the long key generation time. Other related schemes also suffer from low efficiency and complex key management, increasing the difficulty of securely storing backup keys. In this paper, we present an efficient, non-interactive proof generation approach for ownership of secret keys using a single backup key. Our approach leverages non-interactive zero-knowledge proofs and symmetric encryption, allowing users to generate multiple proofs with one fixed backup key, simplifying key management. Additionally, our scheme resists quantum attacks and provides a fallback signature. Our new scheme can be proved to capture unforgeability under the computational indistinguishability from the Uniformly Random Distribution property of a proper hash function and soundness in the quantum random oracle model. Experimental results indicate that our approach achieves a short key generation time and enables an efficient proof generation scheme in large-scale decentralized systems. Compared with state-of-the-art schemes, our approach is applicable to a broader range of scenarios due to its non-interactive nature, short key generation time, high efficiency, and simplified key management system. Full article

14 pages, 263 KiB

Open AccessArticle

A Matrix Multiplication Approach to Quantum-Safe Cryptographic Systems

by Luis Adrián Lizama-Pérez

Cryptography 2024, 8(4), 56; https://doi.org/10.3390/cryptography8040056 - 15 Dec 2024

Abstract

This paper introduces a novel approach based on matrix multiplication in

F_{p}^{n \times n}

, which enables methods for public key exchange, user authentication, digital signatures, blockchain integration, and homomorphic encryption. Unlike traditional algorithms that rely on integer factorization or discrete [...] Read more.

This paper introduces a novel approach based on matrix multiplication in

F_{p}^{n \times n}

, which enables methods for public key exchange, user authentication, digital signatures, blockchain integration, and homomorphic encryption. Unlike traditional algorithms that rely on integer factorization or discrete logarithms, our approach utilizes matrix factorization, rendering it resistant to current quantum cryptanalysis techniques. This method enhances confidentiality by ensuring secure communication and facilitating user authentication through public key validation. We have incorporated a method that allows a Certification Authority to certify the public keys. Furthermore, the incorporation of digital signatures ensures nonrepudiation, while the system functions as a blockchain technology to enhance transaction security. A key innovation of this approach is its capability to perform homomorphic encryption. Our approach has practical applications in artificial intelligence, robotics, and image processing. Full article

(This article belongs to the Special Issue Advances in Authentication, Authorization and Privacy for Securing Smart Communications)

► Show Figures

Figure 1

17 pages, 762 KiB

Open AccessArticle

Improving the Security of the LCB Block Cipher Against Deep Learning-Based Attacks

by Indrakanti Aishwarya, Lakshmy Koduvayur Viswanathan, Chungath Srinivasan, Girish Mishra, Saibal K. Pal and M. Sethumadhavan

Cryptography 2024, 8(4), 55; https://doi.org/10.3390/cryptography8040055 - 2 Dec 2024

Abstract

This study presents a robust version of Light Cipher Block (LCB) by addressing the vulnerabilities identified in previous versions. The vulnerabilities in LCB, including a linear S-Box, improper bit shuffling, and subkey reusability, were thoroughly examined. To overcome these weaknesses, a modified version [...] Read more.

This study presents a robust version of Light Cipher Block (LCB) by addressing the vulnerabilities identified in previous versions. The vulnerabilities in LCB, including a linear S-Box, improper bit shuffling, and subkey reusability, were thoroughly examined. To overcome these weaknesses, a modified version called Secure LCB is introduced, incorporating changes to the P-Box and key generation algorithm. Motivated by Gohr’s work at CRYPTO’19, this paper investigates the use of a neural distinguisher built upon a 1-dimensional convolutional neural network (1-d CNN). The deep learning model is tasked with identifying ciphertexts that have a specific, controlled difference in their inputs, as opposed to those with random input differences. The evaluation of the proposed Secure LCB using the neural distinguisher suggests that the modifications made to LCB have effectively enhanced its resistance against the neural distinguisher’s classification. This highlights the importance of addressing vulnerabilities in cryptographic systems and showcases the potential of machine learning techniques in cryptanalysis. Full article

► Show Figures

Figure 1

17 pages, 338 KiB

Open AccessArticle

New Weak Keys with Parity Patterns in the RC4 Stream Cipher

by Evaristo José Madarro-Capó, Carlos Miguel Legón-Pérez , Guillermo Sosa-Gómez and Omar Rojas

Cryptography 2024, 8(4), 54; https://doi.org/10.3390/cryptography8040054 - 27 Nov 2024

Abstract

The RC4 cryptographic algorithm is the most extensively studied stream cipher of the past two decades. This extensive research has resulted in numerous publications, many of which identify various vulnerabilities. Although these vulnerabilities do not preclude the correct use of the algorithm, they [...] Read more.

The RC4 cryptographic algorithm is the most extensively studied stream cipher of the past two decades. This extensive research has resulted in numerous publications, many of which identify various vulnerabilities. Although these vulnerabilities do not preclude the correct use of the algorithm, they complicate its practical implementation. In this paper, we present a novel weakness in the RC4 cipher. Our findings indicate that, for input keys exhibiting certain patterns, the parity of the values in the output permutation of the KSA can be determined with high probability from the parity of its position in the output permutation. Furthermore, the use of keys with these specific patterns leads to noticeable distortions in several bytes of the RC4 output. Full article

(This article belongs to the Special Issue Advances in Symmetric Cryptography and Data Integrity)

► Show Figures

Figure 1

17 pages, 749 KiB

Open AccessFeature PaperArticle

Implantable Medical Device Security

by Luigi Catuogno and Clemente Galdi

Cryptography 2024, 8(4), 53; https://doi.org/10.3390/cryptography8040053 - 15 Nov 2024

Abstract

Implantable medical devices, or IMDs for short, are medical instruments that are placed into the human body through surgery. IMDs are typically used for treating chronic diseases. Currently available IMDs are capable of communicating using wireless channels with other devices, either in close [...] Read more.

Implantable medical devices, or IMDs for short, are medical instruments that are placed into the human body through surgery. IMDs are typically used for treating chronic diseases. Currently available IMDs are capable of communicating using wireless channels with other devices, either in close proximity or even connected to the Internet, making IMDs part of the Internet of Medical Things. This capability opens the possibility of developing a wide range of services, like remote patient data control, localization in case of emergency, or telemedicine, which can improve patients’ lifestyle. On the other hand, given the limited resources of such tiny devices, and the access to the Internet, there are numerous security issues to be considered when designing and deploying IMDs and their support infrastructures. In this paper, we highlight security problems related to Internet-connected IMDs, and survey some solutions that have been presented in the literature. Full article

(This article belongs to the Special Issue Emerging Topics in Hardware Security)

► Show Figures

Figure 1

18 pages, 678 KiB

Open AccessArticle

An Anonymous Authenticated Key Agreement Scheme for Telecare Medical Information Systems

by Ghassan Hameed Faraj, Kamal Shahtalebi and Hamid Mala

Cryptography 2024, 8(4), 52; https://doi.org/10.3390/cryptography8040052 - 13 Nov 2024

Abstract

With the rapid development of information technology from one side and the experience of the COVID-19 pandemic from the other side, people presently prefer to access healthcare services remotely. Telecare Medical Information System (TMIS) provides more flexible, faster, and more convenient e-healthcare services [...] Read more.

With the rapid development of information technology from one side and the experience of the COVID-19 pandemic from the other side, people presently prefer to access healthcare services remotely. Telecare Medical Information System (TMIS) provides more flexible, faster, and more convenient e-healthcare services available to all people, particularly those who lack access to physicians due to their geographical restrictions. However, due to the sensitivity of medical information, preventing unauthorized access to patient data and preserving patient privacy is crucial. In this paper, we propose an authenticated key agreement scheme for TMIS to preserve the privacy of the patient’s identity from all internal (even the health server and the physician) and external entities. Moreover, the physician’s identity is kept secret from all external entities. Formal and informal security analysis of the proposed scheme indicates that it is secure against all attacks in the context. Full article

► Show Figures

Figure 1

30 pages, 1096 KiB

Open AccessFeature PaperArticle

A Secure Approach Out-of-Band for e-Bank with Visual Two-Factor Authorization Protocol

by Laerte Peotta de Melo, Dino Macedo Amaral, Robson de Oliveira Albuquerque, Rafael Timóteo de Sousa Júnior, Ana Lucila Sandoval Orozco and Luis Javier García Villalba

Cryptography 2024, 8(4), 51; https://doi.org/10.3390/cryptography8040051 - 11 Nov 2024

Abstract

The article presents an innovative approach for secure authentication in internet banking transactions, utilizing an Out-of-Band visual two-factor authorization protocol. With the increasing rise of cyber attacks and fraud, new security models are needed that ensure the integrity, authenticity, and confidentiality of financial [...] Read more.

The article presents an innovative approach for secure authentication in internet banking transactions, utilizing an Out-of-Band visual two-factor authorization protocol. With the increasing rise of cyber attacks and fraud, new security models are needed that ensure the integrity, authenticity, and confidentiality of financial transactions. The identified gap lies in the inability of traditional authentication methods, such as TANs and tokens, to provide security in untrusted terminals. The proposed solution is the Dynamic Authorization Protocol (DAP), which uses mobile devices to validate transactions through visual codes, such as QR codes. Each transaction is assigned a unique associated code, and the challenge must be responded to within 120 s. The customer initiates the transaction on a computer and independently validates it on their mobile device using an out-of-band channel to prevent attacks such as phishing and man-in-the-middle. The methodology involves implementing a prototype in Java ME for Android devices and a Java application server, creating a practical, low-computational-cost system, accessible for use across different operating systems and devices. The protocol was tested in real-world scenarios, focusing on ensuring transaction integrity and authenticity. The results show a successful implementation at Banco do Brasil, with 3.6 million active users, demonstrating the efficiency of the model over 12 years of use without significant vulnerabilities. The DAP protocol provides a robust and effective solution for securing banking transactions and can be extended to other authentication environments, such as payment terminals and point of sale devices. Full article

► Show Figures

Figure 1

46 pages, 707 KiB

Open AccessFeature PaperArticle

Quantum Security of a Compact Multi-Signature

by Shaoquan Jiang

Cryptography 2024, 8(4), 50; https://doi.org/10.3390/cryptography8040050 - 28 Oct 2024

Abstract

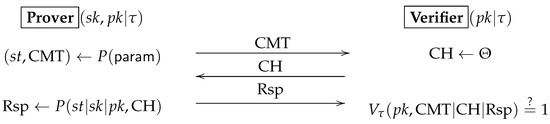
With the rapid advances in quantum computing, quantum security is now an indispensable property for any cryptographic system. In this paper, we study how to prove the security of a complex cryptographic system in the quantum random oracle model. We first give a [...] Read more.

With the rapid advances in quantum computing, quantum security is now an indispensable property for any cryptographic system. In this paper, we study how to prove the security of a complex cryptographic system in the quantum random oracle model. We first give a variant of Zhandry’s compressed random oracle (CStO), called a compressed quantum random oracle with adaptive special points (CStO_s). Then, we extend the on-line extraction technique of Don et al. (EUROCRYPT’22) from CStO to

{CStO}_{s}

. We also extend the random experiment technique of Liu and Zhandry (CRYPTO’19) for extracting the

CStO

query that witnesses the future adversarial output. With these preparations, a systematic security proof in the quantum random oracle model can start with a random CStO experiment (that extracts the witness for the future adversarial output) and then converts this game to one involving

{CStO}_{s}

. Next, the online extraction technique for

{CStO}_{s}

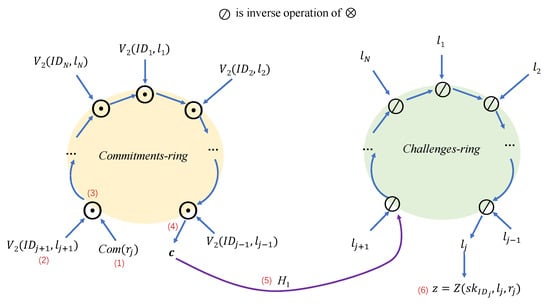
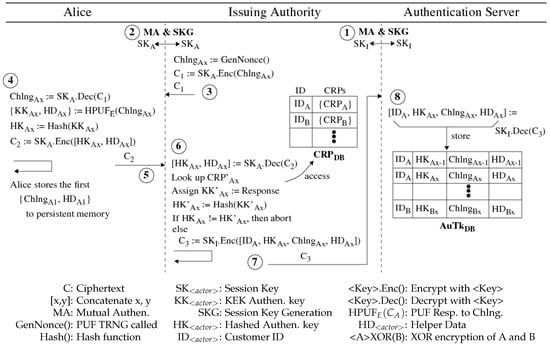
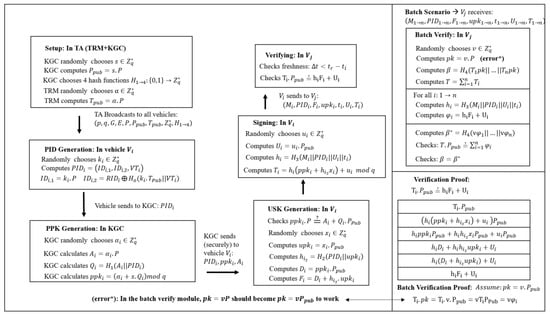
can be applied to extract the witness for any online commitment. With this strategy, we give a security proof of our recent compact multi-signature framework that is converted from any weakly secure linear ID scheme. We also prove the quantum security of our recent lattice realization of this linear ID scheme by iteratively applying the weakly collapsing protocol technique of Liu and Zhandry (CRYPTO 2019). Combining these two results, we obtain the first quantum security proof for a compact multi-signature. Full article

► Show Figures

Figure 1

18 pages, 3123 KiB

Open AccessArticle

Design and Performance Evaluation of an Authentic End-to-End Communication Model on Large-Scale Hybrid IPv4-IPv6 Virtual Networks to Detect MITM Attacks

by Zeeshan Ashraf, Adnan Sohail and Muddesar Iqbal

Cryptography 2024, 8(4), 49; https://doi.org/10.3390/cryptography8040049 - 28 Oct 2024

Abstract

After the end of IPv4 addresses, the Internet is moving towards IPv6 address architecture quickly with the support of virtualization techniques worldwide. IPv4 and IPv6 protocols will co-exist long during the changeover process. Some attacks, such as MITM attacks, do not discriminate by [...] Read more.

After the end of IPv4 addresses, the Internet is moving towards IPv6 address architecture quickly with the support of virtualization techniques worldwide. IPv4 and IPv6 protocols will co-exist long during the changeover process. Some attacks, such as MITM attacks, do not discriminate by appearance and affect IPv4 and IPv6 address architectures. In an MITM attack, the attacker secretly captures the data, masquerades as the original sender, and sends it toward the receiver. The receiver replies to the attacker because the receiver does not authenticate the source. Therefore, the authentication between two parties is compromised due to an MITM attack. The existing authentication schemes adopt complicated mathematical procedures. Therefore, the existing schemes increase computation and communication costs. This paper proposes a lightweight and authentic end-to-end communication model to detect MITM attacks using a pre-shared symmetric key. In addition, we implement and analyze the performance of our proposed security model on Linux-based virtual machines connected to large-scale hybrid IPv4-IPv6 virtual networks. Moreover, security analyses prove the effectiveness of our proposed model. Finally, we compare the performance of our proposed security model with existing models in terms of computation cost and communication overhead. Full article

► Show Figures

Figure 1

19 pages, 755 KiB

Open AccessArticle

Post-Quantum Secure ID-Based (Threshold) Linkable Dual-Ring Signature and Its Application in Blockchain Transactions

by Wen Gao, Haoyuan Yao, Baodong Qin, Xiaoli Dong, Zhen Zhao and Jiayu Zeng

Cryptography 2024, 8(4), 48; https://doi.org/10.3390/cryptography8040048 - 28 Oct 2024

Abstract

Ring signatures are widely used in e-voting, anonymous whistle-blowing systems, and blockchain transactions. However, due to the anonymity of ring signatures, a signer can sign the same message multiple times, potentially leading to repeated voting or double spending in blockchain transactions. To address [...] Read more.

Ring signatures are widely used in e-voting, anonymous whistle-blowing systems, and blockchain transactions. However, due to the anonymity of ring signatures, a signer can sign the same message multiple times, potentially leading to repeated voting or double spending in blockchain transactions. To address these issues in blockchain transactions, this work constructs an identity-based linkable ring signature scheme based on the hardness of the lattice-based Module Small Integer Solution (M-SIS) assumption, which is hard even for quantum attackers. The proposed scheme is proven to be anonymous, unforgeable, linkable, and nonslanderable in the random oracle model. Compared to existing identity-based linkable ring signature (IBLRS) schemes of linear size, our signature size is relatively smaller, and this advantage is more pronounced when the number of ring members is small. We provide approximate signature size data for ring members ranging from 2 to 2048. When the number of ring members is 16 (or 512. resp.), the signature size of our scheme is 11.40 KB (or 24.68 KB, respectively). Finally, a threshold extension is given as an additional scheme with specifications and security analysis. Full article

► Show Figures

Figure 1

20 pages, 2973 KiB

Open AccessArticle

Next-Generation Block Ciphers: Achieving Superior Memory Efficiency and Cryptographic Robustness for IoT Devices

by Saadia Aziz, Ijaz Ali Shoukat, Mohsin Iftikhar, Mohsin Murtaza, Abdulmajeed M. Alenezi, Cheng-Chi Lee and Imran Taj

Cryptography 2024, 8(4), 47; https://doi.org/10.3390/cryptography8040047 - 23 Oct 2024

Abstract

Traditional cryptographic methods often need complex designs that require substantial memory and battery power, rendering them unsuitable for small handheld devices. As the prevalence of these devices continues to rise, there is a pressing need to develop smart, memory-efficient cryptographic protocols that provide [...] Read more.

Traditional cryptographic methods often need complex designs that require substantial memory and battery power, rendering them unsuitable for small handheld devices. As the prevalence of these devices continues to rise, there is a pressing need to develop smart, memory-efficient cryptographic protocols that provide both high speed and robust security. Current solutions, primarily dependent on dynamic permutations, fall short in terms of encryption and decryption speeds, the cryptographic strength, and the memory efficiency. Consequently, the evolution of lightweight cryptographic algorithms incorporating randomised substitution properties is imperative to meet the stringent security demands of handheld devices effectively. In this paper, we present an advanced design of lightweight block ciphers that enhances traditional dynamic permutations with innovative randomised substitutions. This design utilises straightforward randomized encryption methods such as XOR, nibble swap, count ones, and left shift. The cryptographic robustness of our proposed block cipher has been rigorously tested through several standardised statistical tests, as recommended by the National Institute of Standards and Technology (NIST). These evaluations confirm that our algorithm maintains strong cryptographic properties with randomised substitutions and outperforms existing models in several key aspects. Moreover, comparative assessments reveal that our algorithm achieves a throughput of 853.31 Kbps while consuming only 1510 bytes of memory and demonstrating over 60% avalanche properties, significantly outperforming other solutions in terms of CPU utilisation and memory consumption. These results underscore the efficacy of our approach in fulfilling the advanced security requirements of modern handheld devices. Full article

(This article belongs to the Special Issue Advances in Authentication, Authorization and Privacy for Securing Smart Communications)

► Show Figures

Figure 1

22 pages, 1342 KiB

Open AccessArticle

Lightweight Mutually Authenticated Key Exchange with Physical Unclonable Functions

by Cyrus Minwalla, Jim Plusquellic and Eirini Eleni Tsiropoulou

Cryptography 2024, 8(4), 46; https://doi.org/10.3390/cryptography8040046 - 19 Oct 2024

Abstract

Authenticated key exchange is desired in scenarios where two participants must exchange sensitive information over an untrusted channel but do not trust each other at the outset of the exchange. As a unique hardware-based random oracle, physical unclonable functions (PUFs) can embed cryptographic [...] Read more.

Authenticated key exchange is desired in scenarios where two participants must exchange sensitive information over an untrusted channel but do not trust each other at the outset of the exchange. As a unique hardware-based random oracle, physical unclonable functions (PUFs) can embed cryptographic hardness and binding properties needed for a secure, interactive authentication system. In this paper, we propose a lightweight protocol, termed PUF-MAKE, to achieve bilateral mutual authentication between two untrusted parties with the help of a trusted server and secure physical devices. At the end of the protocol, both parties are authenticated and possess a shared session key that they can use to encrypt sensitive information over an untrusted channel. The PUF’s underlying entropy hardness characteristics and the key-encryption-key (KEK) primitive act as the root of trust in the protocol’s construction. Other salient properties include a lightweight construction with minimal information stored on each device, a key refresh mechanism to ensure a fresh key is used for every authentication, and robustness against a wide range of attacks. We evaluate the protocol on a set of three FPGAs and a desktop server, with the computational complexity calculated as a function of primitive operations. A composable security model is proposed and analyzed considering a powerful adversary in control of all communications channels. In particular, session key confidentiality is proven through formal verification of the protocol under strong attacker (Dolev-Yao) assumptions, rendering it viable for high-security applications such as digital currency. Full article

(This article belongs to the Section Hardware Security)

► Show Figures

Figure 1

Figure 1
Message exchange diagram for PUF-MAKE Enrollment. Full article ">Figure 2
Message exchange diagram for in-field authentication between Alice and Bob. The strike-outs, indicated with red lines in the <math display="inline"><semantics> <mrow> <mi>A</mi> <mi>u</mi> <mi>T</mi> <msub> <mi>k</mi> <mrow> <mi>D</mi> <mi>B</mi> </mrow> </msub> </mrow> </semantics></math>, identify used AT that are deleted from the database. Full article ">Figure 3
A formally verified model of in-field authentication. Full article ">Figure 4
Established queries for formal verification. Full article ">Figure 5
Entropy and MinEntropy of 10,000 <math display="inline"><semantics> <msub> <mi>KK</mi> <mi>A</mi> </msub> </semantics></math> that are generated over a 4.5 h run of the MAKE protocol. Full article ">Figure 6
Intra-chip Hamming Distance statistics for 10,000 KK from Alice and Bob’s devices (superimposed curves), produced in one minute time intervals over a 4.5 h duration. Full article ">Figure 7
Transaction times of PUF-MAKE In-Field protocol steps: (1) <math display="inline"><semantics> <msub> <mi>SK</mi> <mi>T</mi> </msub> </semantics></math> generation; (2) <math display="inline"><semantics> <msub> <mi>KK</mi> <mi>A</mi> </msub> </semantics></math> generation and hash to <math display="inline"><semantics> <msub> <mi>HK</mi> <mi>A</mi> </msub> </semantics></math>; (3) <math display="inline"><semantics> <msub> <mi mathvariant="normal">C</mi> <mn>1</mn> </msub> </semantics></math>, <math display="inline"><semantics> <msub> <mi mathvariant="normal">C</mi> <mn>2</mn> </msub> </semantics></math> creation and transmission to AS; (4) DB search, <math display="inline"><semantics> <msub> <mi mathvariant="normal">C</mi> <mi>A</mi> </msub> </semantics></math>, <math display="inline"><semantics> <msub> <mi mathvariant="normal">C</mi> <mi>B</mi> </msub> </semantics></math> creation and transmission from AS; (5) <math display="inline"><semantics> <msub> <mi mathvariant="normal">C</mi> <mi>A</mi> </msub> </semantics></math>, <math display="inline"><semantics> <msub> <mi mathvariant="normal">C</mi> <mi>B</mi> </msub> </semantics></math> extraction and SK creation; (6) Encrypt-transmit-decrypt test message with SK; and (7) total authentication time. Full article ">

10 pages, 232 KiB

Open AccessArticle

Combined and General Methodologies of Key Space Partition for the Cryptanalysis of Block Ciphers

by Mijail Borges-Quintana, Miguel A. Borges-Trenard, Osmani Tito-Corrioso, Omar Rojas and Guillermo Sosa-Gómez

Cryptography 2024, 8(4), 45; https://doi.org/10.3390/cryptography8040045 - 11 Oct 2024

Abstract

This paper proposes two new methods of key space partitioning for the cryptanalysis of block ciphers. The first one is called combined methodology of key space partition (CoMeKSPar), which allows us to simultaneously set some of the first and last consecutive bits of [...] Read more.

This paper proposes two new methods of key space partitioning for the cryptanalysis of block ciphers. The first one is called combined methodology of key space partition (CoMeKSPar), which allows us to simultaneously set some of the first and last consecutive bits of the key. In this way, the search is performed using the remaining middle bits. CoMeKSPar is a combination of two methods already proposed in the scientific literature, the Borges, Borges, Monier (BBM) and the Tito, Borges, Borges (TBB). The second method is called the general algorithm of key space reduction (GAKSRed), which makes it possible to perform a genetic algorithm search in the space formed by the unknown bits of the key, regardless of their distribution in the binary block. Furthermore, a method of attacking block ciphers is presented for the case where some key bits are known; the basic idea is to deduce some of the remaining bits of the block. An advantage of these methods is that they allow parallel computing, which allows simultaneous searches in different sub-blocks of key bits, thereby increasing the probability of success. The experiments are performed with the KLEIN (Small) lightweight block cipher using the genetic algorithm. Full article

(This article belongs to the Topic Recent Advances in Security, Privacy, and Trust)

16 pages, 318 KiB

Open AccessArticle

Partial Exposure Attacks on a New RSA Variant

by Mohammed Rahmani, Abderrahmane Nitaj and Mhammed Ziane

Cryptography 2024, 8(4), 44; https://doi.org/10.3390/cryptography8040044 - 6 Oct 2024

Abstract

In 2022, Cotan and Teşeleanu presented a variant of the RSA cryptosystem where the modulus is of the form

N = p q

, and the private and the public exponents satisfy [...] Read more.

In 2022, Cotan and Teşeleanu presented a variant of the RSA cryptosystem where the modulus is of the form

N = p q

, and the private and the public exponents satisfy

e d \equiv 1 (mod ψ_{n} (N))

with

n \geq 2

, and

ψ_{n} (N) = \frac{(p^{n} - 1) (q^{n} - 1)}{(p - 1) (q - 1)}

. This variant of RSA was recently cryptanalyzed by Nitaj, Adenan, and Ariffin at Africacrypt 2024. In this paper, we push further the cryptanalysis of the scheme of Cotan and Teşeleanu by presenting a method to solve the equation

x H (y) + c \equiv 0 (mod e)

where c is a constant that is independent of x and y. This enables us to propose more attacks on the scheme, including a partial key exposure attack, an attack when the most significant bits of one of the prime factors are known, and an attack when the least significant bits of one of the prime factors are known. Full article

16 pages, 1860 KiB

Open AccessArticle

CHAM-CLAS: A Certificateless Aggregate Signature Scheme with Chameleon Hashing-Based Identity Authentication for VANETs

by Ahmad Kabil, Heba Aslan, Marianne A. Azer and Mohamed Rasslan

Cryptography 2024, 8(3), 43; https://doi.org/10.3390/cryptography8030043 - 17 Sep 2024

Abstract

Vehicular ad hoc networks (VANETs), which are the backbone of intelligent transportation systems (ITSs), facilitate critical data exchanges between vehicles. This necessitates secure transmission, which requires guarantees of message availability, integrity, source authenticity, and user privacy. Moreover, the traceability of network participants is [...] Read more.

Vehicular ad hoc networks (VANETs), which are the backbone of intelligent transportation systems (ITSs), facilitate critical data exchanges between vehicles. This necessitates secure transmission, which requires guarantees of message availability, integrity, source authenticity, and user privacy. Moreover, the traceability of network participants is essential as it deters malicious actors and allows lawful authorities to identify message senders for accountability. This introduces a challenge: balancing privacy with traceability. Conditional privacy-preserving authentication (CPPA) schemes are designed to mitigate this conflict. CPPA schemes utilize cryptographic protocols, including certificate-based schemes, group signatures, identity-based schemes, and certificateless schemes. Due to the critical time constraints in VANETs, efficient batch verification techniques are crucial. Combining certificateless schemes with batch verification leads to certificateless aggregate signature (CLAS) schemes. In this paper, cryptanalysis of Xiong’s CLAS scheme revealed its vulnerabilities to partial key replacement and identity replacement attacks, alongside mathematical errors in the batch verification process. Our proposed CLAS scheme remedies these issues by incorporating an identity authentication module that leverages chameleon hashing within elliptic curve cryptography (CHAM-CLAS). The signature and verification modules are also redesigned to address the identified vulnerabilities in Xiong’s scheme. Additionally, we implemented the small exponents test within the batch verification module to achieve Type III security. While this enhances security, it introduces a slight performance trade-off. Our scheme has been subjected to formal security and performance analyses to ensure robustness. Full article

► Show Figures

Figure 1

Journal Description

Cryptography

Latest Articles

Journal Menu

Journal Browser

Highly Accessed Articles

Latest Books

E-Mail Alert

News

Topics

Conferences

Special Issues

Topical Collections

Further Information

Guidelines

MDPI Initiatives

Follow MDPI